Tài liệu Bài giải phần giải mạch P5 pptx
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (1.84 MB, 51 trang )
Chapter 5, Solution 1.
(a) R
in
= 1.5 MΩ
(b) R
out
= 60 Ω
(c) A = 8x10
4
Therefore A
dB
= 20 log 8x10
4
= 98.0 dB
Chapter 5, Solution 2.
v
0
= Av
d
= A(v
2
- v
1
)
= 10
5
(20-10) x 10
-6
= 0.1V
Chapter 5, Solution 3.
v
0
= Av
d
= A(v
2
- v
1
)
= 2 x 10
5
(30 + 20) x 10
-6
= 10V
Chapter 5, Solution 4.
v
0
= Av
d
= A(v
2
- v
1
)
v
2
- v
1
= V20
10x2
4
A
v
5
0
µ−=
−
=
If v
1
and v
2
are in mV, then
v
2
- v
1
= -20 mV = 0.02
1 - v
1
= -0.02
v
1
= 1.02 mV
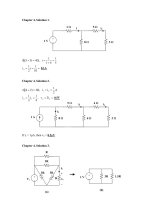
Chapter 5, Solution 5.
+
v
0
-
-
v
d
+
R
0
R
in
I
v
i
-
+
Av
d
+
-
-v
i
+ Av
d
+ (R
i
- R
0
) I = 0 (1)
But v
d
= R
i
I,
-v
i
+ (R
i
+ R
0
+ R
i
A) I = 0
v
d
=
i0
ii
R)A1(R
Rv
++
(2)
-Av
d
- R
0
I + v
0
= 0
v
0
= Av
d
+ R
0
I = (R
0
+ R
i
A)I =
i0
ii0
R)A1(R
v)ARR(
++
+
4
5
54
i0
i0
i
0
10
)101(100
10x10100
R)A1(R
ARR
v
v
⋅
++
+
=
++
+
=
≅
()
=⋅
+
4
5
9
10
101
10
=
001,100
000,100
0.9999990
Chapter 5, Solution 6.
-
v
d
+
+
v
o
-
R
0
R
in
I
v
i
+
-
Av
d
+
-
(R
0
+ R
i
)R + v
i
+ Av
d
= 0
But v
d
= R
i
I,
v
i
+ (R
0
+ R
i
+ R
i
A)I = 0
I =
i0
i
R)A1(R
v
++
−
(1)
-Av
d
- R
0
I + v
o
= 0
v
o
= Av
d
+ R
0
I = (R
0
+ R
i
A)I
Substituting for I in (1),
v
0
=
++
+
i0
i0
R)A1(R
ARR
−
v
i
=
()
()
65
356
10x2x10x2150
1010x2x10x250
++
⋅+
−
−
≅
mV
10x2x001,200
10x2x000,200
6
6
−
v
0
= -0.999995 mV
Chapter 5, Solution 7.
100 k
Ω
1
2
10 kΩ
-
+
+
V
d
-
+
V
out
-
R
out
= 100 Ω
R
in
AV
d
+
-
V
S
At node 1, (V
S
– V
1
)/10 k = [V
1
/100 k] + [(V
1
– V
0
)/100 k]
10
V
S
– 10 V
1
= V
1
+ V
1
– V
0
which leads to V
1
= (10V
S
+ V
0
)/12
At node 2, (V
1
– V
0
)/100 k = (V
0
– AV
d
)/100
But V
d
= V
1
and A = 100,000,
V
1
– V
0
= 1000 (V
0
– 100,000V
1
)
0= 1001V
0
– 100,000,001[(10V
S
+ V
0
)/12]
0 = -83,333,334.17 V
S
- 8,332,333.42 V
0
which gives us (V
0
/ V
S
) = -10 (for all practical purposes)
If V
S
= 1 mV, then V
0
= -10 mV
Since V
0
= A V
d
= 100,000 V
d
, then V
d
= (V
0
/10
5
) V = -100 nV
Chapter 5, Solution 8.
(a) If v
a
and v
b
are the voltages at the inverting and noninverting terminals of the op
amp.
v
a
= v
b
= 0
1mA =
k2
v0
0
−
v
0
= -2V
(b)
10 kΩ
2V
+ -
+
v
a
-
10 kΩ
i
a
+
v
o
-
+
v
o
-
v
a
v
b
i
a
2 k
Ω
2V
-
+
1V
-
+
-
+
(b)
(a)
Since v
a
= v
b
= 1V and i
a
= 0, no current flows through the 10 kΩ resistor. From Fig. (b),
-v
a
+ 2 + v
0
= 0 v
a
= v
a
- 2 = 1 - 2 = -1V
Chapter 5, Solution 9.
(a) Let v
a
and v
b
be respectively the voltages at the inverting and noninverting
terminals of the op amp
v
a
= v
b
= 4V
At the inverting terminal,
1mA =
k2
0
v4
−
v
0
= 2V
Since v
a
= v
b
= 3V,
-v
b
+ 1 + v
o
= 0 v
o
= v
b
- 1 = 2V
+
v
b
-
+
v
o
-
+ -
(b)
1V
Chapter 5, Solution 10.
Since no current enters the op amp, the voltage at the input of the op amp is v
s
.
Hence
v
s
= v
o
2
v
1010
10
o
=
+
s
o
v
v
= 2
Chapter 5, Solution 11.
8
k
Ω
v
b
= V2)3(
510
10
=
+
i
o
b
a
+
−
5
k
Ω
2
k
Ω
4
k
Ω
+
v
o
−
10
k
Ω
−
+
3 V
At node a,
8
vv
2
v3
oaa
−
=
−
12 = 5v
a
– v
o
But v
a
= v
b
= 2V,
12 = 10 – v
o
v
o
= -2V
–i
o
=
mA1
4
2
8
22
4
v0
8
vv
ooa
=+
+
=
−
+
−
i
o
= -1mA
Chapter 5, Solution 12.
4
k
Ω
b
a
+
−
2
k
Ω
1
k
Ω
+
v
o
−
4
k
Ω
−
+
1.2V
At node b, v
b
=
ooo
v
3
2
v
3
2
v
24
4
==
+
At node a,
4
vv
1
v2.1
oaa
−
=
−
, but v
a
= v
b
=
o
v
3
2
4.8 - 4 x
ooo
vv
3
2
v
3
2
−= v
o
= V0570.2
7
8.4x3
=
v
a
= v
b
=
7
6.9
v
3
2
o
=
i
s
=
7
2.1
1
v2.
a
−
=
1
−
p = v
s
i
s
= 1.2 =
−
7
2.1
-205.7 mW
Chapter 5, Solution 13.
By voltage division,
i
1
i
2
90
k
Ω
10
k
Ω
b
a
+
−
100 k
Ω
4
k
Ω
50
k
Ω
+
−
i
o
+
v
o
−
1 V
v
a
=
V9.0)1(
100
=
90
v
b
=
3
v
v
150
o
o
=
50
But v
a
= v
b
9.0
3
v
0
= v
o
= 2.7V
i
o
= i
1
+ i
2
= =+
k150
v
k10
v
oo
0.27mA + 0.018mA = 288 µA
Chapter 5, Solution 14.
Transform the current source as shown below. At node 1,
10
vv
20
vv
5
v10
o1
211
−
+
−
=
−
But v
2
= 0. Hence 40 - 4v
1
= v
1
+ 2v
1
- 2v
o
40 = 7v
1
- 2v
o
(1)
20
k
Ω
v
o
10
k
Ω
+
−
v
1
−
+
v
2
5
k
Ω
10
k
Ω
+
v
o
−
10V
At node 2,
0v,
10
vv
20
vv
2
o2
21
=
−
=
−
or v
1
= -2v
o
(2)
From (1) and (2), 40 = -14v
o
- 2v
o
v
o
= -2.5V
Chapter 5, Solution 15
(a) Let v
1
be the voltage at the node where the three resistors meet. Applying
KCL at this node gives
332
1
3
1
2
1
11
R
v
RR
v
R
vv
R
v
i
oo
s
−
+=
−
+=
(1)
At the inverting terminal,
11
1
1
0
Riv
R
v
i
ss
−=→
−
=
(2)
Combining (1) and (2) leads to
++−=→−=
++
2
31
31
33
1
2
1
1
R
RR
RR
i
v
R
v
R
R
R
R
i
s
oo
s
(b)
For this case,
Ω=Ω
++−= k 92- k
25
4020
4020
x
i
v
s
o
Chapter 5, Solution 16
10k
Ω
i
x
5k
Ω
v
a
i
y
-
v
b
+ v
o
+ 2k
Ω
0.5V
- 8k
Ω
Let currents be in mA and resistances be in k
Ω
. At node a,
oa
oaa
vv
vvv
−=→
−
=
−
31
105
5.0
(1)
But
aooba
vvvvv
8
10
28
8
=→
+
== (2)
Substituting (2) into (1) gives
14
8
8
10
31
=→−=
aaa
vvv
Thus,
A 28.14mA 70/1
5
5.0
µ
−=−=
−
=
a
x
v
i
A 85.71mA
14
8
4
6.0
)
8
10
(6.0)(6.0
102
µ
==−=−=
−
+
−
= xvvvv
vvvv
i
aaao
aobo
y
Chapter 5, Solution 17.
(a) G = =−=−=
5
12
R
R
v
v
1
2
i
o
-2.4
(b)
5
80
v
v
i
o
−= = -16
(c)
=−=
5
2000
v
v
i
o
-400
Chapter 5, Solution 18.
Converting the voltage source to current source and back to a voltage source, we have the
circuit shown below:
3
20
2010
= kΩ
1 M
Ω
3
v2
3
20
50
1000
v
i
o
⋅
+
−= =−=
17
200
v
1
o
v
-11.764
Chapter 5, Solution 19.
We convert the current source and back to a voltage source.
3
4
42
=
5
k
Ω
v
o
0V
(
4/3
)
k
Ω 10
k
Ω
−
+
4
k
Ω
+
−
(2/3)V
(
20/3
)
k
Ω
+
v
o
−
−
+
50
k
Ω
+
−
2v
i
/3
=
−=
3
2
k
3
4
x4
k10
v
o
-1.25V
=
−
+=
k
10
0v
k
5
v
i
oo
o
-0.375mA
Chapter 5, Solution 20.
8
k
Ω
+
−
v
s
+
−
4
k
Ω
+
v
o
−
−
+
2
k
Ω
4
k
Ω
a b
9 V
At node a,
4
vv
8
vv
4
v9
baoaa
−
+
−
=
−
18 = 5v
a
– v
o
- 2v
b
(1)
At node b,
2
vv
4
vv
obba
−
=
−
v
a
= 3v
b
- 2v
o
(2)
But v
b
= v
s
= 0; (2) becomes v
a
= –2v
o
and (1) becomes
-18 = -10v
o
– v
o
v
o
= -18/(11) = -1.6364V
Chapter 5, Solution 21.
Eqs. (1) and (2) remain the same. When v
b
= v
s
= 3V, eq. (2) becomes
v
a
= 3 x 3 - 2v
0
= 9 - 2v
o
Substituting this into (1), 18 = 5 (9-2v
o
) – v
o
– 6 leads to
v
o
= 21/(11) = 1.909V
Chapter 5, Solution 22.
A
v
= -R
f
/R
i
= -15.
If R
i
= 10kΩ, then R
f
= 150 kΩ.
Chapter 5, Solution 23
At the inverting terminal, v=0 so that KCL gives
121
0
0
0
R
R
v
v
R
v
RR
v
f
s
o
f
os
−=→
−
+=
−
Chapter 5, Solution 24
v
1
R
f
R
1
R
2
- v
s
+ -
+
+
R
4
R
3
v
o
v
2
-
We notice that v
1
= v
2
. Applying KCL at node 1 gives
f
os
ff
os
R
v
R
v
v
RRRR
vv
R
vv
R
v
=−
++→=
−
+
−
+
2
1
21
1
2
1
1
1
111
0
)(
(1)
Applying KCL at node 2 gives
s
s
v
RR
R
v
R
vv
R
v
43
3
1
4
1
3
1
0
+
=→=
−
+ (2)
Substituting (2) into (1) yields
s
f
fo
v
RRR
R
R
R
R
R
R
R
Rv
−
+
−+=
243
3
2
4
3
1
3
1
i.e.
−
+
−+=
243
3
2
4
3
1
3
1
RRR
R
R
R
R
R
R
R
Rk
f
f
Chapter 5, Solution 25.
v
o
= 2 V
+ −
+
v
a
+
v
o
-v
a
+ 3 + v
o
= 0 which leads to v
a
= v
o
+ 3 = 5 V.
Chapter 5, Solution 26
+
v
b
- i
o
+ +
0.4V 5k
Ω
- 2k
Ω
v
o
8k
Ω
-
V 5.08.0/4.08.0
28
8
4.0 ==→=
+
==
ooob
vvvv
Hence,
mA 1.0
5
5.0
5
===
kk
v
o
o
i
Chapter 5, Solution 27.
(a) Let v
a
be the voltage at the noninverting terminal.
v
a
= 2/(8+2) v
i
= 0.2v
i
ia0
v2.10v
20
1 =
+
1000
v
=
G = v
0
/(v
i
) = 10.2
(b) v
i
= v
0
/(G) = 15/(10.2) cos 120πt = 1.471 cos 120πt V
Chapter 5, Solution 28.
−
+
+
−
At node 1,
k
50
vv
k
10
v0
o1
1
−
=
−
But v
1
= 0.4V,
-5v
1
= v
1
– v
o
, leads to v
o
= 6v
1
= 2.4V
Alternatively, viewed as a noninverting amplifier,
v
o
= (1 + (50/10)) (0.4V) = 2.4V
i
o
= v
o
/(20k) = 2.4/(20k) = 120 µA
Chapter 5, Solution 29
R
1
v
a
+
v
b
- +
+
v
i
R
2
R
2
v
o
- R
1
-
obia
v
RR
R
vv
RR
R
v
21
1
21
2
,
+
=
+
=
But
oiba
v
RR
R
v
RR
R
v
21
1
21
2
+
=
+
→=
v
Or
1
2
R
R
v
v
i
o
=
Chapter 5, Solution 30.
The output of the voltage becomes
v
o
= v
i
= 12
Ω= k122030
By voltage division,
V2.0)2.1(
6012
12
v
x
=
+
=
===
k20
2.0
k20
v
i
x
x
10µA
===
k
20
04.0
R
v
p
2
x
2µW
Chapter 5, Solution 31.
After converting the current source to a voltage source, the circuit is as shown below:
12
k
Ω
2
v
o
6
k
Ω
+
−
+
−
6
k
Ω
3
k
Ω
1
v
1
v
o
12 V
At node 1,
12
vv
6
vv
3
v
o1o1
1
12
−
+
−
=
−
48 = 7v
1
- 3v
o
(1)
At node 2,
x
oo1
i
6
0v
6
vv
=
−
=
−
v
1
= 2v
o
(2)
From (1) and (2),
11
48
v
o
=
==
k
6
v
i
o
x
0.7272mA
Chapter 5, Solution 32.
Let v
x
= the voltage at the output of the op amp. The given circuit is a non-inverting
amplifier.
=
x
v
+
10
50
1 (4 mV) = 24 mV
Ω= k203060
By voltage division,
v
o
= mV12
2
v
v
2020
o
o
==
+
20
i
x
=
()
==
+ k40
mV24
k2020
v
x
600nA
p =
=
−
3
6
2
o
10x60
10x
=
144
R
v
204nW
Chapter 5, Solution 33.
After transforming the current source, the current is as shown below:
1
k
Ω
This is a noninverting amplifier.
3
k
Ω
v
i
v
a
+
−
+
−
2
k
Ω
4
k
Ω
v
o
4 V
iio
v
2
3
v
2
1
1v =
+=
Since the current entering the op amp is 0, the source resistor has a OV potential drop.
Hence v
i
= 4V.
V6)4(
2
3
v
o
==
Power dissipated by the 3kΩ resistor is
==
k
3
36
R
v
2
o
12mW
=
−
=
−
=
k
1
64
R
vv
i
oa
x
-2mA
Chapter 5, Solution 34
0
R
vv
R
vv
2
in1
1
in1
=
−
+
−
(1)
but
o
43
3
a
v
RR
R
v
+
= (2)
Combining (1) and (2),
0v
R
R
v
R
R
vv
a
2
1
2
2
1
a1
=−+−
2
2
1
1
2
1
a
v
R
R
v
R
R
1v +=
+
2
2
1
1
2
1
43
o3
v
R
R
v
R
R
1
RR
vR
+=
+
+
+
+
+
=
2
2
1
1
2
1
3
43
o
v
R
R
v
R
R
1R
RR
v
v
O
= )vRv(
)RR(R
RR
221
213
43
+
+
+
Chapter 5, Solution 35.
10
R
R
1
v
v
A
i
f
i
o
v
=+== R
f
= 9R
i
If R
i
= 10kΩ, R
f
= 90kΩ
Chapter 5, Solution 36
V
abTh
V=
But
abs
V
RR
R
21
1
+
=
v
. Thus,
ssabTh
v
R
R
v
R
RR
VV )1(
1
2
1
21
+=
+
==
To get R
Th
, apply a current source I
o
at terminals a-b as shown below.
v
1
+
v
2
- a
+
R
2
v
o
i
o
R
1
-
b
Since the noninverting terminal is connected to ground, v
1
= v
2
=0, i.e. no current passes
through R
1
and consequently R
2
. Thus, v
o
=0 and
0==
o
o
Th
i
v
R
Chapter 5, Solution 37.
++−=
3
3
f
2
2
f
1
1
f
o
v
R
R
v
R
R
v
R
R
v
−++−= )3(
30
30
)2(
20
30
)1(
10
30
v
o
= -3V
Chapter 5, Solution 38.
+++−=
4
4
f
3
3
f
2
2
f
1
1
f
o
v
R
R
v
R
R
v
R
R
v
R
R
v
−++−+−= )100(
50
50
)50(
10
50
)20(
20
50
)10(
25
50
=
-120mV
Chapter 5, Solution 39
This is a summing amplifier.
223
3
2
2
1
1
5.29)1(
50
50
20
50
)2(
10
50
vvv
R
R
v
R
R
v
R
R
v
fff
o
−−=
−++−=
++−=
Thus,
V 35.295.16
22
=→−−=−= vvv
o
Chapter 5, Solution 40
R
1
R
2
v
a
+
R
3
v
b -
+ +
v
1
+
- v
2
R
f
v
o
- +
v
3
R -
-
Applying KCL at node a,
)
111
(0
3213
3
2
2
1
1
3
3
2
2
1
1
RRR
v
R
v
R
v
R
v
R
vv
R
vv
R
vv
a
aaa
++=++→=
−
+
−
+
−
(1)
But
o
f
ba
v
RR
R
v
+
==v
(2)
Substituting (2) into (1)gives
)
111
(
3213
3
2
2
1
1
RRRRR
Rv
R
v
R
v
R
v
f
o
++
+
=++
or
)
111
/()(
3213
3
2
2
1
1
RRRR
v
R
v
R
v
R
RR
v
f
o
++++
+
=
Chapter 5, Solution 41.
R
f
/R
i
= 1/(4) R
i
= 4R
f
= 40kΩ
The averaging amplifier is as shown below:
Chapter 5, Solution 42
v
1
R
2
= 40
k
Ω
v
2
R
3
= 40
k
Ω
v
3
R
4
= 40
k
Ω
v
4
10
k
Ω
−
+
R
1
= 40
k
Ω
v
o
Ω== k 10R
3
1
R
1f
Chapter 5, Solution 43.
In order for
+++=
4
4
f
3
3
f
2
2
f
1
1
f
o
v
R
R
v
R
R
v
R
R
v
R
R
v
to become
()
4321o
vvvv
4
1
v +++−=
4
1
R
R
i
f
= ===
4
12
4
R
R
i
f
3kΩ
Chapter 5, Solution 44.
R
4
At node b,
0
R
vv
R
vv
2
2b
1
1b
=
−
+
−
21
2
2
1
1
b
R
1
R
1
R
v
R
v
v
+
+
= (1)
b
a
R
1
v
1
R
2
v
2
R
3
v
o
−
+
At node a,
4
oa
3
a
R
vv
R
v0 −
=
−
34
o
a
R/R1
v
v
+
= (2)
But v
a
= v
b
. We set (1) and (2) equal.
21
1112
34
o
RR
vRvR
R/R1
v
+
+
=
+
or
v
o
=
()
()
()
1112
213
43
vRvR
RRR
RR
+
+
+
Chapter 5, Solution 45.
This can be achieved as follows:
()
+−−=
21o
v
2/R
R
v
3/R
R
v
()
+−−=
2
2
f
1
1
f
v
R
R
v
R
R
i.e. R
f
= R, R
1
= R/3, and R
2
= R/2
Thus we need an inverter to invert v
1
, and a summer, as shown below (R<100kΩ).
R/3
R/2
v
2
R
−
+
R
v
1
-v
1
R
−
+
v
o
Chapter 5, Solution 46.
3
3
f
2
2
x
1
1
f
32
1
o
v
R
R
)v(
R
R
v
R
R
v
2
1
)v(
3
1
3
v
v +−+=+−+=−
i.e. R
3
= 2R
f
, R
1
= R
2
= 3R
f
. To get -v
2
, we need an inverter with R
f
= R
i
. If R
f
= 10kΩ,
a solution is given below.
v
1
30
k
Ω
20
k
Ω
v
3
10
k
Ω
−
+
10
k
Ω
v
2
-v
2
10
k
Ω
−
+
30
k
Ω
v
o
Chapter 5, Solution 47.
If a is the inverting terminal at the op amp and b is the noninverting terminal,
then,
V6vv,V6)8(
13
3
v
bab
===
+
= and at node a,
4
vv
2
v10
oaa
−
=
−
which leads to v
o
= –2 V and i
o
=
k4
)vv(
k5
v
oao
−
− = –0.4 – 2 mA = –2.4 mA
Chapter 5, Solution 48.
Since the op amp draws no current from the bridge, the bridge may be treated separately
as follows:
v
1
v
2
i
2
i
1
+
−
For loop 1, (10 + 30) i
1
= 5 i
1
= 5/(40) = 0.125µA
For loop 2, (40 + 60) i
2
= -5 i
2
= -0.05µA
But, 10i + v
1
- 5 = 0 v
1
= 5 - 10i = 3.75mV
60i + v
2
+ 5 = 0 v
2
= -5 - 60i = -2mV
As a difference amplifier,
()
[]
mV)2(75.3
20
80
vv
R
R
v
12
1
2
o
−−=−=
=
23mV
Chapter 5, Solution 49.
R
1
= R
3
= 10kΩ, R
2
/(R
1
) = 2
i.e. R
2
= 2R
1
= 20kΩ = R
4
Verify:
1
1
2
2
43
21
1
2
o
v
R
R
v
R/R1
R/R1
R
R
v −
+
+
=
()
1212
vv2v2v
5.01
)5.01(
2 −=−
+
+
=
Thus, R
1
= R
3
= 10kΩ, R
2
= R
4
= 20kΩ
Chapter 5, Solution 50.
(a) We use a difference amplifier, as shown below:
()(
,vv2vv
R
R
v
1212
1
2
o
−=−=
)
i.e. R
2
/R
1
= 2
R
1
v
2
R
2
v
1
R
2
−
+
R
1
v
o
If R
1
= 10 kΩ then R
2
= 20kΩ
(b)
We may apply the idea in Prob. 5.35.
210
v2v2v −=
()
+−−=
21
v
2/R
R
v
2/R
R
()
+−−=
2
2
f
1
1
f
v
R
R
v
R
R
i.e. R
f
= R, R
1
= R/2 = R
2