CÁC DẠNG TOÁN VỀ TỔ HỢP - XÁC SUẤT
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (1.55 MB, 21 trang )
1
CHỦ ĐỀ 6: MỘT SỐ DẠNG TOÁN VỀ TỔ HỢP VÀ XÁC SUẤT
(Dành cho 11K2 ôn tập trong hè)
Phần I: Một số bài toán tổ hợp
Phương pháp:
Ta áp dụng quy tắc cộng, quy tắc nhân và các công thức sau
! 1 2 3 3.2.1
n
P n n n n n
!
!
k
n
n
A
nk
!
!!
k
n
n
C
k n k
.
Dạng 1: Chọ
n một nhóm phần tử từ tập hợp
Ví dụ 1: Một hộ
p đựng 11 tấm thẻ được đánh số từ 1 đến 11. Hỏi có bao nhiêu cách lấy ra 6 thẻ
để
tổng số ghi trên 6 thẻ đó là một số lẻ.
Giải
Ta kí hiệu: thẻ ghi số lẻ là thẻ lẻ; thẻ ghi số chẵn là thẻ chẵn.
Tổng số ghi trên 6 thẻ lấy ra là một số lẻ thì số thẻ lẻ lấy ra phải là một số lẻ . Ta có các trường
hợp (TH) sau:
TH1: 1 thẻ lẻ, 5 thẻ chẵn suy ra có
15
65
6CC
cách.
TH2: 3 thẻ lẻ, 3 thẻ chẵn suy ra có
33
65
200CC
cách.
TH3: 5 thẻ lẻ, 1 thẻ chẵn suy ra có
51
65
30CC
cách.
Vậy có:
6 200 30 236
cách.
Ví dụ 2: Trong số 16 học sinh có
3
học sinh giỏi, 5 khá và 8 trung bình. Hỏi có bao nhiêu cách
chia 16 học sinh đó thành 2 tổ, mỗi tổ 8 người sao cho mỗi tổ đều có học sinh giỏi và mỗi tổ có
ít nhất hai học sinh khá.
Giải
2
Ta có bảng phân chia các trường hợp sau :
Trường
hợp
HS giỏi
(3)
HS khá
(5)
HS trung bình
8
Số cách chọn
1
1
2
5
1 2 5
3 5 8
1680C C C
2
1
3
4
1 3 4
3 5 8
2100C C C
3
2
2
4
224
3 5 8
2100CCC
4
2
3
3
2 3 3
3 5 8
1680C C C
Kết quả
7560
Vậy có : 7560 cách .
Bài tập
1. Một đội thanh niên xung kích có 12 học sinh gồm 5 học sinh lớp A, 4 học sinh của lớp B,
3 học sinh của lớp C. Cần chọn 4 học sinh đi làm nhiệm vụ, sao cho mỗi lớp có ít nhất 1
học sinh. Hỏi có bao nhiêu cách chọn. Đáp số :
270
cách.
2. Thầy giáo có 30 câu hỏi khác nhau gồm 5 câu khó, 10 câu trung bình, 15 câu dễ. Từ 30
câu hỏi trên lập được bao nhiêu đề kiểm tra, mỗi đề 5 câu hỏi khác nhau, sao cho trong
mỗi đề phải đủ 3 loại câu ( khó, trung bình, dễ) và số câu hỏi dễ không ít hơn 2.
Đáp số:
56875
.
3. Một đội thanh niên tình nguyện có 15 người, gồm 12 nam và 3 nữ. Hỏi có bao nhiêu
cách phân công đội thanh niên tình nguyện đó về giúp đỡ 3 tỉnh miền núi sao cho mỗi
tỉnh có 4 nam và 1 nữ . Đáp số :
207900
cách.
Dạng 2: Sắp xếp thứ tự các phần tử từ các tập hợp
Ví dụ : Một nhóm học sinh gồm 7 nam và 3 nữ. Hỏi có bao nhiêu cách xếp 10 em học sinh này
thành một hàng ngang sao cho:
a) Giữa hai học sinh nữ bất kì đều không có một em nam nào.
b) Hai vị trí đầu và cuối hàng là các em nam và không có hai em nữ nào ngồi cạnh nhau.
Giải
a) Ta xem 3 em nữ là một vị trí trong hàng . Như vậy 7 em nam và khối 3 em nữ tạo thành 8
vị trí trên hàng:
3
Xếp chỗ cho 7 em nam và khối 3 em nữ có :
8!
cách.
Xếp chỗ trong nội bộ khối 3 em nữ có :
3!
cách.
Vậy có :
8!.3! 241920
cách.
b) Xếp chỗ cho 7 em nam có
7!
cách.
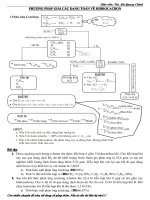
Xếp chỗ cho 3 em nữ theo yêu cầu , giữa hai nữ bất kì phải có một em nam.
1
B
2
B
3
B
4
B
5
B
6
B
7
B
1
G
2
G
3
G
4
G
5
G
6
G
i
G
là vị trí giữa học sinh nam
i
B
và
1i
B
,
1,6i
. Khi đó vị trí của của 3 em nữ là chỉnh
hợp chập 3 của 6 phần tử , do đó có
3
6
A
cách xếp vị trí cho 3 em nữ.
Vậy có:
3
6
7!. 604800A
cách xếp chỗ thõa mãn đề bài.
Bài tập
1. Cho tập hợp
1;2;3;4;5A
. Từ tập hợp A lập được bao nhiêu số
a) Có 6 chữ số sao cho trong mỗi số số 1 xuất hiện 2 lần, còn các số khác xuất hiện đúng
một lần. Đáp số:
360
số.
b) Có 7 chữ số sao cho trong mỗi số đó số 1 xuất hiện hai lần, số 2 xuất hiện 3 lần còn các
số khác xuất hiện không quá một lần. Đáp số:
1260
số.
2. Cho tập hợp
2;5A
. Hỏi có thể lập được bao nhiêu số cps 10 chữ số sao cho không có
hai chữ số 2 nào đứng cạnh nhau. Đáp số :
144
số.
3. Cho tập hợp các chữ số
0;1; 2; 3; 4; 5
. Từ chúng viết được bao nhiêu số tự nhiên gồm
5
chữ số mà trong đó có hai chữ số
1
và ba chữ số còn lại khác nhau và khác
1
?
Hướng dẫn:
TH1: Trong số tạo thành có chữ số
0
: Số số là
22
44
4. . 288CA
.
TH2: Trong số tạo thành không có chữ số
0
: Số số là
23
54
. 240CA
.
Đáp số:
528
số.
4. Có bao nhiêu cách chia
6
người ra thành
3
nhóm, mỗi nhóm
2
người, trong mỗi trường
hợp sau:
a. Phân biệt thứ tự các nhóm là: nhóm
1
, nhóm
2
, nhóm
3
.
b. Không phân biệt thứ tự của các nhóm ?
Đáp số: a.
222
6 4 2
. . 90CCC
b.
222
6 4 2
15
3!
CCC
5. Từ các chữ số 0,1,2,3,4 có thể lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau?
Tính tổng của các số tự nhiên đó. Đáp số:96 số và có tổng là 2599980.
Phần II: Một số bài toán về nhị thức Newton
Bài tập: Giải các phương trình, bất phương trình sau
4
Phần này ta xét các dạng toán trọng tâm như: tính tổng, chứng minh đẳng thức, giải phương
trình, bất phương trình,hệ phương trình và tìm hệ số của đa thức trong khai triển Newton.
Dạng 1: Giải phương trình, bất phương trình, hệp phương trình tổ hợp.
Phương pháp:
Bước 1: Đặt điều kiện cho ẩn số
Bươc 2: Sử dụng các công thức về hoán vị, chỉnh hợp tổ hơp để biến đổi, rút gọn giải
phương trình,bất phương trình ,hệ phương trình.
Bước 3: kết hợp nghiệm vừa tìm được với điều kiện ban đầu để tìm nghiệm của bài toán.
Ví dụ 1: Giải bất phương trình
2 2 3
2
16
10
2
x x x
A A C
x
1
Giải
Điều kiện:
3,x x N
1
2!
1 ! 6 ! 1
. 10 1 2 1 1 2 10
2 2 2 ! 2 ! 3! 3 ! 2
x
xx
x x x x x x
x x x x
4x
. Do
3,x x Z
nên
3; 4.xx
Ví dụ 2: Giải hệ phương trình
2 5 90
2 5 80
yy
xx
yy
xx
AC
AC
Giải
Điều
*
,,x y N x y
Hệ phương trình
!
20
!
20
!
20
1 20
!
!
2
10
10
!2
!!
y
x
y
x
x
x
xy
A
xx
xy
x
y
C
y
y x y
5, 4 5
22
x x x
yy
.
Vậy nghiệm của hệ phương trình đã cho là:
5; 2xy
.
5
1.
3 1 3 2
1 1 6
2 3 3 159
xx
x x x
A C C x P
. Đáp số :
12x
.
2.
22
72 6 2
x x x x
P A A P
. Đáp số:
3; 4xx
.
3.
3
1
4
13
1
14
n
n
n
C
AP
. Đáp số:
6,nn
.
Dạng 2: Tính tổng
Phương pháp:
Ta sử dụng một số công thức sau
k n k
nn
CC
11
1
k k k
n n n
C C C
0 1 2
2
nn
n n n n
C C C C
0 2 4 2 1 3 5 2 1 2 1
2 2 2 2 2 2 2 2
2
n n n
n n n n n n n n
C C C C C C C C
.
Ngoài ra ta còn kết hợp giữa khai triển Newton, đạo hàm và tích phân để tính tổng.
Ví dụ 1: Tính tổng sau
1 3 5 2 1
4 4 4 4
n
n n n n
S C C C C
Giải
Ta có
k n k
nn
CC
4 1 4 3 4 5 2 1
4 4 4 4
n n n n
n n n n
S C C C C
1 3 5 4 1
4 4 4 4
2
n
n n n n
S C C C C
Xét khai triển
4 0 1 2 2 3 3 4 1 4 1 4 4
4 4 4 4 4 4
(1 )
n n n n n
n n n n n n
x C C x C x C x C x C x
Chọn
1x
, ta có :
0 1 2 3 4 1 4
4 4 4 4 4 4
0
nn
n n n n n n
C C C C C C
1
Chọn
1x
, ta có :
0 1 2 3 4 1 4 4
4 4 4 4 4 4
2
n n n
n n n n n n
C C C C C C
2
Trừ vế theo vế của
2
cho
1
ta được:
1 3 5 4 1 4 1
4 4 4 4
2
nn
n n n n
C C C C
4 1 4 2
2 2 2
nn
SS
.
Vậy
42
2
n
S
.
Ví dụ 2: Tính tổng sau
0 1 2 2013
2013 2013 2013 2013
2 3 2014S C C C C
6
Giải
Xét khai triển
2013
0 1 2 2 2013 2013
2013 2013 2013 2013
1 x C C x C x C x
1
Chọn
1x
, ta có :
0 1 2 2013 2013
1 2013 2013 2013 2013
2S C C C C
Đạo hàm hai vế của
1
ta có :
2012
1 2 2013 2012
2013 2013 2013
2013 1 2 2013x C C x C x
Chọn
1x
, ta có :
1 2 2013 2012
2 2013 2013 2013
2 2013 2013.2S C C C
Ta có :
0 1 2 2012 2013
2 2013 2013 2013 2013 2013 3
S S C C C C C S
2012 2013 2012
23
2013.2 2 2015.2S S S
.
Vậy
2012
2015.2S
.
Ví dụ 3: Tính tổng sau
2 2 3 3 1 1
0 1 2
2 3 1
nn
n
n n n n
b a b a b a
S b a C C C C
n
Với
*
nN
,
ba
.
Giải
Ta có:
0 1 2 2 0 1 2 2
1 1
bb
nn
n n n n
n n n n n n n n
aa
x C C x C x C x x dx C C x C x C x dx
11
2 2 3 3 1 1
0 1 2
11
2 3 1 1
nn
nn
n
n n n n
ba
b a b a b a
b a C C C C
nn
.
Vậy
11
11
1
nn
ba
S
n
.
Bài tập: Tính các tổng sau
1.
6 7 8 9 10 11
11 11 11 11 11 11
S C C C C C C
HD:
0 1 3 9 10 11 11 10
11 11 11 11 11 11
2 2 2S C C C C C C S
.
2.
0 1 2
2 3 1 1
n
n
n n n n
S C C C n C
HD:
1
n
P x x x
, đạo hàm
' 1 0SP
.
Giải
7
3.
0 1 2
1 1 1
2 3 1
n
n n n n
S C C C C
n
HD:
1
1
0
21
1
1
n
n
S x dx
n
Dạng 3 : Chứng minh đẳng thức
Phương pháp:
Sử dụng :Tính chất của các hệ số trong khai triển Newton hoặc dùng khai triển Newton kết hợp
với đạo hàm tích phân để chứng minh.
Ví dụ 1: Chứng minh rằng
0 2 2 4 4 2 2 1 2
2 2 2 2
3 3 2 2 1
n n n
n n n n
C C C C
1
Giải
Xét khai triển :
2
0 1 2 2 3 3 2 2
2 2 2 2 2
1
n
nn
n n n n n
x C C x C x C x C x
Chọn
3x
, ta có :
2 0 1 2 2 2 2
2 2 2 2
4 3 3 3
n n n
n n n n
C C C C
2
Chọn
3x
, ta có :
2 0 1 2 2 2 2
2 2 2 2
2 3 3 3
n n n
n n n n
C C C C
3
Cộng vế theo vế của
2
và
3
ta có:
2 2 0 2 2 4 4 2
2 2 2 2
4 2 2 3 3
n n n
n n n n
C C C C
0 2 2 4 4 2 2 1 2
2 2 2 2
3 3 2 2 1
n n n
n n n n
C C C C
điều phải chứng minh.
Ví dụ 2: Chứng minh rằng
1 1 2 2 3 3 1
3 2 3 3 3 .4
n n n n n
n n n n
C C C nC n
2
Giải
Xét khai triển :
0 1 1 2 2 2 3 3 3
2
3 3 3 3 3
n
n n n n n n
n n n n n
x C C x C x C x C x
Đạo hàm hai vế :
1
1 1 2 2 3 3 2 1
3 3 2 3 3 3
n
n n n n n
n n n n
n x C C x C x nC x
Chọn
1 1 2 2 3 3 1
1 3 2 3 3 3 .4
n n n n n
n n n n
x C C C nC n
điều phải chứng minh.
Ví dụ 3: Chứng minh rằng
0 1 2 3
1
1
2 4 6 8 2 2 2 1
n
n
n
n n n n
C
C C C C
nn
3
8
Xét khai triển :
2 0 1 2 2 2 2 2
1 ( ) ( ) ( )
n
nn
n n n n
x C C x C x C x
2 0 3 1 5 2 2 1
1 1
n
nn
n n n n
x x xC x C x C x C
1
22
1
2 4 6
2 0 1 2
0
0
1
1
2 4 6 2 2
n
n
n
n
n n n n
x
x x x
I x x dx C C C C
n
0 1 2 3
1
1
2 4 6 8 2 2 2 1
n
n
n
n n n n
C
C C C C
nn
điều phải chứng minh.
Bài tập: Chứng minh các đẳng thức sau
1.
2 2 2 2
0 1 2
2
nn
n n n n n
C C C C C
HD: Ta có
0 1 1 0 1
1 1
nn
n n n n n
n n n n n n
x x C x C x C C C x C x
hệ số của
n
x
; Tìm hệ số
n
x
trong khai triển
2
1
n
x
suy ra điều phải chứng minh.
2.
1 2 3
3
33
k k k k k
n n n n n
C C C C C
với
,kn
và
3 kn
.
3.
0 2 2 4 4 2012 2012 2012 2013
2013 2013 2013 2013
3 3 3 2 2 1C C C C
HD: Khai triển
2013 2013
1 ; 1xx
, cộng vế theo vế và chọn
3x
.
4.
1 1 1 2 3 3 1
2 2 3.2 .3
n n n n n
n n n n
C C C nC n
HD: Khai triển
1
n
x
, đạo hàm , chọn
1
2
x
.
Dạng 4 : Tính hệ số của đa thức
4.1: Tính hệ số của số hạng
m
x
trong khai triển nhị thức Newton của
n
P x f x
Phương pháp:
Bước 1: Viết
0
n
gk
k
k
P x a x
Bước 2: Số hạng chứa
m
x
tương ứng với
g k m
k
.
Bước 3: Kết luận
Nếu
,k N k n
, thì hệ số phải tìm là
k
a
.
Nếu
kn
hoặc
kn
thì trong khia triển không có số hạng
m
x
, hệ số phải tìm bằng
0.
9
Ví dụ 1: Tìm số hạng không chứa x trong khai triển
28
3
15
n
x x x
, biết rằng
12
79
n n n
n n n
C C C
.
Giải
Điều kiện :
2,n n N
Ta có :
1 2 2
12
1
79 1 79 156 0 12
13
2
n n n
n n n
n
nn
C C C n n n n
n
Suy ra :
12
28 4 28 48 112
12
3
15 3 15 15 5
12
0
n
k
k
k
x x x x x C x
Số hạng không chứa x là
0
x
48 112
07
15 5
k
k
.
Số hạng không chứa x là số hạng thứ 8, có hệ số là
7
12
792C
.
Ví dụ 2: Tìm hệ số của
4
x
trong khai triển thành đa thức của biểu thức
10
2
1 2 3P x x x
Giải
Ta có :
10 10 10
10
10
2 2 2
10 10 10
0 0 0
1 2 3 1 2 3 2 3
k
k
ki
k k i k k
k
k k i
P x x x C x x C C x x
10 10
2
10 10
00
23
k
k i i k k i
k
ki
C C x
, theo bài ra ta có hệ :
24
, , 10, 10
ki
i k N k i k
0
4
k
i
;
1
2
k
i
;
2
0
k
i
. Vậy hệ số của
4
x
trong khai triển trên là :
0 4 0 4 1 2 1 2 2 0 2 0
10 10 10 9 10 8
3 2 3 2 3 2 8085C C C C C C
.
Ví dụ 3
10
Cho đa thức
2 3 20
1 2 1 3 1 20 1P x x x x x
. Tìm hệ số của số hạng x
15
trong khai triển thành đa thức của
Px
.
Giải
Viết lại :
Px
2 14
1 2 1 14 1x x x
+
15 16 20
15 16 20
0 0 0
15 16 20
k k k k k k
k k k
C x C x C x
Suy ra hệ số của số hạng chứa x
15
là :
15 15 15 15 15 15
15 15 16 17 18 19 20
15 16 17 18 19 20 400995a C C C C C C
.
Bài tập:
1. Tìm số hạng không chứa x trong khai triển
7
5
1
2x
x
. Đáp số: 6528.
2. Tìm hệ số của số hạng chứa x
8
trong khai triển nhị thức Newton
5
3
1
n
x
x
biết rằng:
1
43
7( 3)
nn
nn
C C n
. Đáp số:
4
12
495C
.
3. Tìm hệ số của x
5
trong khai triển của biểu thức: P=
5 10
2
1 2 1 3x x x x
.Đáp số:
3320
.
4. Tìm hệ số của x
8
trong khai triển thành đa thức
8
2
11P x x x
. Đáp số :
238
5. Cho biết
0 1 1 2 2 3 3
3 3 3 3 1 2048.
n
n n n n n
n n n n n
C C C C C
Tìm hệ số của
10
x
trong
khai triển nhị thức
2.
n
x
Đáp số:
11
11
11, 2 22.nC
6. Cho biết
1 2 20
2 1 2 1 2 1
2 1.
n
n n n
C C C
Tìm hệ số của
26
x
trong khai triển nhị thức
Newton của
7
4
1
.
n
x
x
Đáp số:
4
10
10, 210.nC
4.1: Tính hệ số lớn nhất trong khai triển nhị thức Newton của
ax
m
b
Phương pháp:
11
Bước 1: Tìm hệ số
n
a
nm
của số hạng tổng quát.
Bước 2: Giải bất phương trình
1nn
aa
, suy ra
1nn
aa
với ẩn số n.
Bước 3: Hệ số có giá trị lớn nhất tương ứng với số tự nhiên lớn nhất thỏa mãn bất
phương trình trên.
Ví dụ 1 ( Đề thi tuyển sinh Đại học khối A -2008)
Giả sử
2
0 1 2
n
n
P x a a x a x a x
thỏa mãn hệ thức:
12
12
0
2
2
2 2 2
n
n
a
aa
a
.
Tìm hệ số lớn nhất trong các hệ số
0 1 2
; ; ; ;
n
a a a a
Giải
Theo công thức khai triển nhị thức Newton ta có:
0 1 2 2 2
0
1 2 2 2 2 2
n
n
k k k n n n
n n n n n
x
k
P x C x C C x C x C x
Từ đó do
Px
12
n
x
=
2
0 1 2
n
n
a a x a x a x
, ta có:
0
0 n
aC
11
1
1
2
2
nn
a
a C C
2 2 2
2
2
2
2
2
nn
a
a C C
…………
2
2
n n n
n
n n n
n
a
a C C
Vì thế:
01
12
0
2
2
2 2 2
nn
n
n n n
n
a
aa
a C C C
.
Do đó từ giả thiết suy ra:
12
2 2 12
n
n
.
12
Xét khai triển:
12
12
12
0
1 2 2
k k k
k
x C x
. Từ đó
12
2
kk
k
aC
(k
0, 1, 2,…,12)
Xét bất phương trình:
1kk
aa
11
12 12
12! 12! 1 2
2 2 2 2 1 24 2
12 ! ! 11 ! 1 ! 12 1
k k k k
C C k k
k k k k k k
23
0,1,2, ,7
3
kk
(do k nguyên)
Từ đó suy ra :
1kk
aa
23
8,9,10,11
3
kk
Phương trình
1kk
aa
23
3
k
vô nghiệm do k nguyên
Như thế ta có
0 1 2 7 8 9 10 11 12
a a a a a a a a a
Vậy max
0 1 2 12
; ; ; ;a a a a
=
88
8 12
2 126720aC
Ví dụ 2:
Xét khai triển
9
29
0 1 2 9
3 2 x a a x a x a x
. Tìm hệ số lớn nhất trong các hệ số
0 1 2 9
; ; ; ;a a a a
Giải
Ta có :
99
9
99
99
00
3 2 3 2 3 2
k
k k k k k k
kk
x C x C x
Vậy
9
9
3 2 ( 0,1,2, ,9)
k k k
k
a C k
Xét bất phương trình
1kk
aa
13
9 1 8 1
99
9! 9! 2 3
3 2 3 2 2 3 5 0,1,2,3,4
! 9 ! 1 ! 8 ! 9 1
k k k k k k
C C k k
k k k k k k
( do k nguyên)
Vậy
1kk
aa
5 6,7,8kk
Mặt khác
1kk
aa
5k
Vì thế ta có
0 1 2 3 4 5 6 7 8 9
a a a a a a a a a a
Từ đó:
5
5 6 0 1 9 9
max ; ; ; 2 252a a a a a C
Ví dụ 3:
Xét khai triển
2
0 1 2
2
n
n
n
x a a x a x a x
. Tìm n để
0 1 2
ax ; ; ; ;
n
M a a a a
=
10
a
Giải
Từ giả thiết
0 1 9 10 11 12
n
a a a a a a a
Ta có hệ:
10 9
10 11
aa
aa
1
2
Theo khai triển nhị thức Newton, thì
0
22
n
n
k k n k
n
k
x C x
Vậy
2
k n k
kn
aC
với k=0, 1, 2,…,n
Từ (1) ,(2)
10 10 9 9
10 10 11 11
22
22
nn
nn
nn
nn
CC
CC
14
! 2 !
12
10 !10! 9 !9!
10 9
2 ! ! 2 1
10 !10! 11 !11! 10 11
nn
nn
n
nn
n n n
29 32n
30n
hoặc
31n
.
Bài tập
1. Trong khai triển
12
12x
. Tìm hệ số lớn nhất trong các hệ số
01
, , , .
n
a a a
Đáp số:
126720.
2. Xét khai triển
13
13 12
0 1 13
3 1 .x a x a x a
Tìm hệ số lớn nhất trong các hệ
0 1 2 13
, , , , .a a a a
Đáp số:
94
4 0 1 2 13 13
max , , , , 2 366080.a a a a a C
Dạng 5: Tính bậc của khai triển Newton và bài toán liên quan
Ví dụ 1 : Với n là số nguyên dương, gọi
33n
a
là hệ số của
33n
x
trong khai triển thành đa thức
của
2
22
n
n
xx
. Tìm n để
33n
a
=26n.
Giải
Vì n nguyên dương nên
1 3 3 0nn
Theo công thức khai triển nhị thức Newton ta có:
2 0 1 2 2 4 2
1
n
nn
n n n n
x C C x C x C x
(1)
2
0 1 1 2 2 2
2 2 2 2
n n n n n
n n n n
x C C x C x C x
(2)
Nếu
1n
3n – 3 = 0
Trong trường hợp này ta có:
2
2 . 2
n
n
xx
=
2
12xx
Từ đó suy ra
0
2a
. Mặt khác 26n = 26
33
26
n
an
loại
15
Nếu
2n
, thì lập luận tương tự như trường hợp 1 cũng loại khả năng này.
Nếu
3n
, từ (1),(2) suy ra hệ số của
33n
x
trong khai triển
2
22
n
n
xx
là:
3 1 1 3 2 2
33
4 1 2
!
2 2 2 2 2
3 !3! 3
n n n n
n n n n n
n n n
n
a C C C C n n
n
Theo bài ra ta có phương trình:
2
4 1 2
2 26 5
3
n n n
n n n
( do n
3 )
Vậy
5n
là giá trị duy nhất cần tìm.
Ví dụ 2 : Tìm số tự nhiên n sao cho
1 2 2 3 3 4 2 2 1
2 1 2 1 2 1 2 1 2 1
2.2 3.2 4.2 2 1 2 2013
nn
n n n n n
C C C C n C
Giải
Xét khai triển
21
0 1 2 2 3 3 2 1 2 1
2 1 2 1 2 1 2 1 2 1
1
n
nn
n n n n n
x C xC x C x C x C
Đạo hàm hai vế
2
1 2 2 3 2 2 1
2 1 2 1 2 1 2 1
2 1 1 2 3 2 1
n
nn
n n n n
n x C xC x C n x C
Chọn
2x
, ta có:
1 2 2 3 3 4 2 2 1
2 1 2 1 2 1 2 1 2 1
2 1 2.2 3.2 4.2 2 1 2
nn
n n n n n
n C C C C n C
2 1 2013 1006nn
.
Vậy
1006n
.
Bài tập
1. Tìm số nguyên dương n sao cho
1 3 5 2 1
2 2 2 2
2048
n
n n n n
C C C C
. Đáp số
6.n
2. Tìm hệ số của
10
x
trong khai triển nhị thức
2
n
x
, biết rằng
0 1 1 2 2 3 3
3 3 3 3 1 2048
n
n n n n n n
n n n n n
C C C C C
. Đáp số
10 1
11
11; 2 22nC
.
16
3. Cho khai triển nhị thức
1 1 1 1
0 1 1
3 3 3
2 2 2 2
2 2 2 2 .2 2 . 2
n
n
x x x
x x x x
n
n n n
C C C
. Biết
31
5
nn
CC
và số hạng thứ 4 bằng
20n
. Tìm n và x. Đáp số:
7; 4.nx
Phần III: Một số dạng toán về sác xuất
Dạng 1 : Sử dụng định nghĩa xác suất cổ điển
Phương pháp:
Bước 1: Tính số phần tử của không gian mẫu
()n
.
Bước 2: Tính số phần tử của biến cố
nA
Bước 3: Xác suất của biến cố
A
là
nA
PA
n
.
Ví dụ 1 : Một chiếc hộp có 6 quả cầu trắng, 7 quả cầu xanh, 8 quả cầu đỏ. Lấy ngẫu nhiên 4 quả
cầu trong hộp. Tính xác suất để 4 quả lấy được có đủ 3 màu.
Giải
Có tất cả 21 quả cầu. Mỗi lần lấy đồng thời 4 quả cầu cho ta một tổ hợp chập 4 của 21 phần tử.
Do đó số phần tử của không gian mẫu là
4
21
5985nC
.
Gọi A là biến cố: “4 quả cầu lấy ra có đủ 3 màu’’, ta có các trường hợp (TH) sau:
TH1: Có 2 quả cầu trắng, 1 quả cầu xanh, 1 quả cầu đỏ . Số cách chọn là
2 1 1
6 7 8
840C C C
.
TH2: Có 1 quả cầu trắng, 2 quả cầu xanh, 1 quả cầu đỏ . Số cách chọn là
1 2 1
6 7 8
1008C C C
.
TH3: Có 1 quả cầu trắng, 1 quả cầu xanh, 2 quả cầu đỏ . Số cách chọn là
1 1 2
6 7 8
1176C C C
.
Ta có
3024 48
840 1008 1176 3024
5985 95
nA
n A P A
n
.
17
Ví dụ 2 : Một chiếc hộp đựng 10 tấm thẻ được đánh số
0,1,2, 8,9
. Lấy ngẫu nhiên liên tiếp 4
tấm thẻ và xếp cạnh nhau theo thứ tự từ trái sang phải. Tính xác suất để 4 thẻ xếp thành một số tự
nhiên chẵn.
Giải
Không gian mẫu gồm bộ 4 số
; ; ;a b c d
trong đó
, , ,a b c d
nhận các giá trị khác nhau trong tập
hợp
0,1,2, 8,9
nên
4
10
( ) 5040nA
.
Gọi B là biến cố: “4 thẻ xếp thành một số tự nhiên chẵn’’, gọi một số tự nhiên đó có dạng
abcd
,
ta có các trường hợp (TH) sau:
TH1:
0d
có
3
9
A
cách chọn.
TH2:
2;4;6;8d
, có 8 cách chọn
a
, hai chữ số còn lại là một chỉnh hợp chập 2 của 8 phần tử
còn lại ( khác a)
có
2
8
4.8.A
cách chọn.
Ta có
32
98
2296 41
4.8. 2296
5040 90
nA
n B A A P B
n
.
Bài tập
1. Một chiếc hộp có 5 quả cầu trắng, 6 quả cầu xanh, 7 quả cầu đỏ. Lấy ngẫu nhiên 4 quả
cầu trong hộp. Tính xác suất để 4 quả lấy được có đủ 3 màu.
Đáp số:
35
3060; 1575
68
n n A P A
.
2. Một chiếc hộp đựng 10 tấm thẻ được đánh số
0,1,2, 8,9
. Lấy ngẫu nhiên liên tiếp 4
tấm thẻ và xếp cạnh nhau theo thứ tự từ trái sang phải. Tính xác suất để 4 thẻ xếp thành
một số tự nhiên có 4 chữ số sao cho trong đó có chữ số 1.
Đáp số:
4
10
11
5040; 1848
30
n A n A P A
.
3. Có 5 học sinh nam và 3 học sinh nữ, xếp thành một hàng ngang một cách ngẫu nhiên.
Tính xác xuất để hai học sinh nũ đứng cạnh nhau.
18
HD: Gọi A là biến cố: “Không có hai hoạc sinh nữ nào đứng cạnh nhau’’, khi đó
3
6
59
8!; 5!
14 14
n n A A P A P A
.
Dạng 2 : Sử dụng quy tắc cộng và nhân xác suất
Phương pháp:
Quy tắc cộng: Nếu
A
và
B
là hai biến cố xung khắc thì
P A B P A P B
.
Quy tắc nhân: Nếu
A
và
B
là hai biến cố độc lập thì
.P A B P A P B
.
Biến cố đối: Gọi
C
là biến cố đối của biến cố
C
thì
1P C P C
.
Ví dụ 1 : Một chiếc hộp đựng 9 tấm thẻ được đánh số
1,2, 8,9
. Lấy ngẫu nhiên hai thẻ rồi
nhân hai số ghi trên hai thẻ đó với nhau. Tính xác suất để kết quả nhận được là một số chẵn.
Giải
Gọi
A
là biến cố : “Rút được một thẻ ghi số chẵn và một thẻ ghi số lẻ”.
Gọi
B
là biến cố : “Rút được cả hai thẻ ghi số lẻ”.
Kho đó biến cố: “Kết quả nhận được là một số chẵn” là
AB
.
11
54
2
9
20
36
CC
PA
C
;
2
4
2
9
6
36
C
PB
C
. Do
A
và
B
là hai biến cố xung khắc nên
20 6 13
.
36 36 18
P A B P A P B
Ví dụ 1 : Có hai túi đựng các quả cầu . Túi thứ nhất chứa 3 quả trắng, 7 quả đỏ và 15 quả xanh.
Túi thứ hai chứa 10 quả trắng, 6 quả đỏ và 9 quả xanh. Từ mỗi túi lấy ngẫu nhiên một quả cầu.
Tính xác suất để hai quả được chọn có cùng mầu.
Giải
Gọi
1
A
là biến cố : “Quả cầu lấy từ túi 1 màu trắng”
1
3
25
PA
Gọi
2
A
là biến cố : “Quả cầu lấy từ túi 2 màu trắng”
2
10
PA
19
Vì
12
,AA
là hai biến cố độc lập nên xác suất để hai quả cầu rút ra cùng màu trắng là
1 2 1 2
30
.
625
P A A P A P A
. Tương tự xác suất để hai quả cầu rút ra đều màu xanh là
15 9 135
.
25 25 625
, xác suất để hai quả cầu rút ra đều màu đỏ là
6 7 42
.
25 25 625
.
Vậy xác suất để hai quả cầu lấy ra cùng màu là :
30 135 42 207
.
625 625 625 625
Bài tập
1. Có hai túi đựng các quả cầu . Túi thứ nhất chứa 7 quả đỏ và 5 quả xanh. Túi thứ hai chứa
6 quả đỏ và 9 quả xanh. Từ mỗi túi lấy ngẫu nhiên một quả cầu.
a) Tính xác suất để hai quả được chọn có cùng mầu đỏ. Đáp số
7
20
.
b) Tính xác suất để hai quả được chọn khác mầu. Đáp số
29
60
.
2. ( TSĐH khối B, 2012) Trong một lớp học gồm có 15 học sinh nam và 10 học sinh nữ.
Giáo viên gọi ngẫu nhiên 4 học sinh lên bảng giải bài tập. Tính xác suất để 4 học sinh
được gọi có cả nam và nữ. Đáp số :
443
506
.
3. Một máy bay có ba bộ phận A, B, C có tầm quan trọng khác nhau. Máy bay sẽ rơi khi
hoặc có một viên đạn trúng vào A, hoặc hai viên đạn trúng vào B, hoặc ba viên đạn trúng
vào C. Giả sử ác bộ phận A, B, C lần lượt chiếm 15%, 30% và 55% diện ích máy bay.
Tính xác suất để máy bay này rơi nếu:
a) Máy bay bị trúng hai viên đạn. Đáp số :
0,3675
.
b) Máy bay bị trúng ba viên đạn. Đáp số :
0,72775
.
4. Có 6 học sinh nam và 4 học sinh nữ, xếp thành một hàng ngang một cách ngẫu nhiên.
Tính xác xuất để hai học sinh nũ đứng cạnh nhau. Người ta chọn một cách ngẫu nhiên 4
học sinh. Tính xác suất để 4 học sinh được chọn có ít nhất hai học sinh nữ.
HD: Gọi B là biến cố: “4 học sinh có ít nhất 2 học sinh nữ’’, khi đó
4 4 3
10 6 6
19 23
;4
242 42
n C n B C C P B P B
.
20
5. An và Bình cùng học xa nhà. Xác suất để An về nhà vào ngày Chủ nhật là
0,2
, của Bình
là
0,25
. Tính xác suất để
a) Cả hai cùng về thăm nhà. Đáp số:
0,05
;
b) Cả hai không về thăm nhà. Đáp số:
0,6
.
c) Có đúng một người về thăm nhà. Đáp số:
0,35
.
d) Có ít nhất một người về thăm nhà. Đáp số :
0,4
.
Dạng 3 : Lập bảng phân bố xác suất, tính kì vọng, phương sai của biến ngẫu nhiên rời rạc.
Phương pháp:
Kì vọng của
X
là
1 1 2 2
1
n
n n i i
i
E X x p x p x p x p
,
,( 1,2, )
ii
p P X x i n
.
Phương sai của X là
2
22
11
nn
i i i i
ii
V X x p x p
, với
EX
,( 1,2, ).
ii
p P X x i n
Ví dụ 1: Chọn ngẫu nhiên 3 đứa trẻ từ một nhóm gồm 6 bé trai và 4 bé gái. Gọi X là số bé gái
trong nhóm. Lập bảng phân bố xác suất của X.
Giải
X có thể nhận các giá trị 0, 1, 2, 3 ta có:
3
6
3
10
5
0
30
C
PX
C
;
12
46
3
10
15
1
30
CC
PX
C
;
21
46
3
10
9
2
30
CC
PX
C
;
3
4
3
10
1
3
30
C
PX
C
.
Vậy bảng phân bố xác suất của X là:
X
0
1
2
3
P
5
30
15
30
9
30
1
30
Ví dụ 2: Một hộp đựng 10 tấm thẻ, trong đó có 4 thẻ ghi số 1, ba thẻ ghi số 2, hai thẻ ghi số 3 và
một thẻ gi số 4. Chọn ngẫu nhiên hai tấm thẻ rồi cộng hai số trên hai tấm thẻ với nhau. Gọi X là
kết quả thu được.
a) Lập bảng phân bố xác suất của X ;
b) Tìm kì vọng và phương sai của X.
Giải
a) Ta có bảng phân bố xác suất của X là:
21
X
2
3
4
5
6
7
P
6
45
12
45
11
45
10
45
4
45
2
45
b)
6 12 11 10 4 2
2. 3. 4. 5. 6. 7. 4
45 45 45 45 45 45
EX
;
2 2 2 2 2 2 2
6 12 11 10 4 2
2 . 3 . 4 . 5 . 6 . 7 . 4 1,78.
45 45 45 45 45 45
VX
Bài tập
1. Một bài kiểm tra trắc nghiệm có 4 câu. Mỗi câu có 5 phương án trả lời trong đó chỉ có
một phương án trả lời đúng. Nếu trả lời đúng thì được 5 điểm. Nếu trả lời sai không được
điểm nào. Hùng làm bài thi bằng cách ở mỗi câu chọn ngẫu nhiên một phương án trả lời.
Gọi X là tổng số điểm mà Hùng đạt được.
a) Lập bảng phân bố xác suất của X.
X
0
5
10
15
20
P
0,4096
0,4096
0,1536
0,0256
0,0016
b) Tính
EX
và
VX
. Đáp số:
4; 16.E X V X
2. Một lô hàng gồm 7 sản phẩm trong đó có 3 phế phẩm. Chọn ngẫu nhiên 4 sản phẩm để
kiểm tra. Gọi X là số sản phẩm tốt thu được.
a) Lập bảng phân bố của X; Đáp số :
X
1
2
3
4
P
4
35
18
35
12
35
1
35
b) Tính
EX
. Đáp số:
16
7
EX
.