LÝ THUYẾT ĐỒ THỊ VÀ ỨNG DỤNG TRONG BÀI TOÁN TÌM ĐƢỜNG ĐI NGẮN NHẤT - Full 10 điểm

UBND TỈNH QUẢNG NAM
TRƢỜNG ĐẠI HỌC QUẢNG NAM
KHOA CÔNG NGHỆ THÔNG TIN

----------

PHONGSAVATH CHANTHAVONG

LÝ THUYẾT ĐỒ THỊ VÀ ÚNG DỤNG TRONG
BÀI TỐN TÌM ĐƢỜNG ĐI NGẮN NHẤT

KHĨA LUẬN TỐT NGHIỆP ĐẠI HỌC

Quảng Nam, tháng 05 năm 2017

UBND TỈNH QUẢNG NAM
TRƢỜNG ĐẠI HỌC QUẢNG NAM
KHOA CÔNG NGHỆ THÔNG TIN

----------

KHÓA LUẬN TỐT NGHIỆP ĐẠI HỌC

Tên đề tài: LÝ THUYẾT ĐỒ THỊ VÀ ÚNG DỤNG TRONG
BÀI TỐN TÌM ĐƢỜNG ĐI NGẮN NHẤT

Sinh viên thực hiện

PHONGSAVATH CHANTHAVONG

MSSV: 2113011004

CHUYÊN NGÀNH: CÔNG NGHỆ THÔNG TIN

KHÓA 2013 – 2017
Cán bộ hƣớng dẫn
ThS. LÊ THỊ NGUYÊN AN

MSCB: ………

Quảng Nam, tháng 05 năm 2017

LỜI CẢM ƠN

Em xin gửi lời cảm ơn chân thành và sự tri ân sâu sắc đối với các thầy cô của
trƣờng Đại học Quảng Nam, đặc biệt là các thầy cô khoa công nghệ thông tin của
trƣờng đã tạo điều kiện cho em thực tập ở khoa để có nhiều thời gian cho khóa luận tốt
nghiệp. Và em cũng xin chân thành cám ơn cô Ths. Lê Thị Nguyên An đã nhiệt tình
hƣớng dẫn hƣớng dẫn em hồn thành tốt khóa luận.

Trong q trình khóa luận, cũng nhƣ là trong q trình làm bài khóa luận tốt
nghiệp, khó tránh khỏi sai sót rất mong các thầy, cơ bỏ qua. Đồng thời do trình độ lý
luận cũng nhƣ kinh nghiệm thực tiễn còn hạn chế nên bài báo cáo khơng thể tránh khỏi
những thiếu sót, em rất mong nhận đƣợc ý kiến đóng góp của q thầy, cơ để em xin
chân thành cảm ơn.

MỤC LỤC

PHẦN 1. MỞ ĐẦU .............................................................................................. 1
1. Lý do chọn đề tài: ............................................................................................ 1
2. Mục tiêu của đề tài............................................................................................ 1
3. Đối tƣợng nghiên cứu và phạm vi nghiên cứu. ................................................ 1

4. Phƣơng pháp nghiên cứu .................................................................................. 1
5. Lịch sử nghiên cứu ........................................................................................... 2
6. Đóng góp của đề tài .......................................................................................... 2
7. Cấu trúc của đề tài ............................................................................................ 2
PHÂN 2. NỘI DUNG NGHIÊN CỨU................................................................. 2
CHƢƠNG 1 TỔNG QUAN VỀ LÝ THUYẾT ĐỒ THỊ .................................... 3
1.1 CÁC KHÁI NIỆM CƠ BẢN CỦA LÝ THUYẾT ĐỒ THỊ........................... 3
1.1.1 Định nghĩa đồ thị ......................................................................................... 3
1.1.2. Định nghĩa đƣờng đi, chu trình, đồ thị liên thơng. ..................................... 5
1.2 CÁC KHÁI NIỆM VỀ ĐƢỜNG ĐI NGẮN NHẤT...................................... 8
1.2.1 Mở đầu......................................................................................................... 8
1.2.2 Đƣờng đi ngắn nhất xuất phát từ một đỉnh.................................................. 9
1.2.3 Đƣờng đi trong đồ thị khơng có chu trình. ................................................ 10
CHƢƠNG 2 MỘT SỐ THUẬT TỐN TÌM ĐƢỜNG ĐI NGẮN NHẤT
TRÊN ĐỒ THỊ ................................................................................................... 12
2.1. MỘT SỐ KHÁI NIỆM ................................................................................ 12
2.2. ĐƢỜNG ĐI NGẮN NHẤT XUẤT PHÁT TỪ MỘT ĐỈNH...................... 13
2.2.1 Đƣờng đi ngắn nhất xuất phát từ một đỉnh. Thuật tốn Ford-Bellman ..... 13
2.2.2. Tìm đƣờng đi ngắn nhất bằng thuật toán Dijkstra .................................... 15
2.3. ĐƢỜNG ĐI NGẮN NHẤT GIỮA CÁC CẶP ĐỈNH ................................ 17
2.3.1. Phát biểu bài tốn tìm đƣờng đi ngắn nhất ............................................... 17
2.3.2. Thuật toán Floyd....................................................................................... 18
CHƢƠNG 3 XÂY DỰNG ỨNG DỤNG ........................................................... 22
3.1. GIỚI THIỆU................................................................................................ 22
3.2. XÂY DỰNG ỨNG DỤNG ......................................................................... 22

3.2.1. Xây dựng lớp thƣ viện Node: ................................................................... 22
3.2.2. Xây dựng lớp thƣ viện Matrix: ................................................................. 25
3.2.3. Xây dựng lớp Edge:.................................................................................. 34
3.3. Xây dựng form giao diện của chƣơng trình................................................. 39

3.4. Kết quả chạy chƣơng trình ......................................................................... 57
PHẦN 3. KẾT LUẬN ........................................................................................ 58
PHẦN 4. TÀI LIỆU THAM KHẢO .................................................................. 59

DANH MỤC HÌNH ẢNH

Hình 1. Sơ đồ mạng máy tính .................................................................................................. 3
Hình 2. Sơ đồ mạng máy tính với đa kênh thoại ................................................................... 4
Hình 4. Mạng máy tính với các kênh thoại một chiều .......................................................... 5
Hình 5. Đƣờng đi trên đồ thị ................................................................................................... 6
Hình 7. Đồ thị liên thông mạnh g, đồ thị liên thông yếu h .................................................... 8
Hình 8. Đồ thị khơng có chu trình ............................................................................ 10
Hình 9. Minh họa thuật tốn ford_bellman. ........................................................................ 14
Hình 10. Đồ thị ví dụ ............................................................................................................. 16
Hình 11. Mảng lƣu trữ tạm thời............................................................................................18
Hình 12. Chƣơng trình demo .................................................................................... 39
Hình 13. Kết quả chƣơng trình................................................................................ 57

PHẤN 1. MỞ ĐẦU

1. Lý do chọn đề tài:
Lý thuyết đồ thị đƣợc đề xuất từ những năm đầu của thế kỷ 18 bởi nhà toán học

ngƣời Thụy Sĩ Leonhard Euler. Ông là ngƣời đã sử dụng đồ thị để giải bài toán nổi
tiếng về các cây cầu ở thành phố Konigsberg. Từ đó lý thuyết đồ thị đƣợc áp dụng
rộng rãi và ngày càng khẳng định đƣợc vị trí quan trọng khi đƣợc áp dụng để giải
quyết các bài toán thực tế.

Lý thuyết đồ thị cũng là công cụ đắc lực cho ngành công nghệ thơng tin. Nó giúp
cho chúng ta mơ tả một các dễ dàng các bài toán phức tạp thành cụ thể, để từ đó ta có

thể mã hóa các bài tốn đó vào máy tính.

Hiện nay có rất nhiều thuật tốn để tìm đƣờng đi ngắn nhất trong đồ thị nhƣ:
thuật toán Ford-Bellman, thuật tốn Dijkstra, thuật tốn Floyd...để tìm hiểu rõ hơn về
các thuật toán này cũng nhƣ ứng dụng hiệu quả các thuật tốn này trong thực tế, đó là
lý do em chọn đề tài “ Lý thuyết đồ thị và ứng dụng trong bài tốn tìm đƣờng đi ngắn
nhất để làm đề tài khóa luận tốt nghiệp ”. Nội dung của khóa luận bao gồm những
phần sau:

 Chƣơng 1 : Tổng quan về lý thuyết đồ thị.
 Chƣơng 2 : Một số thuật tốn tìm đƣờng đi ngắn nhất trên đồ thị.
 Chƣơng 3 : Đánh giá và cài đặt.
2. Mục tiêu của đề tài.
- Hiểu rõ đƣợc những khái niệm cơ bản của lý thuyết đồ thị.
- Nắm vững một số thuật tốn tìm đƣờng đi ngắn nhất của đồ thị
- Xây dựng ứng dụng thuật tốn Floyd để tìm đƣờng đi ngắn nhất trong thực tế
3. Đối tƣợng nghiên cứu và phạm vi nghiên cứu.
- Lý thuyết về lý thuyết đồ thị
- Một số thuật tốn tìm đƣờng đi ngắn nhất trên đồ thị
- Nghiên cứu thuật toán Floyd và xây dựng ứng dụng thực tế
4. Phƣơng pháp nghiên cứu
- Tìm hiểu thu thập tài liệu liên quan đến lý thuyết đồ thị và một số thuật tốn tìm
đƣờng đi ngắn nhất trên đồ thị
- Kết hợp tìm hiểu so sánh tổng hợp đánh giá các thuật tốn tìm đƣờng đi ngắn
nhất trên đồ thị
- Demo tìm đƣờng đi ngắn nhất tối ƣu

Trang 1

5. Lịch sử nghiên cứu

- Nội dung đã đƣợc dạy và học ở phần Tốn rời rạc

- Có nhiều cá nhân cũng nhƣ nhóm nghiên cứu đã chọn kiến thức này làm nội

dụng cho đề tài nghiên cứu của họ.

6. Đóng góp của đề tài

- Cung cấp kiến thức đầy đủ hơn, chi tiết hơn về lý thuyết đồ thị cũng nhƣ các

phƣơng pháp tìm đƣờng đi ngắn nhất trên đồ thị

- Demo thuật tốn tìm đƣờng đi ngắn nhất tối ƣu trong thực tế

7. Cấu trúc của đề tài

Chƣơng 1 : Tổng quan về lý tuyết đồ thị

 Nghiên cứu, tìm hiểu tổng quan, trích chọn và trình bày một số khái

niệm cơ bản về lý thuyết đồ thị

Chƣơng 2 : Một số thuật tốn tìm đƣờng đi ngắn nhất trên đồ thị

 Trình bày một số phƣơng pháp tìm đƣờng đi ngắn nhất trên đồ thị

Chuong 3 : Đánh giá phƣơng pháp và cài đặt.

 So sánh đánh giá các phƣơng pháp. Demo thuật toán tối ƣu trong tìm đƣờng

đi ngắn nhất.

Trang 2

PHẦN 2. NỘI DUNG
CHƢƠNG 1

TỔNG QUAN VỀ LÝ THUYẾT ĐỒ THỊ
1.1 CÁC KHÁI NIỆM CƠ BẢN CỦA LÝ THUYẾT ĐỒ THỊ

1.1.1 Định nghĩa đồ thị
Đồ thị là một cấu trúc rời rạc bao gồm các đỉnh và các cạnh nối các đỉnh này.

Chúng ta phân biệt các loại đồ thị khác nhau bởi kiểu và số lƣợng cạnh nối hai đỉnh
nào đó của đồ thị. Để có thể hình dung đƣợc tại sao lại cần đến các loại đồ thị khác
nhau, chúng ta sẽ nêu ví dụ sử dụng chúng để mơ tả một mạng máy tính. Giả sử ta có
một mạng gồm các máy tính và các kênh điện thoại nối các máy tính này. Chúng ta có
thể biểu diễn các vị trí đặt máy tính bởi các điểm và các kênh thoại nối chúng bởi các
đoạn nối.

Hình 1. Sơ đồ mạng máy tính
Nhận thấy rằng trong sơ đồ mạng máy tính ở hình 1, giữa hai máy tính bất kỳ chỉ
cho phép nhiều nhất là một kênh thoại nối chúng, kênh thoại này cho phép liên lạc cả
hai chiều và khơng có máy tính nào lại đƣợc nối với chính nó. Sơ đồ mạng máy tính
cho trong hình 1 đƣợc gọi là đơn đồ thị vơ hướng từ đó ta đi đến một định nghĩa sau:
Định nghĩa 1. Đơn đồ thị vô hướng G=(V,E) bao gồm V là tập đỉnh, và E là tập
các cặp khơng có thứ tự gồm hai phần tử khác nhau của V gọi là các cạnh.
Trong trƣờng hợp giữa hai máy tính nào đó thƣờng xun phải truyền tải nhiều
thơng tin buộc lòng ngƣời ta phải nối hai máy này bởi nhiều kênh thoại. Lúc này ta có

mơ hình mạng máy tính mới đƣợc sinh ra nhƣ sau:

Trang 3

Hình 2. Sơ đồ mạng máy tính với đa kênh thoại
Từ đó chúng ta có thêm một định nghĩa tiếp theo nhƣ sau:
Định nghĩa 2. Đa đồ thị vô hướng G=(V,E) bao gồm V là tập các đỉnh, và E là
họ các cặp khơng có thứ tự gồm hai phần tử khác nhau của V gọi là các cạnh. Hai
cạnh e1 va e2 được gọi là cạnh lặp nếu chúng cùng tương ứng với một cặp đỉnh.

Hình 3. Sơ đồ mạng máy tính với kênh thơng báo.
Rõ ràng mỗi đơn đồ thị đều là đa đồ thị, nhƣng không phải đa đồ thị nào cũng là
đơn đồ thị, vì trong đa đồ thị có hai hay nhiều hơn cạnh nối một cặp đỉnh nào đó.
Trong mạng máy tính có thể có những kênh thoại nối một máy tính nào đó với
chính nó (chẳng hạn với mục đích thơng báo). Mạng nhƣ vậy đƣợc cho trong hình 3.
Nhƣ vậy đa đồ thị không thể mô tả đƣợc mạng nhƣ vậy, bởi vì có những khun (cạnh
nối một đỉnh vói chính nó). Trong trƣờng hợp này chúng ta cần sử dụng đến khái niệm
giả đồ thị vô hƣớng, đƣợc định nghĩa nhƣ sau:
Định nghĩa 3. Giả đồ thị vô hướng G=(V,E) bao gồm V là tập các đỉnh, và E là
họ các cặp không có thứ tự gồm hai phần tử (khơng nhất thiết phải khác nhau) của V
gọi là các cạnh. Cạnh e được gọi là khuyên nếu có dạng e=(u,u).

Trang 4

Các kênh thoại trong mạng máy tính có thể chỉ cho phép truyền tin theo một
chiều. Chẳng hạn trong hình 4 máy chủ ở Hà Nội chỉ có thể nhận tin từ các máy ở địa
phƣơng, có một số máy chỉ có thể gửi tin đi, còn các kênh thoại cho phép truyền tin
theo cả hai chiều đƣợc thay thế bởi hai cạnh có hƣớng ngƣợc chiều nhau.

Hình 4. Mạng máy tính với các kênh thoại một chiều

Ta đi đến định nghĩa sau:
Định nghĩa 4. Đơn đồ thị có hướng G=(V,E) bao gồm V là tập các đỉnh và E là
tập các cặp có thứ tự gồm hai phần tử khác nhau của V gọi là các cung.
Nếu trong mạng có thể có đa kênh thoại một chiều, ta sẽ phải sử dụng đến khái
niệm đa đồ thị có hướng:
Định nghĩa 5. Đa đồ thị có hướng G=(V,E) bao gồm V là tập các đỉnh, và E là
họ các cặp có thứ tự gồm hai phần tử khác nhau của V gọi là các cung. Hai cung e1 va
e2 tương ứng với cùng một cặp đỉnh được gọi là cung lặp.
1.1.2. Định nghĩa đƣờng đi, chu trình, đồ thị liên thơng
Định nghĩa 1. Đường đi độ dài n từ đỉnh u đến đỉnh v, trong đó n là số nguyên
dương, trên đồ thị vô hướng G=(V,E) là dãy xo, x1 , ... , xn-1 , xn
trong đó u=x0 , v=xn , ( xi , xi+1 ) E , i= 0, 1, 2 ,..., n-1.
Đường đi nói trên cịn có thể biểu diễn dưới dạng các cạnh:
(x0 , x1 ) , ( x1 , x2), ... , ( xn-1 , xn ).
Đỉnh u gọi là đỉnh đầu, còn đỉnh v gọi là đỉnh cuối của đường đi. Đường đi có
đỉnh đầu trùng với đỉnh cuối (tức là u=v) được gọi là chu trình. Đường đi hay chu
trình được gọi là đơn nếu như khơng có cạnh nào bị lặp lại.
Ví dụ 1. Trên đồ thị vơ hƣớng cho trong hình 1: a,d,c,f,e là đƣờng đi đơn độ dài
4. Cịn d,e,c,a khơng là đƣờng đi do (e,c) không phải là cạnh của đồ thị. Dãy b,c,f,e,b

Trang 5

là chu trình độ dài 4. Đƣờng đi a,b,e,d,a,b có độ dài là 5 không phải là đƣờng đi đơn,
do cạnh (a,b) có mặt trong nó hai lần.

Hình 5. Đường đi trên đồ thị
Khái niệm đƣờng đi và chu trình trên đồ thị có hƣớng đƣợc định nghĩa hoàn
toàn tƣơng tự nhƣ trƣờng hợp đồ thị vô hƣớng, chỉ khác là ta chú ý đến hƣớng trên các
cung.
Định nghĩa 2. Đường đi độ dài n từ đỉnh u đến đỉnh v, trong đó n là số nguyên

dương, trên đồ thị có hướng G=(V,A) là dãy xo, x1 , ... , xn-1 , xn
trong đó u=x0 , v=xn , ( xi , xi+1 )  A , i= 0, 1, 2 ,..., n-1.
Đường đi nói trên cịn có thể biểu diễn dưới dạng các cung:
(x0 , x1 ) , ( x1 , x2), ... , ( xn-1 , xn ).
Đỉnh u gọi là đỉnh đầu, còn đỉnh v gọi là đỉnh cuối của đường đi. Đường đi có
đỉnh đầu trùng với đỉnh cuối (tức là u=v) được gọi là chu trình. Đường đi hay chu
trình được gọi là đơn nếu như khơng có cung nào bị lặp lại.
Ví dụ 2. Trên đồ thị có hƣớng cho trong hình 1: a,d,c,f,e là đƣờng đi đơn độ dài
4. Cịn d,e,c,a khơng là đƣờng đi do (e,c) không phải là cung của đồ thị. Dãy b,c,f,e,b
là chu trình độ dài 4. Đƣờng đi a,b,e,d,a,b có độ dài là 5 khơng phải là đƣờng đi đơn,
do cung (a,b) có mặt trong nó hai lần.
Xét một mạng máy tính. Một câu hỏi đặt ra là hai máy tính bất kỳ trong mạng
này có thể trao đổi đƣợc thông tin với nhau hoặc trực tiếp qua kênh nối chúng hợăc
thơng qua một hoặc vài máy tính trung gian trong mạng? Nếu sử dụng đồ thị để biểu
diễn mạng máy tính này (trong đó các đỉnh của đồ thị tƣơng ứng với các máy tính, cịn
các cạnh tƣơng ứng với các kênh nối) câu hỏi đó đƣợc phát biểu trong ngôn ngữ đồ thị
nhƣ sau: Tồn tại hay chăng đƣờng đi giữa mọi cặp đỉnh của đồ thị ?
Định nghĩa 3. Đồ thị vô hướng G=(V,E) được gọi là liên thông nếu ln tìm
được đường đi giữa hai đỉnh bất kỳ của nó.
Nhƣ vậy hai máy tính bất kỳ trong mạng có thể trao đổi thơng tin đƣợcvới nhau
khi và chỉ khi đồ thị tƣơng ứng với mạng này là đồ thị liên thông.

Trang 6

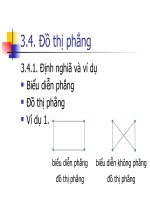
Ví dụ 3. Trong hình 6: Đồ thị G là liên thơng, đồ thị H là không liên thông

Hình 6. Đồ thị liên thơng G và đồ thị H gồm 3 thành phần liên thông H1,H2,H3.
Định nghĩa 4. Ta gọi đồ thị con của đồ thị G=(V,E) là đồ thị H=(W,F), trong đó
W  V và F  E
Trong trƣờng hợp đồ thị là khơng liên thơng, nó sẽ rã ra thành một số đồ thị con

liên thơng đơi một khơng có đỉnh chung. Những đồ thị con liên thông nhƣ vậy ta sẽ gọi
là các thành phần liên thông của đồ thị.
Trong mạng máy tính có thể có những máy (những kênh nối) mà sự hỏng hóc
của nó có thể ảnh hƣởng đến việc trao đổi thơng tin trong mạng. Các khái niệm tƣơng
ứng với tình huống này đƣợc đƣa ra trong định nghĩa sau.
Định nghĩa 5. Đỉnh v được gọi là đỉnh rẽ nhánh nếu việc loại bỏ v cùng với các
cạnh liên thuộc với nó khỏi đồ thị làm tăng số thành phần liên thông của đồ thị. Cạnh
e được gọi là cầu nếu việc loại bỏ nó khỏi đồ thị làm tăng số thành phần liên thông
của đồ thị..
Ví dụ 5. trong đồ thị G ở hình 2, đỉnh d và e là đỉnh rẽ nhánh, còn các cạnh (d,g)
và (e,f) là cầu.Đối với đồ thị có hƣớng có hai khái niệm liên thơng phụ thuộc vào việc
ta có xét đến hƣớng trên các cung hay không.
Định nghĩa 6. Đồ thị có hướng G=(V,A) được gọi là liên thơng mạnh nếu ln
tìm được đường đi giữa hai đỉnh bất kỳ của nó.
Định nghĩa 7. Đồ thị có hướng G=(V,A) được gọi là liên thông yếu nếu đồ thị
vô hướng tương ứng với nó là đồ thị vơ hướng liên thơng.
Rõ ràng nếu đồ thị là liên thơng mạnh thì nó cũng là liên thơng yếu, nhƣng điều
ngƣợc lại là không luôn đúng, nhƣ chỉ ra trong ví dụ dƣới đây.

Trang 7

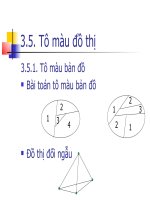
Ví dụ 6. Trong hình 3 đồ thị G là liên thơng mạnh, cịn H là liên thông yếu
nhƣng không là liên thông mạnh

Hình 7. Đồ thị liên thông mạnh G, đồ thị liên thông yếu H
1.2 CÁC KHÁI NIỆM VỀ ĐƢỜNG ĐI NGẮN NHẤT.
1.2.1 Mở đầu

Trong phần này chúng ta chỉ xét đồ thị có hƣớng G=(V,E) và |V|=n,|E|=m với
các cung đƣợc gán trọng số, nghĩa là, mỗi cung (u,v)E của nó đƣợc đặt tƣơng ứng

với một số thực a(u,v) gọi là trọng số của nó. Chúng ta sẽ đặt a(u,v)=  , nếu (u,v)E .
Nếu dãy v0, v1 , ... , vp là một đƣờng đi trên G, thì độ dài của nó đƣợc định nghĩa là
tổng sau:

tức là, độ dài của đƣờng đi chính là tổng các trọng số trên các cung của nó. (Chú
ý rằng nếu chúng ta gán trọng số cho tất cả các cung đều bằng 1, thì ta thu đƣợc định
nghĩa độ dài đuờng đi nhƣ là số cung của đƣờng đi.

Bài tốn tìm đƣờng đi ngắn nhất trên đồ thị dƣới dạng tổng quát có thể đƣợc
phát biểu dƣới dạng tổng quát nhƣ sau: Tìm đƣờng đi có độ dài nhỏ nhất từ một đỉnh
xuất phát sV đến đỉnh cuối (đích) tV. Đƣờng đi nhƣ vậy sẽ gọi là đường đi ngắn
nhất từ s đến t cịn độ dài của nó sẽ kí hiệu là d(s,t) và còn gọi là khoảng cách từ s
đến t (khoảng cách định nghĩa nhƣ vậy có thể là số âm). Nếu nhƣ không tồn tại đƣờng
đi từ s đến t thì ta đặt d(s,t)=  từ đó ta thấy chu trình trong đồ thị có độ dài dƣơng, thì
trong đƣờng đi ngắn nhất khơng có đỉnh nào lặp lại (đƣờng đi nhƣ thế gọi là đường đi
cơ bản).

Trang 8

Mặt khác, nếu trong đồ thị có chu trình với độ dài âm (gọi là chu trình âm) thì
khoảng cách giữa 1 số cặp đỉnh nào đó của đồ thị có thể là khơng xác định, bởi vì,
bằng cách đi vịng theo chu trình này một số đủ lớn lần, ta có thể chỉ ra đƣờng đi giữa
các đỉnh này có độ dài nhỏ hơn bất kì số thực cho trƣớc nào. Trong truờng hợp nhƣ
vậy, có thể đặt vấn đề tìm đƣờng đi cơ bản ngắn nhất, tuy nhiên bài toán đặt ra sẽ trở
nên phức tạp hơn rất nhiều, bởi vì nó chứa bài toán xét sự tồn tại đƣờng đi Hamilton
trong đồ thị nhƣ là một trƣờng hợp riêng.

Trƣớc hết cần chú ý rằng nếu biết khoảng cách từ s đến t, thì đƣờng đi ngắn
nhất từ s đến t, trong trƣờng hợp trọng số khơng âm, có thể tìm một cách dễ dàng. Để
tìm đƣờng đi, chỉ cần chú ý là đối với cặp đỉnh s,tV tuỳ ý (s  t) luôn tìm đƣợc đỉnh v

sao cho: d(s,t) = d(s,v) + a(v,t)

Thật vậy đỉnh v nhƣ vậy chính là đỉnh đi trƣớc đỉnh t trong đƣờng đi ngắn nhất từ
s đến t. Tiếp theo ta có thể tìm đƣợc u sao cho d(s,v)=d(s,u)+a(u,v),... Từ giả thiết về
tính khơng âm của các trọng số dễ dàng suy ra rằng dãy t,v,u... không chứa đỉnh lặp lại
và kết thúc ở đỉnh s. Rõ ràng dãy thu đƣợc xác định đƣờng đi ngắn nhất từ s đến t.
1.2.2 Đƣờng đi ngắn nhất xuất phát từ một đỉnh

Phần lớn các thuật toán tìm khoảng cách giữa hai đỉnh s và t đƣợc xây dựng nhờ
kỹ thuật tính tốn mà ta có thể mô tả nhƣ sau: từ ma trận trọng số a[u,v],u,vV, ta tính
cận trên d[v] của khoảng cách từ s đến tất cả các đỉnh vV. Mỗi khi phát hiện
d[u]+a[u,v]
Q trình đó sẽ kết thúc khi nào chúng ta không làm tốt thêm đƣợc bất cứ cận
trên nào. Khi đó, rõ ràng giá trị của mỗi d[v] sẽ cho ta khoảng cách từ mỗi đỉnh s đến
v. Khi thể hiện kỹ thuật tính tốn này trên máy tính, cận trên d[v] sẽ đƣợc gọi là nhãn
của đỉnh v, cịn việc tính lại các cận trên này sẽ gọi là phép gán nhãn cho đồ thị và toàn
bộ thủ tục thƣờng gọi là thủ tục gán nhãn. Nhận thấy rằng để tính khoảng cách từ s đến
tất cả các đỉnh còn lại của đồ thị. Hiện nay vẫn chƣa biết thuật tốn nào cho phép tìm
đƣờng đi ngắn nhất giữa hai đỉnh làm việc thực sự hiệu quả hơn những thuật tốn tìm
đƣờng đi ngắn nhất từ một đỉnh đến tất cả các đỉnh còn lại.

Sơ đồ tính tốn mà ta vừa mơ tả cịn chƣa là xác định, bởi vì cịn phải chỉ ra thứ
tự chọn các đỉnh u và v để kiểm tra điều kiện. Thứ tự chọn này có ảnh hƣởng rất lớn
đến hiệu quả thuật toán.

Trang 9

1.2.3 Đƣờng đi trong đồ thị khơng có chu trình.
Bây giờ ta xét trƣờng hợp riêng thứ hai của bài tốn tìm đƣờng đi ngắn nhất, mà

để giải nó có thể xây dựng thuật tốn với độ phức tạp tính tốn O(n2), đó là đồ thị
khơng có chu trình (cịn trọng số trên các cung có thể là các số thực tuỳ ý). Trƣớc hết
ta chứng minh định lý sau.

Định lý 2. Giả sử G là đồ thị khơng có chu trình. Khi đó các đỉnh của nó có thể
đánh số sao cho mỗi cung của đồ thị chỉ hướng từ đỉnh có chỉ số nhỏ hơn đến đỉnh có
chỉ số lớn hơn, nghĩa là mỗi cung của nó có thể biểu diễn dưới dạng (v[i],v[j]), trong
đó i
Ví dụ 3. Đồ thị trong hình sau có các đỉnh đƣợc đánh số thỏa mãn điều kiện nêu
trong định lý.

Hình 8. Đồ thị khơng có chu trình
Để chứng minh định lý ta mơ tả thuật tốn sau, cho phép tìm ra cách đánh số thỏa
mãn điều kiện định lý.
Void Numbering;
Đầu vào: Đồ thị có hướng G=(V,E) với n đỉnh khơng chứa chu trình được cho
bởi danh sách kề Ke(v),v V

Đầu ra: Với mỗi đỉnh v V chỉ số NR[u] < NR[v].
{

For v V do Vao[v]:=0;
(* tinh Vao[v]=deg-(v) *)
For u V do
For vKe(u) do Vao[v]:=Vao[v] + 1;
QUEUE:=  ;
For v V do
If Vao[v]=0 then QUEUE  v ;

Num :=0;

Trang 10

While QUEUE   do
{
u  QUEUE;
Num :=num +1; NR[u] :=num;
For vKe(u) do
{

Vao[v]:=Vao[v] - 1;
If Vao[v]=0 then QUEUE  v ;

}
}
}
Thuật toán đƣợc xây dựng dựa trên ý tƣởng rất đơn giản sau: Rõ ràng trong đồ
thị khơng có chu trình bao giờ cũng tìm đƣợc đỉnh có bán bậc vào bằng 0 (khơng có
cung đi vào). Thực vậy, bắt đầu từ đỉnh v1 nếu có cung đi vào nó từ v2 thì ta lại
chuyển sang xét đỉnh v2. Nếu có cung v3 đi vào v2, thì ta chuyển sang xét v3... Do đồ
thị là khơng có chu trình nên sau một số hữu hạn lần chuyển nhƣ vậy ta phải đi đến
đỉnh khơng có cung đi vào. Thoạt tiên, tìm các đỉnh nhƣ vậy của đồ thị . Rõ ràng ta
có thể đánh số chúng theo một thứ tự tuỳ ý bắt đầu từ 1. Tiếp theo, loại bỏ khỏi đồ thị
những đỉnh đã đƣợc đánh số cùng các cung đi ra khỏi chúng, ta thu đƣợc đồ thị mới
cũng khơng có chu trình, và thủ tục đƣợc lặp lại với đồ thị mới này. Q trình đó sẽ
đƣợc tiếp tục cho đến khi tất cả các đỉnh của đồ thị đƣợc đánh số.

Trang 11

CHƢƠNG 2
MỘT SỐ THUẬT TOÁN
TÌM ĐƢỜNG ĐI NGẮN NHẤT TRÊN ĐỒ THỊ

2.1. MỘT SỐ KHÁI NIỆM
Xét đồ thị có hƣớng G=(V,E), |V|=n, |E|=m với các cung đƣợc gán trọng số,

nghĩa là, mỗi cung (u, v) E của nó đƣợc đặt tƣơng ứng với một số thực a(u, v) gọi là
trọng số của nó. Chúng ta sẽ đặt a(u, v) = , nếu (u,v) E. Nếu dãy v0, v1,..., vp là
một đƣờng đi trên G, thì độ dài của nó đƣợc định nghĩa là tổng sau

∑

tức là, độ dài của đƣờng đi chính là tổng của các trọng số trên các cung của nó.
(Chú ý rằng nếu chúng ta gán trọng số cho tất cả cung đều bằng 1, thì ta thu đƣợc định
nghĩa độ dài của đƣờng đi nhƣ là số cung của đƣờng đi giống nhƣ trong các chƣơng
trƣớc đã xét).

Bài tốn tìm đƣờng đi ngắn nhất trên đồ thị dƣới dạng tổng qt có thể phát biểu
nhƣ sau: tìm đƣờng đi có độ dài nhỏ nhất từ một đỉnh xuất phát s V đến đỉnh cuối
(đích) t V. Đƣờng đi nhƣ vậy ta sẽ gọi là đƣờng đi ngắn nhất từ s đến t cịn độ dài
của nó ta sẽ ký hiệu là d(s, t) và còn gọi là khoảng cách từ s đến t (khoảng cách định
nghĩa nhƣ vậy có thể là số âm). Nếu nhƣ không tồn tại đƣờng đi từ s đến t thì ta sẽ đặt
d(s, t)= . Rõ ràng, nếu nhƣ mỗi chu trình trong đồ thị đều có độ dài dƣơng, trong
đƣờng đi ngắn nhất khơng có đỉnh nào bị lặp lại (đƣờng đi khơng có đỉnh lặp lại sẽ gọi
là đƣờng đi cơ bản). Mặt khác nếu trong đồ thị có chu trình với độ dài âm (chu trình
nhƣ vậy để gọi ngắn gọn ta gọi là chu trình âm) thì khoảng cách giữa một số cặp đỉnh
nào đó của đồ thị có thể là khơng xác định, bởi vì, bằng cách đi vịng theo chu trình
này một số đủ lớn lần, ta có thể chỉ ra đƣờng đi giữa các đỉnh này có độ dài nhỏ hơn
bất cứ số thực cho trƣớc nào. Trong những trƣờng hợp nhƣ vậy, có thể đặt vấn đề tìm

đƣờng đi cơ bản ngắn nhất, tuy nhiên bài tốn đặt ra sẽ trở nên phức tạp hơn rất nhiều,
bởi vì nó chứa bài tốn xét sự tồn tại đƣờng đi Hamilton trong đồ thị nhƣ là một
trƣờng hợp riêng.

Trƣớc hết cần chú ý rằng nếu biết khoảng cách từ s đến t, thì đƣờng đi ngắn nhất
từ s đến t, trong trƣờng hợp trọng số khơng âm, có thể tìm đƣợc một cách dễ dàng. Để

Trang 12

tìm đƣờng đi, chỉ cần để ý là đối với cặp đỉnh s, t V tuỳ ý (s <> t) ln tìm đƣợc đỉnh
v sao cho d(s, t) = d(s, v) + a(v, t).

Thực vậy, đỉnh v nhƣ vậy chính là đỉnh đi trƣớc đỉnh t trong đƣờng đi ngắn nhất
từ s đến t. Tiếp theo ta lại có thể tìm đƣợc đỉnh u sao cho d(s, v) = d(s, u) + a(u,v), ...
Từ giả thiết về tính khơng âm của các trọng số dễ dàng suy ra rằng dãy t, v, u, ...
không chứa đỉnh lặp lại và kết thúc ở đỉnh s. Rõ ràng dãy thu đƣợc xác định (nếu lật
ngƣợc thứ tự các đỉnh trong nó) đƣờng đi ngắn nhất từ s đến t. Từ đó ta có thuật tốn
sau đây để tìm đƣờng đi ngắn nhất từ s đến t khi biết độ dài của nó.

Chú ý rằng độ phức tạp tính tốn của thuật tốn là O(n2), do để tìm đỉnh u ta phải
xét qua tất cả các đỉnh của đồ thị. Tất nhiên, ta cũng có thể sử dụng kỹ thuật ghi nhận
đƣờng đi đã trình bày trong chƣơng 3: dùng biến mảng Truoc[v], v V, để ghi nhớ
đỉnh đi trƣớc v trong đƣờng đi tìm kiếm.

Cũng cần lƣu ý thêm là trong trƣờng hợp trọng số trên các cạnh là khơng âm,
bài tốn tìm đƣờng đi ngắn nhất trên đồ thị vơ hƣớng có thể dẫn về bài tốn trên đồ thị
có hƣớng, bằng cách thay đổi mỗi cạnh của nó bởi nó bởi hai cung có hƣớng ngƣợc
chiều nhau với cùng trọng số là trọng số của các cạnh tƣơng ứng. Tuy nhiên, trong
trƣờng hợp có trọng số âm, việc thay nhƣ vậy có thể dẫn đến chu trình âm.
2.2. ĐƢỜNG ĐI NGẮN NHẤT XUẤT PHÁT TỪ MỘT ĐỈNH

2.2.1 Đƣờng đi ngắn nhất xuất phát từ một đỉnh. Thuật toán Ford-Bellman

Phần lớn các thuật tốn tìm khoảng cách giữa hai đỉnh s và t đƣợc xây dựng nhờ
kỹ thuật tính tốn mà ta có thể mơ tả đại thể nhƣ sau: từ ma trận trọng số a[u, v], u, v
V, ta tính cận trên d[v] của khoảng cách từ s đến tất cả các đỉnh v V. Mỗi khi phát
hiện d[u] + a[u,v] < d[v] (1) cận trên d[v] sẽ đƣợc làm tốt lên: d[v] + a[u, v].

Quá trình đó sẽ kết thúc khi nào chúng ta khơng làm tốt thêm đƣợc bất kỳ cận
trên nào. Khi đó, rõ ràng giá trị của mỗi d[v] sẽ cho khoảng cách từ đỉnh s đến đỉnh v.
Khi thể hiện kỹ thuật tính tốn này trên máy tính, cận trên d[v] sẽ đƣợc gọi là nhãn của
đỉnh v, cịn việc tính lại các cận này sẽ đƣợc gọi là thủ tục gán. Nhận thấy rằng để tính
khoảng cách từ s đến t, ở đây, ta phải tính khoảng cách từ s đến tất cả các đỉnh còn lại
của đồ thị. Hiện nay vẫn chƣa biết thuật tốn nào cho phép tìm đƣờng đi ngắn nhất
giữa hai đỉnh làm việc thực sự hiệu quả hơn những thuật tốn tìm đƣờng đi ngắn nhất
từ một đỉnh đến tất cả các đỉnh còn lại.

Trang 13

Sơ đồ tính tốn mà ta vừa mơ tả cịn chƣa xác định, bởi vì cịn phải chỉ ra thứ tự
các đỉnh u và v để kiểm tra điều kiện (1). Thứ tự chọn này có ảnh hƣởng rất lớn đến
hiệu quả của thuật toán.

Bây giờ ta sẽ mơ tả tht tốn Ford-Bellman tìm đƣờng đi ngắn nhất từ đỉnh s
đến tất cả các đỉnh còn lại của đồ thị. Thuật toán làm việc trong trƣờng hợp trọng số
của các cung là tuỳ ý, nhƣng giả thiết rằng trong đồ thị khơng có chu trình âm.

Tính đúng đắn của thuật tốn có thể chứng minh trên cơ sở trên nguyên lý tối ƣu
của quy hoạch động. Rõ ràng là độ phức tạp tính tốn của thuật tốn là O(n3). Lƣu ý
rằng chúng ta có thể chấm dứt vịng lặp theo k khi phát hiện trong q trình thực hiện
hai vịng lặp trong khơng có biến d[v] nào bị đổi giá trị. Việc này có thể xảy ra đối với

k < n-2, và điều đó làm tăng hiệu quả của thuật tốn trong việc giải các bài toán thực
tế. Tuy nhiên, cải tiến đó khơng thực sự cải thiện đƣợc đánh giá độ phức tạp của bản
thân thuật toán. Đối với đồ thị thƣa tốt hơn là sử dụng danh sách kề Ke(v), v V

Trong trƣờng hợp này ta thu đƣợc thuật toán với độ phức tạp O(n, m).
xét đồ thị trong hình 7.1. Các kết quả tính tốn theo thuật tốn đƣợc mơ tả trong

bảng dƣới đây

Hình 9. Minh họa thuật toán Ford_Bellman.

k d[1] Truoc[1] d[2] Truoc[2] d[3] Truoc[3] d[4] Truoc[4] d[5] Truoc[5]

0, 1 1, 1 ∞, 1 ∞, 1 3, 1

1 0, 1 1, 1 4, 2 4, 2 -1, 3

2 0, 1 1, 1 4, 2 3, 5 -1, 3

3 0, 1 1, 1 4, 2 3, 5 -1, 3

Bảng kết quả tính tốn theo thuật tốn Ford_Bellman

Trang 14