Lý thuyết đồ thị - Phần 4 docx

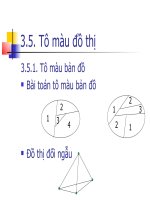
3.4. Đồ thị phẳng
3.4.1. Định nghiã và ví dụ

Biểu diễn phẳng

Đồ thị phẳng

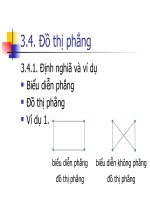
Ví dụ 1.
biểu diễn phẳng
đồ thị phẳng
biểu diễn không phẳng
đồ thị phẳng

3.4. Đồ thị phẳng

Ví dụ 2.

Ví dụ 3.

3.4. Đồ thị phẳng
3.4.2. Định lý Euler và các hệ quả

Định lý Euler:
Số miền phẳng=số cạnh-số đỉnh+2

Hệ quả 1:
Nếu G=(V,E) là đơn đồ thị phẳng, liên thông có m đỉnh
(m≥3) và n cạnh. Khi đó m ≤ 3n-6
Ví dụ 4: Chứng minh K
5

không phẳng

Hệ quả 2:
Nếu G=(V,E) là đơn đồ thị phẳng, liên thông có m đỉnh
(m≥3) và n cạnh, không có chu trình độ dài 3. Khi đó
m ≤ 2n-4
Ví dụ 5: Chứng minh K
3,3
không phẳng

3.4. Đồ thị phẳng
3.4.2. Đồ thị đồng phôi và
định lý Kuratovski

Phép phân chia sơ cấp

Từ một đồ thị phẳng G=(V,E), nếu
bỏ đi một cạnh và thêm vào một
đỉnh cùng với hai cạnh nối đỉnh vừa
thêm với các đỉnh kề của cạnh vừa
bỏ đi thi ta nói đã thực hiện một
phép phân chia sơ cấp đồ thị G.

Đồ thị đồng phôi

Hai đồ thị G
1
và G
2
được gọi là đồng

phôi nếu chúng cùng thu được từ
một đồ thị bằng một số hữu hạn các
phép phân chia sơ cấp.

3.4. Đồ thị phẳng

Định lý Kuratovski
Một đồ thị không phẳng khi và chỉ khi nó
chứa một đồ thị con đồng phôi với K
3,3
hoặc
K
5
.

Ví dụ:

Đồ thị Petersen

Đồ thị K
n
phẳng khi nào?

Đồ thị Q
n
phẳng khi nào?