Giáo trình thăm dò địa chấn trong địa chất dầu khí Chương 2 Cơ sở của phương pháp thăm dò địa chấn

Mai Thanh Tân

Chơng 2
cơ sở của phơng pháp thăm dò địa chấn
Phơng pháp địa chấn đợc tiến hành trên cơ sở nghiên cứu quá trình
truyền sóng đàn hồi trong môi trờng địa chất. Chính vì vậy, để hiểu rõ khả
năng áp dụng của phơng pháp, cần làm sáng tỏ các khái niệm cơ bản về
sóng đàn hồi, đặc điểm địa chất trong quá trình truyền sóng và cơ sở của
phơng pháp.
2.1. Cơ sở của phơng pháp địa chấn.

2.1.1. Sự hình thành sóng đàn hồi.
+ Cơ sở lý thuyết đàn hồi.
Trong thăm dò địa chấn, khi phát sóng ở một điểm nào đó thì sẽ làm
cho môi trờng xung quanh bị rung động. Vì lực kích thích nhỏ và thời gian
tác động rất ngắn nên có thể coi môi trờng địa chất là môi trờng đàn hồi,
các dao động đợc lan truyền dới dạng sóng đàn hồi. Trên cơ sở nh vậy,
những khái niệm về lý thuyết đàn hồi đợc sử dụng để nghiên cứu quá trình
truyền sóng.
Các vật thể đợc coi là đàn hồi nếu khi có lực tác dụng thì hình dạng
vật thể bị thay đổi và khi lực ngừng tác dụng thì vật thể trở lại trạng thái ban
đầu. Sự thay đổi hình dạng nh vậy gọi là sự biến dạng đàn hồi. Có thể phân
chia sự biến dạng đàn hồi thành hai loại: biến dạng thể tích và biến dạng hình
dạng. Nếu lực tác dụng chỉ làm thay đổi thể tích của vật thể còn hình dạng vẫn
giữ nguyên thì gọi là biến dạng thể tích. Ngợc lại nếu vật thể chỉ thay đổi
hình dạng và không thay đổi thể tích thì đó là biến dạng hình dạng. Các loại
biến dạng đàn hồi phức tạp đều đợc coi là tổng của biến dạng thể tích và biến
dạng hình dạng. Đối với chất rắn, khi bị lực tác dụng thì xảy ra cả biến dạng
thể tích và biến dạng hình dạng, còn với chất lỏng và chất khí thì chỉ xảy ra
biến dạng thể tích.
Khi có lực tác dụng vào vật thể gây nên sự biến dạng thì bên trong vật

thể đồng thời xuất hiện nội lực có xu hớng chống lại ngoại lực nhằm kéo các
phần tử vật chất về trạng thái ban đầu gọi là ứng lực. ứng lực tác dụng lên một
đơn vị diện tích nhằm cân bằng với ngoại lực gọi là ứng suất.
Mối quan hệ giữa ứng suất và biến dạng đợc xác định bởi những qui
luật nhất định. Nếu mối quan hệ này tuyến tính thì môi trờng nghiên cứu
đợc coi là môi trờng đàn hồi tuyệt đối, mối quan hệ giữa ứng suất và biến
dạng đợc mô tả bởi định luật Hooke.
Để làm sáng tỏ điều này, chúng ta có thể xét một thí dụ minh hoạ đơn
giản trên hình 2.1. Giả sử có một vật thể đàn hồi có hình trụ tròn có chiều dài l
14


Thăm dò địa chấn trong địa chất dầu khí

và đờng kính d bị gắn chặt một đầu. Dới tác dụng của lực F vật thể bị biến
dạng, có độ dãn dọc là l và độ nén ngang là d. Gọi độ dãn dọc tơng đối là
l = l/l và độ nén ngang tơng đối là d= d/d.
ứng suất T có độ lớn là:
d - d

d

F
F
T= =
S 4d 2

Vật thể đàn hồi đợc đặc
trng bởi các tham số đàn hồi nh
mô đun dãn dọc E (mô đun Young),

mô đun nén ngang (hệ số Poisson)
hoặc hằng số Lame à, và mật độ
.
Vì mối quan hệ giữa ứng suất
và biến dạng là tuyến tính nên ta có:
a
1
l = aT , l = T = T
l
E

l
l+l

a

b
F
F

Hình 2.1. Sự biến dạng của vật thể
hình trụ trớc khi lực tác dụng (a)
và sau khi lực tác dụng (b)

b
d

và d = bT, d = T .
ở đây a và b là hệ số tỷ lệ phụ thuộc vào tính chất đàn hồi và kích thớc
của vật thể:

d b l
=
=
l d a

E là mô đun dãn dọc (mô dun Young) và là mô dun nén ngang (hệ số
Poisson).
Mô dun Young có trị số bằng ứng suất khi vật thể bị dãn gấp 2 lần.
Các đại lợng E và đặc trng cho tính chất đàn hồi của vật thể và không
phụ thuộc vào nhau. Trên bảng 2.1 dẫn ra giá trị E và của một số loại đất
đá khác nhau.
Bảng 2.1
Đất đá

E (10-11 CGS)

Granit
Quaczit
Đá vôi

3-5
5-8
2.5 - 6



Đất đá

0.25 - 0.30 đá phiến

0.22 - 0.27 cát kết
0.22 - 0.35

E (10 11 CGS)
1.5 - 4.5
1.5 - 3.0



0.3 - 0.40
0.2 - 0.35

+ Sự hình thành sóng đàn hồi.
Trong thăm dò địa chấn, khi kích thích dao động thì sẽ gây nên sự
biến dạng và xuất hiện ứng suất có xu hớng kéo vật thể trở về trạng thái
ban đầu. Do hiện tợng quán tính nên các phần tử vật chất của môi trờng
15


Mai Thanh Tân

sẽ dao động quanh vị trí cân bằng. Các dao động này đợc lan truyền trong
môi trờng dới dạng sóng đàn hồi. Sóng đàn hồi đợc truyền đi với tốc độ
phụ thuộc vào các tham số đàn hồi của môi trờng. Trong môi trờng đồng
nhất, khi có sự kích thích dao động thì sẽ tạo ra hai loại sóng khác nhau là
sóng dọc (P) và sóng ngang (S).
Sóng dọc (P) liên quan đến biến dạng thể tích, các hạt vật chất dao
động trùng với phơng truyền sóng. Khi sóng dọc truyền đi sẽ tạo ra các
đới nén, dãn liên tiếp (hình 2.2a). Sóng ngang (S) liên quan đến biến dạng
hình dạng, các hạt vật chất dao động thẳng góc với phơng truyền sóng.

Khi sóng ngang truyền đi sẽ tạo ra các đới trợt liên tiếp (hình 2.2b).

a
b
Hình 2.2. Quá trình truyền sóng dọc (a) và sóng ngang (b)
Sóng dọc và sóng ngang truyền độc lập với nhau và có tốc độ là vP và vS

vP =

E(1 )
E
, vS =
(1+ )(1 2)
2 (1 + )

ở đây là mật độ đất đá, E là mô dun Young và là hệ số Poisson
So sánh giữa vP và vS ta có:

vP
2(1 )
=
> 2
vS
(1 2)

Nếu xác định đợc vP và vS thì có thể xác định đợc hệ số Poisson
đặc trng cho tính chất đàn hồi của đất đá.
2

2

1 v P 2vS
=
2 v P 2 vS 2

16


Thăm dò địa chấn trong địa chất dầu khí

Trong không khí và nớc, do không có biến dạng hình dạng nên chỉ
có sóng dọc mà không có sóng ngang. Trong thăm dò địa chấn biển, cáp
thu đợc bố trí trong nớc biển ở độ sâu 6-8m tính từ mặt nớc nên chỉ thu
đợc sóng dọc, để thu đợc sóng ngang cần đa cáp thu xuống sát đáy biển.
Trong địa chấn, việc quan sát sóng đợc tiến hành bằng cách ghi dao
động theo thời gian tại các điểm quan sát khác nhau trên tuyến. Nếu xét sự
dịch chuyển của dao động theo tia sóng tại một thời điểm nhất định thì đồ thị
biểu diễn dao động tại một thời điểm theo khoảng cách đợc gọi là tuyến
sóng. Khoảng cách giữa các cực trị cùng tên là bớc sóng (hình 2.3a).
Đồ thị biểu diễn dao động tại một điểm quan sát theo thời gian gọi là
hình dạng sóng. Độ lệch cực đại của đờng ghi so với vị trí cân bằng gọi là
biên độ (A), khoảng thời gian giữa hai cực trị cùng tên gọi là chu kỳ (T), đại
lợng nghịch đảo với chu kỳ xác định số dao động trong một đơn vị thời
gian gọi là tần số f = 1/T. Có thể sử dụng khái niệm tần số vòng = 2f
(hình 2.3b). Mối quan hệ giữa bớc sóng và chu kỳ đợc xác định bởi công
thức = vT. Trong đó v là tốc độ truyền sóng.
u

u

a

b

Hình 2.3. Tuyến sóng (a) và hình dạng sóng (b)
2.1.2. Cơ sở địa chấn hình học.
Trong quá trình nghiên cứu sự truyền sóng địa chấn có thể xét trờng
sóng theo các đặc điểm động hình học hoặc đặc điểm động lực.
Khi xét sự truyền sóng đàn hồi tơng tự nh các tia sáng trong quang
học, chúng ta quan tâm đến các đặc điểm động hình học của sóng nh trờng
thời gian, sự phân bố mặt sóng, thời gian truyền sóng, tốc độ... Việc nghiên
cứu chúng dựa trên cơ sở địa chấn hình học.
Khi nghiên cứu các đặc điểm động lực của trờng sóng cần xét các
tham số nh hình dạng sóng, biên độ, phổ tần số.
+ Trờng thời gian.
Khi phát sóng tại một điểm nào đó thì sẽ tạo ra sóng đàn hồi truyền
trong môi trờng. Trong quá trình truyền sóng, có thể xác định đợc thời gian
17


Mai Thanh Tân

sóng truyền đến các điểm có toạ độ khác nhau. Khoảng không gian tồn tại mối
quan hệ giữa thời gian truyền sóng và toạ độ điểm quan sát gọi là trờng thời
gian. Trờng thời gian đợc đặc trng bởi mặt sóng và tia sóng. Mặt sóng là
các mặt mà trên đó thời gian sóng đến nh nhau, còn đợc gọi là mặt đẳng
thời. Khi nghiên cứu tập hợp các mặt đẳng thời có thể xác định đặc điểm
truyền sóng. Tia sóng là những đờng thẳng góc với mặt đẳng thời và trùng
với phơng truyền sóng. Trong môi trờng đồng nhất, tia sóng là đờng
thẳng còn trong môi trờng không đồng nhất do tốc độ truyền sóng thay đổi

nên tia sóng có thể là đờng cong, đờng gấp khúc.
Khi tiến hành phơng pháp địa chấn, với một nguồn phát thờng thu
sóng tại nhiều điểm khác nhau trên các tuyến quan sát. Mối quan hệ giữa
thời gian sóng đến và toạ độ điểm quan sát đợc biểu diễn bởi các biểu đồ
thời khoảng (BĐTK). Khi quan sát trên từng tuyến (địa chấn 2D) biểu đồ
thời khoảng là những đờng thẳng hoặc đờng cong, khi quan sát trên diện
tích gồm nhiều tuyến khác nhau (địa chấn 3D), biểu đồ thời khoảng là các
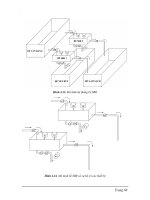
mặt. Một vài thí dụ biểu đồ thời khoảng sóng phản xạ và sóng khúc xạ đợc
thể hiện trên các hình 2.12 - 2.15 và các hình 8.2 - 8.4
Các loại sóng đàn hồi trong môi trờng thờng đến máy thu theo các
hớng truyền sóng khác nhau, vì vậy t
có sự chênh lệch thời gian sóng đến
tại các điểm trên tuyến quan sát. t2
t
Nếu tính tốc độ không phải theo
phơng truyền sóng mà tính dọc t1
x
theo tuyến quan sát thì đó là tốc độ
A
B
0
biểu kiến (v*).
x

Chúng ta xét thí dụ trên hình
C
2.4. Giả sử tia sóng đến tạo với
tuyến quan sát góc . Thời gian
z
sóng đến tại 2 điểm A và B là t1 và

t2. Sự chênh lệch thời gian sóng đến Hình 2.4. Cách tính tốc độ biểu kiến
giữa A và B là t2 - t1 = t.
Tốc độ truyền sóng dọc theo tia là: v = CB/ t
Nếu tính tốc độ theo tuyến quan sát, ta có
v* =

tốc độ biểu kiến

AB
. Mối quan hệ giữa tốc độ biểu kiến v* và tốc độ v theo tia đợc
t 2 t1

xác định theo công thức:

v* =

v
sin

18


Thăm dò địa chấn trong địa chất dầu khí

Nh vậy, tốc độ biểu kiến sẽ thay đổi tuỳ theo hớng sóng đến. Khi
sóng truyền dọc theo tuyến quan sát thì tốc độ biểu kiến có giá trị nhỏ
nhất và chính bằng tốc độ sóng truyền theo tia. Khi tia sóng đến nghiêng
so với tuyến quan sát thì v*> v. Khi sóng đến thẳng góc với mặt ranh giới
( = 0) thì mặt sóng trùng với mặt quan sát, sóng đến các điểm trên tuyến
quan sát cùng một lúc, lúc đó v* = . Khái niệm tốc độ biểu kiến đợc sử

dụng trong xử lý số liệu để xác định sự khác biệt của các sóng có hớng
sóng đến khác nhau, điều này cho phép loại trừ các loại nhiễu có hớng
sóng đến khác với sóng có ích.
+ Các định luật cơ bản của địa chấn hình học
Để nghiên cứu các đặc điểm động hình học của trờng sóng địa chấn
cần áp dụng các nguyên lý trong quang học nh nguyên lý HuyghenFresnel, nguyên lý Fermat,.
Theo nguyên lý Huyghen Fresnel, trong quá trình truyền sóng, mỗi
điểm của môi trờng nằm trên mặt sóng có thể coi là nguồn phát sóng thứ cấp.
Nhờ nguyên lý này, có thể xác định đợc đặc điểm quá trình truyền sóng trong
môi trờng, nói cách khác là xác định đợc vị trí mặt sóng ở một thời điểm bất
kỳ nếu biết mặt sóng ở một thời điểm nhất định.
Theo nguyên lý Fermat,, thời gian sóng truyền theo tia sóng là ngắn
nhất so với thời gian sóng truyền theo bất kỳ phơng nào khác. Xét thời
gian sóng truyền theo tia ds giữa 2 điểm A và B với tốc độ v(x,y,z), ta có:

t=

ds

v(x, y, z) = min

AB

Trên cơ sở nguyên lý Fermat,, có thể xác định dạng tia sóng trong
môi trờng nếu biết qui luật phân bố tốc độ
2.1.3. Sự phản xạ, khúc xạ và tán xạ sóng đàn hồi.
Trong quá trình truyền sóng đàn hồi, nếu gặp các mặt ranh giới phân
chia 2 môi trờng có tính chất đàn hồi khác nhau thì sẽ xuât hiện sóng phản
xạ và sóng qua. Chúng ta xét trờng hợp đơn giản khi môi trờng có mặt
ranh giới phẳng nằm ngang R phân chia thành 2 phần đợc đặc trng bởi

các tham số khác nhau, đó là tốc độ sóng dọc vP1,vP2, tốc độ sóng ngang vS1,
vS2 và mật độ 1, 2 (hình 2.5)
Mối quan hệ giữa sóng tới và các sóng thứ cấp đợc xác định bởi
định luật khúc xạ:

vS1
vS 2
vP1
vP1
vP 2
=
=
=
=
sin
sin P
sin S
sin P
sin S

19


Mai Thanh Tân

Đối với sóng phản xạ dọc (cùng loại) P11, do có cùng tốc độ với sóng tới
nên góc tới bằng góc phản xạ = P.
Giả sử có sóng tới là sóng dọc P1, khi đạt tới mặt ranh giới sẽ tạo ra các
sóng thứ cấp. Một phần năng lợng tạo nên các sóng quay trở về môi trờng
phía trên, đó là sóng phản xạ dọc P11 (cùng loại với sóng tới) và sóng phản xạ

biến loại P1S1 (khác loại với sóng tới). Một phần năng lợng truyền qua mặt
ranh giới tạo nên sóng qua, đó là sóng cùng loại P12 và sóng biến loại P1S2.
t
Góc hợp bởi tia sóng và
pháp tuyến mặt ranh giới ở phía
trên là và phần môi trờng
p1
p1s1
phía dới là .
p11
Khả năng phản xạ của
sóng trên mặt ranh giới R đợc
p
đặc trng bởi hệ số phản xạ K. vp1,vs1, 1
x
Đó là tỉ số giữa biên độ sóng
vp2, vs2, 2
p
phản xạ Ap11, Ap1s1với biên độ
sóng tới Ap1.
P12
Các kết quả tính toán đã
P1S2
z
chỉ ra rằng, khi tia sóng đổ
thẳng góc với mặt ranh giới sẽ Hình 2.5. Sự hình thành sóng phản xạ
và sóng qua
không có sóng phản xạ biến
loại và hệ số phản xạ là:

R0 =

AP11
AP1

=

v P 22 v P11
v P22 + v P11

Tích số I = v đợc gọi là trở sóng âm học. Nh vậy, để có sóng
phản xạ thì mặt ranh giới cần thoả mãn điều kiện: v22 v11. Tuỳ vào mối
quan hệ giữa v11 và v22 mà hệ số phản xạ có thể mang dấu (-) hoặc dấu
(+) và luôn nhỏ hơn 1.
Khi quan sát xa nguồn phát, sóng không đổ vuông góc xuống mặt
ranh giới (góc 0) thì hệ số phản xạ không còn là hằng số nữa mà sẽ có
sự biến đổi phức tạp phụ thuộc vào khoảng cách thu nổ (hoặc phụ thuộc vào
góc đổ). Theo một số tính toán cho thấy:
R() = R0 + G sin2
Trong đó R0 là hệ số phản xạ khi góc đổ = 0, G là hệ số phụ thuộc
vào tính chất đàn hồi của môi trờng.
Sự biến đổi này liên quan không chỉ trở sóng âm học I mà cả hệ số
Poisson của đất đá ở mặt ranh giới. Đây là cơ sở của phơng pháp nghiên
20


Thăm dò địa chấn trong địa chất dầu khí

cứu sự biến đổi biên độ theo khoảng cách thu nổ (Amplitude Vesus Offset,
viết tắt là AVO), đợc áp dụng để xác định các tầng chứa dầu khí.

Khi sóng tới đạt đến mặt ranh giới R, ngoài phần năng lợng tạo nên
sóng phản xạ quay trở lại môi trờng phía trên thì một phần năng lợng sẽ tạo
nên đi xuyên qua môi trờng phía dới. Hệ số sóng qua là Q, đợc xác định
A
2v P11
QPP = PP =
theo công thức:
A P1 v P22 + v P11
Theo định luật Snell ta có:

v1
v
= 2
sin sin

Trong trờng hợp v2 > v1 thì > , khi quan sát càng xa điểm nổ,
góc đổ tăng dần và có thể đạt đến góc tới hạn i khi góc đạt 900. Ta có:
v
sin i = 1
v2
Khi đó sóng qua trợt dọc
0
theo mặt ranh giới R trong môi
P1
trờng thứ 2. Đây là hiện tợng
phản xạ toàn phần. Sóng trợt
P121
theo mặt ranh giới sẽ kích thích

i

v1
môi trờng phía trên, theo
nguyên lý Huyghen nó sẽ tạo
P12
v2

nên sóng thứ cấp P121 quay trở
về bề mặt. Sóng P121 đợc gọi là
P12
sóng khúc xạ. Do có quãng
đờng truyền sóng với tốc độ
v2 > v1 nên thờng sóng này Hình 2.6. Sự hình thành sóng khúc xạ
đến máy thu trớc so với các
sóng khác, ngời ta còn gọi đây là sóng đầu (hình 2.6).
Điều kiện để có sóng khúc xạ là phải có mặt ranh giới thoả mãn điều
kiện tốc độ lớp dới lớn hơn tốc độ lớp trên (v2 > v1). Sóng khúc xạ chỉ quan
sát đợc cách xa nguồn một khoảng cách nhất định, khoảng cách này phụ
thuộc vào chiều sâu của mặt ranh giới và quan hệ v2 / v1.
Ngoài các sóng phản xạ và khúc xạ đợc hình thành từ các mặt ranh
giới nh đã nêu, trong môi trờng bất đồng nhất còn có sóng tán xạ. Sóng
tán xạ đợc hình thành do sóng tới tác động vào đối tợng có tham số đàn
hồi khác với môi trờng xung quanh nhng kích thớc nhỏ so với bớc sóng.
Sự có mặt của các đới phá huỷ kiến tạo, đứt gãy, vát nhọn địa tầng, địa hình
lồi lõm của mặt đá móng... làm xuất hiện sóng tán xạ.

21


Mai Thanh Tân

đờng cong tán xạ
ô tán xạ

Hình 2.7. Sóng tán xạ từ mép đứt gãy
Đờng cong tán xạ (a) và ô tán xạ trên lát cắt (b)

Sự xuất hiện sóng tán xạ trên lát cắt địa chấn dễ dẫn đến phân tích sai
lệch hình ảnh thực của môi trờng. Trong những trờng hợp nh các đới nứt
nẻ chứa dầu khí trong móng granit ở thềm lục địa Việt Nam thì sự xuất hiện
trờng sóng tán xạ từ các đới nứt nẻ, phá huỷ trở thành đối tợng nghiên
cứu chủ yếu. Điều này đòi hỏi phải có hệ thống xử lý tài liệu đặc biệt hơn
so với các phơng pháp truyền thống.
2.2. Trờng sóng địa chấn trong môi trờng địa chất

Quá trình truyền sóng trong môi trờng địa chất chịu ảnh hởng của
nhiều yếu tố nên rất phức tạp, tốc độ truyền sóng thay đổi với các loại đất
đá khác nhau, ngoài sóng có ích còn tồn tại rất nhiều loại sóng nhiễu...
Chính vì vậy cần tìm hiểu kỹ đặc điểm của các yếu tố địa chất để áp dụng
phơng pháp địa chấn có hiệu quả.
2.2.1. Sóng địa chấn trong môi trờng phân lớp
Trong các bể trầm tích, môi trờng địa chất thể hiện tính phân lớp rõ
rệt và bề dày các lớp thay đổi rất khác nhau. Trong thăm dò địa chấn, bề
dày các lớp đợc so sánh tơng đối so với bớc sóng và thờng chỉ phát
hiện đợc các lớp có bề dày không nhỏ hơn 1/4 bớc sóng. Thí dụ với sóng
có bớc sóng = 60m (f = 40Hz, v = 3000m/s), thì có thể xác định lớp có
bề dày khoảng 18m.
Trong môi trờng trầm tích phân lớp, tồn tại nhiều loại sóng khác
nhau. Trớc hết xét trờng hợp đơn giản là trong môi trờng chỉ có một
lớp dày với các tham số vP1,vS1,1 nằm trên nửa không gian có tham số
vP2,vS2,2 (hình 2.8). Khi nguồn phát sóng đặt trong lớp đàn hồi ở độ sâu h0

chúng sẽ tạo ra nhiều loại sóng khác nhau trong lớp đàn hồi này.
- Sóng phản xạ và sóng qua: Khi sóng P1 từ nguồn đến mặt ranh giới
sẽ tạo ra các sóng phản xạ quay trở lại mặt quan sát và sóng qua đi vào môi
trờng phía dới. Các sóng thứ cấp này có thể cùng loại P11, P12 hoặc biến
loại P1S1, P1S2. (hình 2.8a).
22


Thăm dò địa chấn trong địa chất dầu khí

- Sóng khúc xạ: Nếu vP2 > vP1 thì có hiện tợng phản xạ toàn phần,
sóng qua P12 trợt theo mặt ranh giới và tạo nên sóng khúc xạ quay trở về
mặt quan sát (P121, P12S1). Nếu tốc độ truyền sóng trong lớp đàn hồi quá nhỏ
để vS2 > vP1 thì còn tạo ra các sóng đầu P1S21, P1S2P1 (hình 2.8c)
- Sóng phản xạ nhiều lần (PXNL): Là loại sóng bị phản xạ nhiều
lần trong các mặt ranh giới khác nhau trong môi trờng trớc khi tới máy
thu. Sự tồn tại của sóng PXNL rất nguy hiểm và gây nhầm lẫn khi xác
định các mặt phản xạ thực có trên lát cắt. Do sóng PXNL cũng là sóng
phản xạ nên việc nhận dạng chúng và áp dụng các biện pháp triệt tiêu
chúng rất phức tạp.
- Sóng kèm: Ngoài sóng P1 từ nguồn đi xuống mặt ranh giới phía
dới còn có tia sóng P1 đi lên mặt ranh giới phía trên sau đó bị phản xạ
quay xuống, sóng này kèm sau sóng phản xạ nên gọi là sóng kèm (hay còn
gọi là sóng vệ tinh) P111, P11S1 (hình 2.8b,e)
a

d

c

b

e

g

Hình 2.8. Các loại sóng trong một lớp dày
- Sóng phản xạ - khúc xạ, sóng khúc xạ - phản xạ: Khi vP2 > vP1 thì có
thể xảy ra sóng phản xạ - khúc xạ hoặc sóng khúc xạ - phản xạ (hình 2.8c,d,g)
- Sóng mặt: Ngoài các sóng nêu trên gọi chung là sóng khối, ở các
mặt ranh giới còn xuất hiện các loại sóng mặt nh sóng Rayleigh, Love
Sóng Rayleigh liên quan đến mặt đất - không khí, các hạt môi trờng
chuyển động theo quĩ đạo hình elíp trong mặt phẳng thẳng góc với mặt ranh
giới, tốc độ truyền sóng vR 0,9 vS. Sóng Love xuất hiện ở các mặt ranh
giới có vi > vi-1 và nằm trong mặt ranh giới.
- Sóng tán xạ : Sóng tán xạ xuất hiện khi trong môi trờng có các đối
tợng có kích thớc nhỏ so với bớc sóng. Vì kích thớc của đối tợng nhỏ

23


Mai Thanh Tân

nên có thể coi nh một nguồn điểm thứ cấp và làm xuất hiện dao động phát
triển về mọi phía của môi trờng.
Nếu trong môi trờng có nhiều lớp thì số lợng mặt ranh giới tăng lên,
số lợng các sóng thứ sinh cũng tăng lên gấp bội và trờng sóng trở nên rất
phức tạp. Việc phát hiện các loại sóng nhiễu và tìm các biện pháp hạn chế
chúng là một trong những nhiệm vụ rất quan trọng.
2.2.2. Mô hình địa chấn - địa chất

Trong quá trình truyền sóng từ nguồn phát đến máy thu, do ảnh
hởng của nhiều yếu tố khác nhau mà hình dạng, biên độ, phổ tần số của
xung sóng địa chấn có sự biến đổi. Các yếu tố đó là sự mở rộng mặt sóng,
sự phản xạ và khúc xạ trên các mặt ranh giới trung gian và sự hấp thụ năng
lợng. Sự biến đổi dạng xung phụ thuộc rất nhiều vào cấu trúc của tập hợp
các lớp có bề dày, tốc độ và mật độ khác nhau. Hình ảnh các yếu tố tác
động lên đặc điểm trờng sóng đợc minh họa trên hình 2.9.

Hình 2.9. Các yếu tố ảnh hởng đến dạng sóng địa chấn
trong quá trình truyền sóng.
ở những vùng đã có tài liệu địa chất (nh cột địa tầng giếng khoan, tài
liệu thạch học...), có thể xây dựng mô hình trờng sóng địa chấn. Đây là
dạng mô hình thuận, nghĩa là xác định các đờng ghi địa chấn từ tài liệu
địa chất đã có. Dạng mô hình này khác với mô hình ngợc là xác định mô
hình địa chất (thể hiện qua lát cắt trở sóng âm học) từ lát cắt địa chấn. Một
dạng mô hình thuận đợc sử dụng phổ biến trong thăm dò địa chấn là xây
dựng băng địa chấn lý thuyết, hay còn gọi là băng địa chấn tổng hợp
(synthetic seismogram). Quá trình hình thành băng địa chất tổng hợp và so
sánh với băng địa chấn thực tế đợc trình bày trên hình 2.10 và 2.11.
24


Thăm dò địa chấn trong địa chất dầu khí

b

c

d

e

g

thời gian

chiều sâu

a

Hình 2.10. Nguyên tắc xây dựng mô hình băng địa chấn tổng hợp.
a. Cột địa tầng, b. Trở sóng âm học, c. Hệ số phản xạ (theo chiều sâu), d. Hệ số phản
xạ (theo thời gian), e. Dạng xung sóng địa chấn, g. Dạng đờng ghi địa chấn

a

b

c

Hình 2.11. So sánh băng địa chấn tổng hợp và băng địa chấn thực tế.
a. Quá trình so sánh băng địa chấn tổng hợp và băng địa chấn thực tế.
b. Băng địa chấn tổng hợp, c. Băng địa chấn thực tế

25


Mai Thanh Tân

Từ cột địa tầng ở các giếng khoan, có thể xác định giá trị tốc độ và

mật độ của các lớp đất đá. Từ đó tính giá trị trở sóng âm học (I = v) của
các lớp và hệ số phản xạ của các mặt ranh giới theo chiều sâu. Trên cơ sở
mối quan hệ giữa độ sâu và thời gian truyền sóng (đợc xác định theo kết
quả đo địa chấn trong giếng khoan), có thể chuyển sự phân bố hệ số phản
xạ theo chiều sâu sang phân bố theo thời gian truyền sóng. Sự phân bố hệ
số phản xạ theo thời gian đợc gọi là băng xung, nếu tích chập băng
xung này với dạng xung địa chấn khi phát sóng thì kết quả sẽ hình thành
đờng ghi địa chấn. Tập hợp các đờng ghi địa chấn tạo thành băng địa
chấn tổng hợp. Trong thực tế có thể xây dựng băng địa chấn tổng hợp với
mô hình sóng phản xạ (có ích) hoặc mô hình sóng nhiễu để so sánh với
băng địa chấn thực tế. Việc so sánh băng địa chấn tổng hợp với băng địa
chấn thực tế cho phép xác định sóng có ích và sự sự tồn tại của các loại
nhiễu. Sự sai khác giữa chúng cho phép điều chỉnh mô hình và nâng cao
hiệu quả xử lý số liệu.
2.3. tốc độ sóng địa chấn

Tốc độ truyền sóng địa chấn là một tham số vật lý rất quan trọng
cung cấp nhiều thông tin hữu ích trong phân tích tài liệu địa chấn
2.3.1. Tốc độ truyền sóng của đất đá.
Tốc độ truyền sóng trong môi trờng địa chất có sự biến đổi phức
tạp tuỳ thuộc vào thành phần thạch học của đất đá và nhiều yếu tố khác.
Để xác định tốc độ truyền sóng trong các loại đất đá khác nhau cần tiến
hành đo siêu âm mẫu đất đá trong phòng thí nghiệm hoặc đo siêu âm
giếng khoan.
Các loại đất đá khác nhau trong quả đất có tốc độ truyền sóng khác
nhau. Các lớp đất trồng ở sát mặt đất có tốc độ khoảng 300 - 400 m/s, trong
khi đó đá macma và một số đá trầm tích tốc độ truyền sóng có thể đạt tới
6000 - 7000m/s. Theo tài liệu đo sâu địa chấn thì các đá nằm ở chiều sâu
vài chục km có thể tốc độ lớn hơn 8000 m/s.
Sự khác biệt về tốc độ truyền sóng của đất đá phụ thuộc vào thành phần

thạch học, điều kiện thành tạo, chiều sâu thế nằm, độ rỗng, độ ngậm nớc.
- Thành phần thạch học: Thành phần thạch học là yếu tố ảnh hởng
quyết định tới tốc độ truyền sóng của đất đá. Các đá macma và đá biến chất
có tốc độ thay đổi từ 4000 - 6500m/s. Các đá trầm tích có tốc độ nhỏ hơn so
với đá macma và đá biến chất, trong đó đá trầm tích lục nguyên có tốc độ
nhỏ, ít khi vợt quá 4000m/s. Các đá trầm tích thuỷ hoá và cacbonat có tốc
độ xấp xỉ so với đá macma và đá biến chất.
Trong bảng 2.2 nêu một số thí dụ về tốc độ một số loại đất đá

26


Thăm dò địa chấn trong địa chất dầu khí

Bảng 2.2
Loại đá
Đất đá bở rời
Cát (khô)
Cát (bão hoà nớc)
Sét
Đá trầm tích
Cát kết
Cát kết Đệ tam
Cacbonat
Quarzit
Đá vôi
Đá vôi cacbonat
Dolomit

Tốc độ

(km/s)

0.2 -1.0
1.5- 2.0
1.5 2.5
2.0 6.0
2.0 2.5
4.0 4.5
5.5 6.0
2.0- 6.0
5.0 5.5
2.5 6.5

Loại đá

Muối mỏ
Anhydrit
Thạch cao
Đá macma/ biến chất
Granit
Gabro
Siêu mafic
Serpentin
Khí và chất lỏng
Khí
Nớc
Dầu

Tốc độ
(km/s)

4.5 -5.0
4.5 6.5
2.0 3.5

5.5 6.0
6.5 7.0
7.5 8.5
5.5 6.5
0.3
1.4 1.5
1.3 - 1.4

Đối với các loại đá có cùng thành phần thạch học, giá trị tốc độ có
thay đổi phụ thuộc vào áp suất, độ rỗng, độ ngậm nớc...
- áp suất: Khi tăng áp suất sẽ làm giảm độ rỗng và tăng mô đun đàn
hồi, dẫn đến làm tăng tốc độ truyền sóng. Sự phụ thuộc của tốc độ vào áp
suất thể hiện rõ nét ở các trầm tích lục nguyên và hầu nh không thể hiện ở
đá macma và đá cacbonat.
- Độ rỗng: Khi độ rỗng tăng thì tốc độ truyền sóng giảm. Các đới
phong hoá bở rời ở sát mặt đất tốc độ truyền sóng có thể nhỏ hơn tốc độ
truyền sóng âm trong không khí. Các khu vực bị phá huỷ kiến tạo, nứt nẻ...
tốc độ truyền sóng giảm hẳn so với ở các đá nguyên khối.
- Độ ngậm nớc và dầu: Với các đất đá có lỗ hổng chứa nớc thì khi
độ bão hoà nớc tăng lên, phần lỗ hổng chứa khí giảm xuống, mô đun
Young cũng tăng lên dẫn tới tăng tốc độ truyền sóng. Mức độ tăng tốc độ
truyền sóng có thể đạt tới vài chục phần trăm. Khi nớc trong các lỗ hổng
đợc thay bằng dầu thì tốc độ truyền sóng có thể giảm 10 ữ 15%, nếu thay
bằng khí thì tốc độ truyền sóng này còn giảm nhiều hơn, có thể đến 20 ữ
30%.
- Chiều sâu thế nằm: Khi chiều sâu tăng, áp suất thủy tĩnh tăng dẫn

đến tăng tốc độ truyền sóng. Mức độ tăng của tốc độ truyền sóng theo chiều
sâu phụ thuộc vào thành phần thạch học và độ rỗng của đá. Điều này thể
hiện rõ rệt đối với các đá lục nguyên bở rời có độ rỗng lớn.
- Tuổi của đất đá: Các loại đất đá có tuổi càng già thì tốc độ truyền
sóng cũng tăng lên, ở một số vùng ngời ta tìm ra qui luật

27


Mai Thanh Tân

vP = k (hT)1/6
Trong đó k là hệ số phụ thuộc thành phần thạch học, h là chiều
sâu, T là tuổi tuyệt đối. Sự tăng tốc độ truyền sóng theo tuổi của đất đá
liên quan đến tác dụng biến chất động lực và tác dụng kéo dài của các
dung dịch chứa trong đá.
Những vấn đề nêu trên liên quan đến cả tốc độ truyền sóng dọc và
sóng ngang. Trong đa số các loại đất đá, tỉ số vS/vP nằm trong khoảng 0,5 0,6. Với các đá ngậm nớc tỉ số này có thể giảm đến 0,1 - 0,2
Mối quan hệ giữa tốc độ vp trong các đá có độ rỗng chứa chất lỏng
đợc xác định bởi công thức:

1 1
=
+
vp
vm
vf
Trong đó vm, vf là tốc độ của khung đá và của chất lỏng, là độ
rỗng. Công thức này thờng đúng với các loại cát sạch, có độ rỗng 10 ữ
25%, khi độ rỗng giảm thì độ chính xác giảm đi.

Ngoài sự phụ thuộc vào chất lỏng trong lỗ hổng, ngời ta đã nghiên cứu
đợc mối quan hệ giữa tốc độ và hàm lợng sét. Khi hàm lợng sét tăng thì tốc
độ sóng dọc và sóng ngang giảm.

vp = 5,59 - 6,93 - 2,18 C
vs = 3,52 - 4,91 - 1,89 C
Trong đó C là tỷ lệ sét, là độ rỗng.
Tốc độ có mối quan hệ với áp suất, thờng tốc độ tăng khi tăng áp
suất. Đây cũng là dấu hiệu quan trọng khi nghiên cứu dị thờng áp suất, đặc
biệt trong thăm dò và khai thác các mỏ khí. Trong các đới nứt nẻ, tốc độ và
áp suất tăng khi mức độ nứt nẻ giảm. Theo hớng phát triển nứt nẻ và
hớng thẳng góc với chúng giá trị tốc độ có khác nhau, đó là tính bất định
hớng về tốc độ.
Sự tồn tại khí ở trong lỗ hổng làm giảm giá trị tốc độ. Với sự thay đổi
độ bão hoà khí vài phần trăm cũng đủ làm cho tốc độ giảm đi đáng kể.
Thờng các tầng chứa khí liên quan đến các điểm sáng trên lát cắt địa
chấn và có thể nhận biết một cách thuận lợi.
2.3.2. Các loại tốc độ đợc sử dụng trong thăm dò địa chấn
Trong thăm dò địa chấn, ngoài tốc độ thực của các loại đất đá khác
nhau nh đã nêu trên, để phục vụ cho các nhiệm vụ phân tích tài liệu địa
chấn, đặc biệt là chuyển từ lát cắt thời gian sang lát cắt chiều sâu trong môi
trờng địa chất phân lớp, có thể sử dụng nhiều loại tốc độ khác nhau nh

28


Thăm dò địa chấn trong địa chất dầu khí

tốc độ lớp (vl), tốc độ trung bình (vtb), tốc độ hiệu dụng (vhd), tốc độ điểm
sâu chung (vĐSC), tốc độ ranh giới (vrg), tốc độ biểu kiến (v*)...

- Tốc độ lớp (vl) là tốc độ trung bình của một lớp địa chấn (bao gồm
nhiều phân lớp mỏng), đợc tính theo tia vuông góc với mặt phân lớp:
n

h
vl = =
t

h k

K =1
n

t k

K =1

Trong đó h là chiều dày lớp địa chấn, t là thời gian truyền sóng
theo hớng vuông góc với mặt lớp, hk và tk là chiều dày và thời gian sóng
truyền trong phân lớp mỏng thứ k, n là số phân lớp mỏng.
- Tốc độ bình phơng trung bình: v rms =

v i2 t i
ti
i

- Tốc độ khoảng: là tốc độ trung bình trong một khoảng nhất định đợc
tính cho tia sóng vuông góc với mặt ranh giới. Tốc độ này còn có tên là tốc độ
Dix:

vi =

v 2n t n v 2n 1 t n 1
t n t n 1

Trong đó vn là tốc độ bình phơng trung bình và tn là thời gian tính
theo tia vuông góc tơng ứng với mặt ranh giơi n
- Tốc độ trung bình (vtb): là tốc độ truyền sóng trung bình đợc tính
cho toàn bộ phần môi trờng từ mặt đất tới chiều sâu xác định nào đó. Tốc
độ trung bình (vtb) đợc xác định theo công thức:
(vtb) = z / t(z)
Để xác định tốc độ lớp (vl) và tốc độ trung bình (vtb) cần phải tiến
hành đo và phân tích tài liệu đo địa chấn trong các giếng khoan. Cụ thể là
tiến hành nghiên cứu bằng phơng pháp địa chấn giếng khoan và tuyến địa
chấn thẳng đứng.
- Tốc độ hiệu dụng là tốc độ truyền sóng trong môi trờng lớp phủ
đợc xác định theo tài liệu địa chấn trên mặt với giả thiết lớp phủ đồng
nhất, mặt ranh giới phẳng và tuyến quan sát thẳng. Vì môi trờng thực tế
nói chung khác với mô hình lý thuyết nên tốc độ xác định đợc không trùng
với tốc độ trung bình. Tuy nhiên, tốc độ xác định đợc thờng không khác
nhiều (sai số không quá 5%) so với tốc độ trung bình xác định bằng địa
chấn giếng khoan nên tốc độ hiệu dụng đợc sử dụng rộng rãi vào các mục
29


Mai Thanh Tân

đích khác nhau của thăm dò địa chấn. Trong điều kiện khu vực nghiên cứu
cha có các giếng khoan sâu có thể sử dụng vhd thay thế một cách gần đúng
cho vị trí của vtb. Để xác định tốc độ hiệu dụng có thể sử dụng các BĐTK

sóng phản xạ quan sát đợc ở khu vực nghiên cứu.
- Tốc độ điểm sâu chung (vĐSC): là loại tốc độ đợc xác định theo
BĐTK điểm sâu chung:
vĐSC = v/cos
Trong đó là góc nghiêng của mặt ranh giới. vĐSC đợc tính bằng
phơng pháp quét tốc độ khi xử lý tài liệu địa chấn ĐSC.
- Tốc độ ranh giới (vrg): là tốc độ truyền sóng khúc xạ trợt phía dới
mặt ranh giới. Nếu môi trờng phía dới mặt khúc xạ là đồng nhất thì vrg
đặc trng cho cả môi trờng đó. Nếu môi trờng này không đồng nhất thì
vrg chỉ đặc trng cho lớp đất đá nằm gần mặt ranh giới, chính vì vây có tên
gọi là tốc độ ranh giới. Giá trị vrg không chỉ sử dụng để xây dựng mặt ranh
giới khúc xạ mà còn là cơ sở để suy luận tính chất thạch học đất đá của mặt
ranh giới khúc xạ.
- Tốc độ biểu kiến (v*): là tốc độ đợc xác định theo tuyến quan sát
mà không phải xác định theo phơng truyền sóng. Tuỳ theo hớng sóng
0
đến mà giá trị tốc độ biểu kiến thay đổi từ v* = v (khi góc đổ = 90 )
đến v* = (khi = 0).
2.4. Biểu đồ thời khoảng

Trong quá trình truyền sóng, có thể xác định đợc thời gian sóng đến
các điểm quan sát khác nhau. Đồ thị biểu diễn sự phụ thuộc thời gian
truyền sóng đến các điểm quan sát và toạ độ của các điểm quan sát đó đợc
gọi là biểu đồ thời khoảng (BĐTK).
Tuỳ thuộc vào cách bố trí các điểm quan sát mà có các loại BĐTK
khác nhau. Khi các điểm quan sát đợc bố trí trên những diện tích nhất định
ta có BĐTK mặt, khi quan sát theo tuyến ta có BĐTK đờng, khi quan sát
trong giếng khoan có BĐTK thẳng đứng. BĐTK mặt đợc biểu diễn trong hệ
toạ độ (t,x,y), BĐTK đờng biểu diễn trong hệ toạ độ (t,x), và BĐTK thẳng
đứng trong hệ toạ độ (t,h)

2.4.1. Biểu đồ thời khoảng sóng phản xạ
Để đơn giản, chúng ta xét BĐTK sóng phản xạ khi quan sát theo
tuyến. Giả sử trong môi trờng có mặt ranh giới phản xạ R nằm nghiêng
so với mặt quan sát một góc . Tốc độ truyền sóng phía trên mặt ranh giới
là v, độ sâu mặt ranh giới tại điểm nổ O theo hớng thẳng góc với mặt
ranh giới (độ sâu pháp tuyến) là h (hình 2.12).
30


Thăm dò địa chấn trong địa chất dầu khí

Sóng từ nguồn O đến mặt ranh giới R tạo nên các sóng phản xạ và có
thể quan sát chúng tại các điểm khác nhau theo tuyến Ox.
Các sóng phản xạ từ
nguồn nổ O tơng tự nh
sóng trực tiếp từ nguồn nổ ảo
O* đối xứng với nguồn nổ
thực qua mặt ranh giới R.
Thời gian truyền sóng
đến điểm quan sát S(x) đợc
xác định là :
OA + AS O*S
=
v
v
O là hình chiếu của O*
lên mặt quan sát, A là điểm
phản xạ trên mặt R
1
t=

O * O"2 + O"S 2 =
v
Hình 2.12. Biểu đồ thời khoảng sóng phản xạ
1
x 2 + 4 hx sin + 4 h 2
v
Tuỳ thuộc vào hớng nghiêng của mặt ranh giới mà góc có thể
có dấu (+) hoặc dấu (-). Thời gian sóng phản xạ thu đợc khi đặt máy thu
2h
.
tại điểm nổ là: t 0 =
v
t=

Thời gian cực tiểu của BĐTK: t m =

O * O" 2 h
=
cos
v
v

Khoảng cách dịch chuyển điểm cực tiểu về phía mặt ranh giới nâng
lên so với điểm nổ là: O*O= 2h sin.
Nếu chuyển gốc toạ độ từ điểm nổ O về vị trí O và ký hiệu
khoảng cách tính từ O là thì BĐTK có dạng:
t=

1
2

2 + Z0
v

Trong đó = x + 2hsin, Z0 = 2hcos
Phơng trình trên chỉ ra rằng BĐTK của sóng phản xạ là đờng
hyperbol đối xứng qua trục của hệ toạ độ có gốc ở O.
Trong trờng hợp ranh giới nằm ngang = 0, phơng trình BĐTK
sóng phản xạ trở nên đơn giản:
1 2
t=
x + 4h 2
v
31


Mai Thanh Tân

Khi đó điểm cực tiểu của hyperbol nằm trên trục toạ độ qua
điểm nổ và t 0 = tmin.
Khi trong môi trờng có nhiều mặt ranh giới thì ta có hàng loạt
BĐTK tơng ứng. Càng xuống sâu, tốc độ truyền sóng tăng dần và độ cong
của BĐTK càng giảm dần.
Loại BĐTK nh đã xét ở trên tơng ứng với một nguồn nổ và thu
sóng đồng thời ở nhiều điểm khác nhau và đợc gọi là BĐTK điểm nổ
chung. Khi mặt ranh giới nghiêng, biểu đồ thời khoảng của sóng phản xạ
không đối xứng qua điểm nổ, điểm cực tiểu của BĐTK dịch chuyển về
phía mặt ranh giới nâng lên, khoảng cách dịch chuyển này phụ thuộc vào
góc nghiêng và chiều sâu mặt ranh giới. Thời gian cực tiểu tmin và thời
gian ghi sóng tại điểm nổ t0 không trùng nhau, điều này gây khó khăn
cho quá trình xử lý số liệu. Để khắc phục nhợc điểm này, cần sử dụng

hệ thống điểm sâu chung, trong đó nguồn nổ và máy thu đợc sắp xếp
đối xứng nhau. Điều này cho phép thu đợc nhiều lần sóng phản xạ tại
một điểm trên mặt ranh giới và BĐTK luôn luôn đối xứng qua điểm giữa.
2.4.2. Biểu đồ thời khoảng của sóng phản xạ nhiều lần.
Giả sử trong môi trờng có mặt ranh giới R có góc nghiêng , tốc độ
truyền sóng trong môi trờng lớp phủ bằng v (hình 2.13).
Nếu gọi B là ảnh gơng của B qua R thì đờng đi OABCS từ nguồn
O đến S sẽ bằng quãng đờng OBS. Điểm B cũng nh các điểm phản xạ
khác đều nằm trên R(ảnh gơng của tuyến quan sát qua R). Nh vậy sóng
phản xạ 2 lần từ R có thể xem nh sóng phản xạ 1 lần từ R nằm ở chiều
sâu h và nghiêng so với phơng nằm ngang góc 2.
Phơng trình biểu đồ thời
t
khoảng của sóng phản xạ 2 lần có dạng:
x=

1
4h'2 + x 2 - 4h' x sin 2
2

h
h'
=
sin sin2

hay h' = h

sin 2
sin

Từ đó có phơng trình BĐTK
của sóng phản xạ 2 lần dới dạng:
1
sin 2 2
sin 2 2
2
t=
+
4h 2
x
4hx
v
sin 2
sin 2

P

O

B

S


2

R


A

C
B

v1
R

v2


R

Hình 2.13. Biểu đồ thời khoảng
của sóng phản xạ 2 lần


32


Thăm dò địa chấn trong địa chất dầu khí

Tơng tự nh trên, phơng trình BĐTK của sóng phản xạ m lần đợc
viết dới dạng:
t=

1
sin2 m
sin 2m
2
4h 2
+

x
4hx
v
sin 2
sin 2

Trong trờng hợp mặt phản xạ nằm ngang ( = 0), phơng trình
BĐTK sóng phản xạ m lần có dạng:
t=

1
v

4mh 2 + x 2

Biểu đồ thời khoảng sóng phản xạ nhiều lần có dạng hypecbol,
trùng với biểu đồ thời khoảng sóng phản xạ 1 lần phản xạ từ mặt ranh
giới có chiều sâu h và góc nghiêng m. Chiều sâu h đợc xác định theo
công thức:

h' =

sin m
h
sin

(m < 900)

Biểu đồ thời khoảng của sóng phản xạ nhiều lần và sóng phản xạ 1
lần cùng liên hệ với mặt ranh giới có các đặc điểm khác nhau:

- Thời gian t0 của sóng phản xạ m lần và sóng phản xạ 1 lần có mối
t m0 mt 10
quan hệ:
m
1
Khi = 0, ta có: t 0 = mt 0

- Thời gian cực tiểu của biểu đồ thời khoảng sóng phản xạ m lần và
sóng phản xạ 1 lần có mối quan hệ: t minm mt 1min .
Khi = 0, ta có: t minm = mt 1min = mt 10
2.4.3. Biểu đồ thời khoảng Điểm sâu chung
Trong hệ thống địa chấn điểm sâu chung, điểm nổ và điểm thu
luôn đối xứng nhau qua điểm giữa, điều này cho phép thu nhiều lần sóng
phản xạ tại một điểm trên mặt ranh giới và dạng biểu đồ thời khoảng luôn
luôn đối xứng qua điểm giữa kể cả trờng hợp mặt ranh giới nghiêng.
Ngoài ra còn cho phép kéo dài biểu đồ thời khoảng để tăng hiệu ứng định
hớng và khi thu nhiều lần sóng phản xạ từ cùng một điểm trên mặt ranh
giới sẽ tăng hiệu ứng thống kê.
Do tính chất đối xứng của biểu đồ thời khoảng nên t0 = tmin
Trên hình 2.14 thể hiện biểu đồ thời khoảng ĐSC trong trờng hợp
mặt ranh giới nghiêng, hi là chiều sâu pháp tuyến tại điểm nổ 0i, 0*i là
nguồn nổ ảo của 0i.
Ta có:
33


Mai Thanh Tân

0 *i .S i
=

t=
v

4 hi2 + x 2 + 4 hi x . sin , h i = h 0

Thay hi vào biểu thức trên ta có:
1
t=
4h02 + x 2 cos
v
Trong đó: t 0 =

2h0
. Ký hiệu
v

vĐSC =

2
hay t = t0 +

x
sin
2

x 2 cos 2
v2

v
và gọi là tốc độ điểm sâu

cos

chung, ta có:

x2
t= t + 2
vĐSC
2
0

Phân tích công thức này, có thể rút ra các nhận xét :
- Biểu đồ thời khoảng ĐSC có dạng hypecbon đối xứng và luôn có
cực tiểu nằm trên gốc toạ độ.
- Độ cong của biểu đồ thời khoảng ĐSC không chỉ phụ thuộc tốc độ
truyền sóng mà còn phụ thuộc góc nghiêng mặt ranh giới (vĐSC = v/ cos)
- Phơng đổ của mặt ranh giới không ảnh hởng tới đặc điểm biểu đồ
thời khoảng.
t
t(x)

a
o

o*i
hi

si

x

v

M



oi
b

c

z

Hình 2.14. Sơ đồ tia và biểu đồ thời khoảng ĐSC.
a. Sơ đồ tia hệ thống điểm nổ chung; b. Sơ đồ tia hệ thống ĐSC;
c. Biểu đồ thời khoảng ĐSC

2.4.4. Biểu đồ thời khoảng sóng phản xạ trong môi trờng phân lớp
Trong môi trờng trầm tích phân lớp có nhiều mặt ranh giới trung
gian nên sóng không truyền theo các tia thẳng mà theo các đoạn gẫy khúc,
34


Thăm dò địa chấn trong địa chất dầu khí

chính vì vậy biểu đồ thời khoảng của sóng phản xạ quan sát đợc có những
đặc điểm khác với môi trờng lớp phủ đồng nhất.
Chúng ta xét môi trờng 3 lớp đợc phân chia bởi các mặt ranh giới
R1 và R2, chiều dày và tốc độ của các lớp thứ nhất và thứ 2 là h1, h2 và v1, v2
(hình 2.15).

Biểu đồ thời khoảng của sóng phản xạ từ mặt ranh giới R2 có dạng:
t=

2h 1
2h 2
+
v1 cos v 2 1 2 sin 2

x = 2h1tg +

2nh 2
1 n 2 sin 2

ở đây là góc đổ của tia sóng trên R1; n = v2/v1.
Trong trờng hợp môi trờng gồm m lớp có chiều dày h1, h2....hm-1 và
tốc độ v1, v2,...vm-1 thì biểu đồ thời khoảng của sóng phản xạ từ lớp có tốc
độ truyền sóng vm-1 đợc viết nh sau:
m 1

hi
t = 2
;
i =1 v i cos i

m 1

x = 2 h i tg i
i =1

ở đây i là góc lệch của tia sóng thứ i.

Trên cơ sở định luật khúc xạ góc đợc xác định theo công thức:
sin 01 sin 2
sin m1
=
= .... =
v1
v2
vm 1
Từ các công thức trên cho thấy đặc điểm của biểu đồ thời khoảng sóng
phản xạ trong môi trờng nhiều lớp nh sau:
- Trong môi trờng phân lớp nằm ngang, biểu đồ thời khoảng của sóng
phản xạ là đờng đối xứng qua trục tung.
- ở gần điểm nổ biểu đồ thời khoảng của sóng phản xạ có dạng
hypecbol gần trùng với BĐTK sóng phản xạ có cùng t1 tính cho trờng hợp lớp
phủ đồng nhất.
- ở xa điểm nổ, biểu đồ thời khoảng có dạng gần nh đờng
thẳng. Tốc độ biểu kiến của sóng trong vùng này gần nh không đổi và
bằng tốc độ truyền sóng của lớp có tốc độ lớn nhất trong môi trờng lớp
phủ. Điều này cho thấy ở xa nguồn đờng đi của sóng nằm chủ yếu
trong lớp có tốc độ lớn nhất, biểu đồ thời khoảng của sóng phản xạ từ
mặt ranh giới thứ n có dạng tơng tự nh biểu đồ thời khoảng sóng đầu
liên hệ với ranh giới n-1.
- Trong môi trờng phân lớp, với các mặt phản xạ khác nhau sẽ quan sát
đợc các biểu đồ thời khoảng khác nhau. Các biểu đồ thời khoảng tơng ứng
35


Mai Thanh Tân

với mặt phản xạ nông có độ cong lớn hơn các biểu đồ thời khoảng liên hệ với

mặt phản xạ sâu.
t

o
h1

s




x
v1
R1
v2

h2

R2

Hình 2.15. Biểu đồ thời khoảng
sóng phản xạ trong môi trờng 3 lớp
2.5. Độ phân giải địa chấn.

Môi trờng địa chất đặc biệt là trong đá trầm tích có tính chất phân
lớp. Các lớp này có thể khác nhau về thành phần thạch học, tính cơ lý, độ
hạt, sự khác nhau này có thể theo chiều thẳng đứng hay theo chiều
ngang. Độ phân giải của phơng pháp địa chấn là khả năng phân biệt rõ hai
đối tợng địa chất nằm sát nhau cả phơng thẳng đứng và phơng nằm
ngang trên băng ghi địa chấn.

2.5.1. Độ phân giải thẳng đứng.
Độ phân giải thẳng đứng là khả năng phân biệt đợc hai mặt phản xạ
sát nhau trên băng ghi địa chấn. Nh vậy độ phân giải càng cao thì khả
năng phân biệt các mặt phản xạ càng sít nhau. Độ phân giải thẳng đứng phụ
thuộc vào tần số, tốc độ truyền sóng, tính chất của môi trờng và thờng
thay đổi trong phạm vi 1/4 bớc sóng :
v
vT
=
=
h =
.
4
4
4f
Trong đó: là bớc sóng, v là tốc độ, T là chu kỳ, f là tần số.

36


Thăm dò địa chấn trong địa chất dầu khí

Trong thăm dò dầu khí, giả sử nguồn phát sóng có tần số 40Hz, tốc
độ sóng dọc trong đá cát kết là 3000m/s thì độ dầy nhỏ nhất giữa hai tầng
phản xạ có thể phân biệt đợc trên băng ghi là:

h = 3000 / (4x40) = 18m
ở các lớp đất đá nằm ở nông, tốc độ khoảng 1500 ữ 2000m/s và tần
số khoảng 50Hz, khi đó bớc sóng = 30 ữ 40m và độ phân giải thẳng
đứng để phân biệt các mặt phản xạ là 5 ữ10m. ở chiều sâu lớn hơn, tốc độ

có thể tăng lên 5000 ữ 6000m/s, do hiệu ứng lọc của quả đất, tần số giảm
còn khoảng 20Hz. Trong trờng hợp đó bớc sóng tăng lên khoảng 250 ữ
300m và độ phân giải là 35 ữ 75m.
Một số thí dụ về mối quan hệ giữa độ phân giải thẳng đứng với tốc độ
và tần số đợc nêu trên bảng 2.1
Bảng 2.1

v(m/s)

f (Hz)

h (m)

2000
3000
4000
5000

50
40
30
20

10
18
33
62

Trong địa chấn phản xạ liên tục phân giải cao thờng dùng nguồn phát
có tần số cao (f = 2.5 ữ 7.5KHz đối với hệ Transducer; f = 400 ữ 4000Hz đối

với hệ Boomer). Giả sử dùng nguồn phát sóng có tần số là 400Hz, tốc độ
truyền sóng trong đá trầm tích là 1800m/s thì độ dầy nhỏ nhất có thể xen giữa
hai tầng phản xạ sẽ là: h = 1800 / (4x400) = 1.125 m
2.5.2. Độ phân giải ngang.
Độ phân giải ngang là khả năng phân biệt các đối tợng khác nhau
theo chiều ngang trên lát cắt địa chấn. Độ phân giải này phụ thuộc vào diện
tích đới Fresnel thứ nhất. Năng lợng sóng đến một điểm trên mặt quan sát
từ một mặt phản xạ không phải là một điểm mà thực chất đến từ một diện
tích nhất định trên mặt phản xạ. Diện tích đó gọi là đới Fresnel thứ nhất, đới
này đợc giới hạn bới khoảng cách giữa hai mặt sóng cách nhau 1/4 bớc
sóng. Năng lợng của đới này đóng góp chủ yếu vào tín hiệu phản xạ so với
các đới khác (hình 2.16).
Sóng địa chấn truyền đi trong môi trờng với mặt sóng là hình cầu,
khi truyền sóng mặt sóng mở rộng dần và biên độ giảm. Trong môi trờng
có tốc độ không đổi thì biên độ tỷ lệ nghịch với khoảng cách đến nguồn r.
Trong thực tế, tốc độ tăng theo chiều sâu nên biên độ giảm nhanh
hơn. Sự mở rộng mặt sóng theo chiều sâu cũng dẫn đến việc giảm dần độ
37


Mai Thanh Tân

phân giải. Khi mặt sóng cầu đạt đến mặt ranh giới phản xạ có chiều sâu h,
thì diện tích hình tròn nằm trên mặt phản xạ đợc giới hạn bởi mặt sóng có
bán kính r =

z
2

vz

2 f

=

đợc gọi là đới Fresnel đầu tiên.
Nguồn phát

r

Mặt phản xạ

Đới Fresnel

Hình 2.16. Đới Fresnel
Bán kính của đới này phụ thuộc vào khoảng cách đến nguồn và bớc
sóng . Do =

v
nên bán kính đới Fresnel đầu tiên này phụ thuộc vào tần
f

số. Với tần số cao thì đới này nhỏ và ngợc lại.
Một số thí dụ về mối quan hệ giữa độ phân giải ngang với tốc độ và
tần số đợc nêu trên bảng 2.2. Giả sử với chiều sâu khoảng 3000m, tần số
40Hz và tốc độ 3000m/s thì bán kính đới Fresnel là r = 335m.
Bảng 2.2
t(s)
1
2
3

4

v(m/s)
2000
3000
4000
5000

f (Hz)
50
40
30
20

r(m)
141
335
362
1180

Trong phơng pháp địa chấn phản xạ phân giải cao, để đạt độ phân giải
mong muốn ngời ta sử dụng dải tần số phát từ 1 ữ 10 KHz và bớc sóng địa

38