Calculus and its applications 10th edition bittinger test bank

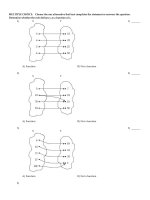
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Decide whether the limit exists. If it exists, find its value.
1)
1) _______
Find

f(x) and

A) -5; -2

f(x).

B) -7; -5

C) -7; -2

D) -2; -7

2)

2) _______
Find

f(x) and

A) 3; -1

f(x).

B) 3; 1

C) - 3; -1

D) -1; 3

3)

3) _______
Find

f(x).

A) Does not exist

B) 2

C) 1

D) 0

4)

4) _______
Find

f(x).

A) Does not exist

B) 1

C) -1

D) 0


5)

5) _______
Find

f(x).

A) -1

B) 0

C) -2

D) Does not exist

6)

6) _______
Find

f(x).

B) -2

A) 2

C) Does not exist

D) 0

7)

7) _______
Find

f(x).

A)

B) Does not exist

C) 0

D) 1

8)

8) _______
Find

f(x).

B) -1

A) 0

9)
Find

f(x).

C) 1

D) Does not exist


9)

_______
A) Does not exist

B) 0

C) -2

D) -1

10)

10) ______
Find

A) -1

f(x).

B) Does not exist

C) 0

Use the graph to determine whether each statement is true or false.
11)

A) True

11) ______

B) False

12)

12) ______

A) False
13)

D) -2

B) True


13)

___
___

A) False

B) True

14)

14) ______
f(x) = 2

A) True

B) False

15)

15) ______

A) True
16)

B) False
16)


______
A) True

B) False

17)

17) ______

A) True

B) False

18)

18) ______

A) True

B) False

19)

19) ______

A) True
20)

B) False


20)

___
___

A) False

B) True

Graph the function and then find the specified limit. When necessary, state that the limit does not exist.
21)
f(x) =
;
f(x)

A)

B)
f(x) = 3

C)

f(x) = 0

D)
f(x) = 7

21) ______


f(x) = 2

22)

22) ______

f(x) =

;

A)

f(x)

B)
f(x) = 0

C)

f(x) = 5

D)
f(x) = 5

f(x) = -5


23)

23) ______
f(x) =

;

f(x)

A)

B)
f(x) = 0

C)

D)
f(x) = 0

24)
f(x) = -4

f(x) does not exist

;

f(x)

f(x) does not exist


24)

___
___

A)

B)

f(x) = -4

C)

f(x) = 4

D)
f(x) = 0

25)

f(x) = 0

25) ______
y = x2 - 5;

f(x)


A)

B)
f(x) = -5

f(x) = 5

C)

D)
f(x) = -5

f(x) = 5

26)

26) ______
f(x) =

;

A)
f(x) = 5

f(x)


B)
f(x
)=
5

C)

D)
f(x) = 1

f(x) = -3

27)

27) ______
y(x) =

;

A)
f(x) does not exist

f(x)


B)
f(x
)=
9

C)

D)
f(x) = -4

f(x) does not exist

28)

28) ______
f(x) =

;

A)
f(x) = 4

f(x)


B)
f(x
)=
3

C)

D)
f(x) does not exist

29)

f(x) = 3

29) ______
y=

- 2;

f(x)

A)
f(x) = -2

B)
f(x
)=
2

C)

D)
f(x) = 0

f(x) = 0

Solve the problem.
30) Given is a graph of a portion of the postage function, which depicts the cost (in cents) of mailing
a letter, p, versus the weight (in ounces) of the letter, x. Find each limit, if it exists:

p(x),

p(x),

p(x)

30) ______


A) 77; 99; 77
C) 99; 77; does not exist

B) 77; 99; does not exist

D) 77; 77; 77

31) Given is a graph of a portion of the postage function, which depicts the cost (in cents) of mailing
a letter, p, versus the weight (in ounces) of the letter, x. What is the postage for a letter weighing

31) ______

Is the postage function continuous?

A) 55 cents; 55 cents; 77 cents; no
C) 55 cents; 77 cents; 77 cents; no

B) 33 cents; 55 cents; 77 cents; no
D) 55 cents; 55 cents; 77 cents; yes

32) Suppose that the cost, p, of shipping a 3-pound parcel depends on the distance shipped, x,
according to the function p(x) depicted in the graph. Is p continuous at

at

32) ______
at

at

A) No; no; yes; no
C) Yes; no; no; no

B) Yes; yes; yes; no
D) Yes; no; yes; no

33) Suppose that the cost, p, of shipping a 3-pound parcel depends on the distance shipped, x,
according to the function p(x) depicted in the graph. Find each limit, if it exists:

p(x),

p(x),

p(x)

33)


______
A) 5; 10; 15
C) 5; does not exist; does not exist

B) 5; does not exist; 15
D) 5; 5; 15

34) Suppose that the cost, C, of producing x units of a product can be illustrated by the given graph.
Find each limit, if it exists:

p(x),

p(x),

p(x)

A) 200; 300; does not exist

C) 200; 300; 200

B) 200; 200; 200
D) 200; does not exist; does not exist

35) Suppose that the cost, C, of producing x units of a product can be illustrated by the given graph.
Is

34) ______

35) ______

continuous at

A) Yes; yes; yes

B) No; no; no

C) Yes; no; no

D) Yes; no; yes

36) Suppose that the unit price, p, for x units of a product can be illustrated by the given graph. Find
each limit, if it exists:

p(x),

p(x),

p(x),

p(x)

36)


______
A) 8; 8; does not exist; 8
C) 10; 8; does not exist; 8

B) 8; 8; 8; 8
D) 10; 8; 8; 8

37) Suppose that the unit price, p, for x units of a product can be illustrated by the given graph. Is p

37) ______

continuous at

A) No; no; no

B) No; yes; no

C) Yes; no; yes

D) No; yes; yes

38) Consider the learning curve defined in the graph. Depicted is the accuracy, p, expressed as a
percentage, in performing a series of short tasks versus the accumulated amount of time spent
practicing the tasks, t. Is

A) Yes; yes; yes

continuous at

B) Yes; no; yes

at

at

C) Yes; no; no

D) No; no; no

39) Consider the learning curve defined in the graph. Depicted is the accuracy, p, expressed as a
percentage, in performing a series of short tasks versus the accumulated amount of time spent
practicing the tasks, t. Find each limit, if it exists:

p(x),

p(x),

p(x)

38) ______

39)

______
A) 40; 100; 100
C) 100; 100; 100

B) 40; 100; does not exist
D) 40; 40; 40

Find the limit, if it exists.
40)
(8x + 8)
A) -40

40) ______
B) 16

C) 8

D) 56

41)

41) ______
(
A) 0

+ 8x - 2)

(
A) 0

- 5)

B) Does not exist

C) -18

D) 18

42)

42) ______
B) Does not exist

C) -5

D) 5

43)

43) ______
( +5
- 7x + 1)
A) Does not exist

B) 0

C) 15

D) 29

44)

44) ______
(2
A) 63

-2

+4

+

- 5)
B) -1

C) 127

D) 31

45)

45) ______
A) Does not exist

B) 2

C) 4

D) 0

46)

46) ______
A) 14

B) 0

C) 1

D) Does not exist

In the exercise below, the initial substitution of x = a yields the form 0/0. Look for ways to simplify the function
algebraically, or use a table and/or graph to determine the limit. When necessary, state that the limit does not exist.
47)
47) ______
A) Does not exist

B) 1

C) 7

D) 14

48)

48) ______
A) -16

B) -8

C) 1

D) Does not exist

49)

49) ______
A) - 3

B) Does not exist

50)

C) 4

D) 0
50) ______

A)

-


B)

C)

D)

-

51)

51) ______
A) -3

B)

C)

D) 3
-

52)

52) ______
A) - 6

B) -12

C) 12

D) 6

53)

53) ______
A) -8

B) 8

C) -4

D) 16

54)

54) ______
A) 0

Find the limit, if it exists.
55)
-2
A) 2

B)

C) 7

D)

55) ______
B) 0

C) -2

D) Does not exist

56)

56) ______
A) ±14

B) Does not exist

C) 196

D) 14

57)

57) ______
A) -1

B) Does not exist

C) 1

D) 0

58)

58) ______
A) Does not exist

B) ±

C) 93.5

D)

59)

59) ______
A) 0

B) Does not exist

C) 3.5

Determine whether the function shown is continuous over the interval (-5, 5).
60)

D) 7


60)

A) Yes

___
___

B) No

61)

61) ______

A) Yes

B) No

62)

62) ______

A) Yes
63)

B) No


63)

A) Yes

___
___

B) No

64)

64) ______

A) Yes

B) No

65)

65) ______

A) Yes
66)

B) No


66)

A) Yes

___
___

B) No

67)

67) ______

A) Yes

B) No

68)

68) ______

A) Yes
Use the graph to answer the question.
69) Is f continuous at x = 1?

B) No


69)

A) Yes

___
___

B) No

70) Is f continuous at x = 1?

A) No

70) ______

B) Yes

71) Is f continuous at x = -1?

A) Yes
72) Is f continuous at x = 3?

71) ______

B) No


72)

A) Yes

___
___

B) No

73) Is f continuous at x = 0?

A) Yes

73) ______

B) No

74) Is f continuous at x = 4?

A) No
75) Is f continuous at x = 0?

74) ______

B) Yes

75)

___
___

A) Yes

B) No

76) Is f continuous at x = -1?

76) ______

A) Yes

B) No

77) Is f continuous at x = 2?

77) ______

A) Yes

B) No

Evaluate or determine that the limit does not exist for each of the limits

and

for the given function f and number d.
78)

78) ______
f(x) =

; d = -1