Hệ thức lượng và tỉ số lượng giác trong tam giác vuông- Võ Trường Hải- FULL- Bản đẹp – Xuctu.com

<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1>

<b>1. HỆ THỨC LƯỢNG TRONG TAM GIÁC </b>

<b>A. KIẾN THỨC: </b>

<b>I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG: </b>

<b>1. Một số hệ thức: </b>

1) c2_{= ac}’_{, b}2_{= ab}’

2) h2_{= b},_c,

3) ah = bc

4) 2 = 2 + 2

1 1 1

h b c

5) a2_{= b}2_{+ c}2

-Với tam giác đều cạnh là a, ta có:

2

a 3 a 3

h ; S

2 4

= =

<b>2. Ví dụ: </b>

VD1. Cho tam giác ABC có AB>AC, kẻ trung tuyến AM và đường cao AH.

Chứng minh:

2

2 2 2

2 2

BC
a) AB AC 2AM

2
b) AB AC 2BC.MH

+ = +

− =

VD2.Cho hình thang ABCD (AB//CD có AB = 3cm; CD = 14cm; AC = 15cm; BD =

8cm.

a) Chứng minh AC vng góc với BD.

b) Tính diện tích hình thang.

VD3.Tính diện tích hình bình hành ABCD biết AD = 12; DC = 15; ∠ADC=700_.

<b>3. Bài tập cơ bản: </b>

A

C
H

B

c b

</div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>

1.Cho tam giác ABC vuông cân tại A, trung tuyến BD. Gọi I là hình chiếu của C

trên BD, H là hình chiếu của I trên AC.

Chứng minh: AH = 3HI.

2. Qua đỉnh A của hình vng ABCD cạnh bằng a, vẽ một đường thẳng cắt BC ở

E và cắt đường thẳng DC ở F.

Chứng minh: 1 ₂ 1₂ 1₂
AE +AF =a

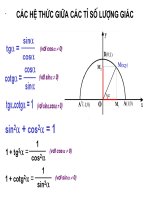
<b>II. TỈ SỐ LƯỢNG GIÁC CỦA GĨC NHỌN: </b>

<b>1. Định nghĩa: </b>

<b>2. Tính chất: </b>

- Một số hệ thức lượng giác cơ bản:

2 2 sin cos

sin cos 1; tg .cot g 1; tg ; cot g

cos sin

α α

α + α = α α = α = α =

α α

- Chú ý:

+) 0<sinα <1; 0<cos <1;α

+) Khi góc α tăng từ 0o_{đến 90}o_{thì sin}α_{và tg}α_{tăng cịn cos}α_{và cotg}α_giảm.

+) Nếu hai góc phụ nhau thì sin của góc này bằng cos của góc kia, tg của góc này

bằng cotg của góc kia và ngược lại.

sinα =cos ;β cosα =sin ;β tgα =cotg ;β cot gα = βtg

+) Tỉ số lượng giác của 3 góc đặc biệt.

<b>3. Bài tập: </b>

<b>Bài 1: Cho tam giác ABC vuông tại A, AB = 4cm; BC = 6 cm. Tính các TSLG của </b>

</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>

Nhận xét: Tam giác vuông khi biết độ dài 2 cạnh ta thường dùng định lí

Py-ta-go tính cạnh cịn lại. Sau đó dùng định nghĩa TSLG để tính các TSLG của góc

nhọn.

<b>Bài 2: Chứng minh rằng sin</b>α < tgα; và cosα< cotgα<b>. </b>

HD: Xét tam giác ABC vuông tại A, B = α.

sinB = AC

BC<b> ; tgB = </b>
AC
AB

Vì BC > AC nên AC

BC<
AC

AB Suy ra sinα < tgα;

Chứng minh tương tụ ta được cosα< cotgα.

<b>Bài 3: Không dùng MTBT hoặc bảng số, hãy sắp xếp cã TSLG sau theo thứ tự </b>

tăng dần.

Cotg40o_{, sin50}o_{, tan70}o_{, cos55}o_.

HD: Theo định lí về TSLG của hai góc phụ nhau, ta có:

cos55o_{= sin35}o_{; Cotg40}o_{= tg50}o_.

Vì sin35o_{< sin50}o_{< tg50}o_{< tg70}o_.

Nên cos55o_{< sin50}o_{< Cotg40}o_{< tg70}o

<b>NX: Nhờ có tính chất sin</b>α < tgα mà ta có thể so sánh được các TSLG.

<b>Bài 4: Khơng dùng MTBT hoặc bảng số, tính nhanh gí trị các biểu thức sau: </b>

a) M = sin2₁₀o_{+ sin}2₂₀o_{+ sin}2₄₅o_{+ sin}2₇₀o_{+ sin}2₈₀o<b>_.</b>

b) N = tg35o_{. tg40}o_.tg45o_.tg50o_{. tg55}o_.

<b>Bài 5: </b>

a) Biết sinα= 5

13, hãy tính cosα, tgα, cotgα.

b) Biết tgα = 12

</div>
<span class='text_page_counter'>(4)</span><div class='page_container' data-page=4>

<b>Bài 6: Cho biểu thức: </b> 2 2

1 2 sin cos
A

sin cos

− α α

=

α − α với αkhác 45o<b>. </b>

a) Chứng minh rằng A sin cos
sin cos

α − α
=

α + α

b) Tính giá trị của A biết tg 1
3

α = .

HD:

a)

2 2

sin 2 sin cos cos
A

(sin cos )(sin cos )

α − α α + α
=

α − α α + α

b) A sin cos
sin cos

α − α
=

α + α chia cả tử và mẫu cho cosα.

NX. Nếu chi tg thì chia cả tử và mẫu cho sin.

Bài 7. Tìm x biết tgx + cotgx = 2.

HD.

Tìm 1 tỉ số lượng giác của góc đó.

sinx = cosx . Suy ra tgx = 1 = tg45o_.

Vậy x = 45o_.

<b>4. Bài tập tự luyện: </b>

<b>Bài 1: Cho tam giác ABC vuông tại A, AB = 20; AC = 21. Tính các TSLG của góc </b>

B và góc C.

<b>Bài 2: </b>

a) Biết cosα=3

4, hãy tính sinα, tgα, cotgα.

b) Biết cotgα = 8

15, hãy tính sinα, cosα, tgα.

<b>Bài 3: Không dùng MTBT hoặc bảng số, tính nhanh gí trị các biểu thức sau: </b>

a) M = sin2₄₂o_{+ sin}2₄₃o_{+ sin}2₄₄o_{+ sin}2₄₅o_{+ sin}2₄₆o_{+ sin}2₄₇o_{+ sin}2₄₈o<b>_.</b>

</div>
<span class='text_page_counter'>(5)</span><div class='page_container' data-page=5>

<b>Bài 4. Sắp xếp các TSLG sau theo thứ tự tăng dần: </b>

Sin49o_{, cotg15}o_{, tg65}o_{, cos50}o_{, cotg41}o_.

<b>Bài 5. Chứng minh rằng giá trị của các biểu thức sau không phụ thuộc vào giá </b>

trị của góc nhọn α.

a) (cosα - sinα)2_{+ (cos}α_{+ sin}α₎2_.

b)

2 2

(cos sin ) (cos sin )
cos .sin

α − α − α + α
α α

<b>Bài 6: Cho tam giác nhọn ABC. Gọi a, b, c là lượt là độ dài các cạnh BC, CA, và </b>

AB.

a) Chứng minh răng: a b c

sin A =sin B =sin C

b) Có thể xảy ra đẳng thức sinA = sinB – sinC không ?

<b>III. HỆ THỨC VỀ CẠNH VÀ GĨC TRONG TAM GIÁC VNG: </b>

1. Trong tam giác vng mỗi cạnh góc vng bằng:

a) Cạnh huyền nhân với sin góc đối hoặc nhân với cos của góc kề.

b) Cạnh góc vng kia nhân với tg góc đối hoặc nhân với cotg góc kề.

b a sin B acosC ctgB ccot gC
c acosB asinC bctgB btgC

= = = =

= = = =

<b>2. Bài tập: </b>

Bài 1: Cho hình thang ABCD có

o o

A= =D 90 , C=50 . Biết AB = 2; CD = 1,2. Tính

diện tích hình thang.

HD. Vẽ BH⊥CD thì BH = AD = 1,2; DH = AB

= 2.

Xét tam giác HBC vng tại H, ta có:

50°
1,2

2

H

D C

</div>
<span class='text_page_counter'>(6)</span><div class='page_container' data-page=6>

HC = HB.cotgC ≈ 1

CD =CH + HD ≈ 3.

Diện tích hình thang ABCD là:

(AB CD).AD

S 3

2

+

= = (đvdt)

Nhận xét: Vẽ BH⊥CD.

<b>Bài 2: Tam giác ABC có AB = 4; AC = 3,5. Tính diện tích tam giác ABC trong hai </b>

trường hợp:

a) o

A=40

b) o

A=140

HD. Tính đường cao CH. Tính diện tích tam giác.

Nhận xét: Một cách tổng quát ta chứng minh được rằng: Diện tích tam giác bằng

nửa tích hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai

cạnh ấy.

1 1 1

S a.b.sin C b.c.sin A c.a.sin B

2 2 2

= = =

<b>Bài 3: Cho tam giác ABC với đường phân giác trong của góc BAC là AD. Biết </b>

AB = 6, AC = 9 và o

A=68 , tính độ dài AD.

<b>Hướng dẫn giải </b>

Gọi diện tích các tam giác ABD, ADC và ABC là lượt là S1, S2, S. Ta có:

1 1

2 2

1

S AB.AD.sin A
2

1

S AD.AC.sin A
2

=

=

1

S AB.AC.sin A
2

=

9
6

2
1

D

C
B

</div>
<span class='text_page_counter'>(7)</span><div class='page_container' data-page=7>

Vì: S = S1 + S2 .

Nên : 1 2

1 1 1

AB.AD.sin A AD.AC.sin A AB.AC.sin A

2 +2 = 2

1 2

AB.AD.sin A AD.AC.sin A AB.AC.sin A

⇔ + =

o

o o

1 2

AB.AC.sin A 6.9.sin 68

AD 6

AB.sin A AC.sin A 6.sin 34 9 sin 34

⇔ = = ≈

+ +

<b>Bài 4. Tam giác ABC vuông tại A, đường cao AH, biết HB = 9; HC = 16. Tính góc </b>

B và góc C.

KQ: o

B≈53 7

<b>Bài 5: Giải tam giác ABC vuông tại A biết: </b>

a) a = 18; b = 8.

b) b = 20; o

C=38 .

<b>Bài 6: Tam giác ABC cân tại A, </b> o

B=65 , đường cao CH = 3,6. Hãy giải tam giác

ABC.

<b>4. Bài tập tự luyện: </b>

<b>Bài 1: Tam giác ABC vuông tại A, AB = 17cm; </b> o

C=62 . Tính độ dài đường trung

tuyến AM.

<b>Bài 2: Cho hình thang cân ABCD (AB//CD), AB = 2, CD = 5 và </b> o

A=127 _{. Tính diện}

tích hình thang.

<b>Bài 3: Hình bình hành ABCD có AD = 4,3; CD = 7,5 và </b> o

D=64 . Tính diện tích

hình bình hành.

<b>Bài 4: Độ dài hai đường chéo của một tứ giác là 9 và 13. Góc nhọn giữa hai </b>

đường chéo là 48o_{. Tính diện tích tứ giác.}

Bài 5: Giải tam giác ABC vuông tại A biết:

a) a = 12; o

</div>
<span class='text_page_counter'>(8)</span><div class='page_container' data-page=8>

b) b = 13; c = 20.

<b>Bài 6: Giải tam giác ABC biết: AB = 6,8; </b> o

A=70 ; B=50o

Bài 7: Giải tam giác ABC biết: AB= 4,7; BC = 7,2; o

A=66

</div>
<span class='text_page_counter'>(9)</span><div class='page_container' data-page=9>

<b>Bộ phận bán hàng: 0918.972.605</b>

<b>Đặt mua tại: />

<b>FB: facebook.com/xuctu.book/</b>

<b>Email: </b>

<b>C. BÀI TẬP BỔ SUNG: </b>

<b>Bài 1 </b>

Cho tam giác ABC, đường thẳng d// BC cắt AB tại M, cắt AC tại N. Gọi I,

J lần lượt là trung điểm của MN và BC.

a/ Chứng minh rằng: A, I, J thẳng hàng.

b/ Gọi P, Q, H lần lượt là hình chiếu của M, N, A lên BC, O = MP ∩ NQ,

R là trung điểm của AH. Chứng minh rằng: J, O, R thẳng hàng.

<b>Hướng dẫn giải </b>

<b>a/ áp dụng định lý Talét cho tam giác ABC ta có: </b>

MN =AN ⇔ MN / 2=AN ⇔ IN =AN

BC AC BC / 2 AC JC AC

Nên: A, I, J thẳng hàng.

b/ Gọi S là trung điểm của PQ ⇒ I, O, S thẳng hàng

và O là trung điểm của IS, AH // IS ⇒ theo câu a thì ta có J, O, R thẳng hàng.

<b>Bài 2 </b>

Cho tam giác ABC vuông tại A, phân giác trong AD, phân giác ngoài

B J C

N
I

M

P H Q

O
R

</div>
<span class='text_page_counter'>(10)</span><div class='page_container' data-page=10>

AE. Cho biết AB < AC. Chứng minh các hệ thức sau:

a/ 1 + 1 = 2

AB AC AD b/ − =

1 1 2

AB AC AE

<b>Hướng dẫn giải </b>

<i><b> </b></i>

Vẽ DH ⊥ AB, DK ⊥ AC ⇒ DH = DK = AD

2

<b>a/ Áp dụng định lý Talét cho ∆ABC ta có: </b>

= = ⇔ = ⇔ =

DK CD 1 AD 1 1 1

AB CB 2 2AB 2 AB 2AD

= = ⇔ = ⇔ =

HD CD 1 AD 1 1 1

AC CB 2 2AC 2 AC 2AD ⇒ + = =

1 1 2 2

AB AC 2AD AD.

Cách khác:

<i><b>Chú ý:</b> SABC = </i>

2
1

<i>AB.ADsin</i>∠<i>(AB;AC) </i>

a/ Ta có: SABC = 1

2 AB.AC = SABD + SACD =
1

2 AB.ADsin45

0₊1

2 AC.ADsin45

0

⇒AB.AC = 2 (AB+AC)AD
2

⇒ ₌ _⇔ + ₌

+

AB.AC 2AD AB AC 2

AB AC 2 AB.AC AD

⇔ 1 + 1 = 2

AB AC AD

b/ Ta có: SABC = 1

2 AB.AC = SAEC - SABE =
1

2 AE.ACsin135

0_-1

2AB.AEsin45

0

⇒ AB.AC = AE

2 (AC - AB)

⇒ =

−

AB.AC AE

AC AB 2

B
A

C
E

</div>
<span class='text_page_counter'>(11)</span><div class='page_container' data-page=11>

−

⇔AC AB= 2

AB.AC AE

⇔ 1 − 1 = 2

AB AC AE.

<b>Bài 3: </b>Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến AM.

Chứng minh các hệ thức sau:

a/ =   −

 

2

MH BM

2 1

BH AB b/ + = +

2

2 2 2 BC

AB AC 2AM

2

<b>Hướng dẫn giải </b>

a/ Do tam giác ABC vuông tại A nên ta có:

=AB2 = AB2

BH

BC 2BM

−
= − = − AB2 =2BM2 AB2

MH MB BH BM

2BM 2BM

⇒ = − = − =   −

 

2

2 2 2 2

2 2

MH 2BM AB 2BM 2BM AB BM

. 2 1

BH 2BM AB AB AB .

b/ Ta có:

2 2 2

2 2 2

<i>AB</i> <i>AH</i> <i>HB</i>

<i>AC</i> <i>AH</i> <i>HC</i>

 ₌ ₊

= +





Suy ra: AB2_{+ AC}2_{= 2AH}2_{+ HB}2_{+ HC}2

= 2AH2_{+ (BM - HM)}2_{+ (MC + HM)}2

= 2AH2_{+ BM}2_{+ MC}2_+2HM2_{- 2BM.HM + 2MC.HM}

= 2(AH2_{+ HM}2_{) + (BC/2)}2_{+ (BC/2)}2_{= 2AM}2_{+ BC}2_/2.

<b>Bài 4: </b>Cho tam giác đều ABC, O là trung điểm của BC, một góc xOy =

600_{có cạnh Ox, Oy ln cắt AB, AC tại M và N.}

a/ Chứng minh rằng OB2_{= BM.CN}

b/ Chứng minh rằng tia MO, NO luôn là phân giác của góc BMN và

B
A

C
M

</div>
<span class='text_page_counter'>(12)</span><div class='page_container' data-page=12>

CMN

c/ Chứng minh rằng đường thẳng MN luôn tiếp xúc với một đường trịn

cố định khi góc xOy quay quanh O nhưng hai cạnh Ox, Oy vẫn cắt hai

cạnh AB và AC của tam giác ABC.

<b>Hướng dẫn giải </b>
a/ Ta có: ∠B = ∠C = 600

∠O1 + ∠O2 = 1200; ∠O1 + ∠M1 = 1200

⇒ ∠M1= ∠O2 ⇒ ∠N1 = ∠O1

⇒ ∆BOM ∆CNO
⇒BO/CN = BM/CO

⇔ BO.CO = BM.CN
⇔ BO2 _{= BM.CN}

b/ Từ (a) ta có: OM= BM⇔ OM =ON ⇔ OM= ON

NO CO BM CO BM OB

Mặt khác: ∠MBO = ∠MON = 600

⇔ ∆BOM ∆ONM
⇔ ∠M1 = ∠M2

⇒ OM là tia phân giác của ∠BMN .

c/ Do O là giao điểm của hai tia phân giác của ∠BMN và ∠MNC
⇒ O cách đều AB, MN và AC.

Gọi H là hình chiếu của O lên AB

Nên: OH = OB.sinB = a. 3 = a 3

2 2 4

Suy ra: MN luôn tiếp xúc với đường trịn cố định có tâm O bán kính a 3

4 .

A

B C

N
M

</div>
<span class='text_page_counter'>(13)</span><div class='page_container' data-page=13>

<b>Bài 5: </b>Cho tam giác đều ABC, trên các cạnh BC, AB, AC lấy ba điểm bất

kỳ O, M, N sao cho O khác B, C và ∠MON = 600_.

Chứng minh rằng: BM.CN ≤ BC2_{/4. Dấu bằng xảy ra khi nào?}

<b>Hướng dẫn giải </b>
Ta có: ∠BOM =1800 - ∠B - ∠BMO = 1200 - ∠BMO

Mà: ∠BOM = 1800 - ∠MON - ∠CON = 1200 - ∠CON

⇒ ∠BMO = ∠ CON
⇒ ∆BOM ∆CNO

⇒ BM/CO = BO/CN

⇔ BM.CN = BO.CO ≤  +  =

 

2 ₂

BO CO BC

2 4

<b>Bài 6: </b>Cho tam giác ABC có ba góc nhọn. Gọi H là trực tâm của tam giác

ABC, K là chân đường cao vẽ từ A của ∆ABC. Chứng minh rằng:

≤BC2

KH.KA

4 .

<i><b>Giải </b></i>

Xét ∆AKB và ∆CKH có: ∠AKB = ∠CKH = 900

∠BAK = ∠HCK (hai góc nhọn cạnh tương ứng vng góc)
⇒ ∆AKB ∆CKH

⇒ KA = KC

KB KH

⇒ = ≤ +  =

 

2 ₂

KB KC BC

KA.KH KB.KC

2 4

⇒ KH.KA≤BC2

4

<b>Bài 7: </b> Cho tam giác ABC vuông tại A. Chứng minh rằng:

A

B C

K
H

A

B C

M

O

</div>
<span class='text_page_counter'>(14)</span><div class='page_container' data-page=14>

∠ ₌
+

ABC AC

tg

2 AB BC

<b>Hướng dẫn giải </b>

a/ Xét ∆ABD có ∠A = 900_⇒_{tg ABD}∠ =AD ⇔_tg∠ABC =AD

AB 2 AB

Vẽ đường phân giác BD ta có:

+

= ⇔ = = =

+ +

DA BA DA DC DA DC AC

DC BC BA BC AB BC AB BC

⇒ ∠ =

+

ABC AC

tg

2 AB BC .

<b>Bài 8: </b>Cho hình thoi ABCD. Gọi R1, R2 lần lượt là bán kính các đường

trịn ngoại tiếp ∆ABD và ∆ABC. Gọi a là độ dài cạnh hình thoi.

a/ Chứng minh rằng: ₂ + ₂ = ₂

1 2

1 1 4

R R a .

b/ Tính diện tích hình thoi theo R1 và R2.

<b>Hướng dẫn giải </b>

a/ Giả sử trung trực cạnh AB cắt AC tại O1 và cắt BD tại O2

⇒ O1 và O2 là tâm các đường tròn ngoại tiếp ∆ABD và ∆ABC

⇒ O1A = R1 và O2B = R2.

∆O1AK ∆ABO ⇒ O A1 =AK ⇒R1 = a

AB AO a 2AO

(1)

∆O2BK ∆ABO ⇒ O A2 =BK ⇒R2 = a

AB BO a 2BO

(2)

Từ (1)_và(2)_⇒ = =

4 4

2 2

2 2

1 2

a a

4AO , 4BO

R R

⇒

(

+

)

=  + ⇔ =  + ⇔ + =

   

2 2 4 2 4

2 2 2 2 2 2 2

1 2 1 2 1 2

1 1 1 1 1 1 4
4 AO BO a 4a a

R R R R R R a .

b/ Ta có: SABCD = 2OA.OB

</div>
<span class='text_page_counter'>(15)</span><div class='page_container' data-page=15>

∆AOB ∆AKO2 ⇒ = ⇒ =
2

2 2

OA AB AB

OA

AK AO 2R

∆AOB ∼ ∆O1KB ⇒ = ⇒ =
2

1 1

OB AB AB

OB

KB O B 2R ⇒ =

4

1 2

AB
OA.OB

4R R

Xét ∆AOB ta có: AB2_{= OA}2_{+ OB}2 ⇔ = + = _ + _

 

4 4

2 4

2 2 2 2

2 1 1 2

AB AB 1 1

AB AB

4R 4R 4R 4R

+

⇒ ₌ _⇔ ₌

+

2 2 2 2

2 1 2 2 1 2

2 2 2 2

1 2 1 2

(R R ) 4R R
1 AB AB

4R R R R .

Vậy: = ⇒ ₌

+ +

4 4 3 3

1 2 1 2

ABCD

2 2 2 2 2 2

1 2 1 2 1 2

16R R 8R R

1

OA.OB . S

4R R (R R ) (R R ) .

<b>Bài 9: </b>Chứng minh rằng trong một tam giác bất kỳ ta có:

+ − _< _< +

a

b c a b c

m

2 2

<b>Hướng dẫn giải </b>
Xét ∆ABC có: AM > AB - BM

Xét ∆ACM có: AM > AC - MC

Cộng từng vế ta có: 2AM > AB + AC - BC ⇔ a > + −
b c a
m

2 .

Trên tia đối của tia MA lấy điểm D sao cho MA = MD ⇒ AB = CD

Xét ∆ACD có: AD < AC + CD = AC + AB ⇒ 2AM < AC + AB ⇒ a < +
b c
m

2 .

<b>Bài 10 </b>

CMR trong tứ giác lồi ABCD ta có bất đẳng thức: AB + CD < AC + BD

<b>Hướng dẫn giải </b>

Gọi O là giao điểm của hai đường chéo

Ta có:

AC + BD = (AO + OC) + (BO + OD) =

= (OA + OB) + (OC + OD)

</div>
<span class='text_page_counter'>(16)</span><div class='page_container' data-page=16>

⇒ AC + BD > AB + CD.

<b>BTVN </b>

<b>Bài 1: </b>Cho tam giác ABC, kẻ đường cao AH, gọi C1 là điểm đối xứng của H qua

AB, B1 là điểm đối xứng của H qua AC. Gọi giao điểm của B1C1 với AC và AB là

I và K. Chứng minh rằng đường BI, CK là đường cao của tam giác ABC.

<b>Bài 2: </b>Cho tam giác ABC cân tại A và H là trung điểm của cạnh BC. Gọi I là

hình chiếu vng góc của H lên cạnh AC và O là trung điểm của HI. Chứng

minh rằng hai tam giác BIC và AOH đồng dạng với nhau và AO vng góc với

BI.

</div>
<span class='text_page_counter'>(17)</span><div class='page_container' data-page=17>

<b>Bộ phận bán hàng: 0918.972.605</b>

<b>Đặt mua tại: />

<b>FB: facebook.com/xuctu.book/</b>

</div>

<!--links-->