Tiết 44:GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN - GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN Tiết 44:GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN - GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (705.89 KB, 15 trang )
<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1></div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>
<b>KIỂM TRA BÀI </b>
<b>CŨ</b>
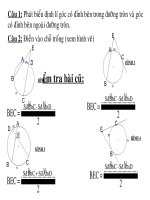
<b>B = </b> <b>sđ BC</b>
<b>2</b>
<b>A = </b> <b>sđ BC</b>
<b>2</b>
<b>O = sđ BC</b>
<b>Gọi tên và nêu cơng thức tính số đo của các góc </b>
<b>được ký hiệu trong mỗi hình vẽ sau:</b>
<i>H1</i> <i>H2</i> <i><sub>H3</sub></i>
<b>Đỉnh trùng </b>
<b>với tâm</b>
<b>Đỉnh thuộc </b>
<b>đường tròn</b>
<b>Đỉnh nằm trong </b>
<b>đường trịn</b>
</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>
<b>Tiết 44</b>
<b>GĨC CĨ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRỊN</b><b>GĨC CĨ ĐỈNH Ở BÊN NGỒI ĐƯỜNG TRỊN</b>
<b>1. Góc có đỉnh ở bên trong đường trịn:</b>
<b>Góc AEB là góc có đỉnh ở bên trong đường trịn, chắn hai cung AB và CD.</b>
</div>
<span class='text_page_counter'>(4)</span><div class='page_container' data-page=4>
<b>Tiết 44</b>
<b>GÓC CĨ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRỊN</b><b>GĨC CĨ ĐỈNH Ở BÊN NGỒI ĐƯỜNG TRỊN</b>
<b>1. Góc có đỉnh ở bên trong đường trịn:</b>
<b>Định lý: Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo </b>
<b>hai cung bị chắn.</b>
</div>
<span class='text_page_counter'>(5)</span><div class='page_container' data-page=5>
<b>Tiết 44</b>
<b>GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRỊN</b><b>GĨC CĨ ĐỈNH Ở BÊN NGỒI ĐƯỜNG TRỊN</b>
<b>1. Góc có đỉnh ở bên trong đường trịn:</b>
<b>Chứng minh</b> AEB = sđ AB + sđ CD
2
AEB là góc ngồi của EBD
AEB = sđ AB
2
sđ CD
2
<b>+</b>
</div>
<span class='text_page_counter'>(6)</span><div class='page_container' data-page=6>
<b>Tiết 44</b>
<b>GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRỊN</b><b>GĨC CĨ ĐỈNH Ở BÊN NGỒI ĐƯỜNG TRỊN</b>
<b>Nhận xét quan hệ về đỉnh, cạnh của góc F với đường trịn?</b>
<b>Góc F có: </b>
<b>+ Đỉnh nằm ngồi đường trịn.</b>
<b>+ Hai cạnh cắt đường trịn.</b>
</div>
<span class='text_page_counter'>(7)</span><div class='page_container' data-page=7>
<b>Tiết 44</b>
<b>GĨC CĨ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRỊN</b><b>GĨC CĨ ĐỈNH Ở BÊN NGỒI ĐƯỜNG TRỊN</b>
<b>2. Góc có đỉnh ở bên ngồi đường trịn:</b>
<b>m</b> <b>n</b>
<b>Số đo góc có đỉnh bên </b>
<b>ngồi đường trịn có quan </b>
<b>hệ gì với số đo các cung bị </b>
</div>
<span class='text_page_counter'>(8)</span><div class='page_container' data-page=8>
<b>Tiết 44</b>
<b>GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRỊN</b><b>GĨC CĨ ĐỈNH Ở BÊN NGỒI ĐƯỜNG TRỊN</b>
<i>Hình 1</i> <i>Hình 2</i> <i>Hình 3</i>
<b>2. Góc có đỉnh ở bên ngồi đường trịn:</b>
<b>Định lý: Số đo của góc có đỉnh bên ngồi đường trịn bằng nửa hiệu số </b>
<b>đo hai cung bị chắn.</b>
F = sđ CD - sđ AB
2
<b>m</b> <b>n</b>
F = sđ BC – sđ AB
2 F =
</div>
<span class='text_page_counter'>(9)</span><div class='page_container' data-page=9>
<b>Tiết 44</b>
<b>GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRỊN</b><b>GĨC CĨ ĐỈNH Ở BÊN NGỒI ĐƯỜNG TRỊN</b>
<b>2. Góc có đỉnh ở bên ngồi đường trịn:</b>
F = sđ CD - sđ AB
2
sđ CD
2
sđ AB
2
<b></b>
-F =
<b></b>
-F =
<b>Chứng minh:</b> F = sđ CD - sđ AB
2
CAD ADB
</div>
<span class='text_page_counter'>(10)</span><div class='page_container' data-page=10>
<b>Tiết 44</b>
<b>GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRỊN</b><b>GĨC CĨ ĐỈNH Ở BÊN NGỒI ĐƯỜNG TRỊN</b>
<i>Hình 1</i> <i>Hình 2</i> <i>Hình 3</i>
<b>2. Góc có đỉnh ở bên ngồi đường trịn:</b>
F = sđ CD - sđ AB
2 F =
sđ BC – sđ AB
2
<b>m</b> <b>n</b>
F = sđ AmB – sđ AnB
2
</div>
<span class='text_page_counter'>(11)</span><div class='page_container' data-page=11></div>
<span class='text_page_counter'>(12)</span><div class='page_container' data-page=12>
<b>Tiết 44</b>
<b>GĨC CĨ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRỊN</b><b>GĨC CĨ ĐỈNH Ở BÊN NGỒI ĐƯỜNG TRỊN</b>
<b>Bài tập áp dụng:</b>
Cho hình vẽChứng minh: AD BC.
Biết F = 500<sub>, sđ AB = 40</sub>0<sub>. Chứng minh: AD </sub><sub></sub><sub> BC</sub>
CHD = 900
Tính CD
F = sđ CD – sđ AB
2
</div>
<span class='text_page_counter'>(13)</span><div class='page_container' data-page=13>
<b>Hướng dẫn học ở nhà:</b>
- Học thuộc công thức tính góc có đỉnh ở bên trong, bên
ngồi đường trịn.
- Vẽ hình và chứng minh hai trường hợp còn lại của
định lý góc có đỉnh ở bên ngồi đường trịn.
</div>
<span class='text_page_counter'>(14)</span><div class='page_container' data-page=14>
<b>Bài 37/82 (sgk):</b>
Cho đường trịn (O) và hai dây AB, AC bằng
nhau. Trên cung nhỏ AC lấy một điểm M.
Gọi S là giao điểm của AM và BC.
Chứng minh: ASC = MCA.
MCA = sđ AM
2
ASC = sđ AB – sđ MC
2
sđ AB – sđ MC = sđ AM
sđ AB = sđ AC
<b>ASC = MCA</b>
</div>
<span class='text_page_counter'>(15)</span><div class='page_container' data-page=15>
<i>Xin cảm n qúy Thầy Cô </i>
<i><b>ơ</b></i>
</div>
<!--links-->