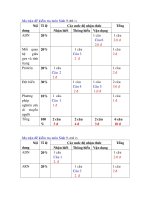
Ma trận đề kiểm tra Toán 8

KIỂM TRA HỌC KÌ I MÔN TOÁN 8. NĂM HỌC 2010 – 2011
I. MA TRẬN:
Nội dung Nhận biết Thông hiểu Vận dụng Tổng
TN TL TN TL TN TL
1) Chương 1 Đại số
Câu 1,8

1đ
Câu 2
0,5đ
Câu 1a
0,5đ
Câu 1a,5

1,5đ
6
3,5đ
2) Chương 2 Đại số
Câu 4,5,7

1,5đ
Câu 2a

0,5đ
Câu 2b
0,5đ
5

2,5đ
3) Chương 1 Hình học
Câu3,4a

2đ
Câu 4b

1đ
3

3đ
4) Chương 2 Hình học
Câu 3,6
1đ
2

1đ
Tổng
5

2,5đ
1

0,5đ
3

1,5đ
4

3đ
3

2,5đ
16

10đ
II. ĐỀ BÀI:
A. TRẮC NGHIỆM KHÁCH QUAN: (4 ĐIỂM)
Câu 1: Viết đa thức x
2
+ 6x + 9 dưới dạng bình phương của một tổng ta được kết quả nào
sau đây?
a) (x + 3)
2
b) (x + 5)
2
c) (x + 9)
2
d) (x + 4)
2
Câu 2: Phân tích đa thức: 5x
2
– 10x thành nhân tử ta được kết quả nào sau đây?
a) 5x(x – 10) b) 5x(x – 2) c) 5x(x
2
– 2x) d) 5x(2 – x)
Câu 3: Hình chữ nhật ABCD có AB = 8cm; BC = 5cm. Khi đó, diện tích hình chữ
nhật ABCD là:
a) 13cm
2
b) 40cm
2
c) 20cm
2

d) 3cm
2
Câu 4: Mẫu thức chung của hai phân thức
( )
x 1
x x 1
+
−
và
1
x 1−
là:
a)
( )
x x 1−
b)
( )
x x 1+
c)
x 1−
d)
x 1+
Câu 5: Phân thức đối của phân thức
2x 3
x
−
là phân thức nào?
a)
2 3x
x

−
b)
3x 2
x
−
c)
3 2x
x
−
d)
x
2x 3−
Câu 6: Cho ABC có BC = 3cm và đường cao AH = 4cm. Khi đó, diện tích
ABC là:
a) 7cm
2
b) 5cm
2
c) 6cm
2
d) 12cm
2
Câu 7: Phân thức nghịch đảo của phân thức
2
x 9
x 1
−
+
là phân thức nào?
a)

2
9 x
x 1
−
+
b)
2
x 1
x 9
−
−
c)
2
x 9
x 1
+
+
d)
2
x 1
x 9
+
−
Câu 8: Thực hiện phép chia 6x
4
y
2
:3xy ta được kết quả nào sau đây?
a) 18x
5

y
3
b) 9x
3
y c) 3x
3
y d) 2x
3
y
B. TỰ LUẬN: (6 ĐIỂM)
Câu 1: (1đ) Phân tích các đa thức sau thành nhân tử:
a) x
2
+ xy + 3x + 3y b) x
2
+ 2xy + y
2
– 9z
2
Câu 2: (1đ) Thực hiện phép tính:
a)
2x 5
2x 5 2x 5
−
− −
b)
( )
3
2
2

x 3
x 6x 9
:
3x 6x
−
− +
Câu 3: (1đ) Tứ giác ABCD có
µ
0
A 50=
;
µ
0
B 70=
;
µ
0
C 130=
. Tính số đo của góc D.
Câu 4: (2đ)
Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC,
CD, DA.
a) Chứng minh tứ giác EFGH là hình bình hành.
b) Tìm điều kiện của hai đường chéo AC và BD để tứ giác EFGH trở thành
hình vuông?
Câu 5: (1đ) Cho f(x) = (x
3
+ 2x
2
+ a); g(x) = (x + 1)

a) Thực hiện phép chia f(x) : g(x)
b) Tìm giá trị của a để f(x) chia hết cho g(x)
--------- Hết ---------
III. ĐÁP ÁN VÀ BIỂU ĐIỂM:
A. TRẮC NGHIỆM KHÁCH QUAN: (4 ĐIỂM)
Mỗi câu đúng được 0,5 điểm
Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8
a b b a c c d d
B. TỰ LUẬN: (6 ĐIỂM)
Câu 1: (1đ) Phân tích các đa thức sau thành nhân tử:
a) x
2
+ xy + 3x + 3y = x(x + y) + 3(x + y) = (x + y)(x + 3) (0,5đ)
b) x
2
+ 2xy + y
2
– 9z
2
= (x + y)
2
– (3z)
2
= (x + y + 3z)(x + y – 3z) (0,5đ)
Câu 2: (1đ) Thực hiện phép tính:
a)
−
− = =
− − −
2x 5 2x 5

1
2x 5 2x 5 2x 5
(0,25đ)
b)
( ) ( )
3 3
2
2 2 2
x 3 x 3
x 6x 9 6x
: .
3x 6x 3x x 6x 9
− −
− +
=
− +
(0,25đ)
( )
( )
3
2
2
x 3
6x
.
3x
x 3
−
=
−

(0,25đ)
( )
2 x 3
x
−
=
(0,25đ)
Câu 3: (1đ) Tứ giác ABCD có
µ
0
A 50=
;
µ
0
B 70=
;
µ
0
C 130=
. Tính số đo của góc D.
Ta có:
µ
µ µ
µ
0
A B C D 360+ + + =
(0,25đ)
µ
0 0 0 0
50 70 130 D 360+ + + =

(0,25đ)
µ
0 0 0 0
D 360 50 70 130= − − −
(0,25đ)
µ
0
D 110=
(0,25đ)
Câu 4: (2đ)
Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC,
CD, DA.
Vẽ hình đúng được (0,5đ)
a) Chứng minh tứ giác EFGH là hình bình hành.
EF là đường trung bình của ABC nên EF//=AC:2 (0,25đ)
HG là đường trung bình của ADC nên EF//=AC:2 (0,25đ)
Suy ra: EF = HG và EF//HG (0,25đ)
Suy ra: EFGH là hình bình hành (0,25đ)
b) Để tứ giác EFGH trở thành hình vuông thì AC
⊥
= BD (0,5đ)
Câu 5: (1đ) Cho f(x) = (x
3
+ 2x
2
+ a); g(x) = (x + 1)
a) Thực hiện phép chia f(x):g(x) (0,75đ)
x
3
+ 2x

2
+ a x + 1
–
x
3
+ x
2
x
2
+ x – 1
x
2
+ a
–
x
2
+ x
– x + a
–
– x – 1
a + 1
b) Để f(x) chia hết cho g(x) thì: a = – 1 (0,25đ)
---------- Hết ----------