Tài liệu Vị trí tương đối giữa mặt phẳng và mặt cầu ppt

§2.VÞ trÝ t−¬ng ®èi cña mét mÆt cÇu víi
mÆt ph¼ng vμ ®−êng th¼ng

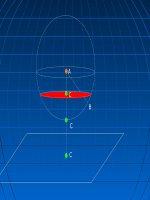
Mặt cầu (S) v mp(P) có một điểm chung duy nhất.

Khoảng cách từ tâm O của mặt cầu (S) tới mp(P) bằng bán kính của nó.

mp(P) vuông góc với một bán kính OH của mặt cầu (S) tại H.
* Đờng thẳng a tiếp xúc với mặt cầu S(O;R) khi v chỉ khi có một

Mặt cầu (S) v đờng thẳng a có một điểm chung duy nhất.

Khoảng cách từ tâm O của mặt cầu (S) tới đờng thẳng a bằng bán

Đờng thẳng a vuông góc với một bán kính OH của mặt cầu (S) tại H.
kính của mặt cầu.
trong các điều kiện sau:
một trong các điều kiện sau:
Kiểm tra kiến thức cũ
P
3. Các tính chất của tiếp tuyến
Định lý 1:
Qua điểm A nằm trên mặt cầu S(0;R) có vô
số tiếp tuyến của mặt cầu (S). Tất cả các tiếp tuyến ny
đều nằm trên tiếp diện của (S) tại điểm A.
CM: a A; a OA
Có vô số tiếp tuyến với (S) tại A
Các tiếp tuyến ny nằm trên mp(P):
mp(P) A, (P) OA
Đ2.Vị trí tơng đối của một mặt cầu với
mặt phẳng v đờng thẳng

A
O
a
mp(P) l tiếp diện của (S) tại A.
a l tiếp tuyến của S(O;R) tại A
* Đờng thẳng a tiếp xúc với mặt cầu S(O;R) khi v chỉ khi có một

Mặt cầu (S) v đờng thẳng a có một điểm chung duy nhất.

Khoảng cách từ tâm O của mặt cầu (S) tới đờng thẳng a bằng bán

Đờng thẳng a vuông góc với một bán kính OH của mặt cầu (S) tại H.
kính của mặt cầu.
trong các điều kiện sau:

Đờng thẳng a nằm trong mặt phẳng tiếp xúc với mặt cầu (S) v
đi qua điểm tiếp xúc.
Định lý 2: Qua điểm A nằm ngoi mặt cầu S(0;R) có vô số tiếp
tuyến với mặt cầu (S). Độ di các đoạn thẳng kẻ từ A tới các
tiếp điểm đều bằng nhau.
Khi (P) thay đổi vẫn đi qua AO thì có vô
số tiếp tuyến với (S) kẻ từ A.
Xét AMO: AM
2
= AO
2
-OM
2
= d
2

-R
2
22
RdAM =
Cm: Đặt OA = d d > R
Gọi (P) l mặt phẳng tuỳ ý đi qua AO;
mp(P) S(O;R) = C(O;R).
Vì A nằm ngoi (S) nên A nằm ngoi (C).
Qua A kẻ 2 tiếp tuyến AM v AM với (C),
M
M
(C)
P
A
0
Vậy các đoạn thẳng kẻ từ A tới các tiếp
điểm đều bằng nhau.
đó l 2 tiếp tuyến của (S).