Tài liệu Bài giảng Vật lý_ doc

1
Chương III:
Chương III:
HI
HI
ỆN TƯỢNG GIAO THOA
ỆN TƯỢNG GIAO THOA
& NHIỄU XẠ ÁNH SÁNG
& NHIỄU XẠ ÁNH SÁNG




2
Nội dung
Nội dung
HIỆN TƯỢNG GIAO THOA ÁNH SÁNG
HIỆN TƯỢNG GIAO THOA ÁNH SÁNG
1.
1.
Hiện
Hiện


tượng
tượng


giao
giao

thoa
thoa


và
và


điều
điều


kiện
kiện


để
để


có
có


giao
giao


thoa

thoa


ánh
ánh


sáng
sáng


2.
2.
Khảo
Khảo


sát
sát


sự
sự


giao
giao


thoa

thoa


ánh
ánh


sáng
sáng
qua
qua
khe
khe
Young
Young
SỰ NHIỄU XẠ ÁNH SÁNG
SỰ NHIỄU XẠ ÁNH SÁNG
3.
3.
Thí
Thí


nghiệm
nghiệm


Fresnel
Fresnel

về
về


nhiễu
nhiễu


xạ
xạ


ánh
ánh


sáng
sáng
4.
4.
Định
Định


nghĩa
nghĩa
5.
5.
Nguyên

Nguyên


lý
lý


Huyghen
Huyghen
–
–
Fresnel
Fresnel
6.
6.
Nhiễu
Nhiễu


xạ
xạ


ánh
ánh


sáng
sáng
qua

qua
khe
khe


hẹp
hẹp
(
(
nhiễu
nhiễu


xạ
xạ


sóng
sóng


phẳng
phẳng
): (
): (
Nhiễu
Nhiễu


xạ

xạ


Frauhofe
Frauhofe
)
)
7.
7.
Điều
Điều


kiện
kiện


để
để


có
có


cực
cực


đại

đại
,
,
cực
cực


tiểu
tiểu


nhiễu
nhiễu


xạ
xạ


8.
8.
Nhiễu
Nhiễu


xạ
xạ
qua
qua
nhiều

nhiều


khe
khe


hẹp
hẹp
–
–
cách
cách


tử
tử
3
1.a
1.a
Định nghĩa
Định nghĩa
Là hiện tượng xãy ra khi
Là hiện tượng xãy ra khi
2 sóng ánh sáng truyền đến
2 sóng ánh sáng truyền đến
một vùng nào đó của không
một vùng nào đó của không
gian, ở đó tạo ra vùng sáng
gian, ở đó tạo ra vùng sáng

và tối liên tiếp.
và tối liên tiếp.
Khoảng
Khoảng
không gian có giao thoa gọi
không gian có giao thoa gọi
là trường giao thoa. Nếu đặt
là trường giao thoa. Nếu đặt
một màng trong trường giao
một màng trong trường giao
thoa ta sẽ nhận được những
thoa ta sẽ nhận được những
vạch sáng và tối xen kẽ gọi
vạch sáng và tối xen kẽ gọi
là vân giao thoa.
là vân giao thoa.
F
F
E
E
S
S
4
1.b
1.b
Điều kiện để có giao thoa ánh sáng
Điều kiện để có giao thoa ánh sáng
2 s
2 s
óng ánh sáng (nguồn) phải có cùng tần

óng ánh sáng (nguồn) phải có cùng tần
số, phương dao động, hiệu pha không thay đổi
số, phương dao động, hiệu pha không thay đổi
theo thời gian.
theo thời gian.
Giả sử xét nguồn 1:
Giả sử xét nguồn 1:
nguồn 2:
nguồn 2:
Theo 2 dao động
Theo 2 dao động
Trong đó
Trong đó
: Hiệu pha
: Hiệu pha
1 1 0 1
cos( )x a t
ω ϕ
= +
2 2 0 2
cos( )x a t
ω ϕ
= +
1 2 0
cos( )x x x a t
ω ϕ
= + = +
2 2
1 2 1 2 2 1
2 cos( )a a a a a

ϕ ϕ
= + + −
2 1
ϕ ϕ
−
5
1.b
1.b
Điều kiện để có giao thoa ánh sáng
Điều kiện để có giao thoa ánh sáng
N
N
ếu:
ếu:
Cho:
Cho:
Để đặc trưng tác dụng sóng của sóng ánh sáng, ta
Để đặc trưng tác dụng sóng của sóng ánh sáng, ta
đưa vào cường độ sóng cơ.
đưa vào cường độ sóng cơ.
Chọn k=1, cường độ sáng
Chọn k=1, cường độ sáng
I
I
~ a
~ a
2
2
=>
=>

I
I
~ 4a
~ 4a
1
1
2
2


(Cường độ sóng tỉ lệ bình phương với biên độ của sóng).
(Cường độ sóng tỉ lệ bình phương với biên độ của sóng).
Như vậy, những điểm nhận 2 sóng có
Như vậy, những điểm nhận 2 sóng có
I
I
~ 4a
~ 4a
1
1
2
2
là
là
điểm sáng.
điểm sáng.
1 1 2 2
1 1 2 2
sin sin
cos cos

a a
tg
a a
ϕ ϕ
ϕ
ϕ ϕ
+
=
+
2 1 2 1
2 cos( ) 1k
ϕ ϕ π ϕ ϕ
− = ⇒ − =
1 2
a a a= +
1 2 1 2
2 2a a a a a≈ ⇒ ≈ ≈
6
1.b
1.b
Điều kiện để có giao thoa ánh sáng
Điều kiện để có giao thoa ánh sáng
N
N
ếu:
ếu:


mà
mà

Điểm tối
Điểm tối
2 sóng có điều kiện trên gọi là 2 sóng kết
2 sóng có điều kiện trên gọi là 2 sóng kết
hợp.
hợp.
Chú ý:
Chú ý:
Trong môi trường đẳng hướng, sóng ánh
Trong môi trường đẳng hướng, sóng ánh
sáng từ S phát ra là sóng cầu, biên độ của sóng sẽ
sáng từ S phát ra là sóng cầu, biên độ của sóng sẽ
giảm tỉ lệ nghịch với khoảng cách từ nguồn đến
giảm tỉ lệ nghịch với khoảng cách từ nguồn đến
điểm ta xét.
điểm ta xét.
2 1 2 1
(2 1) cos( ) 1k
ϕ ϕ π ϕ ϕ
− = + ⇒ − = −
1 2
a a a= −
1 2
0a a a≈ ⇒ =
7
1.c
1.c
Cách tạo nguồn kết hợp

Cách tạo nguồn kết hợp
Nguồn sóng biến thiên do dao động của các
Nguồn sóng biến thiên do dao động của các
nguyên tử, do đó không tìm được sóng kết hợp từ
nguyên tử, do đó không tìm được sóng kết hợp từ
2 nguồn sáng. Để có sóng kết hợp, ta tách từ 1
2 nguồn sáng. Để có sóng kết hợp, ta tách từ 1
nguồn sáng thành 2 tia sóng đi theo những quang
nguồn sáng thành 2 tia sóng đi theo những quang
lộ khác nhau. Sau đó, cho chúng gặp mhau.
lộ khác nhau. Sau đó, cho chúng gặp mhau.
8
1.c
1.c
Cách tạo nguồn kết hợp
Cách tạo nguồn kết hợp



G
G
ương Fresnel:
ương Fresnel:


α
O
O
Q
Q

G
G
1
1
O
O
1
1
O
O
2
2
G
G
2
2
E
E
Maøn chaén
9
1.c
1.c
Cách tạo nguồn kết hợp
Cách tạo nguồn kết hợp



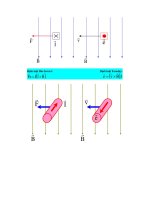
Lưỡng bán thấu kính
Lưỡng bán thấu kính
G.Bille:

G.Bille:



Lưỡng lăng kính
Lưỡng lăng kính
Fresnel:
Fresnel:
S
S
M
M
M
M
S
S
10
2.a
2.a
Điều kiện cực đại cực tiểu vân giao thoa
Điều kiện cực đại cực tiểu vân giao thoa
Gi
Gi
ả sử có 2 nguồn sóng kết hợp S
ả sử có 2 nguồn sóng kết hợp S
1
1
và S
và S
2

2
Đặt: S
Đặt: S
1
1
M =
M =
l
l
1
1
và S
và S
1
1
M =
M =
l
l
2
2
(quang lộ)
(quang lộ)
M nhận 2 sóng:
M nhận 2 sóng:
1
1 1 0
2
cos( )
l

x a t
π
ω
λ
= −
2
2 2 0
2
cos( )
l
x a t
π
ω
λ
= −
11
2.a
2.a
Điều kiện cực đại cực tiểu vân giao thoa
Điều kiện cực đại cực tiểu vân giao thoa
dao động cực đại
dao động cực đại
cường độ sóng đạt cực đại :I
cường độ sóng đạt cực đại :I
max
max
Nếu:
Nếu:
dđ cực tiểu
dđ cực tiểu

Những điểm có cường độ sáng tối nhất:
Những điểm có cường độ sáng tối nhất:
I
I
min
min
= 0.
= 0.
2 1 2 1
2
( )l l
π
ϕ ϕ ϕ
λ
∆ = − = −
2k
ϕ π
∆ =
2 1
l l k
λ
− =
2 1
(2 1) (2 1)
2
k l l k
λ
ϕ π
∆ = + ⇒ − = +
12

2.b
2.b
Độ rộng của vân giao thoa
Độ rộng của vân giao thoa
Là khoảng cách giữa 2 vân cùng loại liên
Là khoảng cách giữa 2 vân cùng loại liên
tiếp. Cọn O là điểm cách đầu S
tiếp. Cọn O là điểm cách đầu S
1
1
, S
, S
2
2
:
:
Thông thường:
Thông thường:
2 2 2
1
( )
2
d
l D x= + −
2 2 2
2
( )
2
d
l D x= + +

2 2
2 1 2 1
2 1
2
2
xd
l l xd l l
l l
− = ⇒ − =
+
2 1
2D d l l D⇒ + ≈?
2 1
xd
l l
D
− =
13
2.b
2.b
Độ rộng của vân giao thoa
Độ rộng của vân giao thoa
Vậy các cực đại giao thoa sẽ nằm cách điểm
Vậy các cực đại giao thoa sẽ nằm cách điểm
giữa O một khoảng X
giữa O một khoảng X
max
max
thỏa mãn điều kiện:
thỏa mãn điều kiện:

Cực tiểu:
Cực tiểu:
max
2 1
x d
l l k
D
λ
− = =
min
(2 1)
2
x d
k
D
λ
+ =
min
(2 1)
2
k D
x
d
λ
+
=
0, 1, 2,...k = ± ±
max
k D
x

d
λ
=
14
2.b
2.b
Độ rộng của vân giao thoa
Độ rộng của vân giao thoa
Khoảng cách giữa các vân sáng
Khoảng cách giữa các vân sáng
(hoặc giữa các vân tối cũng vậy)
(hoặc giữa các vân tối cũng vậy)
max max
( 1) ( )i x k x k= + −
( 1)
D k D
k
d d
λ λ
= + −
D
i
d
λ
⇒ =
M
M
S
S
1

1
S
S
2
2
d
d
l
l
2
2
D
D
l
l
1
1
S
S