Ôn tập hình học 9 thi vào lớp 10

LUYỆN TẬP ø TIẾP TUYẾN
1/ Cho (O,R) đường kính AB, tiếp tuyến Bx, trên Bx lấy BM=R, kẻ tiếp tuyến MC, AM cắt
(O) tại E.
a) Chứng minh: OCMB là hình vuông
b) Chứng minh:MA.ME= R
2

c) Chứng minh:
∆
CME ~
∆
AMC
d) Tính độ dài CE và S
OEB
theo R
2/ Cho (O,R) đường kính BC, kẻ dây AD vuông góc OB tại trung điểm của OB> Vẽ BM,
CN là tiếp tuyến của (A) (M và N là tiếp điểm).
a) Chứng minh:OBAC là hình thoi.
b) Chứng minh:BM + NC = BC.
c) Chứng minh:M, A, N thẳng hàng.
d) Tính S
BMNC
theo R
3/ Cho nửa(O) đường kính AB, C thuộc (O), kẻ OH vuông góc BC, OH cắt tiếp tuyến tại B
ở E. Gọi D là giao điểm của OE với (O), M là giao điểm của AD với BC.
a) Chứng minh:
EBABCA
ˆ
ˆ
=
và H là trung điểm của BC.

b) Chứng minh: AD là phân giác của
BAC
ˆ
.
c) Chứng minh: EC là tiếp tuyến của (O).
d) AD cắt BE tại I, IH cắt BD tại K. Chứng minh: KH.BI=IK.BH
4/ Cho AB và AC là 2 tiếp tuyến của(O,R) . Kẻ đường kính CM, kẻ OH vuông góc BC tại
H, AM cắt (O) tại N.
a) Chứng minh:
BCACBA
ˆ
ˆ
=
b) Chứng minh: O, H, A thẳng hàng.
c) Chứng minh: AB
2
=AM.AN.
d) Chứng minh:
OMANHA
ˆˆ
=
.
e) Biết OA= 3R. Tính BC và S
AOM
theo R.
5/ Cho (O) đường kính AB, kẻ bán kính OI vuông góc BC tại H, gọi M là giao điểm của
BC và AI. Vẽ (I) bán kính IB,AC cắt (I) tại K.
a) Chứng minh: H là trung điểm của BC.
b) Chứng minh: AI là phân giác của
BAC

ˆ
.
c) Chứng minh: B, I, K thẳng hàng.
d) Gọi E là trung điểm của AM, chứng minh: CE là tiếp tuyến của (I)
6/ Cho (O,R) đường kính AB,Trên tiếp tuyến tại A lấy AD=2R, trên (O) lấy điểm C sao
cho AD = DC . vẽ (I) đường kính OA cắt AC tại M.
a) Chứng minh: hai đường tròn tâm O và I tiếp xúc.
b) Chứng minh: OM // BC và 3 điểm O, M, D thẳng hàng.
c) Chứng minh: DC là tiếp tuyến của (O).
d) Kẻ AI // OC ( I thuộc AD). Chứng minh: AOCI là hình thoi và tính S
AOCI
theo R.
7/ Cho (O,R) đường kính AB, tiếp tuyến Ax, trên Ax lấy điểm M sao cho OM=2R, kẻ tiếp
tuyến MC, kẻ CH vuông góc AB và OK vuông góc AC. Tiếp tuyến tại B cắt AC tại D
a) Chứng minh: O, K, M thẳng hàng.
b) Chứng minh: AC.AD = 4R
2
.
c) Kẻ CE vuông góc AM cắt OM tại P. Chứng minh: OCPA là hình thoi.
d) Gọi I làtrung điểm của CH, AI cắt BD tại N. Chứng minh: CN là tiếp tuyến của(O).
8/ Cho (O) đk AB, dây AC < CB.Tia phân giác
COA
ˆ
cắt tiếp tuyến ở A tại M, kẻ CH
vuông góc AB.
a) Chứng minh: MC là tiếp tuyến của (O).
b) Chứng minh: OM // BC.
c) OM.CH = MC.BC
d) Gọi I là giao điểm của CH và MB. Chứng minh: I là trung điểm của CH.
9/ Cho (O) đường kính AB, lấy C thuộc (O), kẻ bán kính OI // AC , BI cắt AC tại D, AI cắt

tiếp tuyến ở B tại O’. Vẽ (O’) bán kính O’B .
a) Chứng minh: O’B
2
=O’A.O’I
b) Chứng minh:AO’ là phân giác
BAD
ˆ
.
c) Chứng minh: AD là tiếp tuyến của (O’).
d) Kẻ dây cung EF của (O’) đi qua I. Chứng minh: IE.AF = IF.AE
10/ Cho (O) đường kính AB, dây cung AD > DB, kéo dài AD một đoạn DM = AD. BM cắt
(O) tại C, gọi H là giao điểm của AC và BD.
a) Chứng minh:AB = BM.
b) Chứng minh: AH.BC = HC.AB.
c) Chứng minh:MH vuông góc AB tại I.
d) Chứng minh: AC.AH + BH.BD = 4R
2
.
e) Gọi K là trung điểm MH. Chứng minh: DK là tiếp tuyến của(O).
11/ Cho
∆
ABC có 3 góc nhọn , vẽ (O) đường kính BC cắt AB và AC tại M và N. Gọi H là
giao điểm của BN và CM.
a) Chứng minh: AH vuông góc BC tại D.
b) Chứng minh: 4 điểm B, M, H, D cùng thuộc 1 đường tròn, xác đònh tâm K của
đường tròn này.
c) Chứng minh: AH.AD + BH.BN = AB
2
.
d) Chứng minh: hai tiếp tuyến tại M và N cùng gặp nhau tại 1 điểm trên AH.

I Gãc ë t©m – liªn hƯ gi÷a cung vµ d©y.
Bµi 1. Cho hai ®êng trßn (O) vµ (O’) c¾t nhau t¹i hai ®iĨm A, B. D©y AC cđa ®êng trßn (O) vu«ng
gãc víi AO’; d©y AD cđa ®êng trßn (O’) vu«ng gãc víi AO. So s¸nh c¸c gãc
¼
¼
AOD , AO'D
.
Bài 2. Trên một đờng tròn (O) có cung
ằ
AB
bằng 140
o
. Gọi A. B lần lợt là đối xứng của A, B
qua O; lấy cung
ằ
AD
nhận B làm điểm chính giữa; lấy cung
ằ
CB
nhận A làm điểm chính giữa.
Tính số đo cung nhỏ
ằ
CD
.
Bài 3. Cho hai đờng tròn bằng nhau (O) , (O) cắt nhau tại A, B. Kẻ các đờng kính AOC và AOD.
Gọi E là giao điểm thứ hai của đờng thẳng AC với (O).
a) So sánh các cung nhỏ
ằ
CB
,

ằ
BD
.
b) Chứng minh rằng B là điểm chính giữa cung
ẳ
EBD
.
Bài 4. a) Cho đờng tròn (O, R) với hai điểm A, B. Tìm quỹ tích trung điểm của các dây trên đờng
tròn có độ dài bằng dây AB.
b) Cho đờng tròn (O, R) với hai tiếp tuyến AB, AC. Một tiếp tuyến di động của đờng tròn
(O) cắt các đoạn thẳng AB, AC tại các điểm tơng ứng P, Q. Gọi P, Q theo thứ tự là giao điểm
của các đoạn thẳng OP, OQ với đờng tròn (O). Chứng minh rằng cung nhỏ
ẳ
P'Q'
có số đo
không đổi. Tìm quỹ tích trung điểm I của PQ.
Bài 5. Cho đờng tròn (O), dây AB. Gọi M là điểm chính giữa cung
ằ
AB
. Vẽ dây MC cắt dây AB
tại D. Vẽ đờng vuông góc với AB tại D, cắt OC tại K.
KCDV
là tam giác gì ?
Bài 6. Cho M, N, P, Q là bốn điểm tùy ý trên đờng tròn (O). Các tiếp tuyến của (O) tại bốn điểm
trên cắt nhau tạo thành tứ giác ABCD. Tính số đo tổng các góc
AOB + COD
?
Bài 7. Cho đờng tròn (O), dây AB. Trên dây AB lấy D rồi nối D với C trên đờng tròn (C khác A,
B; A, O, C không thẳng hàng). Các đờng trung trực của AD và DC cắt nhau ở M. CMR: đờng
thẳng MO đi qua điểm chính giữa cung

ằ
AC
.
Bài 8. Cho hai đờng tròn đồng tâm (O;R) và (O;2R). P là một điểm ngoài (O;2R). Vẽ đờng tròn
(P;PO) cắt đờng tròn (O;2R) tại C và D, cắt đờng tròn (O;R) ở E và F. OC và OD cắt (O;R) ở
A và B. CMR:
a) CD // EF.
b) PA và PB là hai tiếp tuyến của (O;R).
Bài 9. Cho hình thoi ABCD có cạnh AB =5 cm và đờng chéo AC=8 cm. Đờng tròn tâm A bán
kính R=5 cm tiếp xúc với đờng tròn tâm C tại M thuộc đoạn AC. Đờng tròn này cắt CB tại E
và cắt CD tại F. Tính tỉ số độ dài của cung
ằ
BD
và cung
ằ
EF
II góc nội tiếp.
Bài 10. Cho góc xOy bằng x và một độ dài l . Hai điểm A,B di động trên hai cạnh tơng ứng sao cho
độ dài AB luôn bằng l . Gọi I là tâm đờng tròn ngoại tiếp tam giác OAB.
a) CMR: Tam giác IAB có các kích thớc không đổi.
b) Tìm quỹ tích điểm I.
Bài 11. Cho hai đờng tròn (O) và (O) cắt nhau tại A, B. Qua A kẻ cát tuyến cắt các đờng tròn (O),
(O) tại các điểm thứ hai C, D. Tia DB cắt (O) tại điểm thứ hai là M. Các tia OB, BO lần lợt
cắt (O) tại các điểm thứ hai là N, P.
a) So sánh hai góc
ACB
và
BOO'
.
b) So sánh hai góc

CAM
và
PAN
.
Bài 12. Cho hai đờng tròn (O) và (O) cắt nhau tại A, B. Hai dây AC và BD cắt nhau ở I và cắt (O)
tại C, D. Chứng minh rằng CD // CD.
Bài 13. Cho tam giác ABC nội tiếp (O), các đờng cao AD, BE, CF đồng quy tại H. Các tia AD, BE,
CF cắt (O) tại các điểm thứ hai tơng ứng A, B, C.
a) CMR: AB, BC, CA là trung trực của các đoạn thẳng tơng ứng HC, HA, HB.
b) CMR: H là tâm đờng tròn nội tiếp tam giác DEF.
c) CMR: Tam giác ABC đồng dạng với tam giác DEF. Từ đó so sánh bán kính đờng tròn
ngoại tiếp tam giác DEF và bán kính đờng tròn (O).
Bài 14. Cho góc vuông xOy vuông, điểm A cố định trên Ox, một điểm B di động trên cạnh Oy.
Trên nửa mặt phẳng bờ AB không chứa O ngời ta vẽ hình vuông ABCD tâm I. Tìm quỹ tích
điểm I.
Bài 15. Cho đờng thẳng d và đoạn thẳng AB cắt nhau tại C. Dựng điểm M trên d sao cho MC là
phân giác góc
AMB
.
Bài 16. Cho hai đờng tròn (O) và (O) tiếp xúc với nhau tại A. Qua A vẽ một cát tuyến cắt (O) tại
B, cắt (O) tại C. Một cát tuyến thứ hai qua A cắt (O) tại D, cắt (O) tại E. Chứng minh rằng
CE // BD.
Bài 17. Cho nửa đờng tròn đờng kính AB. Gọi O là điểm chính giữa cung
ằ
AB
và M là một điểm
bất kì của nửa đờng tròn đó. Tia AM cắt đờng tròn (O;OA) tại điểm thứ hai là N. Chứng
minh rằng MN = MB.
Bài 18. Cho đờng tròn tâm O đờng kính AB và một điểm C chạy trên một nửa đờng tròn. Vẽ đờng
tròn (I) tiếp xúc với (O) tại C và tiếp xúc với đờng kính AB tại D, đờng tròn này cắt CA, CB

lần lợt tại các điểm thứ hai là M, N. CMR:
a) Ba điểm M, I, N thẳng hàng.
b) ID MN.
c) Đờng thẳng CD đi qua một điểm cố định.
d) Suy ra cách dựng đờng tròn (I) nói trên.
Bài 19. Cho (O), đờng kính AB, điểm D thuộc đờng tròn. Gọi E là điểm đối xứng với A qua D.
a) Tam giác ABE là tam giác gì ?
b) Gọi K là giao điểm của EB với (O). Chứng minh rằng OD AK.
Bài 20. Cho hai đờng tròn (O) và (O) cắt nhau ở A, B, O nằm trên (O). Dây AC của (O) cắt (O)
ở D, dây OE của (O) cắt (O) ở F. Chứng minh :
a) OD BC.
b) Điểm F cách đều ba cạnh của tam giác ABE.
Bài 21. Cho hai đờng thẳng song song. Một đờng tròn tiếp xúc với một đờng thẳng tại A và cắt đ-
ờng thẳng kia tại B, C. Trên đờng tròn lấy một điểm D ( không trùng A, B, C ). Chứng minh
rằng A cách đều hai đờng thẳng BD và CD.
Bài 22. MA và MB là hai tiếp tuyến của (O). Vẽ (M;MA), C là một điểm nằm trên cung AB của
(M) ( cung AB nằm trong đờng tròn (O) ). Tia AC, BC cắt (O) ở P, Q. Chứng minh rằng : P
và Q đối xứng với nhau qua O.
Bài 23. Trên cạnh CD của hình vuông ABCD ta lấy một điểm M khác C, D. Các đờng tròn đờng
kính CD và AM cắt nhau tại điểm thứ hai N ( khác D ). Tia DN cắt BC tại P. Chứng minh
rằng: AC PM.
III góc giữa tiếp tuyến và một dây.
Bài 24. Hai tiếp tuyến tại A và B của đờng tròn (O
1
) cắt nhau tại C. Vẽ đờng tròn (O
2
) đi qua C,
tiếp xúc với đờng thẳng AB tại B và cắt đờng tròn (O
1
) ở M. Chứng minh rằng đờng thẳng

AM chia đoạn BC thành hai phần bằng nhau.
Bài 25. Cho hai đờng tròn (O;R) và (O;r) với R > r tiếp xúc trong tại A. Dây BC của (O;R) tiếp
xúc với (O;r) tại M ( ba điểm o, A, M không thẳng hàng ). Chứng minh rằng tia AM là phân
giác của góc
BAC

.
Bài 26. Cho nửa đờng tròn tâm O đờng kính EF. Vẽ đờng tròn (O) tiếp xúc trong với nửa đờng
tròn tâm O tại A. Kẻ đờng thẳng vuông góc với EF cắt nửa đờng tròn tâm O tại B và tiếp xúc
với (O) tại M. Chứng minh rằng tia AM đI qua một đầu của đờng kính EF.
Bài 27. Cho ABC vuông tại A, đờng cao AH. Vẽ đờng tròn tâm I đờng kính BH, nó cắt AB ở M.
Vẽ đờng tròn tâm K đờng kính CH, nó cắt AC tại N.
a) Tứ giác AMHN là hình gì ?
b) CMR: MN là tiếp tuyến chung của hai đờng tròn (I) và (K).
c) Vẽ tiếp tuyến Ax của đờng tròn ngoại tiếp ABC. CMR: Ax // MN.
Bài 28. Cho hai đờng tròn (O) và (O) cắt nhau tại B, C. Tiếp tuyến tại C của đờng tròn (O) cắt
(O) tại điểm thứ hai là M. Vẽ cát tuyến MBA ( A thuộc đờng tròn tâm O ). Từ M vẽ tiếp
tuyến xy của đờng tròn (O). CMR:
a) MC
2
= MA.MB
b) AC // xy.
Bài 29.Cho hai đờng tròn (O) và (O) cắt nhau tại A, B. Vẽ dây BC của (O) tiếp xúc với (O). Vẽ
dây BD của (O) tiếp xúc với (O). CMR:
a) AB
2
= AC.AD
b)
BC AC
BD AD

=
.
Bài 30.Cho ABC ngoại tiếp đờng tròn (O). Gọi D, E, F là các tiếp điểm trên các cạnh AB, BC,
CA. Gọi M, N, P lần lợt là giao điểm của (O) với các tia OA, OB, OC. Chứng minh rằng các
điểm M, N, P lần lợt là tâm của các đờng tròn nội tiếp các tam giác ADF, BDE và CEF.
Bài 31.Cho hai đờng tròn (O) và (O) cắt nhau ở A, B. Một đờng thẳng tiếp xúc với (O) tại C và
tiếp xúc với (O) tại D. Vẽ đờng tròn (I) qua ba điểm A, C, D cắt đờng thẳng AB tại điểm thứ
hai là E. CMR:
a) CAD + CBD = 180
o
.
b) Tứ giác BCED là hình bình hành.
Bài 32.Cho đờng tròn (O) và một điểm M ở bên ngoài đờng tròn. Tia Mx quay quanh M cắt (O)
tại A, B. Gọi I là một điểm trên Mx sao cho MI
2
= MA.MB. Tìm quỹ tích của I.
Bài 33.Cho đờng tròn (O) ngoại tiếp ABC. Gọi I và J lần lợt là giao điểm của hai phân giác
trong và ngoài của góc B và góc C của ABC. Đờng thẳng IJ cắt (O) tại M.
a) CMR: MBI = BIM.
b) Bốn điểm I, B, J, C cùng nằm trên một đờng tròn.
Bài 34.Cho điểm A cố định trên đờng tròn cố định tâm O. Một góc xAy = x không đổi quay
quanh A, Ax cắt (O) tại B, Ay cắt (O) tại C. Các đờng thẳng qua B và C lần lợt vuông góc với
Ay và Ax, cắt (O) theo thứ tự tại P và Q.
a) Chứng minh P, Q cố định.
b) Tìm tập hợp những điểm H là giao của BP và CQ.
Bài 35.Cho ABC cân tại A và một dây di động AM của đờng tròn ngoại tiếp tam giác ấy. Đờng
thẳng qua B, vuông góc với AM tại A, cắt CM tại P.
a) Chứng tỏ DMB = BMP.
b) Chứng minh P thuộc đờng tròn cố định.
IV góc có đỉnh bên trong-bên ngoài đ ờng tròn.

Bài 36. Cho ABC nội tiếp (O), Các tia phân giác của góc A và góc B cắt nhau tại I và cắt (O)
theo thứ tự tại M và N
a) Chứng minh :
ẳ
ẳ
MB MC=
,
ằ
ằ
NA NC=
.
b) Chứng minh : MB = MI = MC.
c) Gọi k là điểm đối xứng với I qua M. CMR: K là tâm đờng tròn bàng tiếp ABC.
Bài 37.Cho đờng tròn (O), đờng kính AB vuông góc với dây CD. Qua M thuộc cung
ằ
AD
kẻ tiếp
tuyến với đờng tròn cắt CD tại I. Gọi E là giao điểm của BM và CD.
a) Chứng minh rằng : IM = IE.
b) Gọi F là giao điểm của AM và CD. Chứng minh rằng AFC= ABM.
Bài 38.Từ một điểm A bên ngoài đờng tròn (O) ta vẽ tiếp tuyến AB và cát tuyến ACD. Vẽ dây BM
vuông góc với tia phân giác của góc BAC, dây này cắt CD tại E. Chứng minh rằng :
a) Tia BM là phân giác của góc CBD.
b) MD
2
= ME.MB
Bài 39. Ba điểm A, B, C thuộc đờng tròn tâm O sao cho tiếp tuyến tại A cắt tia BC tại D. Tia phân
giác của góc BAC cắt đờng tròn ở M, tia phân giác của góc D cắt AM ở I. Chứng minh DI
AM.
Bài 40. Cho ABC cân tại B. Qua B kẻ đờng thẳng xy song song với AC. Gọi O là một điểm trên

xy. Vẽ đờng tròn tâm O tiếp xúc với AC ở D, cắt các cạnh AB và BC ở E và F. Chứng minh
rằng số đo cung
ẳ
EDF
không đổi khi O di chuyển trên xy.
Bài 41. Cho ABC nội tiếp (O). Gọi CM, AN, BP lần lợt là các phân giác của ABC chúng giao
nhau tại I. MN cắt AB tại E.
a) BNI là tam giác gì ?
b) CMR: AE.BN = EB.AN
c) CMR: EI // BC.
d) Gọi D là giao của AN và BC. CMR:
AN AB
BN BD
=
Bài 42.Cho hình thang vuông ABCD ( BC // AD ). Trên AB lấy hai điểm M, N sao cho M, N nhìn
CD dới các góc vuông. CMR: S
ABCD
= S
MCD
+ S
NCD
.
Bài 43. Cho các điểm A
1
, A
2
, , A
19
, A
20

đợc sắp xếp theo thứ tự đó trên cùng một đờng tròn (O).
Chúng chia đờng tròn thành 20 cung bằng nhau. Chứng minh rằng dây A
1
A
8
vuông góc với
dây A
3
A
16
.
Bài 44. Cho ABC nội tiếp trong đờng tròn (O); A
1
, B
1
, C
1
là các điểm đối xứng của A, B, C qua
O; A
0
, B
0
, C
0
là trung điểm các cạnh BC, CA, và AB tơng ứng. CMR: A
1
A
0
, B
1

B
0
, C
1
C
0

đồng quy.
Bài 45. Cho ABC nội tiếp trong (O). D là điểm chính giữa cung BC. Một đờng tròn thay đổi đi
qua A và D cắt các đờng thẳng AB, BD, AC theo thứ tự E, F, G. Chứng minh :
a) D là điểm chính giữa cung
ằ
EG
.
b) EF luôn song song với một đờng thẳng cố định.
Bài 46. Cho góc nhọn xAy, lấy B và C trên Ax và Ay. Dựng đờng tròn qua B và C cắt Ax tại P, Ay
tại Q sao cho PQ = m ( m là độ dài cho trớc ).
Bài 47. Cho hai đờng tròn (O) và (O) tiếp xúc ngoài tại A. Gọi TT' là tiếp tuyến chung ngoài của
(O) và (O), T và T là các tiếp điểm tơng ứng của (O) và (O). Đờng thẳng OO cắt (O) tại B
(khác A) và cắt (O) tại C (khác A). BT cắt CT tại D. Chứng minh BCD và ATT đồng
dạng.
Bài 48. Cho ABC nhọn ; các chân đờng cao xuất phát từ A, B, C trên các cạnh BC, CA, AB là D,
E, F. Chứng minh rằng trực tâm ABC trùng với tâm dờng tròn nội tiếp DEF.
Bài 49.Cho ABC nội tiếp (O). BD và CE là hai đờng cao xuất phát từ B và C. (d) là tiếp tuyến
của (O) tại A. CMR: d // DE.
V cung chứa góc.
Bài 50. Cho ABC nội tiếp (O). D là một điểm chuyển động trên cung BC không chứa A. Nối A
với D. Kẻ CH vuông góc với AD. Tìm quỹ tích điểm H.
Bài 51. Cho BC là một dây cung cố định của (O), A là một điểm chạy trên cung lớn BC sao cho
ABC luôn có ba góc nhọn. Gọi M là điểm chính giữa cung nhỏ BC của (O). Tìm quỹ tích

trung điểm I của AM.
Bài 52. Cho nửa đờng tròn đờng kính AB và cung
ằ
EF
của nửa đờng tròn (E nằm trên cung
ằ
AF
)
sao cho số đo cung
ằ
EF
= 60
0
.Hai tia AE và BF cắt nhau tại M. Tìm quỹ tích các điểm M khi
cung
ằ
EF
di chuyển trên nửa đờng tròn.
Bài 53. Cho ABC vuông tại A. Vẽ hai nửa đờng tròn đờng kính AB và AC ra phía ngoài tam
giác. Qua A vẽ cát tuyến MAN (M thuộc nửa đờng tròn đờng kính AB, N thuộc nửa đờng
tròn đờng kính AC).
a) Tứ giác BMNC là hình gì ?
b) Tìm quỹ tích trung điểm I của MN khi cát tuyến MAN quay quanh A.
Bài 54. Cho ABC đều nội tiếp (O). Trên cung nhỏ
ằ
AC
lấy một điểm D. Trên dây BD lấy điểm M
sao cho DM = DC.
a) MCD là tam giác gì ?
b) Tìm quỹ tích điểm M khi D di động trên cung nhỏ

ằ
AC
.
Bài 55. Cho cung một phần t đờng tròn với hai bán kính OA, OB vuông góc với nhau. Trên cung
này lấy một điểm C tùy ý không trùng với A và B. Vẽ CH OA. Gọi I là tâm đờng tròn nội
tiếp HOC.
a) Tính số đo góc OIC.
b) Chứng minh AIO = CIO.
c) Tìm quỹ tích I khi C di động trên cung
ằ
AB
.
Bài 56. Cho đờng tròn cố định (O) và điểm A cố định trên đó. Một góc nhọn xAy = x không đổi
quay quanh A, cạnh Ax cắt (O) tại B, cạnh Ay cắt (O) tại C. Gọi H là trực tâm ABC.
a) Tính số đo góc nhọn mà BH và CH tạo ra.
b) Tìm quỹ tích H.
Bài 57. Cho đờng tròn (O) và P cố định ở ngoài (O). Qua P vẽ cát tuyến thay đổi cắt (O) tại A, B.
Gọi I là trung điểm của AB. Trên đờng thẳng OI lấy hai điểm M và M sao cho IM = IP.
Tìm quỹ tích M khi cát tuyến PAB thay đổi.
Bài 58. Cho đờng tròn (O) ngoại tiếp ABC với B, C cố định. Gọi B, C lần lợt là đối xứng của B
qua AC và của C qua AB. BC cắt CB tại M. Tiếp tuyến của (O) tại B và C cắt nhau tại P.
Chứng tỏ rằng khi A di chuyển trên (O) thì M di chuyển trên đờng tròn ngoại tiếp BPC.
Bài 59. Cho hai đờng tròn (O) và (O) cắt nhau tại A, B. Một đờng thẳng qua B cắt (O) tại C và
(O) tại D. Tiếp tuyến của (O) tại C và tiếp tuyến của (O) tại D cắt nhau ở I. Chứng minh
rằng đờng tròn ngoại tiếp ICD luôn đI qua một điểm cố định khi cát tuyến CBD thay đổi.
Bài 60. Dựng hình vuông ABCD biết đỉnh A và hai điểm : M thuộc cạnh BC, N thuộc cạnh CD.
VI tứ giác nội tiếp.
Bài 61. Cho ba đờng tròn cùng đi qua điểm P. Gọi các giao điểm còn lại của chúng là A, B, C. Từ
một điểm D trên đờng tròn (PBC) kẻ các tia DB, DC cắt các đờng tròn (PAB) và (PAC) tại M
và N. CMR: M, A, N thẳng hàng.

Bài 62. Cho nửa đờng tròn (O) đờng kính AB và tiếp tuyến Bx của nửa đờng tròn. Trên tia Bx lấy
hai điểm C, D ( C nằm giữa B và D). Các tia AC, AD lần lợt cắt đờng tròn tại E và F. Hai dây
AE , BF cắt nhau tại M. Hai tia AF, BE cắt nhau tại N. Chứng minh rằng :
a) Tứ giác FNEM nội tiếp.
b) Tứ giác CDFE nội tiếp.
Bài 63. Cho ABC. Hai đờng cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua
trung điểm M của BC.
a) Chứng minh rằng tứ giác ABDC nội tiếp. Tìm tâm O của đờng tròn đó.
b) Đờng thẳng DH cắt (O) tại điểm thứ hai là I. Chứng minh rằng A, I, F, H, E cùng nằm
trên một đờng tròn.
Bài 64. Cho hai đờng tròn (O) và (O) cắt nhau tại A và B. Tia OA cắt (O) tại C. Tia OA cắt (O)
tại D. CMR: O, O, B, C, D cùng nằm trên một đờng tròn.
Bài 65. Cho hình vuông ABCD. Trên cạnh AB lấy một điểm M. Đờng thẳng qua C vuông góc với
CM cắt các tia AB, AD lần lợt tại E và F. Tia CM cắt đờng thẳng AD tại N. Chứng minh rằng
:
a) Các tứ giác AMCF và ANEC nội tiếp.
b) CM + CN = EF.
Bài 66.Cho tứ giác ABCD nội tiếp nửa đờng tròn đờng kính AD. Hai đờng chéo AC và BD cắt
nhau tại E. Vẽ EF vuông góc với AD. Gọi M là trung điểm của DE. Chứng minh rằng :
a) Các tứ giác ABEF, DCEF nội tiếp.
b) Tia CA là phân giác của góc BCF.
c)
*
Tứ giác BCMF nội tiếp.
Bài 67. Cho hai đờng tròn (O) và (O) cắt nhau tại M và P. Kẻ dây MA của (O) tiếp xúc với (O)
tại M. Kẻ dây MB của (O) tiếp xúc với (O) ở M. Trên tia MP lấy H sao cho PH=PM. CMR:
Tứ giác MAHB nội tiếp.
Bài 68. Cho hình thang ABCD nội tiếp trong (O). Các đờng chéo AC, BD cắt nhau tại E, các cạnh
AD, BC kéo dài cắt nhau tại F. CMR:
a) A, D, O, E cùng nằm trên một đờng tròn.

b) Tứ giác AOCF nội tiếp.
Bài 69. Cho ABC vuông tại C. Trên AB dựng hình vuông ABMN có tâm I. Chứng minh rằng CI
là phân giác của góc tạo bởi AC và BC.
Bài 70. Hai cạnh AB và DC của tứ giác ABCD kéo dài cắt nhau tại E, AD và BC kéo dài cắt nhau
tại F. Chứng minh các đờng tròn ngoại tiếp các tam giác AED, EBC, ABF và CDF cùng đi
qua một điểm.
Bài 71. Cho góc vuông xOy và ABC vuông ở A và góc B bằng 30
0
, BC=a. Tam giác ABC di
chuyển trong góc vuông xOy sao cho đỉnh B chạy trên Ox, đỉnh C trên Oy, A và O khác phía
đối với BC. Tìm quỹ tích điểm A.
Bài 72. Hai đờng tròn (O) và (O) cắt nhau tại A và B. Một cát tuyến qua A cắt các đờng tròn này
tại M, N. Các tiếp tuyến tại A của (O), (O) theo thứ tự cắt BN và BM ở P và Q. Chứng minh
PQ // MN.
Bài 73. Cho ABC đều. Một nửa đờng tròn có tâm O trên cạnh AB, tiếp xúc với AC, BC tại K và
I. Kẻ một tiếp tuyến với nửa đờng tròn cắt các cạnh BC và AC tại M và N. Đoạn thẳng KI cắt
OM và ON tại P, Q. CMR: MN=2PQ.
Bài 74. Cho đờng tròn (O) có đờng kính AB cố định. Một điểm C chạy trên đờng tròn. Kẻ CD
vuông góc với AB. Trên OC lấy M sao cho OM = CD. Tìm tập hợp điểm M khi C di chuyển
trên (O).
Bài 75. Cho đờng tròn (O) có đờng kính AB cố định. (d) là tiếp tuyến của (O) tại A. M là điểm di
động trên (d); MB cắt (O) tại C. N là trung điểm của cung
ằ
BC
. ON cắt BC tại P.
a) Chứng minh tứ giác MAOP nội tiếp.
b) Tìm tập hợp điểm P khi m di động trên (d).
Bài 76. Cho ABC vuông tại A. Trên đoạn AB lấy D. Đờng tròn đờng kính BD cắt BC tại E và CD
tại F. Chứng minh rằng :
a) Tứ giác ACBF nội tiếp.

b) D là tâm đờng tròn nội tiếp AEF.
c) B là tâm đờng tròn bàng tiếp của AEF.
Bài 77. Cho hai đờng tròn (O) và (O) cắt nhau tại B và C. A là điểm trên (O). AB cắt (O) tại D,
AC cắt (O) tại E. AO cắt DE tại H. I là trung điểm của BC.
a) Chứng minh tứ giác OIDH nội tiếp. Suy ra AH DE.
b) (d) là tiếp tuyến của (O) tại A. Chứng minh (d) // DE.
Bài 78. Cho đờng tròn (O;R) và điểm A ở ngoài (O). Qua A vẽ tiếp tuyến AB của (O), B là tiếp
điểm; vẽ cát tuyến ACD thay đổi cắt (O) tại C và D. Gọi H là hình chiếu của B lên AO.
a) Chứng minh AB
2
= AC.AD
b) Gọi I là giao điểm của BH và CD, J là trung điểm của CD. Chứng minh : AI.AJ =
AH.AO
Bài 79. Cho hình thang cân ABCD (AB // CD) có đờng trung bình bằng một cạnh bên. Chứng minh
ABCD có đờng tròn nội tiếp.
Bài 80.Cho đờng tròn (O) và một tiếp tuyến tại A. Trên tiếp tuyến lấy một điểm C (khác A). Gọi B
là trung điểm của AC. Kẻ cát tuyến BEF (E và F thuộc (O) ). Các tia CE và CF cắt (O) tại M
và N. Chứng minh MN // AC.
VII độ dài diện tích cung tròn đ ờng tròn.
Bài 81. Cho ngũ giác đều ABCDE, AD và BE cắt nhau tại O. Chứng minh: DO
2
= AO.AD
Bài 82. Cho đờng tròn (O) đờng kính AB. Lấy điểm M trên AB. Vẽ dây CD AB tại M. Giả sử
AM=1cm, CD=
2 3
cm. Tính :
a) Độ dài đờng tròn.
b) Độ dài cung
ẳ
CAD

.
Bài 83. Một tam giác đều và một hình vuông có cùng chu vi là 72 cm. Hỏi độ dài đờng tròn ngoại
tiếp hình nào lớn hơn ? Lớn hơn bao nhiêu ?
Bài 84. Trên hình dới có nửa đờng tròn (O) đờng kính AB = 2R. C là điểm chính giữa của nửa đ-
ờng tròn. Cung
ằ
AD
có tâm B bán kinh 2R. Cung
ằ
BE
có tâm C bán kính CD.
a) Chứng minh
ằ
AC
=
ằ
AD
.
b) Tính độ dài của đờng cong ADEB do ba cung
ằ
AD
,
ằ
BE
,
ằ
DE
chắp nối thành.
A
O

B
C
E
D
Bài 85. Cho ABC vuông tại A, góc C là 30
0
và AB = 4cm. Vẽ đờng cao AH. Gọi M, N theo thứ
tự là trung điểm của AB và AC.
a) Chứng minh rằng tứ giác AMHN nội tiếp.
b) Tính độ dài đờng tròn ngoại tiếp tứ giác AMHN.
Bài 86. Tính diện tích hình vành khăn tạo thành bởi đờng tròn nội tiếp và ngoại tiếp tam giác đều
cạnh 6 cm.
Bài 87. Cho nửa đờng tròn đờng kính BC=10 cm và dây BA = 8cm. Vẽ ra phía ngoài ABC các
nửa đờng tròn đờng kính AB và AC.
a) Tính diện tích ABC.
b) Tính tổng diện tích hai hình viên phân.
c) Tính tổng diện tích hai hình trăng khuyết.
Bài 88. Cho ABC nội tiếp đờng tròn (O). Biết BC=2cm, góc

A
=45
0
.
a) Tính diện tích hình tròn (O).
b) Tính diện tích hình viên phân BC (ứng với cung nhỏ
ằ
BC
).
c) Xác định vị trí của A để diện tích ABC lớn nhất. Tính diện tích đó.
Bài 89. Cho đờng tròn (O) và một dây cung AB=6cm. Gọi D là trung điểm của dây AB. Tia DO cắt

đờng tròn tại C. Biết CD=9cm. Hãy tính độ dài của đờng tròn (O).
Bài 90.Cho ABC vuông ở A và đờng cao AH. Dựng đờng tròn tâm O đờng kính AB. Biết BH =
2cm và HC = 6cm. Tính:
a) Diện tích hình tròn (O).
b) Tổng diện tích hai hình viên phân AH và BH (ứng với các cung nhỏ).
c) Diện tích hình quạt tròn AOH (ứng với cung nhỏ
ẳ
AH
).
Bài 91. Cho AHB có

H
=90
0
,

A
=30
0
vaf BH=4cm. Tia phân giác của góc B cắt AH tại O. Dựng
đờng tròn (O;OH) và đờng tròn (O;OA) .
a) Chứng minh rằng (O;OH) tiếp xúc với AB.
b) Tính diện tích hình vành khăn giữa hai đờng tròn trên.
Bµi 92. Cho mét phÇn t ®êng trßn cã hai b¸n kÝnh vu«ng gãc lµ OA vµ OB b»ng R. C lµ mét ®iĨm
trªn ®ã. VÏ trong ®ã hai nưa ®êng trßn cã ®êng kÝnh OA vµ OB. Gäi giao ®iĨm cđa hai nưa
®êng trßn ®ã lµ D. Chøng minh r»ng:
a) A, B, D th¼ng hµng.
b) Hai h×nh ACBDA vµ OEDFO cã cïng diƯn tÝch.
c) DiƯn tÝch c¸c h×nh OFDAO vµ OEDBO b»ng 1/4 diƯn tÝch h×nh vu«ng c¹nh OA.
Bµi 93. Cho ®êng trßn (O) ®êng kÝnh AB=2R. Trªn tia ®èi cđa tia AB ta lÊy mét ®iĨm P sao cho

PA=R. VÏ d©y BD=R. §o¹n th¼ng PD c¾t ®êng trßn (O) t¹i C.
a) Chøng minh PC.PD = AD
2
.
b) Gäi cung nhá c¨ng d©y BD lµ cung
¼
BmD
. TÝnh diƯn tÝch cđa h×nh AbmD.
Bµi 94. Cho ®êng trßn (O;3cm) tiÕp xóc ngoµi t¹i A víi ®êng trßn (O’;1cm). KỴ tiÕp tun chung
ngoµi BC cđa chóng (B, C lµ c¸c tiÕp ®iĨm vµ B n»m trªn (O) ).
a) X¸c ®Þnh t©m I cđa ®êng trßn ngo¹i tiÕp ∆ ABC vµ tÝnh diƯn tÝch cđa h×nh trßn (I).
b) TÝnh ®é dµi c¸c cung AB vµ AC n»m trong ®êng trßn (I) cđa c¸c ®êng trßn (O) vµ (O’).
c) TÝnh diƯn tÝch h×nh tam gi¸c cong giíi h¹n bëi hai ®êng trßn (O), (O’) vµ tiÕp tun
chung BC.
Bµi 95. Cho ∆ ABC ®Ịu cã c¹nh b»ng 4 cm. VÏ nưa h×nh trßn ®êng kÝnh BC thc nưa mỈt ph¼ng
chøa A bê lµ BC. H·y tÝnh diƯn tÝch phÇn h×nh trßn ë ngoµi tam gi¸c.
Bµi 96. §êng trßn (P) néi tiÕp trong mét h×nh qu¹t trßn øng víi gãc ë t©m O b»ng 60
0
. BiÕt r»ng
b¸n kÝnh ®êng trßn (P) lµ R, h·y tÝnh b¸n kÝnh ®êng trßn (O).
Bµi 97. Trªn ®o¹n th¼ng AB lÊy mét ®iĨm C. VÏ trong cïng mét mỈt ph¼ng bê AB c¸c nưa ®êng
trßn ®êng kÝnh AB, AC vµ BC. KỴ CD vu«ng gãc víi AB (D thc ®êng trßn ®êng kÝnh AB).
Chøng minh r»ng diƯn tÝch phÇn mỈt ph¼ng giíi h¹n bëi ba nưa ®êng trßn b»ng diƯn tÝch
h×nh trßn ®êng kÝnh CD.
Bµi 98. Trong ®êng trßn (O;R) ta vÏ hai ®êng trßn (O
1
;R/2) vµ (O
2
;R/2) tiÕp xóc nhau t¹i O. VÏ
tiÕp hai ®êng trßn (O

3
) vµ (O
4
) mçi ®êng trßn ®Ịu tiÕp xóc víi hai ®êng trßn (O
1
) vµ (O
2
) vµ
tiÕp xóc víi (O).
a) TÝnh b¸n kÝnh cđa (O
3
) vµ (O
4
) theo R.
b) TÝnh tØ sè tỉng diƯn tÝch bèn h×nh trßn nhá vµ diƯn tÝch (O).
BÀI TẬP ÔN CHƯƠNG III HÌNH HỌC 9
A- PHẦN TRẮC NGHIỆM : Khoanh tròn câu trả lời đúng nhất.
Câu 1: Kim giờ và kim phút của một đồng hồ tạo thành một góc ở tâm bằng 90
0
vào lúc:
a) 5 giờ b) 9 giờ c) 6 giờ d) 12 giờ
Câu 2: Cho đường tròn (O) , Góc ở tâm AOB = 120
0
, góc ở tâm AOC = 30
0
. Số đo cung nhỏ
BC là:
a) 90
0
b) 150

0
c) 90
0
hoặc 150
0
d) Kết quả
khác.
Câu 3: Đối với hai cung nhỏ trong một đường tròn, phát biểu nào sau đây sai ?
a) Cung lớn hơn căng dây lớn hơn b) Cung nhỏ hơn căng dây nhỏ hơn
c) Cung bằng nhau căng dây bằng nhau d) Cung nhỏ hơn căng dây lớn hơn
Câu 4:Một góc nội tiếp có số đo bằng 30
0
thì số đo cung bò chắn bằng:
a) 60
0
b) 30
0
c) 15
0

d) Một số đo khác
Câu 5: Số đo của một góc nội tiếp không quá 90
0
thì :
a) Bằng nửa số đo cung bò chắn b) Bằng số đo cung bò chắn
c) Bằng nửa số đo góc ở tâm cùng chắn 1 cung d) Cả a, c đúng.
Câu 6: Gọi α là số đo của góc nội tiếp chắn nửa đường tròn, ta có:
a) α < 90
0
b) α = 90

0
c) α > 90
0
d) α = 180
0
Câu 7: Một tứ giác nội tiếp thì :
a) Có hai đường chéo vuông góc với nhau. b) Có tổng các góc đối bằng 180
0
c) Có bốn đỉnh nằm trên một đường tròn d) Cả b, c đúng
Câu 8: Cho tứ giác ABCD nội tiếp đường tròn có Â = 98
0
, khi đó góc C có số đo bằng:
a) 98
0
b) 89
0
c) 92
0
d) 82
0
Câu 9: Trong các hình sau đây hình nào nội tiếp được trong một đường tròn:
a) Hình thang cân b) Hình bình hành c) Hình thoi d) Cả a, c đều đúng
Câu 10: Độ dài đường tròn có bán kính 3cm là:
a) 3 (cm) b) 9 (cm) c) 6 (cm) d) Tất cả đều sai
Câu 11: Công thức tính diện tích hình tròn có dạng tổng quát là:
a)
2
S .R= π
b)
S 2 R= π

c)
2
S d= π
d) Cả a, c đúng
Câu 12: Độ dài cung 60
0
của một đường tròn có bán kính 6cm là:
a)  (cm) b) 2 (cm) c) 3 (cm) d) Độ dài khác.
Câu 13: Nếu bán kính hình tròn tăng 3 lần thì diện tích của nó:
a) Tăng 9 lần b) Giảm 9 lần c) Tăng 3 lần d) Tăng 6 lần
Câu 14: Cho AB là một dây cung của đường tròn (O ; R). Phát biểu nào sau đây sai ?
a) Nếu AB = R thì góc ở tâm
·
AOB
= 60
0
b) Nếu AB = R
2
thì góc ở tâm
·
AOB
= 90
0
c) Nếu AB = R
3
thì góc ở tâm
·
AOB
= 120
0

d) Cả a, b, c sai
Câu 15: Cho tam giác ABC (vuông cân tại A) nội tiếp trong đường tròn tâm O, kết luận nào
sai ?
a) sđ
»
AB
= 90
0
b) sđ
»
BC
= 180
0
c) sđ
»
BC
= sđ
»
BA
+sđ
»
AC
d) sđ
»
AC
=45
0
Câu 16: Để phát biểu “Số đo của góc nội tiếp ……… cung bò chắn tương ứng” là phát biểu
đúng, phải điền vào chỗ trống (…) cụm từ:
a) bằng nửa b) bằng c) bằng nửa số đo của d) bằng số đo của.

B- PHẦN TỰ LUẬN:
Bài 1 Cho hình vẽ bên, biết Ax là tiếp tuyến của đường tròn (O) và
·
0
AMB = 46
. Tính số đo các góc ANB, AOB, xAB.
Bài 2 Cho tứ giác ABCD nội tiếp đường tròn (O). Biết
µ
B
= 65
0
;
µ
C
= 102
0
. Tính số đo các góc A và D.
0
46
x
O
M
N
B
A
Bài 3 Cho hình vẽ bên, biết OM = 3cm ;
·
MON
= 120
0

. Tính ( làm
tròn đến chữ số thập phân thứ hai )
a) Độ dài đường tròn (O).
b) Diện tích hình quạt OMmN. ( phần gạch sọc )
c) Số đo góc MAN.
Bài 4 Cho đường tròn (O) đường kính AB. Trên đường thẳng AB ta lấy một điểm M sao cho
điểm B nằm giữa hai điểm A và M. Kẻ hai tiếp tuyến MN và MP với đường tròn (N, P là hai
tiếp điểm ).
a) Chứng minh tứ giác MNOP nội tiếp.
b) Gọi H là giao điểm của NP và AB. Chứng minh NP
⊥
AB.
c) Chứng minh OH . MH = AH . BH

Bài 5 Cho nửa đường tròn tâm O đường kính AB = 2R. Trên nửa mặt phẳng bờ AB chứa nửa
đường tròn, lấy điểm S sao cho SA và SB lần lượt cắt nửa đường tròn tại M và N. Gọi H là
giao điểm của AN và BM. Chứng minh:
a) Tứ giác SMHN nội tiếp được trong một đường tròn.
b) SH vuông góc với AB.
c) Biết
·
NAB
= 30
0
. Tính theo R diện tích hình quạt tròn NOB.
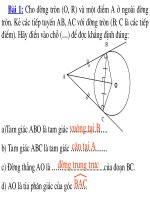
PHẦN ĐỀ BÀI ÔN TẬP CHƯƠNG ĐƯỜNG TRÒN
1. Cho đường tròn (O ; R) cố đònh và đường thẳng d cố đònh nằm bên ngoài đường tròn.Gọi H
là chân đường vuông góc kẽ từ O đến d. Gọi M là điểm di động trên d; MA và MB là hai tiếp
tuyến của (O ; R) ( A và B là các tiếp điểm ) .
a) CMR: A ; B ; O ; H ; M cùng thuộc một đường tròn.

b) Dây AB của (O ; R) lần lượt cắt các đoạn thẳng OH và OM tại I và K .
CMR: OI . OH = OK . OM = R
2
.
c) CMR: Khi M thay đổi trên d thì dây AB luôn đi qua một điểm cố đònh. ( G/ý: OI = ?)
2. Cho đường tròn (O) đường kính AB ; M là điểm thuộc (O) ( M khác A và B) . Gọi C là điểm
đối xứng với A qua M . Đường thẳng qua A và song song với MB cắt (O) lần nữa tại D. Gọi E
là điểm đối xứng với A qua D . CMR:
a) Góc
·
MBD
vuông và C , B , E thẳng hàng.
b) Xác đònh vò trí M thuộc (O) đểû CE là tiếp tuyến của (O) .
3. Cho đường tròn (O) và đường tròn (O') tiếp xúc ngoài tại A. Một cát tuyến qua A lần lượt
cắt (O) và (O') tại các điểm khác là B và C .
a) CMR: OB // O'C .
b) Vẽ đường kính CD của (O') ; gọi E là trung điểm của BD. Tính số đo góc
·
OEO'
( G/ý: Gọi I
là trung điểm OO' ) .
4. Cho △ ABC vuông tại A ( AB < AC ) , đường cao AH. Gọi E là điểm đối xứng với B qua H.
Đường tròn (O) đường kính CE cắt cạnh AC tại điểm khác là K. CMR:
a) HA = HK ( G/ý: Gọi M là trung điểm AK) .
b) HK là tiếp tuyến của (O) .
5. Trên nửa đường tròn (O) đường kính AB lấy điểm M ( M khác A và B). Gọi d là tiếp tuyến
của (O) tại M ; D và C lần lượt là hình chiếu của A và B lên d.
a) CMR: AB = BC + AD. ( G/ý = 2.OM)
b) Kẽ MH ⊥ AB tại H. Tính số đo góc
·

DHC
.
c) Xác đònh vò trí M thuộc nửa (O) để S
ABCD
lớn nhất.
6. Trên nửa (O) đường kính AB lấy điểm C ( C khác A và B) . Gọi d là tiếp tuyến tại C của
nửa (O) . Qua A và B kẽ hai đường thẳng song song với nhau ( không nhất thiết vuông góc với
AB ) lần lượt cắt d tại D và E . Gọi M là trung điểm DE ; H là hình chiếu của M lên AB .
CMR:
a) S
AOM
= S
DOM
từ đó suy ra MH = MD .
b) AB là tiếp tuyến của đường tròn đường kính DE .
7. Cho (O ; R) và (O'; R) cắt nhau tại A và H . Vẽ (O"; R) đi qua H và lần lượt cắt (O;
R) ; (O'; R) tại các điểm khác là B và C . CMR:
a) ABO''O' là hình bình hành.
b) △ABC = △O"O'O.
c) H là trực tâm △ABC.
8. Cho A nằm bên ngoài (O) ; vẽ ( A ; AO) . Gọi CD là một tiếp tuyến chung ngoài của hai
đường tròn ( C thuộc (O) , D thuộc (A) ) . Đoạn nối tâm OA cắt (O) tại H. Gọi M là trung điểm
OD ; AM cắt DH tại K . CMR:
a) DH là tiếp tuyến của (O). ( G/ý:
△
=
△
(c.g.c) )
b) Tính số đo góc
·

KOC
.
9. Cho (O; 3cm) và (O'; 1cm) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung ngoài (B thuộc
(O) ; C thuộc (O') ) .
a) Tính độ dài đoạn thẳng BC .
b) Gọi BD là đường kính của (O). CMR: D , A , C thẳng hàng ( G/ý:
·
·
'AOD AO C=
).
c) Tính độ dài các đoạn thẳng BA ; AC ( G/ý: 1 / h
2
= ? ).
10. Cho (O) và (O') tiếp xúc ngoài tại A . Đường nối tâm OO' lần lượt cắt (O) và (O') tại các
điểm khác là B và C . Gọi DE là một tiếp tuyến chung ngoài ( D thuộc (O) ; E thuộc (O') ) .
Các đường thẳng BD và CE cắt nhau tại K ; gọi M là trung điểm BC. CMR:
a) DE = AK ( G/ý:
·
·
0
DOA+EO'A 180=
; ADKE là hình chữ nhật )
b) AK là tiếp tuyến chung của (O) và (O') .
c) KM ⊥ DE .
11. Cho nửa (O; R) đường kính AB . Trên nửa đường tròn lấy điểm C sao cho góc
·
AOC
nhọn.
Tiếp tuyến tại C cắt tia đối của tia AB ở D . Tia phân giác góc
·

CBD
cắt nửa (O) tại E và F.
Gọi M là trung điểm dây EF; tia OM cắt tia DC tại K.
a) Tứ giác OEKF là hình gì ? .
b) Tính theo R khoảng cách từ K đến đường thẳng AB .
12. Cho nửa (O) đường kính AB . Gọi H là điểm tùy ý nằm giữa O và A . Đường thẳng vuông
góc với AB tại H cắt nửa (O) tại C . Gọi M là trung điểm CH; K là hình chiếu của M lên OC .
Tia MK cắt nửa (O) tại D. CMR:
a) CH
2
= 2. CK . CO
b
*
) AB tiếp xúc với đường tròn ( C; CD). ( G/ý: Dùng HT Lượng thứ nhất )
13. Cho đường tròn (O) nội tiếp △ABC và tiếp xúc các cạnh AB; BC; CA lần lượt tại D; F; E .
Gọi I là hình chiếu của F lên đoạn DE . CMR:
a) AB + AC - BC = 2.AD
b*)
· ·
BIF=CIF
. ( G/ý: Kẽ các đường vuông góc thích hợp) .
c) Giả sử
·
0
BOC 135=
; khi đó tứ giác ADOE là hình gì ? .
14. Cho nửa (O) đường kính AB ; vẽ đường tròn (O') tiếp xúc trong với nửa (O) tại C và tiếp
xúc với bán kính OA tại I . Các dây CA và CB của nửa (O) lần lượt cắt (O') tại các điểm khác
là N và M . Tiếp tuyến tại M của (O') cắt AB tại D và cắt nửa (O) tại P. CMR:
a) M; O'; N thẳng hàng .

b) MN // AB .
c) BM . BC = BD . BA
d*) BI = BP. ( G/ý: Dùng H.T.Lượng thứ nhất)


C¸C BµI TËP H×NH HäC TỉNG HỵP
C©u 1 : ( 3 ®iĨm ). Cho tam gi¸c vu«ng ABC (
µ
C
= 90
0
) néi tiÕp trong ®êng trßn t©m O .
Trªn cung nhá AC ta lÊy mét ®iĨm M bÊt kú ( M kh¸c A vµ C ) . VÏ ®êng trßn t©m A b¸n kÝnh
AC , ®êng trßn nµy c¾t ®êng trßn (O) t¹i ®iĨm D ( D kh¸c C ) . §o¹n th¼ng BM c¾t ®êng trßn
t©m A ë ®iĨm N .
a) Chøng minh MB lµ tia ph©n gi¸c cđa gãc
·
CMD
.
b) Chøng minh BC lµ tiÕp tun cđa ®êng trßn t©m A nãi trªn .
c) So s¸nh gãc CNM víi gãc MDN .
d) Cho biÕt MC = a , MD = b . H·y tÝnh ®o¹n th¼ng MN theo a vµ b .
C©u 2 : ( 3 ®iĨm )
Cho ABCD lµ mét tø gi¸c néi tiÕp . P lµ giao ®iĨm cđa hai ®êng chÐo AC vµ BD .
a) Chøng minh h×nh chiÕu vu«ng gãc cđa P lªn 4 c¹nh cđa tø gi¸c lµ 4 ®Ønh cđa mét tø
gi¸c cã ®êng trßn néi tiÕp .
b) M lµ mét ®iĨm trong tø gi¸c sao cho ABMD lµ h×nh b×nh hµnh . Chøng minh r»ng nÕu
gãc CBM = gãc CDM th× gãc ACD = gãc BCM .
c) T×m ®iỊu kiƯn cđa tø gi¸c ABCD ®Ĩ :
) (

2
1
BCADCDABS
ABCD
+=
C©u 3 ( 3 ®iĨm ). Cho tam gi¸c vu«ng ABC ( gãc A = 90
0
) néi tiÕp ®êng trßn t©m O , kỴ
®êng kÝnh AD .
1) Chứng minh tứ giác ABCD là hình chữ nhật .
2) Gọi M , N thứ tự là hình chiếu vuông góc của B , C trên AD , AH là đờng cao của tam
giác ( H trên cạnh BC ) . Chứng minh HM vuông góc với AC .
3) Xác định tâm đờng tròn ngoại tiếp tam giác MHN .
4) Gọi bán kính đờng tròn ngoại tiếp và đờng tròn nội tiếp tam giác ABC là R và r .
Chứng minh
ACABrR .+
Câu 4 ( 4 điểm ). Cho tam giác ABC nội tiếp đờng tròn tâm O , đờng phân giác trong của
góc A cắt cạnh BC tại D và cắt đờng tròn ngoại tiếp tại I .
a) Chứng minh rằng OI vuông góc với BC .
b) Chứng minh BI
2
= AI.DI .
c) Gọi H là hình chiếu vuông góc của A trên BC .
Chứng minh góc BAH = góc CAO .
d) Chứng minh góc HAO =
à à
B C
Câu 5 ( 3 điểm ). Cho tam giác ABC , M là trung điểm của BC . Giả sử góc
ã
ã

BAM BCA=
.
a) Chứng minh rằng tam giác ABM đồng dạng với tam giác CBA .
b) Chứng minh minh : BC
2
= 2 AB
2
. So sánh BC và đờng chéo hình vuông cạnh là AB .
c) Chứng tỏ BA là tiếp tuyến của đờng tròn ngoại tiếp tam giác AMC .
d) Đờng thẳng qua C và song song với MA, cắt đờng thẳng AB ở D . Chứng tỏ đờng tròn
ngoại tiếp tam giác ACD tiếp xúc với BC .
Câu 6 ( 3 điểm ). Cho hình bình hành ABCD có đỉnh D nằm trên đờng tròn đờng kính AB . Hạ
BN và DM cùng vuông góc với đờng chéo AC .
Chứng minh :
a) Tứ giác CBMD nội tiếp .
b) Khi điểm D di động trên trên đờng tròn thì
ã
ã
BMD BCD+
không đổi .
c) DB . DC = DN . AC
Câu 7 ( 4 điểm ).
Cho tứ giác ABCD nội tiếp trong đờng tròn tâm O . Gọi I là giao điểm của hai đờng chéo
AC và BD , còn M là trung điểm của cạnh CD . Nối MI kéo dài cắt cạnh AB ở N . Từ B kẻ đờng
thẳng song song với MN , đờng thẳng đó cắt các đờng thẳng AC ở E . Qua E kẻ đờng thẳng song
song với CD , đờng thẳng này cắt đờng thẳng BD ở F .
a) Chứng minh tứ giác ABEF nội tiếp .
b) Chứng minh I là trung điểm của đoạn thẳng BF và AI . IE = IB
2
.

c) Chứng minh
2
2
NA IA
=
NB IB
Câu 8 ( 3 điểm ). Cho đờng tròn tâm O . A là một điểm ở ngoài đờng tròn , từ A kẻ tiếp tuyến
AM , AN với đờng tròn , cát tuyến từ A cắt đờng tròn tại B và C ( B nằm giữa A và C ) . Gọi I là
trung điểm của BC .
1) Chứng minh rằng 5 điểm A , M , I , O , N nằm trên một đờng tròn .
2. Một đờng thẳng qua B song song với AM cắt MN và MC lần lợt tại E và F . Chứng minh
tứ giác BENI là tứ giác nội tiếp và E là trung điểm của EF
Câu 9 (3điểm )
Cho tam giác nhọn ABC và đờng kính BON . Gọi H là trực tâm của tam giác ABC , Đờng
thẳng BH cắt đờng tròn ngoại tiếp tam giác ABC tại M .
1) Chứng minh tứ giác AMCN là hình thanng cân .
2) Gọi I là trung điểm của AC . Chứng minh H , I , N thẳng hàng .
3) Chứng minh rằng BH = 2 OI và tam giác CHM cân .
Câu 10 ( 3 điểm )
Cho hình thoi ABCD có góc A = 60
0
. M là một điểm trên cạnh BC , đờng thẳng AM cắt
cạnh DC kéo dài tại N .Chứng minh : AD
2
= BM.DN .
a) Đờng thẳng DM cắt BN tại E . Chứng minh tứ giác BECD nội tiếp .
b) Khi hình thoi ABCD cố định . Chứng minh điểm E nằm trên một cung tròn cố định khi
m chạy trên BC .
Câu 11 ( 3 điểm )
Cho hình vuông ABCD cố định , có độ dài cạnh là a .E là điểm đi chuyển trên đoạn CD ( E

khác D ) , đờng thẳng AE cắt đờng thẳng BC tại F , đờng thẳng vuông góc với AE tại A cắt đờng
thẳng CD tại K .
1) Chứng minh tam giác ABF = tam giác ADK từ đó suy ra tam giác AFK vuông cân .
2) Gọi I là trung điểm của FK , Chứng minh I là tâm đờng tròn đi qua A , C, F , K .
3) Tính số đo góc AIF , suy ra 4 điểm A , B , F , I cùng nằm trên một đờng tròn .
Câu 12 ( 3 điểm )
Cho hai đờng tròn (O
1
) và (O
2
) có bán kính bằng R cắt nhau tại A và B , qua A vẽ cát tuyến
cắt hai đờng tròn (O
1
) và (O
2
) thứ tự tại E và F , đờng thẳng EC , DF cắt nhau tại P .
1) Chứng minh rằng : BE = BF .
2) Một cát tuyến qua A và vuông góc với AB cắt (O
1
) và (O
2
) lần lợt tại C,D . Chứng minh
tứ giác BEPF , BCPD nội tiếp và BP vuông góc với EF .
Tính diện tích phần giao nhau của hai đờng tròn khi AB = R.
Câu 13 ( 3 điểm )
Cho góc vuông xOy , trên Ox , Oy lần lợt lấy hai điểm A và B sao cho OA = OB . M là
một điểm bất kỳ trên AB .
Dựng đờng tròn tâm O
1
đi qua M và tiếp xúc với Ox tại A , đờng tròn tâm O

2
đi qua M và
tiếp xúc với Oy tại B , (O
1
) cắt (O
2
) tại điểm thứ hai N .
1) Chứng minh tứ giác OANB là tứ giác nội tiếp và ON là phân giác của góc ANB .
2) Chứng minh M nằm trên một cung tròn cố định khi M thay đổi .
3) Xác định vị trí của M để khoảng cách O
1
O
2
là ngắn nhất .
Câu 14 ( 3 điểm )
Cho hình vuông ABCD , trên cạnh BC lấy 1 điểm M . Đờng tròn đờng kính AM cắt đờng
tròn đờng kính BC tại N và cắt cạnh AD tại E .
1) Chứng minh E, N , C thẳng hàng .
2) Gọi F là giao điểm của BN và DC . Chứng minh
CDEBCF =
3) Chứng minh rằng MF vuông góc với AC .
MT S BI TON HèNH HC TRONG
CC THI TUYN SINH LP 10
1. Cho tam giỏc u ABC ni tip ng trũn tõm O. K ng kớnh AD.
a. CMR: Tam giỏc ABD l tam giỏc vuụng v DB=DC.
b. Trờn cnh AB ly im E v trờn cnh AC kộo di v phớa C ly im F sao cho BE = CF. CMR:
hai tam giỏc DBE v DCF bng nhau.
c. Ly im N bt k trờn cnh BC. K NI song song vi AC ( I thuc AB) k NJ song song vi AB
(J thuc AC). CMR: tam giỏc JNC l tam giỏc u.
2. Cho tam giỏc ABC cú ba gúc u nhn. k 3 ng cao AD, BE, CF.

a. Gi H l trc tõm ca ca tam giỏc ABC. CMR: t giỏc AFHE ni tip, xỏc nh tõm v bỏn kớnh
ng trũn ngoi tip t giỏc.
b. Gi O l tõm ng trũn ngoi tip tam giỏc ABC, CMR: AO vuụng gúc vi FE.
c. Gi s tam giỏc ABC cõn ti A. CMR: DF l tip tuyn ca ng trũn ngoi tip t giỏc AFHE.
3. Trờn hỡnh vuụng ABCD.
a. Trờn cnh AB ly im E v trờn cnh BC ly im F sao cho AE = BF.
i. CMR: Hai tam giỏc DAE v ABF bng nhau.
ii. AF ct DE ti O. CMR: t giỏc DOFC ni tip.
b. Gi M,N, P, Q l cỏc im ln lt thuc bn cnh ca hỡnh vuụng ABCD. Hi t giỏc NMPQ cú
tớnh cht gỡ chu vi ca nú nh nht?
4. Cho tam giỏc ABC vuụng cõn A.Ly bt k im M thuc cnh AB, qua B k ng thng vuụng gúc
vi CM, ng thng ny ct cỏc ng thng CM, CA ln lt ti D v E. CMR:
a. T giỏc BDAC ni tip.
b. DA l tia phõn giỏc ca gúc EDC.
c. Tam giỏc EDA ng dng vi tam giỏc ECB.
5. Cho tam giỏc ABC cõn C ( gúc C nhn), ni tip trong ng trũn (O). Ly im M bt k trờn cung
nh BC.
a. K ng kớnh COK, CMR: MK l tia phõn giỏc ca gúc AMB.
b. Trờn tia AM ly D sao cho BM = MD ( M nm gia A v D),CMR: MK// BD.
c. Kộo di CM ct BD ti I. CMR:
i. I l trung im BD.
ii. MA + MB

2AC
6. Cho tam giỏc nhn ABC cú AB<AC ni tip ng trũn (O). trờn cung nh AC ly im E sao cho
ã
ã
CBE ACB=
a. CMR: AE//BC.
b. K ng cao AK ( K trờn BC) kộo di AK ct (O) ti D. CMR:

i. Ba im E, O , D thng hng.
ii.
ã
ã
ã
OAD ABC ACB=
c. Gi H l trc tõm tam giỏc ABC, gi s AH = CB. Tớnh BC.
7. Cho tam giỏc ABC khụng cõn cú ba gúc nhn. m l trung im BC, AD l ng cao. Gi E v F l chõn
cỏc ng vuụng gúc k t B v C xung ng kớnh AA ca ng trũn ngoi tip tam giỏc ABC.
a. CMR:
ã
ã
EDC BAE=
b. CMR: DE vuụng gúc AC v MN l ng trung trc ca DE (N - trung im AB)
c. Xỏc nh tõm ng trũn ngoi tip tam giỏc DEF
8. Cho tam giỏc u ABC cnh a vi ng cao AH. M l mt im bt k trờn cnh BC. V
,ME AB MF AC
. Gi O l trung im AM.
a. CMR: 5 im A,E,H,M,F cựng thuc mt ng trũn.
b. T giỏc OEHF l hỡnh gỡ?
c. Tỡm giỏ tr nh nht ca din tớch t giỏc OEHF theo a khi M di ng trờn BC.
9. Cho tam giác ABC có phân giác trong AD và trung tuyến AM. Vẽ đường tròn (O) qua A,D,M cắt AB,AC
ở E và F.
a. CMR: BD.BM = BE.BA; CD.CM = CF. CA
b. So sánh BE và CF.
c. Cho BÂC = 90
0
. CMR:
2 1 1
AD AB AC

= +
10. Cho tam giác ABC nội tiếp đường tròn tâm O với AB<AC. Trên hai cạnh AB, AC lấy hai điểm M, N sao
cho AM = CN.
a. CMR: Với mọi điểm M,N thì đường trung trực của MN luôn qua một điểm I cố định.
b. CMR: 4 điểm A,M,N,I luôn cùng nằm trên một đường tròn.