Cấu trúc dữ liệu và giải thuật (phần 6) potx

Heap sort
Heap sort
 Đánh giá thuật toán:
- Độ phức tạp của giải thuật là O(nlgn)
- Ưu điểm: Nhanh, hiệu quả, và không đòi hỏi về
không gian bộ nhớ
- Nhược điểm: Khi dãy số đã sắp xếp có thứ tự thì
giải thuật này tỏ ra không hiệu quả.
Heap sort
Heap sort
 Bài tập: Cho dãy số sau:
A= [23, 17, 21, 3, 42, 9, 13, 1,2,7,35,4]
Trình bày các bước sắp xếp dãy A theo Heapsort
MERGE SORT
MERGE SORT
Merge sort đ
Merge sort đ
ệ
ệ
qui
qui
 Merge sort đệ qui:
Khi gọi đệ quy, chương trình phân chia ra các
mảng con, rồi tiếp tục sắp xếp đệ quy mảng
con thứ nhất
34
 Ví dụ:
35
42 23 74 11 65 58 94 36 99 87
42 23 74 1165 58 94 36 99 87
74 11

65
42 23
74 11
65
11
65
42 23
11
65
7411
65
11 23
7442
65
T
T
á
á
ch
ch
Tr
Tr
ộ
ộ
n
n
23 42
Merge sort đ
Merge sort đ
ệ

ệ
qui
qui
36
void merge(int a[], int left, int mid, int right)
i:= left; j:= mid+1; k:= left ;
//Kh
ở
i t
ạ
o v
ị
trí con tr
ỏ
while ((i<=mid) &&(j<=right))
{ if (a[i] <= a[j])
{ b[k] = a[i]; i++; }
else { b[k] = a[j]; j++; }
k++;
}
//L
ấ
y ph
ầ
n t
ử
nh
ỏ hơn trong hai
ph
ầ

n t
ử
a[i], a[j] vào dãy b
while (j < right)
{ j++; k++; b[k] = a[j] }
//
đặ
t các ph
ầ
n t
ử
còn l
ạ
i c
ủ
a dãy
a[m+1,r] vào cu
ố
i dãy b
while (i < mid)
{ i++; k++; b[k]= a[i] }
//
đặ
t các ph
ầ
n t
ử
còn l
ạ
i c

ủ
a dãy
a[1,m] vào cu
ố
i dãy b
for (k= left; k<= right; k++) a[k]:= b[k];
//gán b[l,r] tr
ở
l
ạ
i a[l,r]
Merge sort đ
Merge sort đ
ệ
ệ
qui
qui
void mergesort(int a[], int left, int right)
{ int mid=(left+right)/2;
mergesort(a[],left,mid);
mergesort(a[],mid+1,right);
merge(a[],left,mid,right);
}
37
Merge sort tr
Merge sort tr
ự
ự
c ti
c ti

ế
ế
p
p
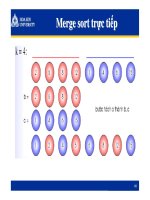
 Merge sort trực tiếp:
- B1: k=1; // Chi
ề
u dài c
ủ
a dãy con trong b
ướ
c hi
ệ
n hành
- B2: Tách dãy a= [a
1
,a
2
, …,a
n
] thành 2 dãy b,c theo
nguyên tắc luân phiên từng nhóm k phần tử
- B3: Trộn từng cặp dãy con gồm k phần tử của dãy
b,c vào a
- B4: k=k*2;
- N
ế
u k <n thì quay l
ạ
i B2.

- Ng
ượ
c l
ạ
i: D
ừ
ng
38
Merge sort tr
Merge sort tr
ự
ự
c ti
c ti
ế
ế
p
p
 Ví dụ:
39
Merge sort tr
Merge sort tr
ự
ự
c ti
c ti
ế
ế
p
p

40