Bài giảng điều khiển quá trình 3 potx

20

Chương 2. Mô hình quá trình
Mô hình hoá là một hình thức biểu diễn các quá trình thực dưới dạng các phương trình toán học,
phương trình đại số hay các mô hình đơn giản hơn nhằm mục đích giúp người kỹ sư nắm bắt tốt hơn về
hệ thống, thực hiện thử nghiệm được các sách lược điều khiển trước khi áp dụng vào mô hình thực.
Điều khiển hiện đại đều dựa trên cơ sở toán học. Mục đích của chương này nhằm giúp người học
nắm rõ về vai trò của của mô hình trong nhiệm vụ phát triển hệ thống về phân tích, thiết kế hệ thống.
Đồng thời nắm được những nguyên tắc cơ bản trong nhiệm vụ mô hình hoá quá trình. Chương này bao
gồm các nội dung sau:
- Giới thiệu những nhiệm vụ của bài toán mô hình hoá.
- Nguyên tắc chung xây dựng những mô hình toán học cho các quá trình công nghệ.
- Bàn luận những vấn đề thế nào là mô hình hoá quá trình công nghệ.
- Các phương pháp mô hình hoá.
- Các phương pháp tiếp cận mô hình hoá
- Từ nhiệm vụ mô hình hoá tạo nên cái nhìn tổng quát về các quá trình công nghệ, rút ngắn thời
gian phân tích và thiết kế hệ thống.

2.1. Giới thiệu chung
2.1.1. Mô hình và mục đích mô hình hoá
Mô hình là một hình thức mô tả khoa học và cô đọng các khía cạnh thiết yếu của một hệ thống
thực. Nghiên cứu thiết kế các hệ thống điều khiển không phải trên mô hình chạy thực, mà trên cơ sở mô
hình là một phương pháp làm việc không thể thiếu của người kỹ sư. Mô hình giúp cho việc phân tích,
kiểm chứng tính đúng đắn của một giải pháp kỹ thuật thuận tiện và ít tốn kém trước khi đưa giải pháp vào
triển khai. Nó cho phép ta thực hiện một số nhiệm vụ phát triển hệ thống mà không cần sự có mặt của hệ
thống thực.
Một mô hình không bao giờ và cũng không cần phản ánh đầy đủ các khía cạnh của hệ thống thực.
Một mô hình tốt cần đơn giản nhưng thâu tóm được các đặc tính thiết yếu cần quan tâm của mô hình thực
trong phạm vi yêu cầu.
Mô hình được hiểu gồm hai phạm trù: Mô hình vật lý và mô hình trừu tượng. Mô hình vật lý là sự

thu nhỏ và đơn giản hoá hệ thống thực. Mô hình vật lý là phương tiện tốt nhất phục vụ công tác đào tạo
và nghiên cứu. Mô hình trừu tượng thường mô tả bằng các ngôn ngữ bậc cao nhằm mô tả một cách logíc
quan hệ của các mặt của một quá trình. Trong kỹ thuật mô hình hoá có bốn dạng mô hình trừu tượng sau:
- Mô hình đồ hoạ: Dùng các ngôn ngữ đồ hoạ như lưu đồ công nghệ, lưu đồ P&ID, sơ đồ khối,
mạng Petri, biểu đồ SFC Mô hình hoá phù hợp cho biểu diễn trực quan một hệ thống về cấu
trúc liên kết và tương tác giữa các thành phần.

21

- Mô hình toán học: Với ngôn ngữ toán học như phương trình vi phân, phương trình đại số,
hàm truyền đạt, phương trình trạng thái. Mô hình toán học phục vụ mục đích nghiên cứu sâu
sắc đặc tính, các mối liên kết và các tương tác.
- Mô hình suy luận: Mô tả bằng thông tin và đặc tính hệ thống thực dưới dạng suy diễn theo tư
duy con người.
- Mô hình máy tính: là các chương trình phần mềm mô tả hệ thống, biểu thị các mặt cần quan
tâm. Các phần mềm được xây dựng trên cơ sở mô hình toán học kết hợp với mô hình suy luận.
Mô hình toán học được xếp vào loại mô hình định lượng, trong khi đó mô hình đồ hoạ biểu diễn
một cách định tính. Mô hình định tính thường quan tâm tới cấu trúc và mối liên quan giữa các thành phần
hệ thống về mặt định tính. Trong khi mô hình định lượng cho phép thực hiện các phép tính để xác định rõ
hơn về mặt định lượng giữa các thành phần bên trong hệ thống và của hệ thống với bên ngoài. Người ta
thường sử dụng mô hình toán học như một khâu then chốt trong nghiên cứu và thiết kế điều khiển. Nó
giúp cho kỹ sư:
- Hiểu rõ về quá trình cần được điều khiển và vận hành.
- Tối ưu hoá thiết kế công nghệ và điều kiện vận hành.
- Thiết kế sách lược và cấu trúc điều khiển.
- Lựa chọn bộ điều khiển và tham số cho bộ điều khiển.
- Phân tích và kiểm chứng kết quả thiết kế.
- Mô phỏng trên máy tính phục vụ đào tạo và vận hành.
Mô hình hoá là vấn đề hết sức cần thiết cho vấn đề lựa chọn mô hình, cấu trúc điều khiển và đơn
giản hoá vận hành.

2.1.2. Nguyên tắc chung của mô hình quá trình
Mô hình hoá là công việc để phát triển hệ thống. Mô hình hoá được xây dựng trên phương pháp
xử lý thông tin có từ hệ thống thực. Cần lưu ý rằng, mô hình nhận được từ hệ thống thực cũng là một hệ
thống đúng nghĩa của nó, một hệ thống lý tưởng đại diện cho hệ thống thực, quá trình thực đang được
quan tâm. Toàn bộ công việc tìm ra tham số của bộ điều khiển cho hệ thống thực trên cơ sở của hệ thống
lý tưởng này.
Các quá trình trong công nghiệp thường rất phức tạp vì vậy mô hình được đưa ra là mô hình xấp
xỉ các đặc tính của quá trình. Mặt khác nếu xây dựng mô hình quá phức tạp thì các đặc tính mô hình chưa
chắc đã chính xác.
Một mô hình quá phức tạp sẽ gây khó khăn cho việc phân tích hệ thống, còn mô hình đơn giản thì
khó có thể biểu diễn hết quan hệ giữa các thành phần trong hệ thống. Vì vậy mô hình tốt nhất là mô hình
đơn giản nhất đáp ứng được các yêu cầu cho hệ thống thực đạt các yêu cầu về tính trung thực theo mục
đích sử dụng nhất định. Việc cân nhắc mô hình hoá theo ba yếu tố sau:
- Yêu cầu mục đích sử dụng của mô hình.
- Công sức và chi phí mô hình hoá

22

- Độ tin cậy thông tin có được về quá trình.

2.1.3. Các phương pháp xây dựng mô hình toán học
Về nguyên tắc, có hai phương pháp xây dựng mô hình toán học cho một quá trình:
- Mô hình hoá bằng lý thuyết: Còn gọi là mô hình hoá vật lý đi từ định luật cơ bản của vật lý
và hoá học kết hợp với các thông số kỹ thuật của công nghệ kết quả nhận được là các phương
trình vi phân (phương trình đạo hàm riêng) và phương trình đại số. Phương pháp này có ưu
điểm là cho ta hiểu biết sâu sắc về các quan hệ bên trong của quá trình, xác định được tương
đối chính xác cấu trúc của mô hình. Tuy nhiên phương pháp này phụ thuộc rất nhiều vào hệ
thống thực, đòi hỏi rất nhiều kinh nghiệm, thời gian, công sức và sự chính xác lại phụ thuộc
vào mức độ chi tiết của mô hình. Bên cạnh đó với các giả thiết không thực tế về điều kiện vận

hành, thành phần nguyên liệu, đặc tính dòng chảy, tốc độ phản ứng… là những yếu tố gây sai
số cho mô hình.
- Mô hình hoá bằng thực nghiệm: Còn gọi là phương pháp hộp đen hay nhận dạng quá trình.
Dựa trên thông tin có được từ quá trình, quan sát tín hiệu vào ra thực nghiệm và phân tích số
liệu thu thập được để xác định cấu trúc và tham số mô hình từ một lớp các mô hình thích hợp.
Phương pháp này cho phép xác định tương đối chính xác các tham số của mô hình và có nhiều
phần mềm rất mạnh hỗ trợ nhận dàng trực tuyến. Tuy nhiên chất lượng phụ thuộc rất nhiều
vào sự chính xác của thiết bị đo.
Phương pháp tốt nhất là phương pháp kết hợp, đó là sự kết hợp của mô hình bằng lý thuyết và
thực nghiệm. Phương pháp này giải quyết tốt quan hệ giữa các thành phần quá trình cũng như các tham số
đối với quá trình. Phân tích lý thuyết giúp ta thiết kế sách lược và lựa chọn bộ điều khiển. Tiếp đó nhận
dạng mô hình cho phép ta một mô hình giúp ta tổng hợp bộ điều khiển, mô phỏng thời gian thực cũng
như đánh giá chất lượng bộ điều khiển trước khi đưa vào sử dụng.

2.2. Tổng quan về quy trình mô hình hoá
Mô hình hoá là một quá trình tương đối phức tạp, vùa mang tính khoa học vừa mang tính mỹ
thuật. Bên cạnh những nguyên tắc và phương pháp cơ bản, để có mô hình tốt cần sáng tạo và có nhiều
kinh nghiệm. Các bước mô hình hoá cần tuân theo trình tự sau:

23


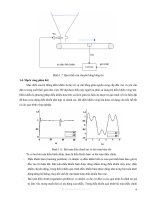
Hình 2. 1. Các bước mô hình hoá quá trình
*Đặt bài toán mô hình hoá
Đây là bước đầu tiên của quá trình mô hình hoá, bao gồm việc tìm hiểu lưu đồ công nghệ, xác
định rõ mục đích sử dụng của mô hình, tóm tắt các thông số công nghệ cũng như giả thiết quan trọng về
tham số và biến quá trình. Trên cơ sở đó ta làm rõ các yêu cầu về mức độ chi tiết và mức độ chính xác
của mô hình. Trong đó việc làm rõ mục đích sử dụng của mô hình là rất quan trọng, nó quyết định mức
độ chính xác và chi tiết của mô hình. Ví dụ để phục vụ sách lược điều khiển ta không cần mô hình quá
phức tạp và chính xác, nhưng để tính toán các tham số bộ điều khiển thì mức độ chính xác của mô hình sẽ

ảnh hưởng rất lớn đến chất lượng điều khiển.
Ví dụ như trong lưu đồ công nghệ chế biến hoá chất hình 2.2 nếu mục đích đặt ra là mô phỏng
thời gian thực thì chỉ riêng phần tháp chưng luyện đã yêu cầu hàng trăm biến trạng thái ứng với nhiệt độ
và mức tại các đĩa trong tháp. Nhưng nếu mục đích đặt ra là để xác định cấu hình điều khiển các thành
phần phù hợp thì một mô hình tuyến tính với hai biến ra (thành phần sản phẩm đỉnh và đáy) và 5 biến vào
(lưu lượng liệu cấp, lưu lượng hồi lưu, lưu lượng hơi nước gia nhiệt, lưu lượng sản phẩm đỉnh và đáy)
cũng có thể là đủ.
Trong việc mô hình hoá các quá trình công nghệ lớn, phức tạp thì cần phải được phân chia thành
các quá trình công nghê con đơn giản hơn. Trên cơ sở đó ta sẽ mô hình cho các quá trình con bằng lý
thuyết hoặc thực nghiệm. Ta thường phân chia một quy trình công nghệ thành các tổ hợp công nghệ, tiếp
theo mỗi tổ hợp công nghệ lại được phân chia thành các quá trình cơ bản, mỗi quá trình công nghệ cũng
có thể được phân chia thành các nguyên công. Việc xây dựng các quá trình toán học có thể được tiến
hành bắt đầu từ mức nguyên công hoặc các quá trình cơ bản, kết hợp cho từng tổ hợp công nghệ và cuối
cùng là cả quy trình công nghệ.

24


Hình 2. 2. Sơ đồ công nghệ trưng cất hoá chất
*Phân chia thành các quá trình cơ bản
Với ví dụ dây truyền hình 2. 2, đầu tiên ta có thể chia thành hai quá trình con là quá trình phản
ứng và quá trình chưng luyện tương ứng với hai công đoạn độc lập. Nếu để thiết kế sách lược điều khiển
ta có thể dừng lại ở mức độ phân chia này. Tuy nhiên, nếu cần chi tiết hơn ta có thể tiếp tục chia thành
các quá trình cơ bản tương ứng với các thiết bị quá trình như thiết bị phản ứng, tháp chưng luyện, bình
chứa, thiết bị gia nhiệt, thiết bị ngưng tụ… Việc xây dựng các phương trình có thể dễ dàng tiến hành với
các quá trình cơ bản này.
* Xây dựng các mô hình thành phần
Xây dựng mô hình toán học cho một quá trình là xác định quan hệ giữa các biến quá trình và biểu
diễn các mối quan hệ đó thông qua các phương trình vi phân hoặc phương trình đại số. Mỗi thiết bị cơ
bản thường được thực hiện trọn vẹn trong một hoặc một khối thiết bị công nghệ, vì vậy các biến vào/ra

của nó cũng là đặc trưng cho một quá trình công nghệ. Do đó việc xác định mô hình các thành phần dễ
dàng hơn.
Việc xác định các biến điều khiển, các biến điều khiển được, nhiễu và quan hệ giữa chúng phụ
thuộc vào yêu cầu, mục đích điều khiển. Sau khi đã có các phương trình mô hình, ta cần phân tích và
kiểm chứng mô hình bằng công cụ toán học và công cụ mô phỏng về tính hợp lý, tính trung thực cũng
như khả năng sử dụng của mô hình.

25

Quá trình cơ bản là các quá trình thoả mãn tính chất sau:
 Tương đối đơn giản để có thể dễ dàng mô hình hoá.
 Tiêu biểu cho nhiều quy trình công nghệ.
 Thường được thực hiện trọn vẹn trong một khối thiết bị công nghệ.
Các quá trình pha trộn/phối liệu (blending/mixing) , phản ứng (reaction) , chưng luyện
(distillation) , gia nhiệt (heating) , hoá hơi (evaporator), ngưng tụ (condensing) là một số quá trình cơ bản.
* Kết hợp các mô hình thành phần
Sau khi đã tiến hành xây dựng xong các mô hình thành phần thì công việc tiếp theo là kết hợp
chúng lại để thu được mô hình của toàn bộ quá trình công nghệ. Nguyên tắc kết hợp các mô hình thành
phần dựa trên tín hiệu vào/ra, không dựa trên dòng quá trình. Trong trường hợp có hồi lưu, trong mô hình
kết hợp sẽ có thêm các đường tín hiệu phản hồi.
* Phân tích và kiểm chứng mô hình
Sau khi kết hợp mô hình tổng hợp cần phải được phân tích và kiểm chứng chi tiết hơn những tính
chất như mức độ phi tuyến, tính ổn định, khả năng điều khiển được, mức độ tương tác giữa các biến
vào/ra. Số bậc tự do cần được xác định lại, khi mà số biến độc lập giảm đi khi kết hợp hai mô hình thành
phần có sử dụng biến chung.

2.3. Phân loại mô hình toán học
Phần lớn các quá trình công nghiệp tương đối phức tạp với các biến vào/ra, nhiều quan hệ giữa
các biến vào/ra không những phi tuyến mà còn phụ thuộc thời gian và theo thời gian. Khi xây dựng mô
hình toán học tuỳ theo mục đích và yêu cầu sử dụng, ta có thể bỏ qua nhiều khía cạnh nhằm đơn giản hoá

bài toán. Mô hình nhận được có thể không phản ánh đúng quá trình thực nhưng điều quan trọng là nó sử
dụng đúng mục đích đặt ra với các điều kiện giả thiết. Mô hình là đại diện cho một quá trình lý tưởng
được đặt ra cho quá trình kỹ thuật. Mô hình được phân loại theo tính chất kỹ thuật của từng loại hệ thống.

2.3.1. Mô hình tuyến tính và mô hình phi tuyến
Mô hình được gọi là tuyến tính khi quan hệ giữa các biến vào/ra của nó thể hiện theo nguyên lý
xếp chồng. Một cách hình thức, nếu M(u) là một toán tử truyến tính, u
1
, u
2
là biến độc lập, ta có được:
M(u
1
+ u
2
) = M(u
1
) + M(u
2
) (2.1)
khi đó nếu các tín hiệu ra y
1
, y
2
lần lượt ứng với các tín hiệu độc lập bất kỳ u
1
, u
2
, thì ta sẽ có y = y
1

+ y
2

ứng với u = u
1
+ u
2
. Ngược lại, chỉ cần bất kỳ một quan hệ vào/ ra nào không thoả mãn nguyên lý xếp
chồng thì mô hình sẽ được gọi là mô hình phi tuyến.
Trong thực tế hầu hết là các quá trình phi tuyến. Tuy nhiên tuỳ theo quan hệ mà có thể tuyến tính
hoá theo mục đích sử dụng. Chỉ khi nào mô hình không thể tuyến tính được vì đáp ứng ra sai với thực tế
thì khảo sát mô hình theo hệ phi tuyến.

26


Hình 2. 3. Minh hoạ nguyên lý xếp chồng

2.3.2. Mô hình đơn biến và mô hình đa biến
Mô hình biểu diễn quan hệ giữa một biến vào và một biến ra là mô hình đơn biến (SISO) hoặc
biểu diễn quan hệ giữa nhiều biến vào và nhiều biến ra là mô hình đa biến (MIMO). Phương trình vi
phân, hàm truyền đạt và hàm quá độ là các dạng biểu diễn các quá trình đơn biến tiêu biểu. Trong đó hàm
truyền đạt và hàm quá độ có ý nghĩa cho hệ thống tuyến tính. Các dạng mở rộng như phương trình vi
phân, ma trận truyền đạt, ma trận quá độ được sử dụng cho hệ đa biến. Phương pháp biểu diễn trong
không gian trạng thái được coi là đa năng sử dụng cho hệ đơn biến, đa biến tuyến tính và phi tuyến.

Hình 2. 4. Mô hình đơn biến và mô hình đa biến.
Mô hình đơn biến có nhiều thuận lợi khi sử dụng các phương pháp điều kinh điển cũng như sử
dụng các phương pháp điều khiển hiện đại. Một số các mô hình đơn biến tiêu biểu là các khâu bậc nhất,
bậc hai, có trễ hoặc không có trễ, các khâu quán tính tích phân, khâu dao động bậc hai.

2.3.3. Mô hình tham số hằng và mô hình tham số biến thiên
Quan hệ giữa các đại lượng đặc trưng của quá trình có thể thay đổi theo thời gian, theo điểm làm
việc và theo tác động của nhiễu. Một mô hình có quan tâm phản ánh sự thay đổi tham số phụ thuộc thời
gian và được gọi là mô hình tham số biến thiên. Ngược lại mô hình có sự thay đổi của tham số theo thời
gian không đáng kể hoặc ta chỉ quan tâm đén thời gian tương đối ngắn có thể sử dụng mô hình tham số
hằng.
Hầu hết các mô hình thiết kế chấp nhận dạng tham số hằng. Trong quá trình điều khiển sẽ chọn
các giải pháp, các hướng điều khiển thích hợp. Mô hình tuyến tính tham số hằng (Viết tắt LTI – Linear
Time – Invariant)

2.3.4. Mô hình tham số tập trung và mô hình tham số rải
Mô hình biểu diễn tính chất phân bố theo không gian được gọi là mô hình tham số rải (Distribited
– Parameter Model). Ví dụ như nhiệt độ lò nung tại những vị trí khác nhau là khác nhau hay nồng độ

27

của dung dịch trong bể trộn cũng không đồng đều tại mọi vị trí. Khi đó biến ra y không chỉ phụ thuộc và u
và thời gian mà còn phụ thuộc vào z:
y = M(u, t, z) (2.2)
Mô hình không quan tâm tới sự phân bố này được gọi là mô hình tham số tập trung (Lumped –
Parameter model) , khi đó ta có:
y = M(u, t) (2.3)
Trong thức tế tuỳ theo yêu cầu mà có thể xây dựng mô hình theo dạng tham số rải hoặc tham số
tập trung. Nhưng hầu hết ngầm hiểu các mô hình sử dụng là mô hình tam số tập trung.

2.3.5. Mô hình liên tục và mô hình gián đoạn
- Một mô hình liên tục(Continuous – time Model) mô tả quan hệ giữa các biến quá trình liên
tục theo thời gian. Nói cách khác các tín hiệu trong mô hình liên tục theo thời gian.
- Mô hình gián đoạn (Discrete – Time Model) chỉ phản ánh đặc tính quá trình tại thời điểm
nhất định (tại thời điểm quan sát)

Một mô hình liên tục chỉ thích hợp với quá trình liên tục – Các quá trình mà đặc tính của nó có thể
mô tả bằng các phương trình vi phân. Trong khi đó, mô hình gián đoạn có thể thể hiện cho tất cả các
thành phần trong hệ thống điều khiển số, cho cả quá trình và bộ điều khiển
Một mô hình gián đoạn có thể được xây dựng thông qua mô hình liên tục bằng các tín hiệu trính
mẫu hoặc được xây dựng trực tiếp thông qua nhận dạng. Hầu hết các phương pháp biểu diễn liên tục cũng
có dạng tương tự cho mô hình gián đoạn.
Để phân biệt được hai loại mô hình này thông qua sơ đồ:

Hình 2. 5. Sơ đồ hệ thống điều khiển số


28

2.4. Các dạng mô hình liên tục
2.4.1. Phương trình vi phân
Phương trình vi phân là công cụ toán học quan trọng nhất cho các hệ liên tục. Đa số mô hình đơn
biến tham số tập trung có thể đưa về biểu diễn dưới dạng phương trình vi phân thường:

),(),(
01
1
1
1
tuhuyhya
dt
dy
a
dt
yd
a

dt
yd
a
fx
n
n
n
n
n
n




(2.4)
với y là biến ra, h
x
(y, u) là hàm tương tác phi tuyến, h
f
(u, t) là hàm cưỡng bức do tác động của biến vào, a
i

là các tham số. Khi đó n được gọi là bậc của mô hình. Hai dạng phương trình đơn giản dưới đây được đặc
biệt quan tâm trong điều khiển quá trình.
Mô hình phương trình vi phân của khâu quán tính bậc nhất có trễ FOPDT (first – order plus
time) :
)t(ku)t(y
dt
)t(dy
 (2.5)

Mô hình tổng quát của khâu tuyến tính bậc hai có trễ SOPDT (Second – order plus dead-time) :
)t(ku)t(y
dt
)t(dy
2
dt
)t(yd
2
2
2
 (2.6)
trong đó k là hệ số khuyếch đại,  hằng số thời gian,  là thời gian trễ,  là hệ số tắt dần (  0).
Đối với hệ đa biến, ta sẽ có một hệ phương trình vi phân phương trình (2.4) cũng có thể mở rộng
để biểu diễn một cách tổng quá hệ đa biến:
),(),(
01
1
1
1
tyhuyhyA
y
A
y
A
y
A
fx
n
n
n

n
n
n
dt
d
dt
d
dt
d




(2.7)
trong đó y, u là các véctơ tín hiệu, A
i
là các ma trận tham số; h
x
, h
f
là các vector hàm đa biến.
Cần chú ý rằng: Phương trình vi phân có ưu điểm là khả năng biểu diễn mạnh, tuy nhiên rất khó phân
tích và thiết kế hệ thống, đặc biệt là với mô hình bậc cao. Phương pháp mô tả tổng quát và hữu hiệu là
phương trình trạng thái.

2.4.2. Mô hình trạng thái
1. Mô hình trạng thái phi tuyến
Mô hình trạng thái là hình thức mô tả tổng quát, phù hợp cho cả hệ đơn biến và hệ đa biến, tuyến
tính cũng như phi tuyến. Một quá trình với m biến vào (vector vào u) , p biến ra (vector y) và n biến trạng
thái (vector trạng thái x) có thể biểu diễn với mô hình vector trạng thái sau:

;xxuxfx
0
(0)),,( 


nmnmn
RRR:;R,  fuRx

y = g(x, u)
pmnP
RRR:,R  gy (2.8)
Trong đó f và g là các vector hàm đa biến. Phương trình thứ nhất được gọi là phương trình trạng
thái, phương trình thứ hai được gọi là phương trình đầu ra. Phương trình trạng thái thực chất là một hệ
phương trình vi phân, trong đó chỉ xuất hiện đạo hàm cấp một. Chú ý rằng từ phương trình vi phân (2.4)

29

ta cũng có thể dễ dàng đi đến dạng tổng quát bằng cách đặt vector trạng thái trung gian x. Ví dụ, nếu h
x
(y,
u) = 0 và bỏ qua thời gian t trong h
f
(u, t) , đặt véc tơ trạng thái:





















1n
1n
dt
yd
dt
dy
y

x (2.9)

ta nhận được
 
x
xx
001y
(u)h

0
0
.
a
a
a
a
a
a
1000
0
100
0010
f
n
1n
1n
1
n
0



















































(2.10)
Mô hình biểu diễn trong không gian trạng thái có rất nhiều ưu điểm. Thứ nhất mô hình trạng thái
không những thể hiện quan hệ vào/ra mà còn thể hiện cái nhìn sâu sắc hơn về hệ thống thông qua các biến
trạng thái và cấu trúc liên kết bên trong. Thứ hai, với mô hình trạng thái ta có thể tiến hành phân tích và
thiết kế hệ thống trên miền thời gian thực bằng phương pháp đại số. Thứ ba, mô hình trạng thái rất dễ
biểu diễn và thực thi trên máy tính. Chính vì thế mà các phương pháp phân tích mô hình trạng thái được
phát triển mạnh theo trường phái điều khiển hiện đại.

2. Mô hình trạng thái tuyến tính
Bản chất của bài toán điều chỉnh là duy trì trạng thái của quá trình tại một điểm làm việc cân bằng.
Như vậy thay vì mô hình phi tuyến, trong đại đa số trường hợp ta sử dụng một mô hình tuyến tính đại
diện cho quá trình trong lân cận điểm làm việc đó. Mô hình tuyến tính này có thể được xây dựng với quan
điểm xấp xỉ tuyến tính ngay từ đầu, hoặc được tuyến tính hoá từ một mô hình phi tuyến. Nếu một mô
hình trạng thái phi tuyến biểu diễn trong (2.8) có điểm cân bằng ),( ux hay 0),(


uxfx

và khả vi tại
),( ux ta có thể xấp xỉ về một mô hình tuyến tính cho phạm vi làm việc lân cận ),( ux thông qua phép
khai triển Taylor. Đặt:

xxx





uuu



(2.11)
Khai triển chuỗi Taylor và bỏ qua thành phần bậc cao, ta có:

ΔuΔx),f()Δ,Δf(Δ
,, uxux
u
f
x
f
uxuuxxxx







(2.12)

30


u)u,x(guuxxyyy
uxux
y
Δ
u
g
Δx
x
g
)Δ,Δg(Δ
,,







(2.13)
Đặt các ký hiệu ma trận
nn
,
R,





 A
x
f
A
ux

mn
,
R,
u




 B
f
B
ux

np
,
R,




 C
x
g
C

ux
(2.14)
mp
,
R,




 D
u
g
D
ux

Các ma trận A và B được gọi là ma trận Jacobi của véctor hàm f(x, u) , C và D là các ma trận Jacobi của
véctor hàm g(x,u) bất kỳ, f: R
n
 R
m
với:















n
2
1
x
x
x

x
,













m
2
1

f
f
f

f

được định nghĩa



























n
m
1
m
n
1
1
x
f
x
f
x
f
x
f



x
f

Lưu ý rằng, x, u và y hoàn toàn có thể được coi là các biến đặc trưng của hệ thống nếu như ta
lấy
u
x
,
và

y
là các điểm quy chiếu. Thực tế, với các mô hình tuyến tính ta luôn sử dụng các biến chênh
lệch thay cho các biến giá trị thực. Vì vậy, đơn giản hoá cách viết mà không sợ nhầm lẫn, ta thay lại các
ký hiệu x, u và y trở lại lần lượt bằng x, u và y:
xxxBuAxx 
0
(0),

(2.15)
y = Cx + Du

Hình2. 6. Mô hình trạng thái liên tục minh hoạ bằng sơ đồ khối.