Bài Tập Lớn Sức Bền Vật Liệu TNUT 2013

1
BÀI TẬP LỚN SỨC BỀN VẬT LIỆU


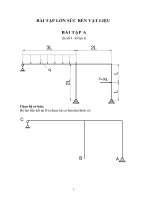
BÀI TẬP A
(Sơ đồ 8 - Số liệu 4)

q
3L
2L
L
L
P=3qL
2L

Chọn hệ cơ bản:
Bỏ hai liên kết tại B ta được hệ cơ bản như hình vẽ:

A
B
C






2

Ta có hệ tĩnh định tương đương:
Liên kết tại B có 2 thành phần phản lực theo 2 phương vuông góc. Do đó khi
bỏ liên kết đó đi ta phải đặt vào các phản lực (
11
;XY
) theo 2 phương để thay
thế ( hình vẽ )


P=3qL
q
A
B
C
X1
Y1


Vẽ Biểu Đồ Momen M
1
, M
2
,M
p
:

M1: Biểu đồ momen đơn vị do X

1
= 1 gây nên.
Đặt lực X
1
= 1 vào hệ cơ bản như hình vẽ. Xác định các phản lực liên kết tại
gối A và C

3
A
B
C
X1 X
A
Y
A
YC



11
( ) 0 0 1
i A A
x P X X X X        



( ) 0 .3 .2 0
0
( ) 0 0
CA

CA
i C A
m B Y L Y L
YY
y P Y Y

   

  

   





Sau khi xác định được các phản lực liên kết ta vẽ được biểu đồ M
1
:

A
B
C
X1=1
2L
2L
2L

4
M2: Biểu đồ momen đơn vị do Y
1
= 1 gây nên.
Đặt lực Y
1
= 1 vào hệ cơ bản như hình vẽ. Xác định các phản lực liên kết tại
gối A và C
A
B
C
Y1
X
A
Y
A
YC

 Ta có X
A
=0

1
1

2
( ) 0 .5 .2 0
5
3
( ) 0 0 1
5
C
C
i A C A C
A
qL
Y
m A Y L Y L
qL
y P Y Y Y Y Y
Y





   




        










Sau khi xác định được các phản lực liên kết tại các gối, ta vẽ được biểu đồ
M
2
:

A
B
C
Y1=1
1,2L



5
Mp: Biểu đồ momen do tải trọng đặt nên hệ cơ bản gây nên.
Xác định các phản lực liên kết tại gối A và C.
P=3qL
q
A
B
C
X
A
Y

A
Yc


( ) 0 0 3
i A A
x P X P X qL     



( ) 0 3
1,5
( ) 0 5 . 3 .1 3 .3,5 0
i A C
CA
C
y P Y Y qL
Y Y qL
m A LY qL qL L

   

  

    





Sau khi xác định được các phản lực liên kết ta vẽ được đồ thị M
p
:

A
B
C
3qL
2
1,12qL
2


6
A
B
C
2L
2L
2L
A
B
C
1,2L
A
B
C
3qL
2
1,12qL

2
(Mp)
(M2)
(M1)


7




Xác định phương trình chính tắc:

3
11 1 1
1 1 2 40
( ) ( ) 2 2 2
EJ 2 3 3
L
M M L L L
EJ


       



3
22 2 2
1 1 2 1 2 12

( ) ( ) 1,2 3 1,2 1,2 2 1,2
EJ 2 3 2 3 5
L
M M L L L L L L
EJ


            



3
12 21 1 2
1 1 12
( ) ( ) 2 2 1,2
EJ 2 5
L
M M L L L
EJ



       



4
2 2 2
11
1 1 3 1 25

( ) ( ) 3 2 2 3 2 3 2
EJ 2 4 3 2
pp
qL
M M qL L L qL L L qL L L
EJ


               



4
22
22
1 2 1 1 1 18
( ) ( ) 1,12 3 1,2 3 2 1,2
EJ 3 2 2 3 125
pp
qL
M M qL L L qL L L
EJ


            



Ta có phương trình chính tắc:
11 1 12 1 1

21 1 22 1 2
11
11
0
0
40 12 25
0
3 5 2
12 12 18
0
5 5 125
p
p
XY
XY
qL
XY
XY


     



     




  






  






8
Giải phương trình ta được:
1
1
1,16
1,22
X qL
Y qL







Sau khi xác định được 2 phản lực liên kết tại B, ta đi vẽ biểu đồ M, N, Q cho
hệ tĩnh định tương đương ( hệ siêu tĩnh ). X
1

và Y
1
đều dương vậy chiều đúng
với giả thiết.
Để vẽ được các biểu đồ nội lực thì ta đặt các lực X
1
và Y
1
vào hệ cơ bản, xác
định các giá trị nội lực tại A và C.
P=3qL
q
A
B
C
X1
Y1
X
A
Y
A
YC


11
( ) 0 0 3 1,16 1,84
i A A
x P X X P X P X qL qL qL          


1
1
( ) 0 3 0 3 1,22 1,78
3
( ) 0 .5 .2 . 3 2 0
2
1,01
0,77
i A C A C
C
C
A
y P Y Y Y qL Y Y qL qL qL
L
m A Y L Y L P L qL L
Y qL
Y qL

          



      













Sau khi xác định được các phản lực liên kết tại gối A và C, ta vẽ được biểu
đồ M, Q, N cho hệ TDTD như hình sau :

9
1,16qL
0,77qL
1,22qL
Nz
Qy
Mx
0,77qL
1,84qL
1,16qL
1,16qL
1,99qL
1,01qL
0,68qL
2
1,84qL
2
2,32qL
2
0,86qL
2
1,46qL

2
0,51qL
2


10


CÂN BẰNG NÚT:

3L
2L
L
L
P=3qL
2L
q
A
B
C
D
E

1. Xét nút E:


0x 




0
p
m 


 Nút cân bằng

1,16qL
1,16qL
0,68qL
2
0,68qL
2
E



11









2. Xét nút D:

0,68qL

2
0,68qL
2
0,68qL
2
1,99qL
0,77qL
1,16qL
1,16qL
1,22qL
D



0x 



0
p
m 


=> Nút cân bằng

12
BÀI TẬP B
(Sơ đồ 8 – số liệu 4)
Phần I: Sơ đồ hóa
I. Thiết lập bản vẽ tính toán.
- Đặt lực tại vị trí ăn khớp.
- Chuyển lực về đường trục.

A

2
P

2
T
1
T

2
3t
P
1
M
d
M

a2
M
1
M
2
A
D
B
C
Z
2
Z
'
2
Z
1
Z
'
1
P

2
A

2
T

2
t
2t

P
1
T
1
2a
a a
a a
Mx
My
Mz


13

- Phân lực về các mặt phẳng:
o Mặt phẳng thẳng đứng yOz
o Mặt phẳng nằm ngang xOz
o Mặt phẳng xOy
II. Xác định giá trị các lực.
1. Tại vị trí bánh đai:
- Momen gây xoắn:
( ) 10
9550 ( . ) 9550 382( . )
( / ) 250
D
N Kw
M N m N m
n v ph
  

- Lực căng đai:
2
2.382
1528( )
0,5
D
M
tN
D
  

3t = 3.1528 = 4584 (N)
2. Tại vị trí bánh răng trụ răng thẳng Z
1
:
- Momen gây xoắn: (Bỏ qua tổn thất do ma sát)
1
127,3( . )
3
D
M
M N m

- Lực tiếp tuyến:
1
1
1
2
2.127,3
2546( )

0,1
M
PN
D
  

- Lực hướng kính:
11
0,364 0,364.2546 926,7( )T P N  

3. Tại vị trí bánh răng nón Z
2
:
- Momen gây xoắn: ( Bỏ qua tổn thất do ma sát)
2
2
254,7( . )
3
D
M
M N m

- Lực tiếp tuyến:
2
2
2
2
2.254,7
2830( )
0,18

M
PN
D
  

- Lực hướng kính :
22
0,364. 0,364.2830 1030( )T P N  


14
- Lực dọc trục:
22
. 0,14.2830 396,2( )A k P N  

- Momen do lực dọc trục gây lên:
22
2
.
144,2.0,18
35,66( . )
22
a
AD
M N m  
2

PHẦN II: VẼ BIỂU ĐỒ MOMEN CHO DẦM SIÊU TĨNH
I. Vẽ biểu đồ momen M
x

st
Cắt bỏ mút thừa và chuyển lực về gần gối lân cận, được một lực và một
momen M
2

Như vậy ra có dầm liên tục với bậc siêu tĩnh n = 1.
1. Hệ cơ bản hợp lí: Tưởng tượng cắt dời dầm tại vị trí các gối và nối
chúng lại bằng một khớp, ta giải phóng được liên kết chống xoay.
2. Hệ tĩnh định tương đương.
Đặt tải trọng và mô men liên kết tại khớp. Với điều kiện góc xoay tương
đối giữa 2 mặt cắt sát khớp bằng không, ta được hệ tĩnh định tương đương.
3. Phương trình 3 mômen

1 1 2 2
1 1 2 1 2 2
12

. 2( ) . 6 0
o
ab
l M l l M l M
ll


     



Trong đó: l
1

= 4.70 = 280 mm l
2
= 2.70=140mm
M
o
= 0 M
2
= 0
1 1 2 2
12
11
0,28 198,1 0,14 0,14 32,43 0,07

22
6 6 90
0,28 0,14
ab
ll

     



     





Thay vào phương trình 3 mô men và giải ra ta được: M

1
= 107,14 N.m
4. Vẽ biểu đồ mô men:
- Thay giá trị mô men M
1
vào hệ tĩnh định tương đương.
- Vẽ biều đồ mômen M
1

- Vẽ biểu đồ mômen M
2

- Áp dụng nguyên lí cộng tác dụng, vẽ biểu đồ M
x
st




15
Biểu đồ M
x
st
:


A

2
P

2
T
1
M
0
M
1
M
1
M
2
2a 2a a a
198,10
32,43
53,57
107,14
53,57
144,53
107,14
21,14
HTDTD
M
P
M
1
M
St
X
HCB

16
II. Vẽ biểu đồ mômen M
y
st
:
Cắt bỏ mút thừa và chuyển lực về gối lân cận, được 1 lực và 1 mômen
M
2
. Như vậy ta có dầm liên tục với bậc siêu tĩnh n = 1.
1. Hệ cơ bản hợp lí: Tưởng tượng cắt dời dầm tại vị trí các gối và nối
chúng lại bằng một khớp, ta giải phóng được liên kết chống xoay.
2. Hệ tĩnh định tương đương:
Đặt tải trọng và mô men liên kết tại khớp. Với điều kiện góc xoay tương
đối giữa 2 mặt cắt sát khớp bằng không, ta được hệ tĩnh định tương đương.
3. Phương trình 3 mômen:
1 1 2 2
1 1 2 1 2 2
12

. 2( ) . 6 0
o
ab
l M l l M l M
ll


     



Trong đó: l
1
= 280mm l
2
= 140mm
M
o
= 0 M
2
= 0
1 1 2 2
12
12
0,14 250,37 0,14 0,07 214,71 0,175
23
1 2 1
0,07 (267,8 214,71) 0,14 0,07 0,07 267,8 0,23

2 3 2

66
0,28
1
0,14 89,11 0,07
2
0,14
128,18
ab
ll

      




         











  

 




Thay vào phương trình 3 mô men và giải ra ta được:
M
1
= -152,5(N.m)
4. Vẽ biểu đồ mô men:
- Thay giá trị mô men M
1
vào hệ tĩnh định tương đương.
- Vẽ biều đồ mômen M
1

- Vẽ biểu đồ mômen M
2

- Áp dụng nguyên lí cộng tác dụng, vẽ biểu đồ M
y
st



17
Biểu đồ M
y
st
:

P
1
M
a2
T

2
3t
2a
a a aa
M
0
M
1
M
1
M
2
89,11
214,71
250,37
267,8
152,5
152,5
165,36
153,43
174,12
114,37
76,25
76,25

HTDTD
HCB
M
P
M
1
M
St
Y
138,46






18




III. Vẽ biểu đồ mômen M
z
st
:
Dựa vào sơ đồ lực, ta vẽ được biểu đồ M
z
st
trên hình vẽ:

M
d
M
1
M
2
2a a a aa
254,7
127,3
127,3
HTDTD
M
St
Z

19
Phần III: Xác Định Đường Kính Trục Siêu Tĩnh

Dựa vào các biểu đồ mômen trên hình vẽ ta có:
144,53
107,14
21,14
M
St
X
152,5
165,36
153,43
174,12
M
St
Y
254,7
127,3
127,3
M
St
Z
18,64
138,46
A
D
B
C

E
F


1. Xác định mặt cắt nguy hiểm:
Theo thuyết bền thế năng biến đổi hình dạng cực đại, ta có:
2 2 2
0,75.
td x y z
M M M M  

Áp dụng công thức ta có:
Tại A: M
td
= 0

20
Tại E:
22
2 2 2
( ) 144,53 174,12 226,29 .
( ) 144,53 174,12 0,75.254,7 316 .
td trai
td phai
M E N m
M E N m
  
   

Tại D:
2 2 2
2 2 2
( ) 18,64 153,43 0,75.254,7 269,3 .
( ) 18,64 153,43 0,75.127,3 189,8 .
td trai
td phai
M D N m
M D N m
   
   


Tại B:
2 2 2
( ) 107,14 152,5 0,75.127,3 216,5 .
td
M B N m   


Tại F:
2 2 2
22
( ) 21,14 165,36 0,75.127,3 199,86 .
( ) 21,14 165,36 166,7 .
td trai
td phai
M F N m
M F N m
   

  

Tại C: M
td
= 0

Mặt cắt nguy hiểm là mặt cắt có M
td
lớn nhất. Theo kết quả tính trên, ta có
mặt cắt nguy hiểm là mặt đi qua điểm E
phai
có M
td
= 316(N.m)
2. Xác định đường kính:
Theo điều kiện bền ta có:

3
[]
W 0,1.
td td
td
x
MM
d

  

Cho nên:

max
3
3
6
316
0,0165( ) 16,5( )
[ ] 70.10
td
M
d m mm

   













21
Phần IV: Xác Định Chuyển Vị Tại Điểm Lắp Bánh Răng Z
2

1. Tính chuyển vị theo phương thẳng đứng f

y

Theo phép nhân biểu đồ Varesaghin, ta có:
( ).( )
st cb
y x kx
f M M

Vẽ biểu đồ M
x
st
(Hình vẽ).
Tại điểm cần tính chuyển vị, ta đặt lực P
k
= 1 theo phương thẳng đứng lên hệ
cơ bản và coi đó là tải trọng, vẻ biểu đồ momen đơn vị ( Hình vẽ).
Tính chuyển bị:
1
( ).( ) ( )
EJ
st cb
y x kx
x
f M M

Với J
x
= 0.05d
4
= 0,05.0,0165

4
= 3,7.10
-9
; E = 2.10
11
(N/m
2
)

144,53
107,14
21,14
M
St
X
18,64
P
k
=1
0,07
0,035
M
cb
k


Ta có:
9 11
1 1 2 1 2
144,53.0,14. 0,07 .0,14.(144,53 107,14). 0.07 107,14.0,14.0,035

3,7.10 .2.10 2 3 2 3
y
f



   



=> f
y
= -1,04.10
-3


2. Tính chuyển vị theo phương thẳng đứng f
x

Theo phép nhân biểu đồ Varesaghin, ta có:
( ).( )
st cb
x y ky
f M M


22
Vẽ biểu đồ M
y
st

(Hình vẽ).
Tại điểm cần tính chuyển vị, ta đặt lực P
k
= 1 theo phương thẳng đứng lên hệ
cơ bản và coi đó là tải trọng, vẻ biểu đồ momen đơn vị ( Hình vẽ).
Tính chuyển bị:
1
( ).( ) ( )
EJ
st cb
x y ky
y
f M M

Với J
y
= 0.05d
4
= 0,05.0,0165
4
= 3,7.10
-9
; E = 2.10
11
(N/m
2
)

P
k

=1
0,07
0,035
M
cb
k
152,5
165,36
174,12
M
St
Y
138,46
153,43


Ta có:
9 11
1 2 3 1 2
.0,14.174,12. .0,07 138,46.0,07. 0.07 0.07.(153,43 138,46) .0,07
1
2 3 4 2 3
1 1 1
3,7.10 .2.10
(152,5 153,43).0,07. 0,07 0,07.152,5. .0,035
2 3 2
x
f



  




  


=> f
x
= 1,57.10
-3


3. Tính chuyển vị toàn phần:

2 2 3
1,88.10
xy
f f f

  