Bài giảng lý thuyết điều khiển tự động - Khảo sát tính ổn định của hệ thống part 6 docx

26 September 2006 © H. T. Hồng - ÐHBK TPHCM 51
Phương pháp quỹ đạo nghiệm số (QĐNS)
Phương pháp quỹ đạo nghiệm số (QĐNS)
Thí dụ 4
Thí dụ 4
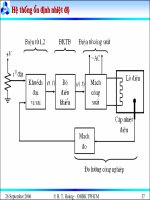
 Cho hệ thống điều khiển có sơ đồ khối như sau:
)39(
10
)(
2
++
=
ss
sG
s
K
KsG
I
PC
+=)(
 Cho K
I
= 2.7, hãy vẽ QĐNS của hệ thống sau đây khi K
P
=0→+∞,
biết rằng dK
P
/ ds=0 có 3 nghiệm là −3, − 3, 1.5.
 Khi K
P
=270, K

I
= 2.7 hệ thống có ổn đònh hay không?
26 September 2006 © H. T. Hồng - ÐHBK TPHCM 52
Phương pháp quỹ đạo nghiệm số (QĐNS)
Phương pháp quỹ đạo nghiệm số (QĐNS)
Thí dụ 4 (tt)
Thí dụ 4 (tt)
 Các zero:
0
1
=z
 Giải:
 Phương trình đặc trưng của hệ thống:
0)()(1
=
+ sGsG
C
(1)
0
)3)(9(
10
1
2
=
++
+
ss
sK
P
⇔

0
39
107.2
1
2
=






++






++
ss
s
K
P
⇔
 Các cực:
9
1
−=p
3

2
jp +=
3
3
jp −=
26 September 2006 © H. T. Hồng - ÐHBK TPHCM 53
Phương pháp quỹ đạo nghiệm số (QĐNS)
Phương pháp quỹ đạo nghiệm số (QĐNS)
Thí dụ 4 (tt)
Thí dụ 4 (tt)
 Tiệm cận:
 Điểm tách nhập:
1)(l 2/
0)(l 2/

13
)12()12(
−=−
=
⇒
−
+
=
−
+
=
π
π
ππ
α

l
mn
l
0=
ds
dK
P
2
9
13
)0()]3()3(9[
zero
−=
−
−−++−
=
−
−
=
∑
∑
jj
mn
OA
cực
(loại)






=
−=
−
=
5.1
3
3
3
2
1
s
s
s
⇔
QĐNS có hai điểm tách nhập trùng nhau tại −3
26 September 2006 © H. T. Hồng - ÐHBK TPHCM 54
Phương pháp quỹ đạo nghiệm số (QĐNS)
Phương pháp quỹ đạo nghiệm số (QĐNS)
Thí dụ 2 (tt)
Thí dụ 2 (tt)
 Góc xuất phát của QĐNS tại cực phức p
2
:
)]arg()[arg()arg(180
321212
0
2
ppppzp −+−−−+=
θ







+








−
−+=
−
90
9
3
90180
10
tg
0
2
169−=
θ
))]3(3arg())9(3[arg()03arg(180
0

jjjj −−+−−−−+=
26 September 2006 © H. T. Hồng - ÐHBK TPHCM 55
Phương pháp quỹ đạo nghiệm số (QĐNS)
Phương pháp quỹ đạo nghiệm số (QĐNS)
Thí dụ 4 (tt)
Thí dụ 4 (tt)
 Khi K
I
=2.7, QĐNS của
hệ thống nằm hoàn
toàn bên trái mặt phẳng
phức khi K
P
=0→+∞,
do đó hệ thống ổn đònh
khi K
I
=2.7, K
P
=270.
26 September 2006 © H. T. Hồng - ÐHBK TPHCM 56
Tiêu chuẩn ổn đònh tần số
Tiêu chuẩn ổn đònh tần số
26 September 2006 © H. T. Hồng - ÐHBK TPHCM 57
Tiêu chuẩn ổn đònh tần số
Tiêu chuẩn ổn đònh tần số
Khái niệm đặc tính tần số
Khái niệm đặc tính tần số
 Hãy quan sát đáp ứng của hệ thống tuyến tính ở trạng thái xác
lập khi tín hiệu vào là tín hiệu hình sin.

26 September 2006 © H. T. Hồng - ÐHBK TPHCM 58
Tiêu chuẩn ổn đònh tần số
Tiêu chuẩn ổn đònh tần số
Khái niệm đặc tính tần số
Khái niệm đặc tính tần số
 Hệ thống tuyến tính: khi tín hiệu vào là tín hiệu hình sin thì ở
trạng thái xác lập tín hiệu ra cũng là tín hiệu hình sin cùng tần số
với tín hiệu vào, khác biên độ và pha.
 Đònh nghóa: Đặc tính tần số của hệ thống là tỉ số giữa tín hiệu ra
ở trạng thái xác lập và tín hiệu vào hình sin .
)(
)(
ω
ω
jR
jC
=
số tần tính Đặc
Người ta chứng minh được:
)()(
ω
ω
jGsG
js
=
=
=
so
á
tầntínhĐặc

26 September 2006 © H. T. Hồng - ÐHBK TPHCM 59
Tiêu chuẩn ổn đònh tần số
Tiêu chuẩn ổn đònh tần số
Đáp ứng biên độ
Đáp ứng biên độ
–
–
Đáp ứng pha
Đáp ứng pha
 Tổng quát G(j
ω
) là một hàm phức nên có thể biểu diễn dưới
dạng đại số hoặc dạng cực:
)(
).()()()(
ωϕ
ωωωω
j
eMjQPjG =+=
Trong đó:
)()()()(
22
ωωωω
QPjGM +==
Đáp ứng biên độ







=∠=
−
)(
)(
)()(
1
ω
ω
ωωϕ
P
Q
tgjG
Đáp ứng pha
 Ý nghóa vật lý:
 Đáp ứng biên độ cho biết tỉ lệ về biên độ (hệ số khuếch đại)
giữa tín hiệu ra và tín hiệu vào theo tần số.
 Đáp ứng pha cho biết độ lệch pha giữa tín hiệu ra và tín hiệu
vào theo tần số.
26 September 2006 © H. T. Hồng - ÐHBK TPHCM 60
Tiêu chuẩn ổn đònh tần số
Tiêu chuẩn ổn đònh tần số
Biểu đồ Bode
Biểu đồ Bode
–
–
Biểu đồ Nyquist
Biểu đồ Nyquist
 Biểu đồ Bode: là hình vẽ gồm 2 thành phần:
 Biểu đồ Bode về biên độ: là đồ thò biểu diễn mối quan hệ giữa

logarith của đáp ứng biên độ L(
ω
) theo tần số
ω
 Biểu đồ Bode về pha: là đồ thò biểu diễn mối quan hệ giữa
đáp ứng pha
ϕ
(
ω
) theo tần số
ω
.
Cả hai đồ thò trên đều được vẽ trong hệ tọa độ vuông góc với
trục hoành
ω
được chia theo thang logarith cơ số 10.
)(lg20)(
ω
ω
M
L
=
[dB]
 Biểu đồ Nyquist: (đường cong Nyquist) là đồ thò biểu diễn đặc
tính tần số G(j
ω
) trong hệ tọa độ cực khi
ω
thay đổi từ 0→∞.