Đồ án lý thuyết điều khiển tự động

Đồ án lý thuyết điều khiển tự động
LỜI NÓI ĐẦU
Trong quá trình công nghiệp hóa hiện đại hóa đất nước hiện nay, Tự Động
Hóa có mặt ngày càng nhiều trong các nhà máy, xí nghiệp và trong đời sống hàng
ngày. Trong công nghiệp, Tự Động Hóa làm tăng năng xuất, chất lượng sản phẩm
với thời gian ngắn nhất mà lại tốn ít nhân công. Trong đời sống, nó làm cho cuộc
sống của con người tiện nghi hơn.
Để các dây truyền Tự Động Hóa hoạt động ổn định, hiều quả, chúng ta cần
xác định các thông số, các chỉ tiêu chất lượng, thiết kế cấu trúc hệ thống một cách
tối ưu và đặc biệt phải thiết kê bộ điều khiển giúp cho hệ thống hoạt động ổn định
và chính xác.
Giựa trên những phương pháp hiện đại của lí thuyết điều khiển tự động. Đồ án
này của em sẽ nêu ra các cách nhận dạng đối tượng, xác định hàm truyền đạt của
đối tượng từ đáp ứng đầu ra cho trước và từ đó xác định đối tượng có ổn định hay
không.Thiết kế các bộ điều khiển P, PI, PID để nâng cao chất lượng đầu ra của hệ
thống.
Trong quá trình thực hiện đồ án em cũng đã nhận được nhiều sự giúp đỡ thầy
cô và các bạn trong lớp đã có nhưng góp ý cho đồ án của em hoàn thiện hơn.
Mặc dù rất cố gắng nhưng do kiến thức còn hạn chế nên không tránh khỏi
những thiếu sót. Rất mong nhận được nhiều hơn nữa sự đóng góp, bổ xung ý kiến
của thầy cô và các bạn để cho đồ án này ngày càng hoàn thiện hơn.
Em xin cảm ơn cô giáo Phạm Thị Hương Sen ,người đã giúp đỡ em trong
suốt thời gian làm đồ án này.
Em xin trân thành cảm ơn !!!
1
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đồ án lý thuyết điều khiển tự động
MỤC LỤC
2
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đồ án lý thuyết điều khiển tự động

ĐỀ BÀI
(Stt.20) Cho đối tượng cần điều khiển là động cơ điện 1 chiều kích từ độc lập,
biết rằng nếu phần ứng động cơ được cấp nguồn điện xoay chiều 220v, với điện áp
đặt U
d
=10V, tốc độ định mức của động cơ là 2000 vòng/phút, ( điện áp mạch kích
từ là định mức, chế độ không tải). Bằng phương pháp thực nghiệm người ta cấp
điện áp đặt U
d
=5V cho động cơ, tiến hành đo tốc độ của động cơ và ghi lại giá trị
trung bình vào bảng sau:
t[s] 0 50 100 150 200 250 300 350 400 500
n[vòng/ph
]
0 300 580 750 850 920 960 980 990 1000

Yêu cầu:
1. Xây dựng mô hình toán học của động cơ điện từ bảng số liệu trên.
2. Từ mô hình toán học thu được dùng Matlab vẽ lại đáp ứng đầu ra, so sánh
và chỉnh lại mô hình cho chính xác. Nhận xét về tính ổn định của đối
tượng.
3. Thiết kế bộ điều khiển động cơ theo các luật điều khiển sau:
• Điều khiển ON/OFF
• Điều khiển P, PI, PID tiến hành chỉnh định theo ít nhất 3 phương pháp
đánh giá chất lượng so sánh két quả thu được
3
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đồ án lý thuyết điều khiển tự động
Chương 1: XÂY DƯNG MÔ HÌNH TOÁN HỌC
I, Hàm truyên đạt ,đặc tinh động học của hệ thống

1, Hàm truyền đạt
Hàm truyền đạt của hệ thống là tỷ số của tín hiệu ra với tín hiệu vào của hệ thống
đó. Biểu diễn theo biến đổi laplace với điều kiện đầu vào bằng 0
Dạng tổng quát của hàm truyền đạt
111Equation Chapter (Next) Section 1212Equation Chapter (Next) Section 1
W(s)=
( )
( )
B s
A s
=
1
0 1 1
1
0 1 1
m m
m m
n n
n n
s
s
b s b s b b
a s a s a a
−
−
−
−
+ + + +
+ + + +
L

L
Trong đó
- Thông thường m≤n
- Khi :B(s)=0 ta có các điểm zero
- Khi :A(s)=0 ta có các điểm cực ,các nghiệm này sẽ quyết định trực tiếp tới tính
chất của hệ (A(s)=0 gọi là phương trình đặc trưng của hề thống )
2, Đặc tính độngcủa hệ thống
Đặc tính động học của hệ thống mô tả sự thay đổi tín hiệu đầu ra của hệ thống theo
thời gian khi có tác động của đầu vào
Để khảo sát tính động học của hệ thống thì tín hiệu vào thường được lựa chọn là tín
hiệu cơ bản như xung đizắc ,hàm bậc thang đơn vị ,hàm điều hòa .Tùy theo dạng của tín
hiệu vào thử mà đặc tính động học là đặc tính thời gian hay đặc tính tần số
4
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đồ án lý thuyết điều khiển tự động
2.1, Đặc tính thời gian
a, Hàm quá độ
Hàm quá độ h(t) là hàm mô tả tín hiệu đầu ra theo thời gian khi tác động đầu vào là
1(t)
b, Đặc tính hàm trọng lượng g(t)
Mô tả sự thay đổi đầu ra là hàm g(t)khi tín hiệu đầu vào là xung đizắc
2.2, Đặc tính tần số
Mô tả sự thay đổi của tỷ số biên độ tín hiệu ra và tín hiệu vào ,sự thay đổi góc pha
giữa tín hiệu ra và tín hiệu vào theo tác động tần số thay đổi
Hàm truyền tần số là
( )
W j
ω
Thay s=jω vào hàm truyền đạt
Đặc tính biên độ tần số A(ω)

Đặc tính pha tần số
5
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đồ án lý thuyết điều khiển tự động
Đặc tính nyquist là mô tả đường đặc tính W(jω)
Đường đặc tính đồ thị bode;là đường đặc tính tần biên pha trên tham logarit
II, Cách xác định hàm truyền
2.1, Các dạng hàm quá độ:
Trên cơ sở hàm quá độ của đối tượng có thể xác định gần đúng hàm truyền đạt của
nó
a, Khâu dao động bậc 2 không có trễ
Hàm truyền có dạng
b, Khâu dao động bậc 2 có trễ
Hàm truyền có dạng
2 2
W( )
2 1
s
K
s e
T s Ts
τ
ε
−
=
+ +
c, Khâu quán tính bậc 1 không trễ
6
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
0 10 20 30 40 50 60 70

0
10
20
30
40
50
60
70
80
90
100
Step Response
Time (sec)
Amplitude
0 50 100 150 200 250 300 350
0
10
20
30
40
50
60
Step Response
Time (sec)
Amplitude
0 100 200 300 400 500 600 700 800 900
0
5
10
15

20
25
30
35
40
Step Response
Time (sec)
Amplitude
Đồ án lý thuyết điều khiển tự động
Hàm truyền có dạng
( )
W
1
K
s
Ts
=
+
d, Khâu quán tính bậc 1 có trễ
Hàm truyền có dạng
W( )
1
s
K
s e
Ts
τ
−
=
+

e, Khâu quán tính bậc 2 không trễ
Hàm truyền có dạng
( ) ( )
1 2
W( )
1 1
K
s
T s T s
=
+ +
7
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
0 100 200 300 400 500 600 700 800 900
0
5
10
15
20
25
30
35
40
Step Response
Time (sec)
Amplitude
0 5 0 100 1 5 0 20 0 250 30 0 350 4 0 0 450 5 0 0
0
1 0
2 0

3 0
4 0
5 0
6 0
7 0
8 0
S te p Re s po n s e
Time ( s e c )
A m plitu d e
Đồ án lý thuyết điều khiển tự động
g, Khâu quán tính bậc 2 có trễ
Hàm truyền có dạng
( ) ( )
1 2
W( )
1 1
s
K
s e
T s T s
τ
−
=
+ +
Chú ý: Hàm quá độ của khâu quán tính
bậc 1 và khâu quán tính bậc 2 rất giống nhau
2.2 cách xác định hàm truyền:
Từ bảng số liệu ta sử dụng matlab vẽ đồ thị:
Trong cửa sổ command window gõ:
>> x=[0 50 100 150 200 250 300 350 400 500];

>> y=[0 300 580 750 850 920 960 980 990 1000];
>> plot(x,y);
0 50 100 150 200 250 300 350 400 450 500
0
100
200
300
400
500
600
700
800
900
1000
Đồ thị thu được
8
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
0 100 200 300 400 500 600
0
10
20
30
40
50
60
70
80
Step Response
Time (sec)
Amplitude

Đồ án lý thuyết điều khiển tự động
Từ đồ thị ta xác định đây là khâu quán tính bậc 2 không trễ
Hàm truyền đạt dạng tổng quát:

là hàm số chuẩn :=
Sử dụng phương pháp đồ thị giải tích để xác định các tham số , từ hàm quá độ .Kẻ
đường tiếp tuyến với đường của tại điểm uốn,ta xác định được điểm , 2 ;Xác định được
các khoảng cách a,b,c như hinh. Ta sẽ xác định , theo a,b,c.
Ta có đồ thị của
0 50 100 150 200 250 300 350 400 450 500
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
b
a
c
Ta có:
(t) = 1 - . + . (*)
(t) = ( - )
(t) = ( - )
Tại điểm uốn :
() =0  (**)

9
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đồ án lý thuyết điều khiển tự động
Từ đồ thị ta thấy : b=1 -()
Kết hợp với (*): b= . - .
Thay (**) vào: b = ( - ) = .
Ta có : a = =
Từ đồ thị ta thấy :c = 1 -()
 c = . - .
 c = ( - ) = .
Biến đổi để tìm theo a,b,c :

= =
 =
 +0,5 = =
 = a( +0,5 )
 = a - = a(0,5 - )
Với các khoảng cách a,b,c .Xác định trực tiếp trên đồ thị ta sẽ tính được các tham số
, .
Từ đồ thị ta xác định đc các giá trị a,b,c :
Áp dụng công thức:
T
1
= a( +0,5 )
T
1
= 91
T
2
= a – T

1
= 110 – 91 = 19
Như vậy ta xác định được hàm truyền đạt:
10
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đồ án lý thuyết điều khiển tự động
Chương 2: CHỈNH ĐỊNH MÔ HÌNH TOÁN HỌC VÀ NHẬN XÉT
TÍNH ỔN ĐỊNH CỦA HỆ
I. Chỉnh định
1.1, Vẽ đáp ứng đầu ra
Ta sử dụng Simulink xây dựng mô hinh hệ thống như sau:
Trong cửa sổ command windows gõ lệnh
>> plot(ScopeData.time, ScopeData.signals.values);
Ta được đáp ứng đầu ra:
0 50 100 150 200 250 300 350 400 450 500
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
11
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
0 50 100 150 200 250 300 350 400 450 500
0

100
200
300
400
500
600
700
800
900
1000
Đồ án lý thuyết điều khiển tự động
1.2, So sánh và chỉnh định lại mô hình toán học
a, So sánh
Trong cửa sổ command window gõ:
>> x=[0 50 100 150 200 250 300 350 400 500];
>> y=[0 300 580 750 850 920 960 980 990 1000];
>> plot(ScopeData.time, ScopeData.signals.values,x,y);
Ta được đồ thị của mô hình so với đồ thị đề bài:
Ta thấy 2 đường gần như trùng nhau nên đây có thể là mô hình toán học tốt nhất
b, Chỉnh định:
Tìm các hệ số T
1
và T
2
sao cho đáp ứng đầu ra của là giống đồ thị đề bài cho nhất
Phương pháp: tăng, giảm lần lượt các số T
1
và T
2
để thấy sự thay đổi của đáp ứng

đầu ra mô hình toán học
12
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đáp ứng đầu ra
0 50 100 150 200 250 300 350 400 450 500
0
100
200
300
400
500
600
700
800
900
1000
0 50 100 150 200 250 300 350 400 450 500
0
100
200
300
400
500
600
700
800
900
1000
Đồ án lý thuyết điều khiển tự động
- Khi tăng T

1
hoặc T
2
hoặc tăng cả 2 đồ thị đầu ra sẽ có dạng
- Khi giảm T
1
,

T
2
hoặc cả 2 ta được đồ thị
13
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đáp ứng đầu ra
Đáp ứng đầu ra
0 50 100 150 200 250 300 350 400 450 500
0
100
200
300
400
500
600
700
800
900
1000
Đồ án lý thuyết điều khiển tự động
Bằng phương pháp thực nghiệm ta tìm được bộ số T
1

,

T
2
tốt nhất:
Nhận xét:
+) Từ hình hai đồ thị của hàm quá độ và đặc tính ra trên một hệ trục tọa độ ta thấy
về biên độ gần giống nhau có thể chấp nhận được.
+) Sự khác nhau là do sai số làm tròn và không thể xác định chính xác được bằng
thủ công. Đường cong sau khi vẽ lại nhẵn hơn là do chọn bước nhảy của tham số đầu vào
nhỏ hơn.càng xác định chính xác thì ta càng có hàm truyền chuẩn theo như đường đặc
tính mong muốn.
Vậy ta thu được mô hình toán học
14
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đáp ứng đầu ra
Đồ án lý thuyết điều khiển tự động
II, Phân tích tính ổn định:
2.1, Điều kiện để hệ thống ổn định
Một hệ thống tuyến tính liên tục được gọi là ổn định nếu quá trình quá độ của nó tắt
dần theo thời gian, không ổn định nếu quá trình quá độ của nó tăng dần theo thời gian và
ở biên giới ổn định nếu quá trình quá độ của nó dao động với biên độ không đổi hoặc
bằng hằng số.
Đồ thị mô tả sự ổn định của hệ thống
(1): Hệ thống ổn định và không dao động.
(2): Hệ thống ổn định và dao động.
(3): Hệ thống không ổn định và không dao động.
(4): Hệ thống không ổn định và dao động.
(5): Hệ thống dao động với biên độ không đổi(biên giới ổn định)
Ổn định của hệ tuyến tính

Để biết hệ thống ĐKTĐ có ổn định hay không, ta phải giải PTDT của hệ thống có
dạng:
15
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đồ án lý thuyết điều khiển tự động
Phương trình trên có nghiệm như sau:
+Hệ thống ổn định nếu tức là có nghiệm nằm bên trái trục ảo
+Hệ ở biên giới ổn định nếu tức là có nghiệm ở trên trục trục ảo
+Hệ không ổn định nếu tức là có nghiệm nằm bên phải trục ảo
*Chỉ cần 1 nghiệm của phương trình đặc tính có phần thực dương thì hệ thốn không
ổn định.
Các nghiệm của phương trình đặc tính
Áp dụng với mô hình toán học thu được
Ta có phương trình đặc tính:

Phương trình có 2 nghiệm là:
Vậy hệ ổn định
2.2, Tiêu chuẩn ổn định Routh
Điều kiện cần thiết để một hệ thống điều khiển tuyến tính ổn định là các hệ số của
phương trình đặc trưng dương. Khi không tồn tại điều kiện cần thì hệ thống được liệt vào
loại có cấu trúc không ổn định, và lúc đó ta phải thay đổi cấu trúc của nó.
16
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đồ án lý thuyết điều khiển tự động
Điều kiện cần và đủ để hệ thống tuyến tính ổn định là tất cả các số hạng trong cột
thứ nhất của bảng Routh dương.
Cách lập bảng Routh:
+ Dòng đầu tiên của bảng Routh ghi các số hạng có chỉ số chẵn, dòng thứ hai ghi
các số hạng có chỉ số lẻ.
+ Mỗi số hạng trong một hàng của bảng Routh là một số âm có giá trị là một định

thức bậc hai với cột thứ nhất là cột thứ nhất của hai hàng ngay sát trên hàng có số hạng
đang tính; cột thứ hai là hai hàng ngay sát trên và nằm bên phải hàng có số hạng đang
tính.
+ Bảng Routh sẽ kết thúc khi nào dòng cuối cùng chỉ còn một số hạng.
Ta có bảng routh
Cách tính các hệ số của bảng Routh:

Có phương trình đặc tính như sau:
Vậy
17
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
a
0
a
2
a
4
A
6
…
a
1
a
3
a
5
a
7
…
b

0
b
2
b
4
b
6
…
b
1
b
3
b
5
b
7
…
C
0
C
2
C
4
C
6
…
C
1
C
3

C
5
C
7
…
… … … … …
Đồ án lý thuyết điều khiển tự động
Ta có bảng
Ta thấy là tất cả các số hạng trong cột thứ nhất của bảng Routh dương vì vậy hệ
thống ổn định
2.3, Tiêu chuẩn HURWITZ.
Định thức HURWITZ được thành lập từ các hệ số ai của phương trình đặc tính A(p)
và được thực hiện theo các bước sau:
B1:Ma trận HURWIT là một ma trận vuông cỡ n x n
B2:Đường chéo của ma trận là các hệ số từ a
1
tới a
n
B3:Hàng lẻ của ma trận chỉ gồm các hệ số có chỉ số lẻ tăng theo thứ rự từ trái qua
phải.
B4:Hàng chẵn của ma trận chỉ gồm các hệ số chẵn tăng theo thứ tự từ trái qua phải
Ta có bảng ma trận HURWITS
Điều kiện cần và đủ để hệ điều khiển tuyến tính ổn định là các hệ số ai của phương
trình đặc tính dương và các giá trị định thức HURWITZ dương. Tức là:
Δ
1
=a
1
>0; Δ
2

=>0; Δ
3
=>0; …
Với Δ
n
là định thức có n hàng, n cột đầu tiên:
Δ
i
>0, i=; Δ
n
=a
n
*Δ
n-1
18
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
111
Đồ án lý thuyết điều khiển tự động
 Áp dụng
Có phương trình đặc tính như sau:
Vậy
Ta được bảng ma trận HURWITZ:


 Vậy hệ ổn định
19
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Wh(s)
Wph(s)
r(t)

E(t)
Y(t)
(-)
Đồ án lý thuyết điều khiển tự động
CHƯƠNG 3: TỔNG HỢP BỘ ĐIỀU KHIỂN
I, Các chỉ tiêu đánh giá chất lượng
1.1. Đánh giá chất lượng ở trạng thái xác lập.
+) Sai số xác lập()
Xét hệ có sơ đồ tổng quát như hình bên
Ta có: E(t)=r(t)-Y(t)
+) Đánh giá sai số xác lập dựa trên hàm quá độ.
20
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
1
δ
1
0 0
δ
h(t)
h(t)
t t
Đồ án lý thuyết điều khiển tự động
Ta có: E(s)=R(s)-Y(s)
Trường hợp với vòng phản hồi đơn vị làm tương tự ta có:
1.2. Đánh giá chất lượng ở trạng thái quá độ.
+) Đánh giá dựa trên hàm quá độ
21
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
h(t)
Yxl

tqdtmax t
+2%.Yxl
-2%.Yxl
Đồ án lý thuyết điều khiển tự động
Từ sai số cho trước 5%(. Trong đồ án ta chọn sai số
Kẻ hành lang sai số: Y
xl
+ 2%.Y
xl
và Y
xl
- 2%.Y
xl
+) Thời gian quá độ: t
qd
+) Độ quá điều chỉnh(: Đặc trưng cho dao động của hệ
+) Thời gian tăng tốc: là khoảng thời gian từ khi có sự tác động của đầu vào đến khi
tín hiệu đầu ra lần đầu tiên đạt đến 90% giá trị xác lập
Thời gian tăng tốc đặc trưng cho tốc độ đáp ứng của bộ điều khiển
+) Thời gian lên đỉnh(thời gian có độ quá điều chỉnh lớn nhất): t
max
II. Các quy luật điều khiển cơ bản
2.1, Bộ điều khiển P
Có hàm truyền là :
w( )
P
p K=
Trong đó Kp là hệ số khuếch đại của quy luật. Theo tính chất của khâu khuếch đại
(hay khâu tỷ lệ) ta thấy tín hiệu ra của khâu luôn luôn trùng pha với tín hiệu vào. Điều
này nói lên ưu điểm của khâu khuếch đại là có độ tác động nhanh. Vì vậy, trong công

nghiệp, quy luật tỉ lệ làm việc ổn định với mọi đối tượng. Tuy nhiên, nhược điểm cơ bản
22
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đồ án lý thuyết điều khiển tự động
của khâu tỉ lệ là khi sử dụng với các đối tượng tĩnh, hệ thống điều khiển luôn tồn tại sai
lệch tĩnh. Để giảm giá trị sai lệch tĩnh thì phải tăng hệ số khuếch đại nhưng khi đó, tính
dao động của hệ thống sẽ tăng lên và có thể làm hệ thống mất ổn định.
Quy luật tỉ lệ thường được dùng cho những hệ thống cho phép tồn tại sai lệch tĩnh.
K càng lớn thì sai số xac lập càng nhỏ.
Nếu tăng KP thì rõ ràng sai lệch tĩnh giảm nhưng lại có biên độ dao động tăng quá,
khi đó hệ thống sẽ mất tính ổn định vì vậy phải lựa chọn thong số cho phù hợp.
2.2, Bộ điều khiển PI
Để hệ thống vừa có tác động nhanh, vừa triệt tiêu được sai lệch dư, người ta kết hợp
quyluật tỉ lệ với quy luật tích phân để tạo ra quy luật tỉ lệ - tích phân.
Hàm truyền có dạng :
Trong đó: Kp là hệ số khuếch đại
T
I
= K
P
/ K
I
là hằng số thời gian tích phân
Hàm truyền tần số của quy luật PI:
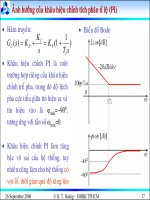
Đồ thị bode
23
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD
Đồ án lý thuyết điều khiển tự động
Đồ thị bode của khâu PI
Về tốc độ tác động thì quy luật PI chậm hơn quy luật tỉ lệ nhưng nhanh hơn quy luật

tích phân.
Trong thực tế, quy luật điều khiển PI được sử dụng khá rộng rãi và đáp ứng được
chất lượng cho hầu hết các quá trình công nghệ. Tuy nhiên, do có thành phần tích phân
nên độ tác động của quy luật bị chậm đi. Vì vậy, nếu đối tượng có nhiễu tác động liên tục
mà hệ thống điều khiển lại đòi hỏi độ chính xác cao thì quy luật PI không đáp ứng được.
2.3, Bộ điều khiển PID
Để tăng tốc độ tác động của quy luật PI, trong thành phần của nó người ta ghép
thêm thành phần vi phân và nhận được quy luật điều khiển tỉ lệ vi tích phân. Có thêm
thành phần vi phân làm tăng tốc độ tác động của hệ thống.
Hàm truyền có dạng :
Trong đó: K
P
là hệ số khuếch đại
T
I
= K
P
/K
I
là hằng số thời gian tích phân
T
D
= K
D
K
P
là hằng số thời gian vi phân
Hàm truyền tần số:
24
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD

Đồ án lý thuyết điều khiển tự động
Về tốc độ tác động, quy luật PID còn có thể nhanh hơn cả quy luật tỉ lệ. Nói tóm lại,
quy luật PID là hoàn hảo nhất. Nó đáp ứng được yêu cầu về chất lượng của hầu hết các
quy trình công nghệ nhưng việc hiệu chỉnh các tham số của nó rất phức tạp, đòi hỏi người
sử dụng phải có một trình độ nhất định. Vì vậy, trong công nghiệp, quy luật PID chỉ sử
dụng ở những nơi cần thiết, khi quy luật PI không đáp ứng được yêu cầu về chất lượng
điều chỉnh.
Đồ thị bode:
Đồ thị bode của khâu PID
Nhận xét: Đây là quy luật điều khiển hoàn hảo nhất, nhanh và chính xác độ sai số
xác lập nhỏ, độ quá điều chỉnh có thể điều chỉnh được. Nhưng lại nhạy cảm với nhiễu và
việc điều chỉnh 3 thông số trên rất phức tạp.
Trên thực tế bộ điều khiển PID có thể được tạo ra từ các mạch các mạch điện, điện
tử… hoặc tạo ra bằng các bộ điều khiển mềm trong máy tính.
Bộ điều khiển PID thường được chế tạo dưới dạng các bộ điều khiển chuyên dụng
và có thể được tích hợp trong các bộ điều khiển khác như PLC, biến tần…
2.4, Mô hình điều khiển
Ta có mô hình khiển với phản hồi âm . Bộ điều khiển PID được ghép nối tiếp với
đối tượng:
25
Sinh viên thực hiện: Nguyễn Đức Hoàng – Đ4.CNTD