Full Giáo Trình Đồ Họa Hướng Dẫn Đầy Đủ

Trường Đại học Khoa học Huế
Khoa CNTT









Giáo trình

Huãú, thaïng 9 nàm 2011


Trang 1
Chương I: Các yếu tố cơ sở của đồ hoạ


I. Các khái niệm cơ bản
I.1. Thiết bị đồ hoạ và điểm ảnh (Pixel)
Các thiết bị đồ hoạ thông dụng như màn hình máy tính, máy in,… cho
phép chúng ta biểu diễn các hình vẽ trên đó. Các thiết bị đồ hoạ này tạo ra mặt
phẳng, đó là một tập hữu hạn các điểm mà mỗi điểm được đánh một cặp chỉ số
nguyên gọi là toạ độ, thông thường mặt phẳng đồ hoạ do thiết bị tạo ra là một
ma trận điểm, mỗi điểm gọi là một Pixel có các thành phần toạ độ là x và y.


Hình I-1. Minh họa việc hiển thị hình ảnh đồ họa trên thiết bị
I.2. Điểm và Đoạn thẳng trong mặt phẳng
Về mặt toán học thì một đoạn thẳng bao gồm một tập vô hạn các điểm trong
mặt phẳng với cặp toạ độ thực. Song do đặc điểm của các thiết bị hiển thị nên
khi biểu diễn trên thiết bị hiển thị của máy tính (như màn hình, máy in,…) thì
được nguyên hoá thành một tập hữu hạn các cặp toạ độ nguyên (Hình I.1).
Chổồng 1: Caùc yóỳu tọỳ cồ sồớ cuớa õọử hoỹa - Nguyóựn Hổợu Taỡi
Trang 2
II. Cỏc thut toỏn v on thng
Phng trỡnh tng quỏt ca mt ng thng c vit di dng:
y=a*x+b
vi

a: l h s gúc hay cũn gi l dc, nú phn ỏnh mi tng quan gia
2 bin s x v y.
b: l khong chn trờn trc honh
Phng trỡnh ng thng i qua 2 im A(x
a
,y
a
) v B(x
b
,y
b
) l:
ab
a
ab
a
xx
xx
yy
yy





(II.a)
(vi x
a
<>x
b

v y
a
<>y
b
.
Khi x
a
=x
b
thỡ phng trỡnh l x=x
a

cũn khi y
a
=y
b
phng trỡnh l y=y
a
)
t
ab
ab
yyy
xxx


thỡ (II.a) tr thnh
aa
yx
x

y
x
x
y
y







baxy
vi









aa
yaxb
x
y
a
(II.b)
II.1. V on thng da vo phng trỡnh

Khi bit c phng trỡnh ca mt ng chỳng ta hon ton cú th v
c ng biu din cho ng ú nh vo cỏc tớnh toỏn trờn phng trỡnh.
õy ng m ta cn biu din l mt on thng AB vi A(x
a
,y
a
) v B(x
b
,y
b
).
Phng trỡnh biu din c cho bi (II.b) vi

baba
yyyxxx ,;,

Quy trỡnh cú th túm tt nh sau:
Nu
xy
: ngha l bin s x bin thiờn nhanh hn bin s y, lỳc ny
m bo tớnh liờn tc ca cỏc im v ta cho bin s x thay i tun t v
tớnh bin s y qua phng trỡnh. C th nh sau:
Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 3
Cho x nhận các giá trị nguyên lần lượt từ x
a
đến x
b
, với mỗi giá trị x ta thực
hiện:

 Tính y=ax+b thông qua phương trình
 Vẽ điểm (x,Round(y)).
Ở đây điểm trên đoạn thẳng có toạ độ là (x,y) song ta không thể vẽ điểm
đó vì giá trị y là một giá trị thực, mà như đã nói ở mục I là các hệ thống
biểu diễn đồ hoạ chỉ có hữu hạn điểm và mỗi điểm có toạ độ nguyên, Vì
thể ta buột phải minh hoạ cho điểm (x,y) trên đường thẳng thực bởi một
điểm trên hệ thống thiết bị đồ hoạ gần với nó nhất đó là điểm có toạ độ
(x,round(y)).

 Ngược lại: nghĩa là biến số y biến thiên nhanh hơn biến số x, lúc này để
đảm bảo tính liên tục của các điểm vẽ ta cho biến số y thay đổi tuần tự và
tính biến số x qua phương trình. Cụ thể như sau:
Cho y nhận các giá trị nguyên lần lượt từ y
a
đến y
b
, với mỗi giá trị y ta thực
hiện:
 Tính x=
a
by 
(hay
aa
xy
y
x
y
y
x
x 







)
 Vẽ điểm (Round(x),y).
 Ví dụ: Cho A(5,4) đến B(10,7) để vẽ đoạn thẳng AB ta thực hiện các bước
sau:
Tính
347
5510


ab
ab
yyy
xxx












1
5
3
aa
yaxb
x
y
a

Vì
xy 
nên ta thực hiện theo cách 1 là cho x nhận các giá trị nguyên lần
lượt từ x
a
đến x
b
, với mỗi giá trị x ta thực hiện:
 Tính y=ax+b thông qua phương trình
 Vẽ điểm (x,Round(y)).
Cụ thể như sau:
Khi x = x
a
= 5: => y = ax+b = 4; Vẽ điểm (5,4)
Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 4
Khi x = 6: => y = 23/5 = 4.6; Vẽ điểm (6,5)
Khi x = 7: => y = 26/5 = 5.2; Vẽ điểm (7,5)
Khi x = 8: => y = 29/5 = 5.8; Vẽ điểm (8,6)
Khi x = 9: => y = 32/5 = 6.4; Vẽ điểm (9,6)
Khi x = 10: => y = 7; Vẽ điểm (10,7)

Kết quả ta có hình vẽ đoạn thẳng AB có thể minh họa như sau:

Hình I-2. Ảnh minh họa một đoạn thẳng từ A(5,4) đến B(10,7)
II.2. Vẽ đoạn thẳng dựa vào thuật toán Bresenham
Từ quy trình vẽ đoạn thẳng trên (II.1) ta thấy đoạn thẳng AB có thể
được vẽ một cách dễ dàng. Song số phép tính cần phải thực hiện trong mỗi
bước vẽ còn lớn, cụ thể là ta còn phải tính 1 phép nhân và 1 phép cộng trên
trường số thực và một phép tính làm tròn (Round). Cũng với tư tưởng như trên
song thuật toán Bresenham hướng tới một sự phân tích bài toán sâu sắc hơn để
tìm ra một quy trình vẽ được các điểm song ít tính toán hơn.
5
6
7
8
9
10
4
5
6
7
Chổồng 1: Caùc yóỳu tọỳ cồ sồớ cuớa õọử hoỹa - Nguyóựn Hổợu Taỡi
Trang 5
Trong phn ny ta ch trỡnh by gii thut trong trng hp h s gúc
ca on thng

1,0a
. Cỏc trng hp cũn li ca h s gúc nh

,1a

;

1,a
;

0,1a
chỳng ta cú th ly i xng on thng qua cỏc ng
phõn giỏc, OX, hay OY quy v trng hp

1,0a
.
Rừ rng l vỡ

1,0a
nờn quy trỡnh õy l cho x nhn cỏc giỏ tr nguyờn ln
lt t x
a
n x
b
, vi mi giỏ tr x ta cn phi tỡm ra mt giỏ tr y nguyờn
(x,y) chớnh l to ca im cn minh ho trờn thit b, song giỏ tr y tỡm ra
õy phi thụng qua ớt phộp tớnh toỏn hn quy trỡnh II.1.
Gi thit vi hai im u mỳt A(x
a
,y
a
) v B(x
b
,y
b

) cú to nguyờn v x
a
<x
b
.
Rừ rng im u tiờn cn biu din trờn thit b ú l im cú to (x
a
,y
a
).
Nu gi im chn c u tiờn l (x
0
,y
0
) thỡ
(x
0
,y
0
)= (x
a
,y
a
)
theo lp lun quy np ta:
Gi thit rng n bc th i ta ó chn c im th i, hay núi cỏch khỏc
l im chn th i l (x
i
,y
i

) ó c xỏc nh giỏ tr.
Vy n bc tip theo (i+1) ta s chn im no? Hay núi cỏch khỏc l
im chn th (i+1) l (x
i+1
,y
i+1
) s cú to bng bao nhiờu.
(Chỳ ý: x
i
,y
i
l tờn gi ca to im chn th i, vớ d nh (x
0
,y
0
) l tờn gi
ca im chn u tiờn (i=0) v nú cú giỏ tr l (x
a
,y
a
))
tr li cõu hi ny ta cn da vo mt s lp lun sau:
Nh trờn ó trỡnh by thỡ im chn th i+1 s phi cú honh x bng honh
ca im trc ú cng thờm 1:
Hay x
i+1
=x
i
+1
Gi M l im thuc AB sao cho x

M
=x
i+1
=x
i
+1
thỡ y
M
= ax
M
+b=a(x
i
+1)+b= (ax
i
+b)+a
vy im tip theo thuc on thng m ta cn tỡm minh ho trờn thit b l
M(x
i
+1, (ax
i
+b)+a). Cõu hi t ra l ta s chn im no trong 2 im
P(x
i
+1,y
i
) v Q(x
i
+1,y
i
+1) minh ho cho M trờn thit b ho.

Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 6

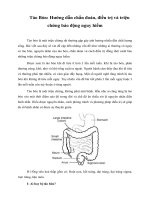
Hình I-3. Minh họa việc chọn lựa điểm P hay Q dựa vào các tham số
Để trả lời câu hỏi này ta đi xét một biểu thức trung gian:
Đặt d
1
=y
M
-y
P
; và d
2
=y
Q
-y
M

Xét biểu thức:
d
1
-d
2
=(y
M
-y
P
)-( y
Q
-y

M
)=2y
M
-(y
P
+y
Q
) =








2
2
QP
M
yy
y

Nếu gọi I là trung điểm của QP thì:
 
IM
yydd  2
21

Rõ ràng là:

 Nếu d
1
-d
2
<0 thì điểm y
M
<y
I
, suy ra P gần điểm M hơn Q, vậy ta sẽ chọn
điểm P là điểm minh họa cho M trên thiết bị đồ hoạ
 Nếu d
1
-d
2
>0 thì điểm y
M
>y
I
, suy ra Q gần điểm M hơn P, vậy ta sẽ chọn
điểm Q là điểm minh họa cho M trên thiết bị đồ hoạ
 Nếu d
1
-d
2
=0 thì điểm y
M
=y
I
, suy ra khả năng lựa chọn P và Q là như nhau,
song ta phải quyết định chọn một điểm. Trong tình huống này ta quyết định

chọn điểm Q.
Vậy để tìm được điểm minh hoạ tiếp theo ta cần xét dấu của biểu thức d
1
-d
2
.
Song ta thấy biểu thức d
1
-d
2
còn khá phức tạp và phải thực hiện tính toán trên
trường số thực do trong đó có xuất hiện phép chia:
y
M
=(ax
i
+b)+a
x
y
yx
x
y
x
x
y
ayaxax
aaiaai









 ))((
(*)
Để tránh tính biểu thức d
1
-d
2
trên trường số thực người ta hướng tới một biểu
thức tương đương về dấu đó là
)(
21
ddxP
i


d
2
d
1
x
i

y
i
+1
y

i

x
i
+1
P
Q
M
I
Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 7
Việc đưa
x
vào nhằm loại bỏ mẫu số trong biểu thức (d
1
-d
2
) để thu được biểu
thức P
i
tính trên trường số nguyên. Thật vậy:
xxyxyP
yyxyyyxyyyxddxP
iMi
iMiiMQPMi


22
)122())1(2())(2()(
21

Thay y
M
bởi giá trị ở (*) ta được:
xyxyyxxyyx
xxyyxyyxyxP
aaii
iaaii


22222
22222
(a)
Ta thấy biểu thức P
i
được xác lập từ toạ độ của điểm chọn thứ i là (x
i
,y
i
).
Vậy P
i+1
sẽ được xác lập từ điểm chọn thứ i+1 là (x
i+1
,y
i+1
) như sau:
xyxyyxxyyxP
aaiii



22222
111
(b)
Vì dấu của P
i
và dấu của (d
1
-d
2
) là tương đương nên có thể tóm tắt quy
tắc chọn điểm tiếp theo như sau:
 Nếu P
i
<0: Thì chọn điểm P làm điểm minh họa cho M trên thiết bị đồ hoạ
Hay nói cách khác là điểm chọn thứ i+1 là (x
i+1
,y
i+1
) sẽ có giá trị bằng P
Nghĩa là: (x
i+1
,y
i+1
)=(x
i
+1,y
i
)
Thay vào (b) ta có:

yP
xyxyyxxyxyP
i
aaiii



2
2222)1(2
1

 Nếu
0
i
P
: Thì chọn điểm Q là điểm minh họa cho M trên thiết bị đồ hoạ
Hay nói cách khác là điểm chọn thứ i+1 là (x
i+1
,y
i+1
) sẽ có giá trị bằng Q
Nghĩa là: (x
i+1
,y
i+1
)=(x
i
+1,y
i

+1)
Thay vào (b) ta có:

xyP
xyxyyxyxxyP
i
aaiii



22
222)1(2)1(2
1

Khi i=0 thì ta có (x
0
,y
0
)=(x
a
,y
a
) thay vào (a) ta có:
xy
xyxyyxxyyxP
aa


2
22222

000

Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 8
Vậy từ đây ta thấy được quy trình chọn ra các điểm trên thiết bị để minh hoạ
cho đoạn thẳng AB theo thuật toán Bresenham như sau:
 Điểm chọn đầu tiên (i=0) là (x
0
,y
0
)=(x
a
,y
a
) và giá trị
xyP  2
0

 Dựa vào giá trị của P
0
là âm hay dương mà ta lại chọn được điểm tiếp theo
(x
1
,y
1
) và tính được giá trị P
1

 Dựa vào giá trị của P
1

là âm hay dương mà ta lại chọn được điểm tiếp theo
(x
2
,y
2
) và tính được giá trị P
2

 Cứ như vậy ta tìm ra được tập các điểm trên thiết bị đồ hoạ để minh hoạ cho
đoạn thẳng AB.
II.2.a. Tóm tắt thuật toán Bresenham:
 Bước 1:
Tính ∆x;∆y
Const1=2∆y; Const2=2∆y-2∆x
P
0
=2∆y-∆x; (x
0
, y
0
) = (x
a
,

y
a
)
Vẽ điểm (x
0
, y

0
)
 Bước 2: Với mỗi giá trị i (i=0,1,2,…) ta xét dấu P
i

 Nếu P
i
<0: thì chọn điểm tiếp theo là
(x
i+1
,y
i+1
)=(x
i
+1,y
i
)
P
i+1
=P
i
+Const1
 Ngược lại (tức Pi ≥ 0): thì chọn điểm tiếp theo là
(x
i+1
,y
i+1
)=(x
i
+1,y

i
+1)
P
i+1
=P
i
+Const2
Vẽ điểm (x
i+1
,y
i+1
) vừa tìm được
 Bước 3: Lặp lại bước 2 với những giá trị i tiếp theo, cho đến khi điểm tìm
được trùng với B, nghĩa là x
i+1
=x
b
thì thuật toán kết thúc.
II.2.b. Ví dụ:
Cho đoạn thẳng AB với A(5,6) và B(10,10). Sử dụng thuật toán Bresenham chúng ta
có thể tìm được các Pixel cần vẽ để biểu diễn đoạn AB trên màn hình như sau:

Bước 1:
∆x = 10-5 = 5; ∆y = 10-6 = 4;
Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 9
Const1 = 2∆y = 8; Const2 = 2∆y-2∆x = 8-10 = -2;
P
0
= 2∆y-∆x = 8-5 = 3; (x

0
, y
0
) = (x
a
,

y
a
) = (5,6)
Vẽ điểm (x
0
, y
0
)
 Bước 2: Bước lặp:
i = 0:
Ta có P
0
= 3≥0 nên:
(x
1
,y
1
) = (x
0
+1,y
0
+1) = (6,7)
P

1
=P
0
+Const2 = 3+(-2)=1
Vẽ điểm (x
1
, y
1
) = (6,7)
i = 1:
Ta có P
1
= 1≥0 nên:
(x
2
,y
2
) = (x
1
+1,y
1
+1) = (7,8)
P
2
=P
1
+Const2 = 1+(-2)= -1
Vẽ điểm (x
2
, y

2
) = (7,8)
i = 2:
Ta có P
2
= -1<0 nên:
(x
3
,y
3
) = (x
2
+1,y
2
) = (8,8)
P
3
=P
2
+Const1 = -1+8 = 7
Vẽ điểm (x
3
, y
3
) = (8,8)
i = 3:
Ta có P
3
= 7≥0 nên:
(x

4
,y
4
) = (x
3
+1,y
3
+1) = (9,9)
P
4
=P
3
+Const2 = 7+(-2) = 5
Vẽ điểm (x
4
, y
4
) = (9,9)
i = 4:
Ta có P
4
= 5≥0 nên:
(x
5
,y
5
) = (x
4
+1,y
4

+1) = (10,10)
P
5
=P
4
+Const2 = 5+(-2) = 3
Vẽ điểm (x
5
, y
5
) = (10,10)
Vì x
5
= x
b
= 10 nên kết thúc vòng lặp và cũng là kết thúc thuật toán.

Hình vẽ minh họa:
Chổồng 1: Caùc yóỳu tọỳ cồ sồớ cuớa õọử hoỹa - Nguyóựn Hổợu Taỡi
Trang 10

Hỡnh I-4. Minh ha on thng c v trờn thit b ha. Cỏc Pixel vuụng mu chớnh l
hỡnh nh th hin ca on thng AB trờn mn hỡnh mỏy tớnh
II.2.c. Hng dn cho cỏc trng hp h s gúc ngoi on [0, 1]
Gi s cho A(0,50), B(100,10) dng on thng AB ta cn tin hnh mt s
phõn tớch:
x = x
b
x
a

= 100 0 = 100
y = y
b
y
a
= 10 50 = -40
Suy ra h s gúc a = y/x = -0.4 [-1,0)
Lỳc ny ta cn ly i xng ca AB qua trc OX c CD vi C(0,-50)
D(100,-10) nờn xột trờn on thng CD ta cú
x = x
d
x
c
= 100 0 = 100
y = y
d
y
c
= -10 (-50) = 40
Suy ra h s gúc a = y/x = 0.4 [1,0] tha món iu kin ca thut toỏn
Bresenham. T ú chỳng ta cú th ỏp dng thut toỏn Bresenham tớnh toỏn
ra cỏc im cn v trờn CD nhng chỳng ta s khụng v nú (vỡ mc ớch chỳng
ta l v AB) m li ly i xng qua trc OX (tc i xng ngc li vi lỳc
5
6
7
8
9
10
6

7
8
9
10
Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 11
đầu) rồi mới vẽ, thì lúc này các điểm vẽ ra sẽ là hình ảnh của đoạn thẳng AB.
Như thế CD chỉ đóng vai trò trung gian để áp dụng được thuật toán còn kết quả
sau cùng ta thu được vẫn là hình ảnh minh họa cho đoạn AB.
Áp dụng tương tự:
+ trường hợp hệ số góc
),1( a
, lúc này chúng ta cần lấy đối xứng qua
đường phân giác của góc phần tư thứ nhất để hệ số góc được quy về [0,1].
+ trường hợp hệ số góc
)1,( a
, lúc này chúng ta cần lấy 2 lần đối xứng.
Đối xứng qua OX rồi tiếp đến đối xứng qua đường phân giác.
Xét điểm M(x,y). Đối xứng qua OX ta được tọa độ mới là (x,-y). tiếp
đến lấy đối xứng qua tia phân giác góc phần tư thứ nhất ta được (-y,x).
II.2.d. Cài đặt thuật toán
 Sinh viên cần xây dựng một thủ tục vẽ đoạn thẳng AB với giả thiết đầu vào
thoả hệ số góc thuộc đoạn [0,1]
 Sinh viên cần xây dựng một thủ tục vẽ đoạn thẳng tổng quát cho phép vẽ
đoạn thẳng AB trong mọi trường hợp, và một chương trình minh hoạ có sử
dụng thủ tục này.

III. Các thuật toán vẽ đường tròn
Phương trình đường tròn tâm O (gốc
toạ độ) bán kính R (nguyên)là:

X
2
+Y
2
=R
2

Trong mục này ta chỉ cần tìm
phương pháp vẽ đường tròn tâm tại
gốc toạ độ. Nếu ta vẽ được đường
tròn tâm tại gốc toạ độ thì bằng cách
thêm vào phép tịnh tiến ta được
đường tròn tâm (x,y) bất kỳ.
Ở đây ta thấy để vẽ được đường
tròn tâm gốc toạ độ ta chỉ cần tìm
phương pháp vẽ cung một phần tám AB, và với các phép lấy đối xứng ta sẽ
có các phần còn lại của đường tròn.
A
B
Chổồng 1: Caùc yóỳu tọỳ cồ sồớ cuớa õọử hoỹa - Nguyóựn Hổợu Taỡi
Trang 12
Vi cung AB thỡ rừ rng dc ca nú thuc on [-1,0]. iu ny ta cú
th d dng thy qua gúc ca tip tuyn vi cung AB hay qua o hm
phng trỡnh biu din cung AB.
Vỡ cung AB cú dc trong khong [-1,0], nờn ta suy ra rng trờn ton
b cung AB khi bin s x tng thỡ bin s y gim, v tc thay i ca y
chm hn ca x. T õy ta cú th ra mt quy trỡnh dng cung AB l:
Cho bin s x nhn ln lt cỏc giỏ tr nguyờn t x
a
n x

b
. Vi mi giỏ tr x
ta thc hin:
Tỡm giỏ tr y nguyờn tng ng im cú to nguyờn (x,y) s l
im gn nht im (x,y
circle
) thuc ng trũn
V im (x,y) tỡm c v cỏc i xng ca nú cú c ng trũn
Trong mc ny ta s i tỡm hiu 2 thut toỏn cho phộp dng ng trũn
(thc cht l dng cung AB v cỏc i xng ca nú) mt cỏch hiu qu v
mt tc .
III.1. Thut toỏn v ng trũn MidPoint
Thut toỏn MidPoint hay cũn gi l thut toỏn xột im gia.
im u tiờn c chn v s l im A(0,R), ngha l: (x
0
,y
0
)=(0,R)
Gi s n bc th i ta ó chn c im (x
i
,y
i
) v. Cõu hi t ra l
n bc th i+1 ta s chn im (x
i+1
,y
i+1
) cú giỏ tr bng bao nhiờu?
Vỡ im tip theo s chn theo quy tc ó núi trờn, nờn cú honh x
tng mt giỏ tr so vi giỏ tr ca im chn trc, hay núi cỏch khỏc l:

x
i+1
=x
i
+1
ng thi vỡ trờn cung AB khi x tng thỡ y gim v tc thay i ca y
chm hn ca x, nờn rừ rng ta thy l vi giỏ tr x tng 1 thỡ giỏ tr y s
gim i mt lng -1y0. M im chn bc trc l (x
i
,y
i
) nờn im
chn tip theo (x
i+1
,y
i+1
) ch cú th l mt trong hai im P(x
i
+1,y
i
) v
Q(x
i
+1,y
i
-1).

x
i

y
i

y
i
-1
x
i
+1
Q
P
I
Cung AB
Chổồng 1: Caùc yóỳu tọỳ cồ sồớ cuớa õọử hoỹa - Nguyóựn Hổợu Taỡi
Trang 13
Hỡnh I-5. Minh ha vic chn la im P hay Q da vo cỏc tham s
quyt nh c im chn l P hay Q chỳng ta hng n mt biu
thc m du ca nú cho phộp chỳng ta ra quyt nh chn im no.
Trc ht chỳng ta xột hm:

222
),( Ryxyxf
circle


Vi mt im M(x,y) thỡ rừ rng ta cú:

circle
(M) = (x,y) = x
2

+ y
2
R
2
<0 khi
v ch khi im M nm trong ng
trũn (tõm O bỏn kớnh R)

circle
(M) = (x,y) = x
2
+ y
2
R
2
>0 khi
v ch khi im M nm ngoi ng
trũn (tõm O bỏn kớnh R)

circle
(M) = (x,y) = x
2
+ y
2
R
2
=0 khi
v ch khi im M nm trờn ng trũn
T kt qu trờn, nu ta gi I l trung im
ca PQ thỡ I(x

i
+1,y
i
-0.5) v:
t P
i
=
circle
(I)=
circle
(x
i
+1,y
i
-0.5)=(x
i
+1)
2
+ (y
i
-0.5)
2
R
2
(a)
Khi P
i
=
circle
(I) <0 thỡ im I nm trong ng trũn (tõm O bỏn kớnh R), vỡ

th im P s gn vi ng trũn hn im Q, do ú ta s chn im P lm
im biu din (v).
Khi P
i
=
circle
(I) >0 thỡ im I nm ngoi ng trũn, vỡ th im Q s gn
vi ng trũn hn im P, do ú ta s chn im Q lm im biu din.
Khi P
i
=
circle
(I) =0 thỡ im I nm trờn ng trũn, suy ra kh nng la
chn P v Q l nh nhau, song ta phi quyt nh chn mt im. Trong
tỡnh hung ny thut toỏn quy nh chn im Q.
Vy t õy ta thy cú th da vo du ca biu thc P
i
ra quyt nh chn
im tip theo.
thut toỏn c n gin ngi ta ti u hoỏ vic tớnh P
i
theo cụng
thc truy hi:
P
i+1
=(x
i+1
+1,y
i+1
-0.5)=(x

i+1
+1)
2
+ (y
i+1
-0.5)
2
R
2
(b)
Du ca P
i
s quyt nh giỏ tr P
i+1
c th nh sau:
Nu P
i
<0: thỡ im chn tip theo l P(x
i
+1,y
i
), ngha l
(x
i+1
,y
i+1
)=(x
i
+1,y
i

).
Thay vo (b) ta c:
P
i+1
=(x
i
+1+1)
2
+ (y
i
-0.5)
2
R
2
= P
i
+ 2(x
i
+1)+1 = P
i
+ 2x
i
+3
M
K
R
<0
>0
Hỡnh I-6. Minh ha hm
circle

f

Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 14
 Nếu P
i
≥0: thì điểm chọn tiếp theo là Q(x
i
+1,y
i
-1), nghĩa là
(x
i+1
,y
i+1
)=(x
i
+1,y
i
-1).
Thay vào (b) ta được:
P
i+1
=(x
i
+1+1)
2
+ (y
i
-1 - 0.5)

2
– R
2
= P
i
+ 2(x
i
+1)+1-2(y
i
-0.5)+1 = P
i
+
2(x
i
–y
i
) +5
Đầu tiên ta chọn điểm A(0,R), nghĩa là (x
0
,y
0
)=(0,R), Thay vào (a) ta có:
RRP 
4
5
4
1
1
0

Vậy quy trình vẽ được thực hiện như sau:
 Tính P
0
, vẽ điểm (x
0
,y
0
)=(0,R)
 Dựa vào dấu của P
0
ta lại chọn được điểm vẽ tiếp theo (x
1
,y
1
) và giá trị P
1

 Dựa vào dấu của P
1
ta lại chọn được điểm vẽ tiếp theo (x
2
,y
2
) và giá trị P
2

 Quá trình trên được lặp đi lặp lại cho đến khi ta vẽ được điểm nguyên gần
nhất với B.
 Một điểm đáng chú ý ở đây các giá trị P tiếp theo có được bằng cách cộng
với giá trị P trước đó với một lượng nguyên 2x

i
+3 hoặc 2(x
i
–y
i
) +5 tuỳ
theo dấu của P. Song nếu giá trị P khởi đầu là
4
1
1
0
 RP
là một giá trị
thực sẽ làm cho việc tính các giá trị P tiếp theo cũng phải xử lý trên trường
số thực. Một điều dễ thấy là nếu ta thay đổi giá trị P
0
khởi đầu là 1-R thì dấu
của P
0
và các P
i
có được sau đó không hề thay đổi về dấu (mặt dù có bị
giảm một lượng 0.25) do đó kết quả thuật toán không hề bị thay đổi, song
các tính toán giá trị P chỉ phải tính trên trường số nguyên.
III.1.a. Tóm tắt thuật toán vẽ đường tròn MidPoint :
 Bước 1: P
0
= 1 – R; (x
0
,y

0
)=(0,R)
Vẽ điểm (x
0
,y
0
)
 Bước 2: Với mỗi giá trị i (i=0,1,2,…) ta xét dấu P
i

 Nếu P
i
<0: thì chọn điểm tiếp theo là
(x
i+1
,y
i+1
)=(x
i
+1,y
i
)
P
i+1
=P
i
+ 2x
i
+3
 Ngược lại (tức P

i
≥ 0): thì chọn điểm tiếp theo là
(x
i+1
,y
i+1
)=(x
i
+1,y
i
-1)
P
i+1
=P
i
+ 2(x
i
- y
i
) +5
Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 15
Vẽ điểm (x
i+1
,y
i+1
) vừa tìm được
 Bước 3: Lặp lại bước 2 với những giá trị i tiếp theo, cho đến khi ta vẽ được
điểm nguyên gần nhất với B, nghĩa là x
i+1

= Trunc(x
b
) =
)
2
(
R
Trunc
thì
thuật toán kết thúc.
III.1.b. Cài đặt
 Sinh viên cần xây dựng một thủ tục vẽ đường tròn theo thuật toán đã trình
bày trên.

Chổồng 1: Caùc yóỳu tọỳ cồ sồớ cuớa õọử hoỹa - Nguyóựn Hổợu Taỡi
Trang 16
Hỡnh I-7. Minh ha vic hin th cỏc im nh ca ng trũn vi cỏc kớch c khỏc nhau
III.2. Thut toỏn v ng trũn Bresenham
Lp lun tng t thut toỏn trờn song khụng dựng hm
circle
m dựng
biu thc (d
1
d
2
). Cú th trỡnh by thut gii nh sau:
im u tiờn c chn v s l im A(0,R), ngha l: (x
0
,y
0

)=(0,R)
Gi s n bc th i ta ó chn c im (x
i
,y
i
) v. Cõu hi t ra l
n bc th i+1 ta s chn im (x
i+1
,y
i+1
) cú giỏ tr bng bao nhiờu?
Vỡ im tip theo s chn theo quy tc ó núi trờn s cú honh x tng
mt giỏ so vi giỏ tr ca im chn trc, hay núi cỏch khỏc l:
x
i+1
=x
i
+1
ng thi vỡ trờn cung AB khi x tng thỡ y gim v tc thay i ca y
chm hn ca x, nờn rừ rng ta thy l vi giỏ tr x tng 1 thỡ giỏ tr y s
gim i mt lng -1y0. M im chn bc trc l (x
i
,y
i
) nờn im
chn tip theo (x
i+1
,y
i+1
) ch cú th l mt trong hai im P(x

i
+1,y
i
) v
Q(x
i
+1,y
i
-1).
quyt nh c im chn l P hay Q chỳng ta hng n mt biu
thc m du ca nú cho phộp chỳng ta ra quyt nh chn im no.
t: d
1
=y
P
2
- y
2
v d
2
=y
2
- y
Q
2


(giỏ tr y õy chớnh l tung ca cung AB ng vi honh x = x
i
+1)

t P
i
= d
1
d
2
= y
P
2
+ y
Q
2
- 2y
2
= y
i
2
+ (y
i
-1)
2
- 2(R
2
- x
i+1
2

)= y
i
2

+
(y
i
-1)
2
- 2(R
2
- (x
i
+1)
2
)
= y
i
2
+ (y
i
-1)
2
- 2R
2
+ 2(x
i
+1)
2
(a)
Du ca biu thc P
i
cho phộp xỏc nh im chn tip theo l P hay Q.
Khi P

i
<0: thỡ im P s gn vi ng trũn hn im Q, do ú ta s chn
im P lm im biu din (v).
Khi P
i
>0: thỡ im Q s gn vi ng trũn hn im P, do ú ta s chn
im Q lm im biu din.
Khi P
i
=0: khong cỏch t P v Q n ng trũn u bng nhau, nờn ta cú
th chn P hay Q u c. Trong tỡnh hung ny thut toỏn quy c chn
im Q lm im biu din.
Vy t õy ta thy cú th da vo du ca biu thc P
i
ra quyt nh chn
im tip theo.
Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 17
Để thuật toán được đơn giản người ta tối ưu hoá việc tính P
i
theo công
thức truy hồi:
P
i+1
= y
i+1
2
+ (y
i+1
-1)

2
- 2R
2
+ 2(x
i+1
+1)
2
(b)
Dấu của P
i
sẽ quyết định giá trị P
i+1
cụ thể như sau:
 Nếu P
i
<0: thì điểm chọn tiếp theo là P(x
i
+1,y
i
), nghĩa là
(x
i+1
,y
i+1
)=(x
i
+1,y
i
).
Thay vào (b) ta được:

P
i+1
= y
i
2
+ (y
i
-1)
2
- 2R
2
+ 2((x
i
+1)+1)
2
= P
i
+ 2(2(x
i
+1)+1) = P
i
+4x
i
+6
 Nếu P
i
≥0: thì điểm chọn tiếp theo là Q(x
i
+1,y
i

-1), nghĩa là
(x
i+1
,y
i+1
)=(x
i
+1,y
i
-1).
Thay vào (b) ta được:
P
i+1
= (y
i
-1)
2
+ (y
i
-2)
2
- 2R
2
+ 2((x
i
+1)+1)
2
= P
i
+( -4y

i
+4) +
2(2(x
i
+1)+1)
= P
i
+ 4(x
i
- y
i
) +10
Đầu tiên ta chọn điểm A(0,R), nghĩa là (x
0
,y
0
)=(0,R), Thay vào (a) ta có:
P
0
= y
0
2
+ (y
0
-1)
2
- 2R
2
+ 2(x
0

+1)
2
= R
2
+ (R-1)
2
-2R
2
+ 2
= R
2
+ R
2
-2R +1 -2R
2
+ 2 = 3 - 2R
Vậy quy trình vẽ được thực hiện như sau:
 Tính P
0
, vẽ điểm (x
0
,y
0
)=(0,R)
 Dựa vào dấu của P
0
ta lại chọn được điểm vẽ tiếp theo (x
1
,y
1

) và giá trị P
1

 Dựa vào dấu của P
1
ta lại chọn được điểm vẽ tiếp theo (x
2
,y
2
) và giá trị P
2

 Quá trình trên được lặp đi lặp lại cho đến khi ta vẽ được điểm nguyên gần
nhất với B.
III.2.a. Tóm tắt thuật toán vẽ đường tròn Bresenham :
 Bước 1: P
0
= 3 - 2R; (x
0
,y
0
)=(0,R)
Vẽ điểm (x
0
,y
0
)
 Bước 2: Với mỗi giá trị i (i=0,1,2,…) ta xét dấu P
i

 Nếu P
i
<0: thì chọn điểm tiếp theo là
Chổồng 1: Caùc yóỳu tọỳ cồ sồớ cuớa õọử hoỹa - Nguyóựn Hổợu Taỡi
Trang 18
(x
i+1
,y
i+1
)=(x
i
+1,y
i
)
P
i+1
=P
i
+ 4x
i
+6
Ngc li (tc P
i
0): thỡ chn im tip theo l
(x
i+1
,y
i+1
)=(x
i

+1,y
i
-1)
P
i+1
=P
i
+ 4(x
i
- y
i
) +10
V im (x
i+1
,y
i+1
) va tỡm c
Bc 3: Lp li bc 2 vi nhng giỏ tr i tip theo, cho n khi ta v c
im nguyờn gn nht vi B, ngha l x
i+1
= Trunc(x
b
) =
)
2
(
R
Trunc
thỡ
thut toỏn kt thỳc.

III.2.b. Ci t
Sinh viờn cn ci t mt th tc v ng trũn theo thut toỏn Bresenham
v chng trỡnh s dng th tc v cỏc ng trũn ngu nhiờn.
IV. Thut toỏn v Ellipse
Phng trỡnh
chớnh tc ca Ellipse cú
dng:
1
2
2
2
2

b
y
a
x

(I)

dng c ellipse rừ
rng l ta ch cn tỡm
cỏch dng cung AB, cũn
cỏc phn cũn li d dng
cú c bng cỏch ly
i xng. Song vi t tng chung dng mt ng bt k l cn phi xỏc
nh ra cỏc min m trờn ton min ú mt bin s bin thiờn nhanh hn mt
bin s khỏc.
Rừ rng trờn cung AB thỡ dc gim liờn tc t im A ( dc bng 0) n
B ( dc tin n -). Xột v tc bin thiờn ca 2 bin s thỡ:

Tc bin thiờn ca bin s X gim dn t A n B.
Tc bin thiờn ca bin s Y tng dn t A n B.
A(0,b)
C(x
0
, y
0
)
B(a,0)
Hỡnh I-8. Hỡnh Ellipse vi cỏc cung AC v BC
Chổồng 1: Caùc yóỳu tọỳ cồ sồớ cuớa õọử hoỹa - Nguyóựn Hổợu Taỡi
Trang 19
Rừ rng trờn cung AB phi cú mt im m ti ú tc bin thiờn ca X v Y
l bng nhau (song x tng thỡ y gim), ú chớnh l im m ti ú cú dc
bng -1.
Gi C(x
0
,y
0
) l im nm trờn cung AB ca ellipse m tip tuyn ti ú cú
dc bng -1. Khi ú tip tuyn d ca ellipse s cú dng:
1
2
0
2
0

b
yy
a

xx

Mt khỏc do dc ca d l:
1
2
0
2
0

ay
bx
nờn ta suy ra
0
2
2
0
x
a
b
y
( õy ta cú x
0
0) =>
2
0
4
4
2
0
x

a
b
y
(a)
mt khỏc do C thuc ellipse nờn ta cú:
1
2
2
0
2
2
0

b
y
a
x
(b)
T (a) v (b) ta suy ra:
22
2
0
ba
a
x


v
22
2

0
ba
b
y



Ta s trỡnh by gi thut v cung AC (i t A n C theo chiu kim ng
h). Cung CB c thc hin mt cỏch tng t khi ta i vai trũ ca x v y.
Cỏc phn cũn li ca ellipse cú c bng cỏch ly i xng.
Trờn cung AC dc nm trong on [0,-1], ngha l x tng thỡ y gim v
tc bin thiờn ca x ln hn ca y. Vy nờn t tng ca thut gii dng
cung AC s l cho tham s x bin thiờn tun t t x
a
n x
c
vi cỏc giỏ tr
nguyờn, v vi mi giỏ tr x nh vy ta tỡm mt giỏ tr y nguyờn gn nht
vi giỏ tr y thc ca ellipse tng ng vi x.
Sau õy chỳng ta s tỡm hiu thut toỏn Bresenham ỏp dng cho dng ellipse.
IV.1. Thut toỏn Bresenham cho v hỡnh Ellipse
Rừ rng im u tiờn c chn v s l im A(0,b), ngha l:
(x
0
,y
0
)=(0,b)
Gi s n bc th i ta ó chn c im (x
i
,y

i
) v. Cõu hi t ra l
n bc th i+1 ta s chn im (x
i+1
,y
i+1
) cú giỏ tr bng bao nhiờu?
Vỡ im tip theo s cú honh x tng mt giỏ tr so vi giỏ tr ca
im chn trc, hay núi cỏch khỏc l:
x
i+1
=x
i
+1
Chổồng 1: Caùc yóỳu tọỳ cồ sồớ cuớa õọử hoỹa - Nguyóựn Hổợu Taỡi
Trang 20
ng thi vỡ trờn cung AC khi x tng thỡ y gim v tc thay i ca y
chm hn ca x, nờn rừ rng ta thy l vi giỏ tr x tng 1 thỡ giỏ tr y s
gim i mt lng -1y0. M im chn bc trc l (x
i
,y
i
) nờn im
chn tip theo (x
i+1
,y
i+1
) ch cú th l mt trong hai im P(x
i
+1,y

i
) v
Q(x
i
+1,y
i
-1).
quyt nh c im chn l P hay Q chỳng ta hng n mt biu
thc m du ca nú cho phộp chỳng ta ra quyt nh chn im no.
t: d
1
=y
P
2
- y
2
v d
2
=y
2
- y
Q
2


(giỏ tr y õy l tung ca cung AC ng vi honh ang xột x
i+1
)
t P
i

= (d
1
d
2
).a
2

= [y
P
2
+ y
Q
2
- 2y
2
]a
2
= [ y
i
2
+ (y
i
-1)
2
- 2(
2
2
1
22
)(

a
xab
i


)]a
2
= [y
i
2

+ (y
i
-1)
2
-
2
222
))1((2
a
xab
i

]a
2

= y
i
2
.a

2
+ (y
i
-1)
2
.a
2
- 2b
2
[a
2
(x
i
+1)
2
]
= y
i
2
.a
2
+ (y
i
-1)
2
.a
2
- 2b
2
a

2
+ 2b
2
(x
i
+1)
2
(a)
(lng a
2
c a vo nhm mc ớch kh mu ca (d
1
-d
2
) song khụng lm
cho P
i
v (d
1
- d
2
) khỏc du )
Du ca biu thc P
i
cho phộp xỏc nh im chn tip theo l P hay Q.
Khi P
i
<0: thỡ im P s sỏt vi cung AC hn im Q, do ú ta s chn im
P lm im biu din (v).
Khi P

i
>0: thỡ im Q s sỏt vi cung AC hn im P, do ú ta s chn im
Q lm im biu din.
Khi P
i
=0: khong cỏch t P v Q n cung AC u bng nhau, nờn ta cú th
chn P hay Q u c. Trong tỡnh hung ny thut toỏn quy c chn
im Q lm im biu din
Vy t õy ta thy cú th da vo du ca biu thc P
i
ra quyt nh chn
im tip theo.
thut toỏn c n gin ngi ta ti u hoỏ vic tớnh P
i
theo cụng
thc truy hi:
P
i+1
= y
i+1
2
.a
2
+ (y
i+1
-1)
2
.a
2
- 2b

2
a
2
+ 2b
2
(x
i+1
+1)
2
(b)
Du ca P
i
s quyt nh giỏ tr P
i+1
c th nh sau:
Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 21
 Nếu P
i
<0: thì điểm chọn tiếp theo là P(x
i
+1,y
i
), nghĩa là
(x
i+1
,y
i+1
)=(x
i

+1,y
i
).
Thay vào (b) ta được:
P
i+1
= y
i
2
.a
2
+ (y
i
-1)
2
.a
2
- 2b
2
a
2
+ 2b
2
[(x
i
+1)+1]
2

= P
i

+2b
2
[2(x
i
+1)+1]
= P
i
+ 2b
2
(2x
i
+ 3)
 Nếu P
i
≥0: thì điểm chọn tiếp theo là Q(x
i
+1,y
i
-1), nghĩa là
(x
i+1
,y
i+1
)=(x
i
+1,y
i
-1).
Thay vào (b) ta được:
P

i+1
= (y
i
-1)
2
.a
2
+ (y
i
-2)
2
.a
2
- 2b
2
a
2
+ 2b
2
[(x
i
+1)+1]
2

= P
i
+ a
2
(-4y
i

+4) + 2b
2
[2(x
i
+1)+1]
= P
i
+ 4a
2
(1-y
i
) + 2b
2
(2x
i
+ 3)
= P
i
+ 2b
2
(2x
i
+ 3) + 4a
2
(1-y
i
)
Đầu tiên ta chọn điểm A(0,b), nghĩa là (x
0
,y

0
)=(0,b), Thay vào (a) ta có:
P
0
= y
0
2
.a
2
+ (y
0
-1)
2
.a
2
- 2b
2
a
2
+ 2b
2
(x
0
+1)
2
=b
2
a
2
+(b-1)

2
a
2
-2a
2
b
2
+ 2b
2

= b
2
a
2
+a
2
b
2
-2a
2
b +a
2
-2a
2
b
2
+2b
2
= -2a
2

b +a
2
+2b
2

= a
2
(1-2b) + 2b
2

Vậy quy trình vẽ được thực hiện như sau:
 Tính P
0
, vẽ điểm (x
0
,y
0
)=(0,b)
 Dựa vào dấu của P
0
ta lại chọn được điểm vẽ tiếp theo (x
1
,y
1
) và giá trị P
1

 Dựa vào dấu của P
1
ta lại chọn được điểm vẽ tiếp theo (x

2
,y
2
) và giá trị P
2

 Quá trình trên được lặp đi lặp lại cho đến khi ta vẽ được điểm nguyên gần
nhất với C.
IV.1.a. Tóm tắt thuật toán Bresenham cho vẽ Ellipse:
 Bước 1: P
0
= a
2
(1-2b) + 2b
2
; (x
0
,y
0
)=(0,b)
Vẽ điểm (x
0
,y
0
)
 Bước 2: Với mỗi giá trị i (i=0,1,2,…) ta xét dấu P
i

Chổồng 1: Caùc yóỳu tọỳ cồ sồớ cuớa õọử hoỹa - Nguyóựn Hổợu Taỡi
Trang 22

Nu P
i
<0: thỡ chn im tip theo l
(x
i+1
,y
i+1
)=(x
i
+1,y
i
)
P
i+1
=P
i
+ 2b
2
(2x
i
+ 3)
Ngc li (tc P
i
0): thỡ chn im tip theo l
(x
i+1
,y
i+1
)=(x
i

+1,y
i
-1)
P
i+1
=P
i
+ 2b
2
(2x
i
+ 3) + 4a
2
(1-y
i
)
V im (x
i+1
,y
i+1
) va tỡm c
Bc 3: Lp li bc 2 vi nhng giỏ tr i tip theo, cho n khi ta v c
im nguyờn gn nht vi C, ngha l x
i+1
= Trunc(x
C
) =
)(
22
2

ba
a
Trunc


thỡ thut toỏn kt thỳc.

Chỳ ý:
Túm tt thut toỏn trờn ch ỏp dng cho on AC. dng on BC ta
cn cú s thay i vai trũ ca ca x v y cng nh a v b. C th
dng c cung BC cn hoỏn i trong ton b thut toỏn: x thnh y v
y ngc li thnh x, a thnh b v b ngc li thnh a.
Vỡ thut toỏn ch v n Trunc(x
c
) nờn nu phn l ca x
c
ln hn 0.5 (vớ
d Trunc(x
c
=7.65)=7). Nu iu ny c thc hin trờn c 2 cung AC
v BC thỡ s dn n hỡnh nh ghộp ni ca 2 cung l cung AB s thiu
1 im ti C. trỏnh trỡnh trng ny thỡ chỳng ta cú th ỏp dng
Trunc() trờn mt cung, cũn cung cũn li ỏp dung Round().
IV.1.b. Ci t thut toỏn Bresenham cho dng Ellipse
Sau õy l mt chng trỡnh vớ d cho thut toỏn. Chng trỡnh ci t th tc
v Ellipse cú tờn l Bre_Ellipse theo thut toỏn trỡnh by trờn, v chng
trỡnh s dng th tc Bre_Ellipse v cỏc hỡnh Ellipse mt cỏch ngu nhiờn.
uses graph,crt;

procedure init;

var
grDriver: Integer;
grMode: Integer;
ErrCode: Integer;
begin
Chæång 1: Caïc yãúu täú cå såí cuía âäö hoüa - Nguyãùn Hæîu Taìi
Trang 23
grDriver := Detect;
InitGraph(grDriver, grMode,' ');
ErrCode := GraphResult;
if ErrCode <> grOk then
begin Writeln('Graphics error:', GraphErrorMsg(ErrCode));readln;halt end;
end;
procedure Bre_Ellipse(xt,yt:Integer;A,B:longint);
var x,y,P,Const1, Const2:longint; color:byte;

Procedure Put(x,y:integer);
begin
putpixel(x+xt,-y+yt,color);
putpixel(x+xt,y+yt,color);
putpixel(-x+xt,-y+yt,color);
putpixel(-x+xt,y+yt,color);
end;
begin
Color:=Getcolor;

{Ve cung AC}
const1:=trunc(sqr(a) / sqrt(sqr(a)+sqr(b)));
x:=0;y:=b;P:=a*a*(1-2*b)-2*b*b;put(x,y);
repeat

if p<0 then
p:=p+2*b*b*(2*x+3)
else
begin
p:=p+2*b*b*(2*x+3)+4*a*a*(1-y);
y:=y-1;
end;
x:=x+1;
put(x,y);
until x=const1;

{Ve cung BC}
{const2:=trunc(sqr(b) / sqrt(sqr(a)+sqr(b)));}
Const2:=Const1+1;

{ Thay vì quá trình lặp được xét trên y, chúng ta có thể làm điều tượng tự bằng
cách xét trên x. Biết rằng trên toàn bộ cung AB thì x sẽ biến thiên từ 0 đến a, mà
trước đó khi dựng cung AC ta đã cho x biến thiên trong đoạn [0, Const1], vậy trên
cung BC x phải biến thiên trong đoạn [Const1+1, a ] thì sẽ đảm bảo hai cung AC
và CB ghép nối liên tục với nhau. }

y:=0;x:=a;P:=b*b*(1-2*a)-2*a*a;put(x,y);
repeat
if p<0 then
p:=p+2*a*a*(2*y+3)
else
begin