Bài giảng Dao động kỹ thuật Bài 1: Dao động tự do không cản

Bài 1: Dao động tự do không cản Kalyrus
MỞ ĐẦU
Nếu một cơ hệ dao động sau khi chịu kích thích ban đầu thì dao động sau
kích thích được gọi là dao động tự do.
Nếu năng lượng dao động không bị mất mát hay tiêu tán do ma sát hay do
các lực cản khác thì dao động được gọi là dao động không cản. Ngược lại, nếu có
bất cứ một phần năng lượng dao động nào bị mất mát do các lực cản thì dao động
được gọi là dao động có cản.
Nội dung của chương I chúng ta chỉ nghiên cứu các hệ dao động một bậc tự
do. Và cụ thể trong bài này sẽ nghiên cứu một số dạng dao động tự do không cản
một bậc tự do quanh vị trí cân bằng tĩnh. Từ một số bài toán mẫu chúng ta rút ra
dạng tổng quát phương trình chuyển động của các hệ dao động tự do không cản
một bậc tự do. Tiếp theo chúng ta đi tìm nghiệm, đánh giá nghiệm. Trong bài cũng
giới thiệu cách xác định tham số độ cứng của hệ dao động.
I. MỘT SỐ HỆ DAO ĐỘNG TỰ DO KHÔNG CẢN
A. CON LẮC LÒ XO
Cơ hệ bao gồm một vật nặng m treo vào một đầu lò xo có hệ số cứng c, đầu còn lại
của lò xo được cố định (hình 1.1). Bỏ qua khối
lượng lò xo, bỏ qua cản ma sát và không khí. Yêu
cầu thiết lập phương trình vi phân dao động của
hệ dao động.
1. Sử dụng phương trình Lagrange
Trước hết ta cần xác định động năng và thế năng
của hệ. Chọn tọa độ suy rộng của hệ là x.
- Động năng của hệ có dạng:
2
1
T ;
2
mx=
&

- Thế năng
Π
của hệ là tổng thế năng của lò xo
và thế năng vật nặng m.
+ Xác định thế năng của lò xo tại vị trí có tọa độ x.
Ta biết rằng tại vị trí cân bằng tĩnh (ứng với x =
0) lò xo biến dạng một lượng
0
x
. Tại vị trí có tọa độ x lò xo biến dạng một lượng là
0
x x+
. Khi đó thế năng của lò xo tại vị trí x là :

2
1 0
1
( )
2
c x x∏ = +
+ Thế năng của vật khối lượng m tại vị trí có tọa độ x là :
2
mgx∏ = −
Ta có :
1 2
∏ = ∏ +∏
Hay
2
0
1

( )
2
c x x mgx∏ = + −
Mà tại vị trí cân bằng (x=0) ta có
2 2
0 0
1 1
2 2
cx mg cx cx= ⇒ ∏ = +
Chương 1: Dao động tuyến tính một bậc tự do
1
c
x
m
Vị trí cân
bằng tĩnh
Hình 1.1
Bài 1: Dao động tự do không cản Kalyrus
Thay vào phương trình Lagrang II:
d T T
dt x x x
∂ ∂ ∂∏
 
− = −
 ÷
∂ ∂
 
&
Hay
( )

0
d
mx cx
dt
− = −
&
Ta được:
0
=+
cxxm

(1.1)
2. Sử dụng định luật II Newton
Tại vị trí có tọa độ x các lực tác dụng lên vật m bao gồm:
Trọng lượng P=mg
Lực đàn hồi P
đh
=c(x
o
+x)
Trong đó: x
o
là độ biến dạng của lò xo tại vị trí cân bằng tĩnh, ta có cx
o
=mg
Viết phương trình định luật II Newton:
ma P P= +
r r
r
đh

Chiếu lên phương Ox:
( )
o
mx mg c x x= − +
&&

Ta được
0
=+
cxxm

(1.1)
B. CON LẮC TOÁN HỌC
Hệ dao động nhỏ quanh vị trí cân bằng tĩnh gồm
một vật nặng có khối lượng m treo vào một đầu sợi
dây, không giãn chiều dài l, đầu còn lại của sợi dây
được cố định. Dây không giãn, khối lượng không
đáng kể (hình 1.2). Yêu cầu thiết lập phương trình vi
phân dao động. Chọn tọa độ suy rộng của hệ là
ϕ
Động năng chất điểm:
2 2 2
1 1
T v
2 2
m ml
ϕ
= =
&
Ở đó v – vận tốc dài của vật m,

v l
ϕ
=
&
Chọn gốc thế năng tại vị trí cân bằng tĩnh
Thế năng của hệ:
( cos )mg l l
ϕ
Π = −
Thay vào phương trình Lagrang II ta được:
2
sin sin 0
g
ml mgl
l
ϕ ϕ ϕ ϕ
= − ⇒ + =
&& &&
Nếu dao động là nhỏ:
sin
ϕ ϕ
≈
,
Phương trình dao động nhỏ của con lắc có
dạng:

0
g
l
ϕ ϕ

+ =
&&
(1.2)
C. DAO ĐỘNG XOẮN
Xét dao động xoắn của một vật nặng. Hệ dao
động gồm một đĩa tròn gắn chặt vào một trục
đàn hồi. Đầu kia của trục đàn hồi ngàm chặt
vào tường cố định.
Cho momen quán tính của vật nặng đối với trục quay là J.
Chương 1: Dao động tuyến tính một bậc tự do
2
P
l
T
ϕ
Vị trí cân
bằng tĩnh
v
Hình 1.2
c
J
ϕ
Vị trí cân
bằng tĩnh
Hình 1.3
Bài 1: Dao động tự do không cản Kalyrus
Độ cứng xoắn của trục đàn hồi là c.
Giả thiết momen quán tính của trục đàn hồi
đối với trục quay nhỏ hơn nhiều so với momen
quán tính của vật nặng đối với trục quay.

Biểu thức động năng và thế năng của hệ
2 2
1 1
;
2 2
T J c
ϕ ϕ
= Π =
&
Thế vào phương trình Lagrang II:
0J c
ϕ ϕ
+ =
&&
(1.3)
II. TÍNH TOÁN DAO ĐỘNG TỰ DO KHÔNG CẢN
A. TÌM NGHIỆM CỦA PTVP DAO ĐỘNG KHÔNG CẢN
Từ các phương trình (1.1) (1.2) và (1.3) ta thấy phương trình dao động tự do
không cản có dạng:
2
0
o
q q
ω
+ =
&&
Với
2
o
c

m
ω
=
với pt (1.1);
2
o
g
l
ω
=
với pt (1.2) hoặc
2
o
c
J
ω
=
với pt (1.3)
Phương trình có nghiệm dạng:
1 2
cos sin
o o
tq C t C
ω ω
= +
(1.4)
Trong đó C
1
, C
2

là các hằng số
C
1
, C
2
được xác định từ các điều kiện đầu (khi t=0), ta có:
Đặt
(0) , (0)
o o
q q q q= =
& &
1 2
;
o
o
o
q
C q C
ω
⇒ = =
&
Đặt
1 2
sin , cosC A C A
α α
= =
Trong đó A và
α
là các hằng số được xác định theo các công thức sau:
2

2 2 2
0
1 2 0
0
q
A C C q
ω
 
= + = +
 ÷
 
&
;
1
2
.
o
o
o
C q
tg
C q
α ω
= =
&
Khi đó PT (1.4) có thể viết dưới dạng:
)sin(
αω
+= tAq
o

(1.6)
Từ (1.6) ta thấy dao động tự do không cản của hệ một bậc tự do được mô tả
bởi hàm điều hòa. Vì vậy dao động tự do không cản còn được gọi là dao động điều
hòa. Dao động điều hòa có các đặc trưng sau:
A- Biên độ dao động;
o
ω
- Tần số riêng;
αω
+t
o
- Pha dao động;
α
- Pha ban đầu;
o
T
ω
π
2
=
- Chu kỳ dao động.
B. NHẬN XÉT
Chương 1: Dao động tuyến tính một bậc tự do
3
Bài 1: Dao động tự do không cản Kalyrus
Dao động điều hòa có các tính chất sau:
- Tần số riêng và chu kỳ dao động không phụ thuộc vào các điều kiện đầu
mà chỉ phụ thuộc vào các tham số của hệ.
- Biên độ dao động là hằng số. Biên độ dao động và pha ban đầu phụ thuộc
vào điều kiện đầu và các tham số của hệ.

Việc xác định tần số dao động riêng
m
c
=
2
0
ω
là nhiệm vụ quan trọng nhất của
bài toán dao động tự do. Bảng (2.1) sách giáo trình thống kê một số công thức tính
tần số riêng của một số hệ dao động đơn giản.
C. VÍ DỤ
Tay biên khối lượng m, dài l.
Tìm tọa độ trọng tâm và mô men quán tính của tay biên đối với trục qua
trọng tâm và vuông góc với mặt phẳng tay biên. Các kích thước cho trên hình vẽ
Bài giải :
Gọi vị trí của trọng tâm là C
Ta làm 2 thí nghiệm xem tay biên là con lắc vật lí, lần lượt có các điểm treo
là A, B. Khoảng cách từ trục quay A tới C là a, khoảng cách từ trục quay B tới C là
b. Theo yêu cầu bài toán ta cần xác định a ( hoặc b) và J
C
.
Viết PT dao động nhỏ quanh A :
0=+
AAA
mgaJ
ϕϕ

mga
J
T

A
A
A
π
ω
π
2
2
==⇒
;
J
A
-Momen quán tính của tay biên đối với trục đi qua A.
Tương tự :
mgb
J
T
B
B
B
π
ω
π
2
2
==
;
J
B
-Momen quán tính của tay biên đối với trục đi qua B.

T
A
, T
B
được xác định bằng thực nghiệm.
Mặt khác ta có 3 PT :
a+b=l ;
J
A
=J
C
+ma
2
; (định lý chuyển trục Huyghen)
J
B
=J
C
+mb
2
.
Như vậy có 5 phương trình, 5 ẩn là J
A
, J
B
, J
C
, a, b
Giải ra ta được :
( )

;
8
4
.
222
22
lTTg
lgT
lb
BA
A
π
π
−+
−
=

2
2
2
4
. mb
T
mgbJ
B
C
−=
π
.
III. XÁC ĐỊNH THAM SỐ ĐỘ CỨNG CỦA CÁC HỆ DAO ĐỘNG

Chương 1: Dao động tuyến tính một bậc tự do
4
B
A
a
b
lC
m
Bài 1: Dao động tự do không cản Kalyrus
Các phần tử đàn hồi trong các hệ dao động hữu hạn bậc tự do thường được
giả thiết bỏ qua khối lượng. Đại lượng đặc trưng cho phẩn tử đàn hồi tuyến tính có
độ cứng và kí hiệu là c. Thứ nguyên của độ cứng c nói chung là khác nhau.
Dưới đây trình bày một số công thức tính toán hệ số cứng c qui đổi.
A. ĐỘ CỨNG QUI ĐỔI CỦA THANH ĐÀN HỒI
1. Xét trường hợp thanh đàn hồi (lò xo) chịu kéo nén.
Từ giáo trình SBVL :
EA
Fl
l =∆
Trong đó : E là mô đun đàn hồi
A là diện tích mặt cắt ngang
lcl
l
EA
F ∆=∆=⇒
Vậy độ cứng qui đổi được xác định bởi công thức:
l
EA
c =
2. Trong trường hợp thanh đàn hồi (lò xo) chịu xoắn.

Từ giáo trình SBVL:
P
x
GI
lM
=∆
ϕ
Trong đó:
G-Modun trượt
I
P
-Momen quán tính cực mặt cắt ngang.
ϕϕ
∆=∆=⇒ c
l
GI
M
P
x
Vậy độ cứng qui đổi trong trường hợp thanh
xoắn có dạng:
l
GI
c
P
=
3. Trường hợp thanh đàn hồi (lò xo) bị uốn.
Xét dầm chịu lực như hình vẽ
Giáo trình SBVL:
EI

Fl
f
3
3
1
=
EI- độ cứng chống uốn;
cff
l
EI
F ==⇒
3
3
Vậy độ cứng qui đổi c được xác định bởi công thức:
3
3
l
EI
c =
Chương 1: Dao động tuyến tính một bậc tự do
5
l
F
l∆
M
x
l
l
F
f

Bài 1: Dao động tự do không cản Kalyrus
B. TÍNH TOÁN LÒ XO TƯƠNG ĐƯƠNG CỦA CÁC HỆ CÁC LÒ XO
1. Đối với hệ có hai lò xo mắc song song
Ta có công thức tính hệ số cứng lò xo
tương đương:
F=c
1
x+c
2
x=c
*
x
21
*
ccc +=⇒
Tổng quát: hệ có n lò xo mắc song song
∑
=
=
n
j
j
cc
1
*
.
2. Đối với hệ có hai lò xo mắc nối tiếp
Ta có : F=c
1
x

1
+c
2
x
2
, x=x
1
+x
2
⇒
F=c
*
x
.
111
21
**
21
cccc
F
c
F
c
F
x +=⇒=+=⇒
Tổng quát: hệ có n lò xo mắc nối tiếp
∑
=
=
n

i
i
cc
1
*
11
.
Chương 1: Dao động tuyến tính một bậc tự do
6
C
2
x
C
1
C
*
C
2
C
1
x
C
*
Bài 1: Dao động tự do không cản Kalyrus
KẾT LUẬN
Đây là bài đầu tiên của chương I về dao động tự do không cản một bậc tự do.
Học viên đã được nghiên cứu các ví dụ cụ thể, sau đó rút ra dạng tổng quát phương
trình dao động của hệ dao động tự do không cản một bậc tự do. Tiếp đó học viên
tiến hành nghiên cứu, giải phương trình vi phân chuyển động và tìm ra nghiệm là
qui luật chuyển động của phần tử dao động. Bài học cũng giới thiệu cách xác định

tham số độ cứng của hệ dao động.
Nội dung của bài học giới thiệu trường hợp hệ dao động đơn giản nhất. Là cơ
sở để học viên tiếp tục nghiên cứu các trường hợp phức tạp hơn trong các bài sau.
Do đó ở bài này học viên cần nắm chắc phương pháp thành lập phương trình vi
phân dao động, áp dụng kiến thức toán học để giải phương trình.
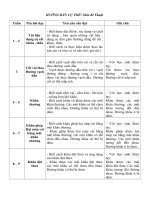
HƯỚNG DẪN NGHIÊN CỨU
Để thuận tiện cho việc tự nghiên cứu và học tập tại đơn vị các học viên cần
thực hiện các nội dung sau:
A. Nắm chắc trọng tâm của bài mục II.A, III.B. Nghiên cứu các phương pháp,
các bước xây dựng phương trình vi phân ở mục I.
- Nghiên cứu sách giáo trình “Dao động kỹ thuật” – Nguyễn Văn Khang
trang [34-43];
- Tự lập phương trình và xác định tần số dao động cho các hệ dao động đơn
giản trong bảng 2.1 trang [39-40] sách giáo trình;
- Nghiên cứu thí dụ 1.5, 1.6 và làm các bài tập 1.1.5, 1.1.6, 1.1.12, 1.1.13
sách bài tập.
Ngày tháng năm 2015
NGƯỜI BIÊN SOẠN
Kalyrus
Chương 1: Dao động tuyến tính một bậc tự do
7