Đề thi thử tốt nghiệp quốc gia môn toán trường trần phú 2016

ĐÁP ÁN – ĐỀ THỬ TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2016 MÔN TOÁN
CÂU

ĐÁP ÁN
4

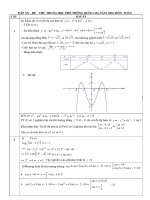
a)) Khảo sát và vẽ đồ thị của hàm số y = - x + 4 x 2 - 3 (1).
· TXĐ D = ¡
1

x = 0
· Sự biến thiên y ' = - 4 x3 + 8 x ; y ' = 0 ⇔ −4 x3 + 8 x = 0 ⇔ 
x = ± 2

(

)

(

)

(

)

Các khoảng đồng biến −∞; − 2 và 0; 2 ; các khoảng nghịch biến − 2;0 và

(

2; +∞

)

- Cực trị: Hàm đạt cực tiểu tại x = 0 , yCT = -3; đạt cực đại tại x = ± 2 , yCĐ = 1
- Giới hạn tại vô cực: lim y = lim y = −∞
x→−∞

· Bảng biến thiên

•

x→+∞

Đồ thị:

2

1

-2

O

-1

1

2

-2

-3
-4

b)Ta có x 4 - 4 x 2 + m - 1 = 0 Û - x 4 + 4 x 2 - 3 = m - 4 (1)
PT (1) có 2 nghiệm khi chỉ khi đường thẳng y = m - 4 cắt với đồ thị hàm số y = - x 4 + 4 x 2 - 3 tại 2
m − 4 = 1
m = 5
⇔
điểm phân biệt. Từ đồ thi trên ta có Pt(1) có 2 nghiệm khi chỉ khi: 
m
−
4
<
−
3

m < 1
Vậy m cần tìm là là m < 1 và m = 5 .
2

a)

(

Ta có

)

log4 16 − 3.2 x = x − 1

⇔ 16 − 3.2 x = 4 x −1 ⇔ 4 x + 12.2 x − 64 = 0

(

)(

)

⇔ 2 x + 16 2 x − 4 = 0 (vì 2 x + 16 > 0 )
⇔ 2 x = 4 ⇔ x = 2 . Vậy nghiệm của phương trình là x = 2 .
 cos x = 0
b) Phương trình đã cho tương đương với 2 cos x ( cos 2 x + 5sin x − 3 ) = 0 ⇔ 
 cos 2 x + 5sin x − 3 = 0
π
• cos x = 0 ⇔ x = + kπ , k ∈ Z
2


sin x = 2 ( vn )
• cos 2 x + 5sin x − 3 = 0 ⇔ −2sin x + 5sin x − 2 = 0 ⇔ 
(1)
sin x = 1

2

π
 x = 6 + k 2π
1
*sin x = ⇔ 
2

 x = 5π + k 2π

6
π
π
5π
Vậy các nghiệm phương trình là x = + k2π ; x = + kπ ; x =
+ k 2π , k ∈ Z .
6
2
6
16
−4
a) Do −π < α < 0 ⇒ sin α < 0 mà sin 2 α = 1 − cos2 α =
nên sin α =
.
25
5
−24
−7
−17
Ta có sin 2α = 2 sin α .cos α =
; cos 2α = 2 cos2 α − 1 =
.
Do đó A =
.
25
25
25
b) Điều kiện n ≥ 2, n ∈ ¥

2

3

Ta có 4Cn2 − 3n = 12 ⇔ 2n2 − 5n − 12 = 0 ⇔ ( n − 4 ) ( 2 n + 3 ) = 0 ⇔ n = 4
3n

12

k

( )

12
12
12−k  2 y 
k 36−4 k k

 3 2y 
2y 
k
3
k
Khi đó  x 3 −
=
x
−
=
C
x

−
=
C
−
2
x
y
(
)
∑
∑
÷

÷

÷
12
12
x
x
x






k =0
k =0
Số hạng thỏa mãn bài toán ứng với 36 − 4k + k = 15 ⇔ k = 7 (nhận)

7

7
Do đó số hạng cần tìm là C12
( −2 ) x 8 y 7 = −101376 x 8 y 7 .

4

Hàm số xác định và liên tục trên đoạn 3;15 ; y ' ( x ) =
1

1

1
2 x +1 x − 2
−

1
= 0 ⇔ x − 2 = 2 x + 1 ⇔ x 2 − 8x = 0 ⇔ x = 8
2 x +1 x − 2
Ta có y ( 3) = 2 , y ( 8) = 3 − ln 6 ; y ( 15 ) = 4 − ln13

Với x ∈  3;18 , y ' ( x ) = 0 ⇔

5

−

Giá trị lớn nhất và giá trị nhỏ nhất của y ( x ) trên đoạn 3;15 lần lượt là 2 và 3 − ln 6 .

y = −∞  lim y = +∞ ÷ ⇒ x = 3 là tiệm cận đứng
a) TXĐ D = ¡ \ { 3} ; xlim
→ 3+
 x → 3−

lim y = lim y = m ⇒ y = m là tiệm cận ngang. Suy ra giao điểm 2 đường tiệm cận là I ( 3; m )
x →−∞

x →+∞

Yêu cầu thỏa mãn khi:

m −1

 m = −1
. Vậy m = −1 và m = 3 .
= 2 ⇔ m −1 = 2 ⇔ 
m = 3
2

10
b) Số phần tử của không gian mẫu là n ( Ω ) = C30
.

Gọi A biến cố “Chọn được 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong đó có đúng 1

5
4
.C31.C12
tấm thẻ mang số chia hết cho 10”. Ta có n ( A ) = C15

.

n ( A ) C155 .C31.C124
99
=
=
Vậy xác suất cần tìm là P ( A) =
10
n ( Ω)
C30
667


Gọi H , N lần lượt trung điểm cạnh BC và AB .
Ta có B ' H ⊥ ( ABC ) và NH ⊥ AB . Suy ra góc giữa
¼' NH = 600 .
hai mặt phẳng ( ABB ' A ' ) và mặt phẳng ( ABC ) là B
Tam giác ABC vuông tại A ,
6

có AC = BC 2 − AB 2 = 4a ⇒ NH = 2a
Tam giác B ' NH vuông tại H ,
¼' NH =
có tan B

B'H
= 3 ⇒ B ' H = 2a 3
HN

Thể tích khối lăng trụ ABC. A ' B ' C ' là V = B ' H .S ABC = 2a 3.

3a.4a
= 12a3 3
2

Gọi E = B ' H ∩ CC ' , M trung điểm AC . Gọi F hình chiếu vuông góc của H trên ME

(

)

Ta có AC ⊥ MH , AC ⊥ B ' H ⇒ AC ⊥ HF ⇒ HF ⊥ ( ACC ' A ' ) ⇒ d H ; ( ACC ' A ' ) = HF
Mặt khác HM =

1
3a
, HE = B ' H = 2a 3
AB =
2
2

Trong tam giác vuông MHE tại H , có đường cao HF , nên
MH .HF

HF =

(

)

HM 2 + HE 2

(

=

)

3
2a 3. a
2

( 2a 3 )

Do, d B '; ( ACC ' A ' ) = d H ; ( ACC ' A ' ) = 2HF =

7

2

2

3 
+  a÷
2 

=

6.a
19

=

6 19a
.
19

12a 19
12a 19
.Vậy d B '; ( ACC ' A ' ) =
19
19

(

)

Gọi H trung điểm DI và K giao điểm của EI và BC
Ta có EH ⊥ DI , góc ∠DBC = ∠DAC (Tính chất thang cân)
và ∠DAC = ∠IEH (góc ở tâm), suy ra ∠DBC = ∠IEH
mà ∠EIH = ∠BIK (đối đỉnh). Do đó ∠ BKI = 900 ⇒ EK ⊥ BC
uur  35 25 
Ta có EI  ; ÷ ,
 8 8 
đường thẳng BC có phương trình là 7 x + 5 y − 33 = 0
uur
Ta có AI = ( −1;3) , đường thẳng AC có phương trình là 3 x + y − 5 = 0
 7 x + 5 y − 33 = 0  x = −1
⇔
⇒ C ( −1;8 )

Tọa độ điểm C là nghiệm của hệ phương trình 
3x + y − 5 = 0
y = 8
 33 − 5b 
; b ÷, b ∈ ¢ . Ta có IA = IB = 10
Điểm B ∈ BC ⇒ B 
 7

b = 1( tm )
2
2
 33 − 5b 

2
Suy ra B ( 4;1)
⇔ 10 = 
− 1÷ + ( b − 2 ) ⇔ 37b − 228b + 191 = 0 ⇔ 
191
b
=
l
7
( )



37
uuur uur 1 − xD = 6
 x = −5
⇔ D

Ta có IC = ID = 2 10 ⇒ DI = 2 IB ⇒ 
. Suy ra D ( −5; 4 ) .
 2 − y D = −2
 yD = 4


(

)

(

3

)

Phương trình tương đương x 2 + 2 x − 1 + 2 x 2 + 2 x − 1 = x 2 − x 4 + 2 3 x 2 − x 4
8
(1,0đ
)

Xét hàm số f ( t ) = t 3 + 2t , t ∈ ¡

(1)

Ta có f ' ( t ) = 3t 2 + 2 > 0 ∀t ∈ ¡ suy ra hàm số f ( t ) liên tục và đồng biến trên ¡

(

)

3 2
3 2
2
4
2
4
Phương trình (1) có dạng f x + 2 x − 1 = f  x − x ÷ ⇔ x + 2 x − 1 = x − x


Với x = 0 thay vào (2) không thỏa mãn

Với x ≠ 0 thì phương trình (2) ⇔ x −

(

1
1
+ 2 = 3 − x . Đặt
x
x

3

(2)

1
− x = t , ta có phương trình
x
2

)

t 3 + t − 2 = 0 ⇔ ( t − 1) t 2 + t + 2 = 0 ⇔ t = 1 ( Vì t 2 + t + 2 =  t + 1 ÷ + 7 > 0 )
 2 4
Với t = 1 ⇔ 3

1
1
−1 ± 5
.
− x = 1 ⇔ − x = 1 ⇔ x2 + x − 1 = 0 ⇔ x =
x
x
2

Vậy nghiệm của phương trình là x =

−1 − 5
−1 + 5
và x =
.
2
2

Theo giả thiết ta có
2
5 ( 4 x 2 + y 2 + z 2 ) = 18 ( xy + yz + zx ) ⇔ 5 ( 2 x + y + z ) = 18 ( xy + yz + zx ) + 10 ( 2 xy + yz + 2 zx )
⇔ 5 ( 2 x + y + z ) = 38 x ( y + z ) + 28 yz ≤ 38 x ( y + z ) + 7 ( y + z )
2

9

2

2

 2x

38 x
x
⇔ 5
+ 1÷ ≤
+7 ⇔
≤1⇔ x ≤ y + z
y+z
y+z
 y+z 
1
2
2
2
2
2
2
Mặt khác ta có ( y + z ) ≤ 2 ( y + z ) ⇔ y + z ≥ ( y + z )
2
y+z
2
2

2
P≤
−
=
−
3
3
1
2
Vì vậy
( y + z ) ( 2 ( y + z ) + y + z ) y + z 27 ( y + z )
2
t = 0
2
2
−2 2
2
4
f ' ( t ) = 2 + 4 f ' ( t ) = 0 ⇒ t = 9t ⇒ 
Đặt t = y + z > 0 . Khi đó P ≤ f ( t ) = −
3
t = ± 1
t 27t
t
9t
3

Bảng biến thiên
1


 x = 3
Vậy max P = 4 khi 
.
y = z = 1

6
-----------HẾT-----------