hd bai tap mat cau

O

Ta phải chứng minh
các góc nào vuông?
D
A
B
C
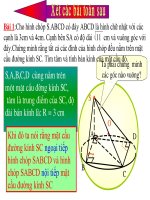
S,A,B,C,D cùng nằm trên một
mặt cầu đường kính SC,
tâm là trung điểm của SC, độ
dài bán kính là: R = 3 cm

Khi ú ta núi rng mt cu
ng kớnh SC ngoi tip
hỡnh chúp SABCD v hỡnh
chúp SABCD ni tip mt
cu ng kớnh SC
S
Bi 1:Cho hỡnh chúp S.ABCD cú ỏy ABCD l hỡnh ch nht vi cỏc
cnh l 3cm v 4cm. Cnh bờn SA cú di 11 cm v vuụng gúc vi
ỏy.Chng minh rng tt c cỏc nh ca hỡnh chúp u nm trờn mt cu
ng kớnh SC. Tỡm tõm v tớnh bỏn kớnh ca mt cu ú.

A
B
C
A
B
C

D
O
D
Bài 2 : CMR tất cả các đỉnh của một hình hộp chữ nhật đều nằm trên
một mặt cầu.
Khi ú ta núi
mt cu tõm O
ngoi tip hỡnh
hp ch nht
hay hỡnh hp
ni tip mt
cu

Quy trình tìm
tâm và bán kính của mặt cầu ngoại tiếp hình chóp
B1. Kiểm tra: Đáy của hình chóp phải có đường tròn ngoại tiếp .
B2. Tìm tâm đường tròn ngoại tiếp đáy
hình chóp.
B3. Dựng trục đường tròn ngoại tiếp
đáy hình chóp,gọi là d.
B4. Dựng mặt phẳng trung trực của một
cạnh bên gọi là mặt phẳng ()
Suy ra O = d()
Phương pháp cơ bản:
D
A
B
C
S

H
O

M

Quy trình tìm
tâm và bán kính của mặt cầu ngoại tiếp hình chóp
Nhưng thông thường:
* Chọn một mặt phẳng (P) thuận lợi sao cho
thoả mãn đồng thời chứa trục đường tròn d.
chứa một cạnh bên SA.
* Trong (P) dựng một đường trung
trực của SA và cắt d tại O, khi đó O
chính là tâm mặt cầu ngoại tiếp hình
chóp đã cho.
D
A
B
C
S

H
O

M

D
A
B
C

S

H
O

M
Đặc biệt:
* Nếu tất cả các đỉnh của hình chóp nhìn một đoạn thẳng cố định dưới
một góc vuông thì hình chóp nội tiếp mặt cầu với tâm nằm trên đoạn
thẳng và đoạn thẳng đó chính là đường kính.
Hoặc:
Nếu có một mặt phẳng (P) chứa
d: Trục đường tròn đáy
: Trục đường tròn của một mặt bên
Thì tâm mặt cầu ngoại tiếp là
O = d .
Quy trình tìm
tâm và bán kính của mặt cầu ngoại tiếp hình chóp