Đề thi thử THPT Quốc gia năm 2017 môn Toán trắc nghiệm - Đề số 4

ĐỀ THAM KHẢO
KỲ THI THPT QUỐC GIA NĂM 2017
Lê Phúc Lữ giới thiệu
(các câu hỏi dưới đây mang tính chất tham khảo để rèn luyện thêm, có thể số lượng câu khó dễ
không giống với đề minh họa của Bộ GD-ĐT)
Bài 1. Một hàm số f (x ) có đạo hàm là f (x )  x (x  1)2 (x  2)3 (x  3)5 . Hỏi hàm số này có bao
nhiêu cực trị?
A. 4

B. 3

C. 2

D. 1

Bài 2. Hàm số nào sau đây đồng biến trên  ?
A. y 

x 1
x 2

B. y 

C. y  x 4  4x  2

1 3 1 2
x  x x
3
2

D. y  x 3  3x 2  3x  1

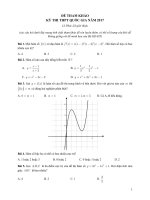
Bài 3. Gọi y  f (x ) là hàm số của đồ thị trong hình vẽ bên dưới. Hỏi với giá trị nào của m thì

f (x )  m có đúng hai nghiệm phân biệt?

A. 0  m  1

B. m  5

C. m  1, m  5

D. Cả A, B đều đúng.

Bài 4. Hàm số bậc ba có thể có bao nhiêu cực trị?
A. 1 hoặc 2 hoặc 3

B. 0 hoặc 2

C. 0 hoặc 1 hoặc 2

D. 2

Bài 5. Gọi A, B,C là ba điểm cực trị của đồ thị hàm số y  2x 4  4x 2  1 . Hỏi diện tích tam
giác ABC là bao nhiêu?
A. 4

B. 2

C. 1

D.

3
2
1


Bài 6. Biết rằng hàm số y 
giá trị của tổng a  b.
A. 5

ax  1
có tiệm cận đứng là x  2 và tiệm cận ngang là y  3 . Tính
bx  2

C. 0

B. 4

D. 1

Bài 7. Cho hàm số y  3 sin x  4 cos x  2 với x  [0;2 ]. Gọi a,b giá trị lớn nhất và nhỏ nhất
của hàm số. Khi đó, tổng a  b bằng bao nhiêu?
A. 10

B. 7

C. 3

D. 9

Bài 8. Hàm số f (x )  x 3  ax  b với a, b   có hai cực trị là x 1, x 2 . Hỏi kết luận nào sau đây
là đúng về hàm này?

 

A. Phương trình f x  m có thể có nghiệm duy nhất.
B. Đồ thị hàm số đi qua gốc tọa độ.
C. Tổng hai giá trị cực trị là b.
D. Hai điểm cực trị của đồ thị hàm số nằm về hai phía của trục tung.
Bài 9. Tiếp tuyến tại điểm cực trị của đồ thị hàm số y  ax 4  bx 2  c, a  0 có gì đặc biệt?
A. Song song với trục tung.

B. Có hệ số góc dương.

C. Song song với trục hoành.

D. Luôn đi qua gốc tọa độ.

Bài 10. Có hai cây cột dựng trên mặt đất lần lượt cao 1m và 4m, đỉnh của hai cây cột cách nhau
5m. Người ta cần chọn một vị trí trên mặt đất (nằm giữa hai chân cột) để giăng dây nối đến hai
đỉnh cột để trang trí như mô hình bên dưới. Tính độ dài dây ngắn nhất.
A.

41

B.

37

C.

29

D. 3 5

B
5
4

A
1

D

x

E

C

 
m  sin x
Bài 11*. Tìm m để hàm số sau nghịch biến trên 0;  : y 
.
cos2 x
 6 
A. m  1

B. m  0

C. m 

5
4

D. m  2
2


Bài 12. Tính đạo hàm của hàm số y  ln(sin x ) .
A. tan x

C.  tan x

B. cotx

D.

1
sin x

Bài 13. Phương trình 22  4 có nghiệm là bao nhiêu?
x

A. 1

B. 0

C. 2

D. 4

Bài 14. Với a,b  0 và a  1,b  1 . Điều kiện nào sau đây cho biết loga b  0 ?
A. (a  1)(b  1)  0

B. ab  1

C. b  1

D. ab  1 .

Bài 15. Tập xác định của hàm số y  (4  x 2 )5 là gì?
A. D  

B. D   \ {2}

Bài 16. Bất phương trình log 4 x  
A. x 

1
2

C. D  (2;2)

D. D  [2;2] .

1
có nghiệm là gì?
2

C. 0  x 

B. x  2

1
2

D. Vô nghiệm.

Bài 17. Với a, b, c  0 và a  1,b  1, c  1 . Biểu thức nào sau đây bằng với a
A. b

loga c

B. c

logb a

C. a logb c

D. c

loga b

logb c

?

.

Bài 18. Hỏi với giá trị a nào thì hàm số y  (3  a )x nghịch biến trên  ?
A. 2  a  3

B. 0  a  1

Bài 19. Cho y  x

2

C. a  2

D. a  0

 3x , tính đạo hàm của y.

A.

2 x

2 1

 3x

B. x

C.

2 x

2 1

 3x ln 3

D.

2

ln x  x  3x 1
1

1 2
x  3x ln 3 .
2

Bài 20*. Người ta thả một lá bèo vào một hồ nước. Kinh nghiệm cho thấy sau 9 giờ, bèo sẽ sinh
sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng lá bèo tăng gấp 10 lần lượng lá bèo trước đó và tốc
1
độ tăng không đổi. Hỏi sau mấy giờ thì số lá bèo phủ kín cái hồ?
3
A. 3

B.

109
3

C. 9  log 3

D.

9
log 3

3


Bài 21. Cho a,b, c thỏa mãn điều kiện a log3 7  27, b
thức T  a

log3 7 

2

b

A. 76  11

log7 11

2

c

log11 25

2

log 7 11

 49, c

log11 25

 11 . Tính giá trị của biểu

.

B. 3141

C. 21

D. 469

Bài 22. Cho f (x ), g(x ) là các hàm số xác định, liên tục trên  . Hỏi khẳng định nào sau đây sai?
A.

  f (x )  g(x )dx   f (x )dx   g(x )dx

B.

 f (x )g(x )dx   f (x )dx  g(x )dx

C.

  f (x )  g(x )dx   f (x )dx   g(x )dx

D.

 2 f (x )dx  2 f (x )dx .

Bài 23. Tính tích phân I 
A.

1
2



1
0

2xdx
.
x2  1

B. ln 2

C. 1

D.

ln 2
2

Bài 24. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y  x 2  4 , trục hoành và hai đường
thẳng x  1, x  1.
A.

406

15

B.

22
3

C.

22
3

D.

11
3

Bài 25. Cho hình H giới hạn bởi đồ thị (C ) : y  (2x  1) ln x , trục hoành, và đường thẳng

x  2 . Tính thể tích khối tròn xoay được tạo thành khi quay H quanh trục hoành.
A.

3

2

5
B.    ln 64
2

C. (ln 64  4)

Bài 26. Nguyên hàm của hàm số y  sin2 x là?

D.

143
9

2x  sin 2x
C
4

A. cos2 x  C

B.

C. x  cos 2x  C

D. 

1
C
cot2 x

Bài 27. Cho bài toán sau: Tìm số a  0 để có đẳng thức



a

0

x 3

x  3  9x

dx 



a

0

9 x

x  3  9x

dx .

Một học sinh giải theo các bước sau đây, hỏi học sinh đó đã giải sai ở bước nào?
4


Bước 1. Trong tích phân ở vế trái, đặt t  6  x , ta có dt  dx và

x 3

x  3  9x

9 t



9 t  t  3

.

Bước 2. Đổi cận: x  a  t  6, x  a  t  6  a .
Bước 3. Thay vào và đổi biến, vế trái viết lại thành



9x

6

x  3  9x

6a

dx .


a  6
Bước 4. Để hai vế bằng nhau, ta cần có hai cận tương ứng bằng nhau: 
 a  6.



6 a  0


A. Bước 1

B. Bước 2

C. Bước 3

D. Bước 4.

Bài 28*. Trong Giải tích, với hàm số y  f (x ) liên tục trên miền D  [a, b ] có đồ thị là một đường
cong C , người ta có thể tính độ dài của C bằng công thức
L



b

a

1   f (x ) dx .
2

Với thông tin đó, hãy tính độ dài của đường cong C cho bởi y 
A.

3
 ln 2
8

B.

31
 ln 4
24

C.

x2
 ln x trên [1;2] :
8

3
 ln 2
8

D.

31
 ln 4
24

Bài 29. Phần ảo của số phức (1  i)2 là bao nhiêu?
A. 2

B. 0

C. 2i

D. 2i

Bài 30. So sánh môđun của hai số phức sau: z 1  3  2i và z 2  2  3i ?
A. z 1  z 2

B. z 1  z 2

C. z 1  z 2

D. z 1   z 2

Bài 31. Cho các số phức z1  2  3i, z 2  i, z 3  5  i, z 4  3  3i . Gọi A, B,C , D lần lượt là
các điểm biểu diễn của z1, z 2, z 3 , z 4 . Hỏi tứ giác ABCD là hình gì?
A. Hình vuông

B. Hình chữ nhật

C. Hình bình hành

D. Hình thang cân

Bài 32. Tìm số phức z  0 thỏa mãn điều kiện sau:
A. 3  i

B. 2  i

C. 3

2 1
  1.

z z

D. 2i

5


Bài 33. Gọi z1, z 2 là các nghiệm phức của phương trình z 2  2z  5  0 trong đó z 1 có phần ảo
dương. Tìm số phức liên hợp của số phức z 1  2z 2 .
A. 3  i

B. 3  2i

C. 3  2i

D. 2  i

Bài 34*. Gọi T là tập hợp các số phức z thỏa mãn điều kiện z  i  z  2  3i . Gọi a là
môđun nhỏ nhất của z với mọi z  T . Khi đó, giá trị của a là?
A.

3 5
5

B.

13

C. 1

D.

3
.
2

Bài 35. Hình chóp S .ABC có cạnh bên SA  (ABC ) và tam giác ABC vuông tại B . Biết rằng
AS  a, AB  2a, AC  3a, , hỏi thể tích hình chóp là bao nhiêu?
A. a

3

B. 2a

3

2a 3 5
C.
3

a3 5
D.
3

Bài 36. Từ một mảnh giấy hình vuông cạnh là 4cm , người ta gấp nó thành 4 phần đều nhau rồi
dựng lên thành một hình lăng trụ tứ giác đều như hình vẽ.

Hỏi thể tích của lăng trụ này là bao nhiêu?
A. 4cm 3

B. 16cm 3

C.

4
cm 3
3

D.

64
cm 3
3

Bài 37. Hình chóp tứ giác đều S .ABCD có góc tạo bởi mặt bên và mặt đáy là 45 . Thể tích của
4
hình chóp là a 3 . Hỏi cạnh hình vuông mặt đáy bằng bao nhiêu?
3
A. a

B. 2a

C. 4a

D. a 2

Bài 38*. Cho hình hộp chữ nhật ABCD.A B C D  có tổng diện tích tất cả các mặt là 36 , độ dài
đường chéo AC  bằng 6. Hỏi thể tích của hình hộp lớn nhất là bao nhiêu?
A. 8

B. 12

C. 8 2

D. 24 3

Bài 39. Hình lập phương ABCD.A B C D  cạnh a . Tính thể tích hình cầu ngoại tiếp của hình
lập phương này.
6


A.

4 3
a
3

B.

a 3 2
3

C.

 3a 3
2

D.  3a 3

Bài 40. Hình chữ nhật ABCD có tỷ lệ cạnh AB : AD  2 : 3 . Khi quay hình chữ nhật quanh

cạnh AB , ta thu được hình trụ có thể tích V1 ; còn khi quay hình chữ nhật quanh cạnh AD, ta thu
được hình trụ có thể tích V2 . Tính tỷ số
A.

3
2

B.

4
9

V1

V2

.

C.

9
4

D.

2
3

Bài 41. Người ta đặt được một tam giác đều ABC cạnh là 2a vào một hình nón sao cho A trùng
với đỉnh của hình nón, còn BC đi qua tâm của mặt đáy hình nón. Tính thể tích hình nón.

A.

a 3 3
6

B.

a 3 3
2

C.

2a 3 3
3

D.

Bài 42*. Hình chỏm cầu với dạng như hình vẽ có công thức thể tích là

a 3
3
h(3R 2  h 2 )
.
6

trong đó h là chiều cao của chỏm cầu và R là bán kính hình cầu ban đầu.
Có một trái dưa hấu hình cầu có bán kính là R . Người ta dùng dao cắt một phần của trái dưa hấu
ra với dạng hình chỏm cầu. Tiếp theo, người ta dùng một cái ống khoét thủng một lỗ tròn chưa rõ
bán kính ngay ở giữa lát dưa (lỗ này đi qua tâm của bề mặt lát dưa). Biết rằng chiều cao của lỗ là
12 cm. Tính thể tích của phần dưa còn lại trên lát dưa.

A. Không đủ thông tin để tính

B. 96 cm 3

C. 288 cm3

D. 144 cm3 .



Bài 43. Tích có hướng của u  (1;2; 3) và v  (3;2;1) là?

A. (1;1;1)

B. ( 4;  8;  4)

C. (4; 8; 4)

D. (1; 2;1)

Bài 44. Điểm đối xứng với A(1;2; 3) qua mặt phẳng x  y  z  3 là?
A. B(1; 0;1)

B. B(1; 1; 0)

C. B (1; 1; 1)

D. B (0;1; 0) .

Bài 45. Cho A(0;1;1), B (1; 3;2) và (P ) : x  2y  2z  2  0 . Hỏi mặt cầu (S ) nào sau đây có

bán kính là 1?
7


A. Mặt cầu (S ) có đường kính AB .
B. Mặt cầu (S ) tâm A và tiếp xúc với (P ) .
C. Mặt cầu (S ) tâm B và tiếp xúc với (P ) .
D. Mặt cầu tâm A , đi qua B .


Bài 46. Cho hai vectơ a, b tùy ý khác 0 , hỏi nhận xét nào sau đây là sai?

 
 
 
A. a, b    b, a  .
 
 
 

B. Nếu a  b  0 thì a, b vuông góc với nhau.





 
C. Nếu a, b   0 thì tồn tại số thực k sao cho a  kb .
 
  

D. Nếu a  b  0 thì độ dài của hai vectơ này khác nhau.
Bài 47. Cho tam giác ABC có tọa độ các đỉnh là A(0; 0;2), B(1; 0;1),C (3; 1; 0). Hỏi tọa độ trực
tâm của tam giác này là bao nhiêu?
A. (1;2; 1)

B. (5; 3; 0)

C. (0;5; 3)

D. (1;1; 0)

Bài 48. Cho hai mặt cầu đồng tâm I (1;2; 3) và bán kính lần lượt là R1  1, R2  5. Một mặt cầu
thứ ba tiếp xúc với cả hai mặt cầu này thì có thể có bán kính bằng bao nhiêu?
A. R  2

B. R  3

C. R  1

D. Cả A, B đều đúng.

Bài 49. Hai điểm A, B nằm trên mặt cầu có phương trình (x  4)2  (y  2)2  (z  2)2  9. Biết
rằng AB song song với OI , trong đó O là gốc tọa độ và I là tâm của mặt cầu. Viết phương trình
mặt phẳng trung trực AB.
A. 2x  y  z  6  0.
B. 2x  y  z  4  0 .
C. 2x  y  z  12  0 .
D. Chưa đủ thông tin để viết.
Bài 50*. Cho các điểm A(0;1;1), B(1; 0;1),C (1;1; 0), D(2; 3; 4) . Hỏi có bao nhiêu điểm P cách
đều các mặt phẳng (ABC ),(BCD ),(CDA),(DAB ) ?

A. 5

B. 0

C. 1

D. 4

8