Bài toán sắp xếp mờ dùng trong đánh giá theo hướng tiếp cận đại số gia tử

ĐẠI HỌC THÁI NGUYÊN
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN VÀ TRUYỀN THÔNG

NGUYỄN THỊ HUỆ

BÀI TOÁN SẮP XẾP MỜ DÙNG
TRONG ĐÁNH GIÁ THEO HƯỚNG
TIẾP CẬN ĐẠI SỐ GIA TỬ

LUẬN VĂN THẠC SĨ KHOA HỌC MÁY TÍNH


Thái Nguyên - 2012


ĐẠI HỌC THÁI NGUYÊN
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN VÀ TRUYỀN THÔNG

NGUYỄN THỊ HUỆ

BÀI TOÁN SẮP XẾP MỜ DÙNG
TRONG ĐÁNH GIÁ THEO HƯỚNG
TIẾP CẬN ĐẠI SỐ GIA TỬ
Chuyên ngành: Khoa học máy tính
Mã số: 60.48.01

LUẬN VĂN THẠC SĨ KHOA HỌC MÁY TÍNH

NGƯỜI HƯỚNG DẪN KHOA HỌC
TS.Trần Thái Sơn

Thái Nguyên - 2012


LỜI CAM ĐOAN
Tên tôi là : Nguyễn Thị Huệ
Sinh ngày 12 tháng 12 năm 1983
Học viên cao học lớp: K9B- trường Đại học CNTT&TT Thái Nguyên
Xin cam đoan : Đề tài luận văn“Bài toán sắp xếp mờ dùng trong
đánh giá theo hướng tiếp cận đại số gia tử” do TS.Trần Thái Sơn hướng
dẫn là công trình nghiên cứu của riêng tôi. Tất cả tài liệu tham khảo đều có
nguồn gốc, xuất xứ rõ ràng.
Tôi xin cam đoan tất cả những nội dung trong luận văn đúng như nội
dung trong đề cương và yêu cầu của thầy giáo hướng dẫn. Nếu sai tôi xin hoàn
toàn chịu trách nhiệm trước Hội đồng khoa học và trước pháp luật.
Thái Nguyên, ngày 15 tháng 9 năm 2012
Người cam đoan

Nguyễn Thị Huệ


LỜI CẢM ƠN
Trong quá trình làm luận văn vừa qua, dưới sự giúp đỡ và chỉ bảo nhiệt
tình của TS. Trần Thái Sơn – Viện Công nghệ thông tin – Viện khoa học Việt
Nam, luận văn của tôi đã được hoàn thành. Mặc dù đã cố gắng không ngừng
cùng với sự tận tâm của thầy hướng dẫn nhưng do thời gian và khả năng vẫn
còn hạn chế nên luận văn khó tránh khỏi những thiếu sót.
Để hoàn thành luận văn này, em xin bày tỏ lòng biết ơn sâu sắc đến TS
Trần Thái Sơn – Người thầy đã tận tình giúp đỡ em trong suốt quá trình làm
luận văn.
Em cũng xin bày tỏ lòng biết ơn đến ban lãnh đạo và các thầy giáo, cô

giáo trong Trường Đại học Công Nghệ Thông Tin & Truyền Thông Đại Học
Thái Nguyên đã giúp đỡ, tạo điều kiện tốt nhất cho em học tập và thực hiện
luận văn này.
Thái Nguyên, ngày 15 tháng 9 năm 2012
Tác giả

Nguyễn Thị Huệ


6
MỤC LỤC
Trang
Mục
lục
.................................................................................................................
...i
Danh
mục
các
ký
hiệu,
các
chữ
viết
tắt
.................................................................................................................
.iii
Danh mục hình ảnh…………………………………………………………...iv
PHẦN MỞ ĐẦU…………………………………………………………….1
CHƯƠNG 1. NHỮNG KIẾN THỨC CƠ BẢN VỀ LÝ THUYẾT TẬP

MỜ
1.1. Kiến thức cơ sở về tập mờ………………………………………………..3
1.2. Lôgic mờ …………………………………………………………………8
1.3. Biến ngôn ngữ…………………………………………………………...13
1.4. Bài toán sắp xếp mờ …………………………………………………….14
1.4.1. Bài toán kết nhập……………………………………………………14
1.4.2. Các phương pháp giải bài toán sắp xếp mờ…………………………15
1.4.2.1. Phương pháp tính toán ngôn ngữ dựa trên nguyên lý mở rộng
của tập mờ...……………………………………………………………..15
1.4.2.2. Phương pháp tính toán trên các ký hiệu ngôn ngữ ………...........16
1.3.2.3. Phương pháp tính toán ngôn ngữ dựa trên biểu diễn dữ liệu bộ 2...
…………………………………………………………………………..17
1.4.2.4. Phương pháp tính toán ngôn ngữ dựa trên biểu diễn dữ liệu bộ 3..


7
....................................................................................................................18
CHƯƠNG 2. NHỮNG KIẾN THỨC CƠ BẢN VỀ ĐẠI SỐ GIA TỬ
2.1. Đại số gia tử ……………………………………………………………19
2.2. Định nghĩa đại số gia tử ………………………………………………...21
2.3. Các định lý ……………………………………………………………...23
2.4. Các đại lương đo trên đại số gia tử ……………………………………..25
2.5. Một số tính chất của quan hệ thứ tự trong đại số gia tử ………………...27
CHƯƠNG 3. PHƯƠNG PHÁP GIẢI BÀI TOÁN SẮP XẾP MỜ THEO
CÁCH TIẾP CẬN CỦA ĐẠI SỐ GIA TỬ
3.1. Thuật toán giải bài toán sắp xếp mờ dùng trong đánh giá theo hướng tiếp
cận của đại số gia tử………………………………………………………….33
3.1.1.Bài toán……………………………………………………………...33
3.1.2. Xác định bài toán… ………………………………………………..34
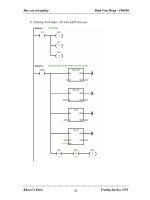
3.1.3. Thuật giải………………. ………………………………………….37

3.2. Thuật toán sắp xếp mờ sử dụng quan hệ thứ tự của các phần tử của đại số
gia tử ………………………………………………………………………...37
3.3. Chương trình thử nghiệm ……………………………………………….38
3.3.1. Cài đặt chương trình ………………………………………………..38
3.3.2. Giao diện chương trình……………………………………………...39
KẾT LUẬN………………………………………………………………….40
TÀI LIỆU THAM KHẢO …………………………………………………41
PHẦN PHỤ LỤC …………………………………………………………..43


8

DANH MỤC CÁC KÝ HIỆU, CÁC CHỮ VIẾT TẮT
Các kí hiệu,
các chữ viết tắt
ĐSGT
α
β
AX, AT
AX
W

Ý nghĩa
Đại số gia tử
Tổng độ đo tính mờ của các gia tử âm
Tổng độ đó tính mờ của các gia tử dương
Đại số gia tử
Đại số gia tử tuyến tính đầy đủ
Phần tử trung hòa trong đại số gia tử

9

DANH MỤC CÁC HÌNH ẢNH

Hình
Hình 1
Hình 2

Mô tả
Đồ thị biểu diễn hàm thuộc của tập mờ già (old)
Biểu diễn bộ 2

Hình 3

Độ đo tính mờ của biến TRUTH

Hình 4

Giao diện của chương trình

Hình 5

Kết quả thực hiện chương trình thử nghiệm


10

PHẦN MỞ ĐẦU
Trong đời sống hàng ngày hay trong công việc giảng dạy, chúng ta

thường xuyên gặp phải yêu cầu phải lựa chọn, đánh giá. Chẳng hạn, đánh giá
học sinh trong trường học hay lựa chọn phương án tối ưu trong các phương án
được đưa ra. Nếu việc lựa chọn có thể dựa trên các đánh giá bằng điểm số thì
thông thường người ta lấy trung bình (có thể có trọng số) của các đánh giá rồi
dựa trên kết quả tổng hợp này mà sắp xếp các đối tượng và trên cơ sở đó đưa
ra quyết định. còn nếu ta chỉ có các đánh giá bằng những từ ngữ của ngôn ngữ
tự nhiên (như “giỏi”, “rất khá”..) thì việc tìm ra kết quả tổng hợp cho đánh giá
là khó khăn hơn nhiều vì nhiều khi không hiểu, (“khá” +”giỏi”)/2 sẽ là cái gì.
Nội dung chính của bài toán sắp xếp là phần tổng hợp các ý kiến đánh giá
(bằng số hoặc từ ngữ) thành một đánh giá kết quả và thông thường được gọi là
bài toán kết nhập. Đã có nhiều nghiên cứu được tiến hành để giải quyết bài
toán sắp xếp, tựu trung có thể phân làm 2 hướng chính: hướng nghiên cứu dựa
vào lý thuyết tập mờ và hướng nghiên cứu dựa trên chỉ số thứ tự của các từ
đánh giá trong quan hệ thứ tự tự nhiên. Hướng nghiên cứu dựa trên lý thuyết
tập mờ chủ yếu tập trung vào việc chuyển các từ đánh giá vào trường số thực,
trên cơ sở đó tiến hành các phép kết nhập trên các số thực. Hướng nghiên cứu
dựa trên chỉ số thứ tự của các từ đánh giá dựa trên quan sát là các từ dùng
được đánh giá thông thường có thể sắp xếp theo thứ tự (thí dụ như “giỏi” >
“tương đối giỏi”>”khá”> “trung bình”> “kém”...) và trong tập thứ tự đó, mỗi
từ được ứng với một chỉ số. Các phép kết nhập cần thiết sẽ được tiến hành
trên tập các chỉ số thay vì trên tập các từ đánh giá. Mỗi hướng nghiên cứu nêu
trên đều có những ưu khuyết điểm riêng liên quan đến sai số có thể gặp phải,
đến độ phức tạp tính toán... Trong luận văn này, tôi đi theo hướng nghiên cứu
sau, tức là dựa cơ bản trên chỉ số thứ tự của các từ đánh giá để thực hiên các


11

phép kết nhập, tuy nhiên luận văn sẽ sử dụng cách tiếp cận Đại số gia tử
(ĐSGT) để giải quyết bài toán sắp xếp. Các kết quả nghiên cứu cho thấy cách

tiếp cận ĐSGT cho những đánh giá phù hợp trên cơ sở thuật toán khá đơn
giản về mặt thực thi. Nên tôi quyết định lựa chọn đề tài luận văn “Bài toán
sắp xếp mờ dùng trong đánh giá theo hướng tiếp cận đại số gia tử”
Luận văn có bố cục như sau:
Chương 1: Những kiến thức cơ bản về lý thuyết tập mờ
Trong chương này trình bày những kiến thức cơ bản về lý thuyết tập
mờ, bài toán sắp xếp mờ và một số phương pháp giải bài toán sắp xếp mờ.
Chương 2: Những kiến thức cơ bản về đại số gia tử
Trong chương này trình bày khái niệm về đại số gia tử, các định lý, các
đại lương đo trên đại số gia tử, một số tính chất của quan hệ thứ tự trong đại
số gia tử.
Chương 3 : Phương pháp giải bài toán sắp xếp mờ theo cách tiếp cận của
đại số gia tử.
Trong chương này trình bày bài toán, thuật toán và cách giải bài toán
sắp xếp mờ theo hướng tiếp cận của đại số gia tử bằng cách sử dụng quan hệ
thứ tự của các từ trong đại số gia tử.


12

Chương 1
NHỮNG KIẾN THỨC CƠ BẢN VỀ LÝ THUYẾT TẬP MỜ
1.1. Kiến thức cơ sở về tập mờ
Là người khởi xướng cho lý thuyết tập mờ, L. A. Zadeh đã có rất nhiều
nghiên cứu mở đường cho sự phát triển và ứng dụng [14]. Ý tưởng nổi bật của
Zadeh là từ những khái niệm trừu tượng về ngữ nghĩa của thông tin mờ,
không chắc chắn như trẻ-già, nhanh-chậm, cao-thấp,… Ông đã tìm cách biểu
diễn chúng bằng một khái niệm toán học, được gọi là tập mờ và được định
nghĩa như sau.
Định nghĩa 1. [14] Cho một tập vũ trụ U với các phần tử ký hiệu bởi x,

U={x}. Một tập mờ A trên U là tập được đặc trưng bởi một hàm µA(x) mà nó
liên kết mỗi phần tử x∈U với một số thực trong đoạn [0,1]. Giá trị hàm µA(x)
biểu diễn mức độ thuộc của x trong A. µA(x) là một ánh xạ từ U vào [0,1] và
được gọi là hàm thuộc của tập mờ A.
Như vậy, giá trị hàm µA(x) càng gần tới 1 thì mức độ thuộc của x trong A
càng cao. Khi A là một tập hợp kinh điển, hàm thuộc của nó, µA(x), chỉ nhận 2
giá trị 1 hoặc 0, tương ứng với x có nằm trong A hay không. Rõ ràng, tập mờ
là sự mở rộng của khái niệm tập hợp kinh điển. Các khái niệm, phép toán
trong lý thuyết tập kinh điển cũng được mở rộng cho các tập mờ.
Họ tất cả các tập mờ trên miền cơ sở U là không gian các hàm từ U vào

F (U ,[0,1])

đoạn [0,1], tức là
= {µA : U→[0,1]}, một không gian tương đối
giàu về cấu trúc tính toán mà nhiều nhà nghiên cứu đã sử dụng cho việc mô
phỏng các phương pháp suy luận của con người.
Chúng ta có thể biểu diễn tập mờ bằng các cách sau, tùy theo tập U là
hữu hạn, đếm được hay vô hạn liên tục:
- Trường hợp U hữu hạn, U={ui : 1≤ i ≤ n}, ta có thể viết


13

A = µA(u1)/u1 + µA(u2)/u2 + … + µA(un)/un = ∑1≤ i ≤n µA(ui)/ui
- Trường hợp U vô hạn đếm được, U={ui : i=1,2,… }, ta viết
A = ∑1≤ i <∞ µA(ui)/ui
- Trường hợp U vô hạn liên tục, U=[a,b], ta viết
b

∫µ

A

A=

(u ) / u

a

Sau đây ta định nghĩa một số khái niệm đặc trưng liên quan đến tập mờ.
Định nghĩa 2. [1] Cho một tập mờ A trên tập vũ trụ U và α∈[0,1]. Tập
lát cắt α của A là một tập kinh điển, ký hiệu Aα, được xác định như sau :
Aα = {u ∈ U : µA(u)≥α}.
Tập Aα còn gọi là tập mức α của A.
Định nghĩa 3. [1] Cho một tập mờ A trên tập vũ trụ U,
i) Giá của tập mờ A, ký hiệu support(A), là tập con của U trên đó

µA(u)≠0, tức là support(A) = {u ∈ U : µA(u)≥0}.
ii) Độ cao của tập mờ A, ký hiệu high(A), là cận trên đúng của hàm
thuộc µA(u) trên U, tức là high(A) = sup{µA(u) : u∈U}.
iii) A được gọi là tập mờ chuẩn nếu high(A)=1. Ngược lại gọi là tập
mờ dưới chuẩn.
iv) Lõi của tập mờ A, ký hiệu core(A), là một tập con của U được
xác định như sau:
core(A) = {u∈U : µA(u) = high(A)}.
Định nghĩa 4. [1] Cho một tập mờ A trên tập vũ trụ U,
i) Lực lượng vô hướng hay bản số của tập mờ A, ký hiệu count(A),
được xác định là:
count(A) = ∑u∈U µA(u), nếu U là hữu hạn hay đếm được,

14

= ∫U µA(u)du, nếu U là vô hạn liên tục.
ii) Lực lượng mờ hay bản số mờ của tập mờ A, ký hiệu card(A), là
một tập mờ trên tập các số nguyên không âm N, được xác định như sau:
card(A) = ∫N µcard(A)(n)dn , trong đó, µcard(A)(n) được xác định
theo công thức sau, với |Aα| là lực lượng tập mức Aα,

µcard(A)(n) = sup{t∈[0,1] : |Aα| = n}.
Ví dụ 1. Cho tập vũ trụ chỉ tuổi tính chẵn năm U={u : 0≤ u ≤120}, A là
một tập mờ chỉ tuổi già (old) được xác định bởi hàm thuộc sau (hình 1):
u ∈ [0, 60]
0
µold (u ) = 
u − 60 −2 −1
(1 + ( 6 ) ) u ∈ [61,120]

Khi đó tập mức α=0.5 của A là A0.5 = {u : 66≤ u ≤120} ;
support(A) = {u : 61≤ u ≤120} ; high(A) = 1.01-1; core(A) = {120}.

Hình 1. Đồ thị biểu diễn hàm thuộc của tập mờ già (old)
Tiếp theo chúng ta định nghĩa một số phép toán cơ bản trên tập mờ, các
phép này làm cơ sở cho việc phát triển lôgíc mờ sau này.
Định nghĩa 5. [1,14] Cho hai tập mờ A và B trên tập nền U có hàm thuộc
tương ứng là µA và µB, ba phép toán cơ bản là hợp, giao của hai tập mờ và lấy
phần bù của tập mờ A là một tập mờ C, được viết là
C = A ∪ B, hoặc C = A ∩ B, hoặc C = A~ với hàm thuộc được xác
định như sau:

µA∪B(u) = max(µA(u), µB(u)), ∀u ∈ U,

µA∩B(u) = min(µA(u), µB(u)), ∀u ∈ U,


15

µA~(u) = 1- µA(u), ∀u ∈ U.
Hay viết ở dạng thu gọn là

µA∪B(u) = µA(u) ∨ µB(u)),
µA∩B(u) = µA(u) ∧ µB(u)).
Ví dụ 2. [1] Xét tập nền U = {1,2,3,4,5,6,8,9,10,11} là tập các giá trị
trong thang điểm 10 đánh giá kết quả học tập của học sinh. Hai tập mờ G và K
tương ứng là hai khái niệm mờ về năng lực học giỏi và học kém, với hàm
thuộc được cho dưới dạng bảng như sau:
u∈U
µG(u
)
µK(u
)

1
2
3
4
5
6
7
8

9 10
0.0 0.0 0.0 0.1 0.3 0.5 0.7 0.9 1.0 1.0
1.0 0.9 0.8 0.6 0.4 0.2 0.0 0.0 0.0 0.0

Ta có kết quả của các phép toán trên hai tập mờ này với hàm thuộc thể
hiện trong bảng sau:
u∈U
µG∪K(u)
µG∩K(u)
µG~(u)

1
2
3
4
5
6
7
8
9 10
0.0 0.0 0.0 0.6 0.5 0.5 0.7 0.9 1.0 1.0
0.0 0.0 0.0 0.1 0.3 0.2 0.0 0.0 0.0 0.0
1.0 1.0 1.0 0.9 0.7 0.5 0.3 0.1 0.0 0.0

Một lớp đặc biệt các tập mờ là lớp các quan hệ mờ, chúng là các tập mờ
trên không gian tích Đề-các các miền cơ sở. Như tên gọi, quan hệ mờ mô tả
mối quan hệ mờ giữa các đối tượng trong miền cơ sở. Về mặt hình thức chúng
ta định nghĩa quan hệ mờ như sau.
Định nghĩa 6. [1] Cho U là tích Đề-Các của n miền cơ sở Ui, i=1, ,…, n.
Khi đó mỗi một tập mờ trên U được gọi là một quan hệ mờ n-ngôi và được kí

hiệu là R, gọi là tên của quan hệ đó, và nó được biểu thị bằng công thức sau:
R=∫

U1 ×...×U n

µ (u1 ,..., u1 ) / (u1 ,..., u1 )


16

Trong đó µ(u1,…,un) là hàm thuộc của tập mờ R. Dấu ∫ biểu diễn hình
thức của hàm thuộc, có thể một trong ba trường hợp là hữu hạn hoặc đếm
được hoặc liên tục.
Quan hệ mờ cũng có các phép tính cơ bản như trên tập mờ vì bản thân nó
cũng là tập mờ. Ngoài ra, quan hệ mờ có những phép tính đặc thù riêng mà
trên tập mờ không có, đó là phép hợp thành dưới đây.
Định nghĩa 7. [1] Cho R là một quan hệ mờ trên U×V và S là quan hệ
mờ trên V×W. Khi đó, phép hợp thành của hai quan hệ này là một quan hệ
trên U×W, được ký hiệu là R°S và được định nghĩa như sau:
R°S = ∫∨v∈V [µR(u,v)°µS(v,w)]/(u,w)
Trong đó ° là một phép tính 2 ngôi trong [0,1] có tính giao hoán, kết hợp
và phân phối đối với phép max ∨. Nếu ° là phép min ∧, thì ta có phép hợp
thành max-min, nếu ° là phép nhân số học thì ta có phép hợp thành maxproduct.
Ví dụ 3. Cho U = {u1, u2, u3}, V = {v1, v2} và W = {w1, w2}, với quan hệ
mờ R trên U×V và S trên V×W được cho hàm thuộc dưới dạng ma trận
v1

v2

u1  0.4 1 

w1
w2
R = u2  1 0.3
v  0.2 0.8
S= 1
u3 0.7 0.8
v2  0.7 0.1
và
w1

w2

u1 0.7 1 
R oS = u2  0.3 0.8 
u3 0.7 0.7 
khi đó phép hợp thành max-min là
,
w1

w2

u1  0.8 0.32 
R oS = u2  0.21 0.8 
u3 0.56 0.56
và max-product là
.


17

Phép hợp thành các quan hệ mờ đóng vai trò quan trọng trong quá trình
lập luận xấp xỉ sau này.
Trong hầu hết các ứng dụng, tri thức được biểu diễn dưới dạng luật “ifthen” và mỗi luật được xem như một quan hệ mờ
Chúng ta thấy rằng lý thuyết tập mờ với mục tiêu mô hình hóa toán học
ngữ nghĩa của các khái niệm mờ và, hơn nữa, mô hình hóa cách lập luận của
con người. Tuy nhiên, những vấn đề này thuộc loại có cấu trúc yếu, khó có thể
có một cấu trúc toán duy nhất mô hình hóa trọn vẹn những vấn đề đó
1.2. Lôgic mờ
Cùng với khái niệm biến ngôn ngữ, L. A. Zadeh đã phát triển lôgic mờ
mà các giá trị chân lý nhận trong T(Truth) = {true, very true, more false,
possible false, very very false,…}, tập các giá trị của biến ngôn ngữ Truth. Khi
đó, một mệnh đề dạng “X is A”, với A là một khái niệm mờ, sẽ có giá trị chân
lý thuộc T(Truth) và được biểu thị bởi một tập mờ có hàm thuộc µA trên không
gian tham chiếu U.
Lý thuyết tập mờ là cơ sở toán học cho việc phát triển các phương pháp
mô phỏng lập luận của con người. Về nguyên tắc, vấn đề tư duy, lập luận của
con người rất phức tạp và do đó không thể sử dụng một cấu trúc toán học duy
nhất để mô phỏng. Vì vậy, mục tiêu của chúng ta là càng xây dựng được nhiều
cấu trúc đại số các tập mờ càng tốt để linh hoạt trong tiếp cận các vần đề ứng
dụng. Ở đây, chúng ta sẽ định nghĩa một họ các cặp đối ngẫu t-norm và tconorm cùng với phép phủ định làm cơ sở cho lôgic mờ và lập luận xấp xỉ.
Định nghĩa 8 [1] Một hàm 2-biến T : [0,1]×[0,1] → [0,1] được gọi là
phép t-norm nếu nó thỏa các tính chất sau với ∀a,a’,b,c ∈[0,1]:
i) Tính chất điều kiện biên:

T(a,1) = a

ii) Tính giao hoán:

T(a,b) = T(b,a)

iii) Tính đơn điệu:

a ≤ a’ ⇒ T(a,b) ≤ T(a’,b)


18

iv) Tính kết hợp:

T(a,T(b,c)) = T(T(a,b),c)

Ngoài ra, một số tính chất khác cần đòi hỏi phải có trong nhiều ứng dụng
đối với phép t-norm bao gồm:
v) Tính liên tục:

T là hàm hai biến liên tục

vi) Tính lũy đẳng dưới:

T(a,b) < a

vii) Tính đơn điệu chặt:

a ≤ a’ và b ≤ b’ ⇒ T(a,a’) <

T(b,b’)

Định nghĩa 9 [1] Một hàm 2-biến S : [0,1]×[0,1] → [0,1] được gọi là
phép t-conorm nếu nó thỏa các tính chất sau với ∀a,a’,b,c ∈[0,1]:
i) Tính giới nội:

S(a,0) = a

ii) Tính giao hoán:

S(a,b) = S(b,a)

iii) Tính đơn điệu:

a ≤ a’ ⇒ S(a,b) ≤ S(a’,b)

iv) Tính kết hợp:

S(a,S(b,c)) = S(S(a,b),c)

Như vậy, chỉ có hai tính chất điều kiện biên và giới nội làm nên sự khác
biệt giữa hai họ phép tính t-norm và t-conorm.
Chúng ta cũng có thể mở rộng định nghĩa cho phép t-norm và t-conorm
này đối với trường hợp nhiều biến vào, tức là Tex : [0,1]n → [0,1] và Sex : [0,1]n
→ [0,1], bằng cách áp dụng liến tiếp các phép t-norm và t-conorm ở trên.
Định nghĩa 10 [1] Hàm N : [0,1] → [0,1] được gọi là phép phủ định
(negation) nếu nó thỏa các tính chất sau với ∀a,a’ ∈[0,1]:
i) Tính đơn điệu giảm:
iv) Tính lũy đẳng:

a ≤ a’ ⇒ N(a) ≥ N(a’)

N(N(a)) = a

Ví dụ 4: Các phép t-norm, t-conorm và phép phủ định hay được sử dụng

như:


19

TM(a,b) = min{a,b}
TP(a,b) = a.b
TL(a,b) = max{0,a+b-1}
a

T * (a, b) = b
0


khi b = 1
khi a = 1
khi a ≠ 1& b ≠ 1

SM(a,b) = max{a,b}
SP(a,b) = a+b-a.b
SL(a,b) = min{1,a+b}
a

S (a, b) = b
0

*

khi b = 0
khi a = 0

khi a ≠ 0& b ≠ 0

N(a) = 1-a.
Định nghĩa 11 [1] Ba phép tính t-norm T, t-conorm S và phép phủ định
N được gọi là một hệ đối ngẫu (T,S,N) nếu chúng thỏa điều kiện sau:
N(S(a,b)) = T(N(a),N(b)), ∀a,b∈[0,1].
Việc áp dụng các phép t-norm, t-conorm và phép phủ định cho việc tính
toán các toán tử hội, tuyển và phủ định trong lôgic mờ làm tăng tính mềm dẻo
trong ứng dụng. Thực vậy, khi hai mệnh đề “X is A” và “X is B” có giá trị
chân lý được biểu thị bởi hai hàm thuộc tương ứng µA và µB trên không gian
tham chiếu U và V thì mệnh đề mờ “X is A and B” có hàm thuộc biểu thị giá
trị chân lý là µA∩B = T(µA,µB), với T là một t-norm nào đó. Tương tự, mệnh đề
“X is A or B” có hàm thuộc là µA∪B = S(µA,µB) và mệnh đề “X is not A” có hàm
thuộc là µ~A = N(µA), ở đây S là một t-conorm và N là một phép phủ định được
chọn nào đó.
Các mệnh đề mờ cùng với giá trị chân lý của chúng là những đối tượng
nghiên cứu chính của lôgíc mờ. Trong đó, một dạng mệnh đề mờ thường biểu


20

diễn cho tri thức dạng luật trong lập luận xấp xỉ và ứng dụng, đó là mệnh đề
mờ có điều kiện dạng “If X is A then Y is B” và được biểu diễn bằng toán tử
kéo theo mờ.
Ở đây, một cách tổng quát, chúng ta đưa ra một số tính chất cho một
phép kéo theo mờ.
Định nghĩa 12 [1] Phép kéo theo là một hàm số I : [0,1]2 → [0,1] có các
tính chất sau:
i) Tính đơn điệu giảm đối với biến thứ nhất
x ≤ z ⇒ I(x,y) ≥ I(z,y), ∀y∈[0,1]

ii) Tính đơn điệu tăng đối với biến thứ hai
y ≤ u ⇒ I(x,y) ≤ I(x,u), ∀x∈[0,1]
iii) Tính chi phối của giá trị chân lý sai
I(0,x) = 1
iv) Tính trung tính của giá trị chân lý đúng
I(1,x) = x
v) Tính đồng nhất
I(x,x) = x
vi) Tính chất hoán đổi
I(x,I(y,z)) = I(y,I(x,z))
vii) Tính chất về điều kiện giới nội
I(x,y) = 1 nếu và chỉ nếu x ≤ y
viii) Tính chất khái quát hóa của phép kéo theo kinh điển
I(x,y) = I(N(y),N(x)), trong đó N là phép phủ
định
ix) I là hàm liên tục theo cả hai biến.


21

Rõ ràng mệnh đề điều kiện ở dạng “If X is A then Y is B” thể hiện mối
quan hệ giữa hai khái niệm mờ A và B. Vì vậy, chúng cảm sinh một quan hệ
mờ R thể hiện bởi một tập mờ trên không gian tích Đề-Các U×V được xác
định bởi hàm thuộc thông qua một phép kéo theo được chọn.
Ví dụ 5. Một số dạng phép kéo theo thường dùng
Mamdani
I(x,y) = min{x,y}
Dạng khái quát từ phép kéo theo kinh điển
I(x,y) = S(N(x),y), hoặc
I(x,y) = S(N(x),T(x,y)), hoặc

I(x,y) = S(T(N(x),N(y)),y), với T, S và N là các phép
t-norm, t-conorm và phép phủ định.
Reichenbach
I(x,y) = 1-x+x.y
Lukasiewicz
I(x,y) = min{1, 1-x+y}.
Định lý sau đây cho chúng ta xem xét liệu phép kéo theo như thế nào sẽ
thỏa mãn tất cả các tính chất trong định nghĩa 12.
Định lý 1. [1] Một hàm 2-biến I : [0,1]2 → [0,1] thỏa các tính chất từ i)
đến ix) trong định nghĩa 12 nếu và chỉ nếu có tồn tại một hàm liên tục đơn
điệu tăng thực sự f : [0,1] → [0,+∞) sao cho f(0) = 0 và
I(x,y) = f-1(f(1)-f(x)+f(y)), với ∀x,y ∈ [0,1], và
N(x) = f-1(f(1)-f(x)), với ∀x ∈[0,1].


22

Tuy nhiên, bản chất ngữ nghĩa của phép kéo theo mờ trong lập luận của
con người rất phức tạp, khó có một hệ tiên đề chung cho mọi tình huống. Vì
vậy, các tính chất ở định nghĩa 12 không bắt buộc mọi phép kéo theo mờ đều
phải thỏa mãn. Hơn nữa, cũng không có quyền đặt ra các yêu cầu về một tính
chất nào đó khác mà một phép kéo theo cần phải có. Chỉ có ứng dụng thực
tiễn là tiêu chuẩn cuối cùng chứng minh tính phù hợp của một định nghĩa
phép kéo theo mờ.
1.3. Biến ngôn ngữ
Trong [14], L. A. Zadeh đã viết “Khi thiếu hụt tính chính xác bề ngoài
của những vấn đề phức tạp cố hữu, một cách tự nhiên là tìm cách sử dụng các
biến ngôn ngữ, đó là các biến mà giá trị của chúng không phải là số mà là
các từ hoặc các câu trong ngôn ngữ tự nhiên hoặc nhân tạo. Động lực cho
việc sử dụng các từ, các câu hơn các số là ở chỗ đặc trưng ngôn ngữ của các

từ và các câu thường ít xác định cụ thể hơn của các số”. và ông đã đưa ra một
lớp khái niệm rộng hơn có thể mô hình qua các tập mờ, đó là biến ngôn ngữ.
Định nghĩa 13. [14] Biến ngôn ngữ là một bộ năm (X,T(X),U,R,M),
trong đó X là tên biến, T(X) là tập các giá trị ngôn ngữ của biến X, U là không
gian tham chiếu hay còn gọi là miền cơ sở của biến X, R là một quy tắc ký
pháp sinh các giá trị ngôn ngữ cho T(X), M là quy tắc gán ngữ nghĩa biểu thị
bằng tập mờ trên U cho các từ ngôn ngữ trong T(X).
Ví dụ 6 Cho X là biến ngôn ngữ có tên AGE, miền tham chiếu của X là
U=[0,120]. Tập các giá trị ngôn ngữ T(AGE)={very old, old, possible old, less
old, less young, quite young, more young,…}. Chẳng hạn với giá trị ngôn ngữ
old, quy tắc gán ngữ nghĩa M cho old bằng tập mờ cho bởi ví dụ 1
M(old) = {(u,µold(u)) : u∈[0,120]}.


23

Chúng ta thấy rằng một biến ngôn ngữ được cấu trúc theo hướng mà
trong đó có hai quy tắc cơ bản. Thứ nhất là quy tắc cú pháp, qui định cách
thức để sinh các giá trị ngôn ngữ. Thứ hai là quy tắc ngữ nghĩa, qui định thủ
tục tính toán ngữ nghĩa của các giá trị ngôn ngữ. Ngoài các giá trị sinh nguyên
thủy, các giá trị ngôn ngữ có thể gồm các từ liên kết như and, or, not,… và các
gia tử ngôn ngữ như very, possible, less, quite, more,….Zadeh cũng nêu ra
một vài thí dụ về cách sinh ra các hàm thuộc từ các hàm thuộc đã có như nếu
A là nhãn ngôn ngữ mờ có hàm thuộc là μ A thì veryA có hàm thuộc là (μA)2
còn lessA có hàm thuộc là căn bặc hai của μA...
Trong thực tế có nhiều biến ngôn ngữ khác nhau về giá trị sinh nguyên
thủy, tuy nhiên cấu trúc miền giá trị của chúng tồn tại một “đẳng cấu” sai khác
nhau bởi giá trị sinh nguyên thủy này. Đây gọi là tính phổ quát của biến ngôn
ngữ.
Khác với giá trị nguyên thủy của các biến ngôn ngữ phụ thuộc vào ngữ

cảnh, ngữ nghĩa của các gia tử và các từ liên kết hoàn toàn độc lập với ngữ
cảnh. Đây là tính độc lập ngữ cảnh của gia tử và liên kết.
Chúng ta thấy rằng lý thuyết tập mờ với mục tiêu mô hình hóa toán học
ngữ nghĩa của các khái niệm mờ và hơn nữa mô hình hóa cách lập luận của
con người. Tuy nhiên, những vấn đề này thuộc loại có cấu trúc yếu, khó có thể
có một cấu trúc toán duy nhất mô hình hóa trọn vẹn những vấn đề đó.
1.4. Bài toán sắp xếp mờ
1.4. 1.Bài toán sắp xếp mờ
Một cách hình thức, bài toán kết nhập có thể được phát biểu như sau.
Giả sử người quyết định phải ra quyết định chọn một phương án “tốt nhất”


24

trong m phương án lựa chọn Ai, i = 1, …, m, trên cơ sở lấy ý kiến đánh giá
của n chuyên gia ej, j = 1, …, n.
Trong môi trường thông tin ngôn ngữ, các chuyên gia biểu thị đánh giá
của mình bằng các từ ngôn ngữ (thang đánh giá ngôn ngữ) lấy trong tập S =
{s0, …, sg}. Ký hiệu xij là ý kiến đánh giá của chuyên gia j về phương án Ai.
Một yêu cầu tự nhiên là cần định giá ý kiến tổng hợp của các chuyên
gia đối với từng phương án, nghĩa là ta cần sử dụng một phép toán kết nhập R
tích hợp các ý kiến {xij: j = 1, …, n} của các chuyên gia. Toán tử kết nhập là
một ánh xạ R : {s0, …, sg}n→ {s0, …, sg}. Ánh xạ này phải được xác định sao
cho kết quả của phép toán R(si1, …, sin) có thể xem là biểu thị ý kiến tập thể
của n chuyên gia.
Giải bài toán sắp xếp mờ cũng chính là giải bài toán kết nhập mờ vì khi
có kết quả kết nhập, ta có thể sắp xếp các kết quả này theo thứ tự tăng (giảm )
dần của kết quả đó.
Có nhiều phương pháp tiếp cận tính toán khác nhau để giải quyết vấn
đề này. Dưới đây là một số phương pháp phổ biến.

1.4.2. Các phương pháp giải bài toán sắp xếp mờ
1.4.2.1. Phương pháp tính toán ngôn ngữ dựa trên nguyên lý mở rộng
của tập mờ
Ta biết rằng bằng nguyên lý mở rộng (hay nguyên lý thác triển) các ánh xạ
hoặc các phép tính số học thông thường có thể chuyển thành các ánh xạ hay
phép tính tương ứng trên các tập mờ. Ý tưởng chính của phương pháp là các
phép tính kết nhập kinh điển như phép trung bình số học, trung bình có trọng
số …, có thể chuyển thành các phép tính tương ứng trên các tập mờ, chẳng


25

hạn phép lấy trung bình cộng mờ, trung bình cộng mờ có trọng số trên các tập
mờ … Khi đó, các từ ngôn ngữ trong tập S được xem là các nhãn của các tập
mờ. Các phép kết nhập mờ thực hiện trên các tập mờ của các nhãn trong tập S
sẽ cho kết quả là tập mờ. Nói chung tập mờ kết quả khác với các tập mờ của
các nhãn, hay nó không biểu thị cho một nhãn ngôn ngữ nào trong S. Điều này
dẫn đến sự cần thiết phải phát triển các phương pháp xấp xỉ ngôn ngữ, tức là
tìm một nhãn ngôn ngữ trong S có tập mờ xấp xỉ tập mờ kết quả.
1.4.2.2. Phương pháp tính toán trên các ký hiệu ngôn ngữ
Giả sử ý kiến đánh giá theo một tiêu chí được biểu thị bằng các từ ngôn
ngữ trong tập S = {s0, …, sg} được sắp tuyến tính theo ngữ nghĩa của chúng
sao cho: singười ta mượn cấu trúc tính toán của đoạn [0, g] bao hàm các chỉ số để thực
hiện việc kết nhập số học. Ý tưởng này thể hiện như sau:
Giả sử ta lấy kết nhập tập các từ ngôn ngữ trong A = {a 1, …, ap}, ai∈S. Ta
thực hiện một hoán vị các chỉ số của tập A, A = {aπ1, …, aπp},
sao cho aπi ≥ aπj nếu i ≤ j. Xét một phép kết nhập số học R nào đó. R sẽ cảm
sinh một phép kết nhập g* trên tập S được định nghĩa như sau:
Tính R(π1, …, πp) ∈ [0, g], với π1, …, πp là các chỉ số của các phần tử trong A.

Đặt i* = round(R(π1, …, πp)), trong đó round là phép làm tròn số học. Khi đó
phần tử si* được xem là kết quả kết nhập R*(aπ1, …, aπp).
Lưu ý rằng các chỉ số chỉ mang thông tin về thứ tự của các từ ngôn ngữ. Vì
vậy, việc thực hiện phép kết nhập R trên các chỉ số, mặc nhiên ta đã thừa nhận
ngữ nghĩa các từ của S được biểu thị bằng chỉ số của chúng.