bài tập mặt câu

TRƯỜNG THPT BA BỂ - BẮC KẠN
TỔ: TOÁN - TIN
BÀI TẬP MẶT CẦU
TIẾT: 44
Người dạy: Đàm Ngọc Hùng


Nhắc lại định nghĩa mặt cầu, một mặt cầu được xác định khi nào?
A
3
O
A
5
A
2
A
1
A
4
R
R
R
R
R
Vậy một mặt cầu xác định khi biết tâm và
bán kính của nó.
S(O;R) = {M | OM=R} (R >0)
Cho tam giác ABC vuông tại A như trên
hình vẽ.

A
B
C
O
OA =
AB
2


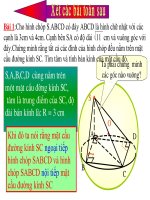
Bài 1. Chứng minh rằng 8 đỉnh của một hình hộp chữ nhật nằm trên một mặt
cầu.
O
A
B
C
D
A’
B’
C’
D’
O
A
B
C
D
A’
B’
C’
D’
c

a
b
Gọi O là giao điểm của các đường chéo, suy ra O là trung điểm của các đường
chéo đó. O cách đều các đỉnh của hình hộp chữ nhật vì các đường chéo bằng
nhau.
Gọi a, b, c lần lượt là các cạnh của hình hộp chữ nhật
Đặt: R = OA =
2 2 2
1
a b c
2
+ +
Vậy tám đỉnh của hình hộp chữ nhật nằm trên mặt cầu S(O;R).
Bài giải.


Bài 2. Cho tam giác ABC vuông tại B, đoạn DA ⊥ (ABC).
a) Xác định mặt cầu đi qua bốn điểm A, B, C, D.
b) Cho AB = 3a, BC = 4a, AD = 5a tính bán kính của mặt cầu nói trên.
O
D
A
B
C
Bài giải.
a)
BC AB
Vì BC BD
BC AD

⊥

⇒ ⊥

⊥

Gọi O là trung điểm của DC. Hai tam
giác vuông DBC và DAC có chung
cạnh huyền DC nên:
OA OB OC OD= = = =
DC
R
2
=
Vậy S(O;R) đi qua bốn điểm A, B, C, D.
So sánh độ dài các đoạn OA, OB, OC, OD.


O
D
A
B
C
b)
DC
2
= DA
2
+ AC
2

=
= DA
2
+ AB
2
+BC
2
=
= 25a
2
+ 9a
2
+ 16a
2
=
50a
2
DC
⇒ =
5 2 a
5 2
V a
2
Ëy R =