Algebra for college students 7th edition lial test bank

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Decide if the statement is true or false.
1) -4 is a solution of -3x = 12.
1) _______
A) True
B) False
2) 14 is a solution of 6x = 85.
A) True

B) False

3) 5 is a solution of 5x - 2 = 23.
A) True

B) False

4) 3 is a solution of -3x + 5 = -2.
A) True

B) False

5) -6 is a solution of -6x + 5x = 6.
A) True

B) False

6) 1 is a solution of -9x - 2x = -3.
A) True

B) False

7) 3 is a solution of -9x + 3x = -7x.
A) True

B) False

2) _______

3) _______

4) _______

5) _______

6) _______

7) _______

Decide whether the following is an expression or an equation.
8) -10x - 2 + 6x + 6
A) Equation
B) Expression
9) 8x - (7x - 1) = 2
A) Equation

9) _______
B) Expression

10) 7(4x + 2) = 2(9x - 9)
A) Equation

B) Expression

11) 3(4x + 7) - 8(5x - 4)
A) Equation

B) Expression

12) - 7x + 5 - 3x + 10 = 0
A) Equation

B) Expression

13) 5(2x - 4) = 9(x + 3)
A) Equation

B) Expression

10) ______

11) ______

12) ______

13) ______

14) -4(x - 9) - 3(x + 4) - 8x
A) Equation
Solve the equation.
15) 14x + 5 = 9
A)

16) -11s + 12 = -15s

8) _______

14) ______
B) Expression

15) ______
B)

C)

D)

16) ______


A)

17) 23t - 11 = 8t + 7
A)

B)

C)

D)

B)

C)

D)

17) ______

18) 3(x + 5) = (3x + 15)
A) {0}
C) ∅

18) ______
B) {All real numbers}
D) {30}

19) (y - 9) - (y + 6) = 8y
A)

B)

C)

D)

20) 15(4c - 2) = 5c - 3
A)

B)

C)

D)

21) 2(y + 7) = 3(y - 5)
A) {29}

B) {-1}

C) {-29}

D) {1}

22) 4m + 7 + 2(3m - 4) = 4(m + 4)
A)
B)

C)

D)

23) -3x + 2(2x - 3) = -1 - 4x
A) {-1}

B)

C)

D) {1}

24) -[8x + (4x + 3)] = 2 - (2x + 4)

A)
B)

C)

D)

19) ______

20) ______

21) ______

22) ______

23) ______

24) ______

Decide whether the equation is conditional, an identity, or a contradiction. Give the solution set.
25) 21m + 12 = 3(3m + 20)
A) Contradiction; ∅
B) Conditional; {4}
C) Conditional; {-6}
D) Identity; {all real numbers}
26) 4(24t + 16) = 16(2t - 4)
A) Conditional; {-2}
C) Conditional; {-0}

B) Contradiction; ∅

D) Identity; {all real numbers}

27) 5(2f - 31) = 10f - 155
A) Conditional; {0}
C) Identity; ∅

B) Contradiction; ∅
D) Identity; {all real numbers}

28) 2(5g + 13) - 10g - 26 = 0
A) Contradiction; ∅
C) Conditional; {0}
29) 9k + 32 = 3(3k + 8)

25) ______

26) ______

27) ______

28) ______
B) Identity; {all real numbers}
D) Conditional; {5}
29) ______


A) Contradiction; ∅
C) Identity; {all real numbers}

B) Conditional; {-3}

D) Conditional; {3}

30) -15s + 38 + 3(5s - 10) = 0
A) Identity; {all real numbers}
C) Conditional; {1}

B) Conditional; {5}
D) Contradiction; ∅

31) 4x + 9(x + 1) + 4 = 13 - 2x
A) Identity; {all real numbers}
C) Conditional; {0}

B) Conditional; {1}
D) Contradiction; ∅

32) 2

- r = -6 + 3(2 + 3r)
A) Conditional; {-3}
C) Conditional; {6}

30) ______

31) ______

32) ______
B) Identity; {all real numbers}
D) Contradiction; ∅

Solve the equation.
33)

33) ______

-3=1
A) {-24}

B) {24}

C) {12}

D) {-12}

34)

34) ______
=3
A) {-90}

B) {45}

C) {90}

D) {-45}

35)

35) ______
=3

A) {-21}

B) {24}

C) {21}

D) {-24}

36)

36) ______
=
A) {-12}

B) {3}

C) {4}

D) {-4}

37)

37) ______
= -4
A) {-13}

B) {13}

C) {-11}

D) {11}

38)

38) ______
+ 8 = 13
A) {-27}

B) {27}

C) {25}

D) {-25}

39)

39) ______
- 7 = -5
A) {22}

B) {24}

C) {-22}

D) {-24}

40)

40) ______
+

=-

A)

41) -0.07x + 0.11(x + 2200) = 250

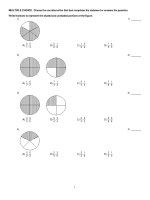
B)

C)

D)

41) ______


A) {20}

B) {200}

C) {20,000}

D) {2000}

42) 0.05y + 0.09(3000 - y) = 0.46y
A) {135}
B) {1350}

C) {1620}

D) {540}

43) -0.5(30,000) + 0.15p = 0.02(30,000 +p)
A) {120,000}
B) {2028}

C) {20,280}

D) {1,200,000}

Provide an appropriate response.
44) 2x - 5 = 5 + 7x - 3
Is this a linear equation?
A) Yes

42) ______

43) ______

44) ______
B) No

45)

45) ______
= 83
Is this a linear equation?
A) Yes

46) 5 - 7 = 3x

Is this a linear equation?
A) Yes

B) No
46) ______
B) No

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
47) If one step in the solution of an equation is -16 = -22, what is the final solution of the
47) _____________
equation?
48) True or false? This pair of equations is equivalent.

48) _____________

and

49) True or false? The solution set of the equation 7y - 6 = 7y + 3 is {0}. Explain.

49) _____________

50) True or false? The solution set of the equation 3(6s - 4) = 18s - 12 is {1}. Explain.

50) _____________

51) Find all values of s that make this statement true:

51) _____________

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.

Solve the equation for the specified variable. Use the distributive property to factor as necessary.
52) -5k + ar = r - 6y for r
52) ______
A)
B)
r=

or r =

C)

r=

or r =

D)
r=

or r =

53) -6s + 5p = tp - 5 for p
A)
p=

r=

53) ______
B)

or p =

C)

or r =

p=

or p =

p=

or p =

D)
p=

or p =

54)

54) ______
w=

for y


A)

B)
y=

or y =

C)

y=

or y =

y=

or y =

D)
y=

or y =

55)

55) ______
c=
A)

for t
B)
t=

or t =

C)

t=

or t =

t=

or t =

D)
t=

or t =

Solve the equation for y.
56) 8x + 2y = 5
A)

56) ______
B)

y=

y=

57) - 8x + 5y = 9
A)

y=

57) ______
C) y = 40x + 45

B)

y=

y=

58) 5x - 2y = 3
A)
y=

D) y = - 16x + 10

C)

D)
y=
58) ______

B)
, or y =

C)

y=

, or y =

D)
y=

, or y =

59) - 2x - 2y = 3
A)
y=

y=

, or y =
59) ______

B)
, or y =

C)

y=

, or y =

y=

, or y =

D)
y=

, or y =

Solve the problem.
60) Find the corresponding Celsius temperature for a temperature of 147°F. Round to the nearest
tenth, if necessary.
A) 63.9°C
B) 207°C
C) 296.6°C
D) 78.1°C

60) ______

61) Find the corresponding Fahrenheit temperature for a temperature of 65°C. Round to the nearest
tenth, if necessary.
A) 53.9°F
B) 18.3°F
C) 174.6°F
D) 149°F

61) ______

62) What is the perimeter of a rectangle of length 35 ft and width 15 ft?
A) 85 ft
B) 100 ft
C) 200 ft

62) ______

63) What is the area of a square with side 2.9 cm?
A) 33.64

B) 8.41

D) 50 ft
63) ______

C) 5.8

D) 24


64) Find the area of a triangle with height 12 m and base 15 m.
A) 13.5
B) 360
C) 90

64) ______
D) 180

65) Find the surface area of a cylinder with a radius of 3 cm and a height of 40 cm. Use 3.14 for π.
A) 810.12
B) 772.44
C) 3014.4
D) 753.6

65) ______

66) Jay drove 400 km at an average rate of 80 km/hr. How long did the trip take?
A) 6 hr
B)
C) 4 hr

D) 5 hr

66) ______

hr
67) Janet drove 248 km, and the trip took 4 hr. At what average rate was Janet traveling?
A) 992 km/hr
B)
C) 62 km/hr
D) 63 km/hr

67) ______

km/hr
68) The area of a trapezoid is 80 square feet. If the bases are 8 ft and 12 ft, find the altitude of the
trapezoid.
A) 16 ft
B) 1.5 ft
C) 4 ft
D) 8 ft

68) ______

69) A circle has a circumference of 24π m. Find the radius of the circle.
A) 6 m
B) 12 m
C) 4 m

69) ______
D) 24 m

70) Find the simple interest if $900 is borrowed at 12.1% for 6 months
A) $54.45
B) $217.80
C) $37.19

70) ______
D) $5445.00

71) Find the simple interest if $2800 is invested at 18.3% for 3.5 years.
A) $146.40
B) $512.40
C) $535.52

D) $1793.40

71) ______

72) Find the total amount in an account if $1500 is invested at 12% simple interest for 3.5 years.
A) $1680.00
B) $630.00
C) $2130.00
D) $1937.50

72) ______

73) Find the total amount that must be repaid if $900 is borrowed at 7% simple interest for 4.5 years.
A) $1478.57
B) $283.50
C) $1183.50

D) $963.00

73) ______

74) A chemical solution contains 9% salt. How much salt is in 3 ml of solution? Round your answer
to three decimal places, if necessary.
A) 0.27 ml
B) 3.333 ml
C) 33.333 ml
D) 2.7 ml

74) ______

75) During one year, the Larsons' real estate bill included $439 for local schools. Of this amount, $210
went to the high school district. What percent did the Larsons pay to the high school district?
Round your answer to two decimal places.
A) 22.90%
B) 47.61%
C) 47.84%
D) 52.16%

75) ______

76) A mixture of chlorine and water contains a total of 92 gallons of liquid. There are 63 gallons of
pure chlorine in the mixture. (i) What percent of the mixture is water? (ii) What percent of the
mixture is chlorine? Round your answer to the nearest percent, if necessary.
A) (i) 20% water; (ii) 80% chlorine
B) (i) 63% water; (ii) 37% chlorine
C) (i) 32% water; (ii) 68% chlorine
D) (i) 68% water; (ii) 32% chlorine

76) ______

77) The graph shows the percent of students at a local high school who were enrolled in a foreign
language class each school year during the 1980s.


77)

___
___

What is
the best
estimate
for the
number
of
students
taking a
language
in 1986 if
a total of
3460
students
were
enrolled
in the
school?
A) 51 students

B) 934 students

C) 2576 students

D) 2526 students

78) The graph shows the percent of students at a local high school who were enrolled in a foreign
language class each school year during the 1980s.

78) ______

What is the best estimate for the number of students not taking a language in 1984 if a total of
2840 students were enrolled in the school?
A) 1051 students
B) 4544 students
C) 1101 students
D) 1789 students
79) When a loan scheduled to run n payments is paid off k payments ahead of schedule, the amount

79) ______

of unearned interest u is given by u = f ∙
, where f is the total scheduled finance charge.
The finance charge on a loan taken out by Kathy is $744. If there were 24 equal monthly
installments needed to repay the loan, and the loan is paid in full with 14 months remaining,
find the amount of unearned interest. (Round your answer to the nearest cent.)
A) $136.40
B) $260.40
C) $245.30

D) $121.30
80) When a loan scheduled to run n payments is paid off k payments ahead of schedule, the amount
of unearned interest u is given by u = f ∙
, where f is the total scheduled finance charge.
The finance charge on a loan taken out by Kathy is $540. If there were 48 equal monthly
installments needed to repay the loan, and the loan is paid in full with 8 months remaining, find

the charge
tota paid.
l
(Round
fina your
nce answer


to the
nearest
cent.)

80)

___
___

A) $540.00

B) $376.53

C) $16.53

D) $523.47

81)

81) ______
The formula A =
gives the approximate annual interest rate for a consumer loan paid
off with monthly payments, where f is the finance charge on the loan, p is the number of
payments, and b is the original amount of the loan. Find the approximate annual interest rate for
an automobile loan to be repaid in 36 monthly installments if the finance charge on the loan is
$620 and the original loan balance is
necessary.)
A) 17.79%
B) 16.83%

(Round your answer to two decimal places, if
C) 15.87%

D) 17.29%

82) Students at East Central High School earned $880 selling pennants. They want to make $4560 for
a club trip. What percent of their goal has been reached? Round to the nearest tenth of a percent,
if necessary.
A) 52%
B) 1.9%
C) 19.3%
D) 5.2%

82) ______

83) Best Office Machines spent $19,040 this year on advertising alone. If total sales were $199,600,
what percent of total sales was spent on advertising? Round to the nearest tenth of a percent, if
necessary.
A) 10.5%
B) 1%
C) 105%
D) 9.5%

83) ______

84) A printer priced at $374 is sold for $326. What was the percent of price reduction? Round to the
nearest tenth of a percent, if necessary.
A) 12.8%
B) 114.7%
C) 87.2%
D) 779.2%

84) ______

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
Provide an appropriate response.
85) Suppose the formula A = 2πrh + 2π is solved for r with the following result: r =
85) _____________
. Is this an acceptable solution? Explain.
86)

86) _____________
Suppose the formula s =

g

+

t is solved for t with the following result:

. Is this an acceptable solution? Explain.
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
87)
87) ______
Which of the following is not a correct answer when the formula
A)
B)
C)

is solved for b?
D)

-B

88)

88) ______
Which of the following is not a correct answer when the formula

is solved for h?


A)

B)

C)

D)

3

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
89) The volume of a rectangular solid is to be 36 cubic units. Give two sets of possible
89) _____________
dimensions for the solid.
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
90) In order to purchase gutters for a roof, would you need to use perimeter or area to decide how
90) ______
much to buy?
A) Perimeter
B) Area
91) In order to purchase fabric for a tablecloth, would you need to use perimeter or area to decide
how much to buy?
A) Area
B) Perimeter
Translate the verbal phrase into a mathematical expression. Use x to represent the unknown number.
92) 120 more than a number
A) 120 - x
B) 120x
C) 120 + x
D) 120
93) 30 greater than a number
A) 30

B) x + 30

C) x - 30

D) 30x

94) 95 less than a number
A) x - 95

B) 95 - x

C) x + 95

D) 95x

95) 5 times a number
A) 5 + x

B) 5x

C) 5 - x

D)

96) A number divided by 55
A) 55 - x

B) 55 + x

C)

D) 55x

97) 262 divided by some number
A) 262x
B) 262 - x

C) 262 + x

D)

98) Four times a number added to 7
A) 4(x + 7)
B) 4x - 7

C) 4x(7 + x)

D) 4x + 7

99) The product of 5 and 2 less than a number
A) 5(x + 2)
B) 5(x - 2)

C) 5(2 - x)

D) 5x - 2

92) ______

93) ______

94) ______

95) ______

96) ______

97) ______

98) ______

99) ______

100) The product of 4 more than a number and 3 less than the number
A) (x + 4)(x - 3)
B) (x + 4)(3 - x)
C) (x + 4) - 3

D) x + 4(x - 3)

101) The quotient of 19 and ten times a nonzero number
A)
B)
C)

D)

(x ≠ 0)

91) ______

(x ≠ 0)

100) _____

101) _____
(x ≠ 0)

(x = 0)


Use the variable x for the unknown, and write an equation representing the verbal sentence. Then solve the problem.
102) Four times a number added to 7 times the number equals 55.
102) _____
A) 4(x + 7) = 55x; -5
B) 7x - 4x = 55; 5
C) 4x(7 + x) = 55; -5
D) 7x + 4x = 55; 5
103) When 3 times a number is subtracted from 7 times the number, the result is 36.
A) 3x(7 - x) = 36; -9
B) 3(x - 7) = 36x; 4
C) 7x - 3x = 36; 9
D) 3x + 9x = 36; 4

103) _____

104) If 4 times a number is added to -9, the result is equal to 13 times the number.
A) 4x + 9x = 13; 1
B) 13(4x - 9) = -9; -1
C) 4x - (-9) = 13x; 1

D) 4x + (-9) = 13x; -1

104) _____

105)

105) _____
When
A)

of a number is added to 24, the result is 28.
B)
+ x = 28; 28

x - 24 = 28; 208

C)

D)
28 +

x = 24; 16

24 +

x = 28; 16

106) When 50% of a number is subtracted from 70, the result is 2 less than the number.
A) 70 - 0.5x = x - 2; 48
B) 0.5x - 70 = x - 2; -136

C) 70 - 50 = x - 2; 22
D) 70 + 0.5x = x - 2; 144

106) _____

Decide whether the following is an expression or an equation. Simplify any expression or solve any equation.
107) 5x - (3x - 1) = 2
107) _____
A) Expression; 3x + 2
B)
Equation;
D) Expression; 2x + 3

C)
Equation;
108) 2(2x - 4) = 3(x + 3)
A) Equation; {-1}
C) Expression; 3x - 2

108) _____
B) Equation; {17}
D) Expression; 3x + 2

109) - 7(9x + 5) + 2(5x + 4)
A) Equation; {- 98}
C) Equation; {-53}

B) Expression; -53x - 27
D) Expression; 2x - 2

110) 2(x + 8) - 3(x - 2) = 0
A) Expression; 2x + 3
C) Equation; {10}

B) Equation; {22}
D) Expression; 2x - 2

109) _____

110) _____

111)

111) _____
xA)

x+

x-1
B)

Equation;

Equation;

C)

D)
Expression;

x-1

Expression;

x-1


112) -2(x + 2) + 8(x - 1) = 7
A) Expression; 6x - 19

112) _____
B)
Equation;
D) Expression; 6x + 5

C)
Equation;
113)

113) _____
x+
A)

x-

+1
B)

Expression;
C)

x+

Expression;

x+

D)
Equation;

Equation;

Solve the problem.
114) Find the length of a rectangular lot with a perimeter of 84 m if the length is 8 m more than the
width.
A) 17 m
B) 50 m
C) 25 m
D) 42 m

114) _____

115) A square plywood platform has a perimeter which is 8 times the length of a side, decreased by 8.
Find the length of a side.
A) 2
B) 1
C) 6
D) 4

115) _____

116) A rectangular Persian carpet has a perimeter of 168 inches. The length of the carpet is 24 in. more
than the width. What are the dimensions of the carpet?
A) Width: 54 in.; length: 78 in.
B) Width: 60 in.; length: 84 in.
C) Width: 72 in.; length: 96 in.
D) Width: 30 in.; length: 54 in.

116) _____

117) A pie-shaped (triangular) lake-front lot has a perimeter of 1400 ft. One side is 200 ft longer than
the shortest side, while the third side is 300 ft longer than the shortest side. Find the lengths of all
three sides.
A) 400 ft, 600 ft, 700 ft
B) 300 ft, 500 ft, 600 ft
C) 100 ft, 200 ft, 300 ft
D) 400 ft, 400 ft, 400 ft

117) _____

118) Gloria collected 27 fantail and comet goldfish. There were 7 fewer fantails than comets. How
many comets did Gloria have?
A) 20 comets
B) 12 comets
C) 17 comets
D) 10 comets

118) _____

119) The two largest oil spills together released 305 million gallons of oil into the oceans. The smaller

of the two released 81 million gallons less than the larger of the two. How many million gallons
of oil did the larger one release?
A) 224 million gallons
B) 137 million gallons
C) 193 million gallons
D) 112 million gallons

119) _____

120) A biologist collected 251 fern and moss samples. There were 79 fewer ferns than moss samples.
How many fern samples did the biologist collect?
A) 86 fern samples
B) 172 fern samples
C) 165 fern samples
D) 122 fern samples

120) _____

121) In a recent school board election, the two candidates for president received 2228 votes. The loser
received 1088 fewer votes than the winner. How many votes did the winner receive?

121) _____


A) 1658 votes

B) 1373 votes

C) 570 votes

D) 1140 votes

Solve the percent problem.
122) If Gloria received a 10 percent raise and is now making $27,500 a year, what was her salary
before the raise?
A) $25,000
B) $25,500
C) $26,500
D) $26,000

122) _____

123) Stevie bought a stereo for $290 and put it on sale at his store at a 50% markup rate. What was the
retail price of the stereo?
A) $390.00
B) $335.00
C) $435.00
D) $580.00

123) _____

124) An investor bought 100 shares of stock. The value of the shares went up 6% and then he sold

124) _____

them. How much did the investor pay for the 100 shares if he sold them for
A) $1500
B) $1450
C) $1629

D) $1487

125) At the end of the day, a storekeeper had $1590 in the cash register, counting both the sale of
goods and the sales tax of 6%. Find the amount that is the tax.
A) $85
B) $90
C) $80
D) $95

125) _____

126) After receiving a discount of 10.5% on its bulk order of typewriter ribbons, John's Office Supply
pays $5012. What was the price of the order before the discount?
A) $5600
B) $4486
C) $4736
D) $5538

126) _____

127) After spending $2850 for tables and $3650 for chairs, a convention center manager finds that 20%
of his original budget remains. Find the amount that remains. Round your answer to the nearest
dollar, if necessary.
A) $1625
B) $8125
C) $1300
D) $4563

127) _____

128) Midtown Antiques collects 6% sales tax on all sales. If total sales including tax are $1261.77, find
the portion that is the tax. Round your answer to the nearest cent.
A) $61.42
B) $75.71
C) $71.42
D) $1190.35

128) _____

Solve the investment problem.
129) Mardi received an inheritance of $60,000. She invested part at 11% and deposited the remainder
in tax-free bonds at 7%. Her total annual income from the investments was $5400. Find the
amount invested at 11%.
A) $29,000
B) $30,000
C) $15,000
D) $54,600

129) _____

130) Walt made an extra $5000 last year from a part-time job. He invested part of the money at 7%
and the rest at 6%. He made a total of $310 in interest. How much was invested at 6%?
A) $2500
B) $4000
C) $3000
D) $1000

130) _____

131) Roberto invested some money at 6%, and then invested $4000 more than twice this amount at

10%. His total annual income from the two investments was $3520. How much was invested at
10%?
A) $28,000
B) $24,000
C) $2800
D) $12,000

131) _____

Solve the mixture problem.
132) It is necessary to have a 40% antifreeze solution in the radiator of a certain car. The radiator now
has 70 liters of 20% solution. How many liters of this should be drained and replaced with 100%
antifreeze to get the desired strength?
A) 28 liters
B) 17.5 liters
C) 35 liters
D) 23.3 liters

132) _____


133) How many liters of a 60% alcohol solution must be mixed with 90 liters of a 80% solution to get a
70% solution?
A) 180 liters
B) 18 liters
C) 9 liters
D) 90 liters

133) _____

134) In a chemistry class, 3 liters of a 4% silver iodide solution must be mixed with a 10% solution to
get a 6% solution. How many liters of the 10% solution are needed?
A) 0.5 liters
B) 2.5 liters
C) 3 liters
D) 1.5 liters

134) _____

135) A merchant has coffee worth $4 a pound that she wishes to mix with 60 pounds of coffee worth
$9 a pound to get a mixture worth $5 a pound. How many pounds of the $4 coffee should be
used?
A) 240 lb
B) 150 lb
C) 300 lb
D) 120 lb

135) _____

Solve the problem.
136) Jay drove 308 kilometers at the average rate of 77 kilometers per hour. How long did the trip
take?
A) 3 hours
B) 4 hours
C) 2 hours
D) 5 hours

136) _____

137) Janet drove 252 kilometers and the trip took 4 hours. How fast was Janet traveling?

A) 63 kilometers per hour
B) 83 kilometers per hour
C) 73 kilometers per hour
D) 53 kilometers per hour

137) _____

138) What amount of money is found in a coin purse containing 13 dimes and 9 quarters?
A) $3.55
B) $355.00
C) $0.22
D) $4.15

138) _____

139) An equilateral triangle has perimeter 57 inches. What would be the perimeter of a square whose
sides each measure the same length as the side of the triangle?

139) _____

A) 19 inches

B) 76 inches

C) 38 inches

D) 361 inches

140) A convention manager finds that she has $1320, made up of twenties and fifties. She has a total
of 39 bills. How many fifty-dollar bills does the manager have?

A) 18
B) 12
C) 39
D) 21

140) _____

141) A woman has $1.70 in dimes and nickels. She has 5 more dimes than nickels. How many nickels
does she have?
A) 3
B) 13
C) 18
D) 8

141) _____

142) A bank teller has some five-dollar bills and some twenty-dollar bills. The teller has 5 more of the
twenties. The total value of the money is $775. Find the number of five-dollar bills that the teller
has.
A) 37
B) 27
C) 22
D) 32

142) _____

143) A cashier has a total of 123 bills, made up of fives and tens. The total value of the money is $915.
How many ten-dollar bills does the cashier have?
A) 30
B) 63

C) 90
D) 60

143) _____

144) There were 560 people at a play. The admission price was $2.00 for adults and $1.00 for children.
The admission receipts were $830. How many adults and children attended?
A) 145 adults and 415 children
B) 207 adults and 353 children
C) 270 adults and 290 children
D) 290 adults and 270 children

144) _____


145) There were 40,000 people at a ball game in Los Angeles. The day's receipts were $298,000. How
many people paid $12.00 for reserved seats and how many paid $5.00 for general admission?
A) 15,500 paid $12 and 24,500 paid $5
B) 24,500 paid $12 and 15,500 paid $5
C) 14,000 paid $12 and 26,000 paid $5
D) 26,000 paid $12 and 14,000 paid $5

145) _____

146) Jill is 20 kilometers away from Joe. Both begin to walk toward each other at the same time. Jill
walks at 2 kilometers per hour. They meet in 4 hours. How fast is Joe walking?
A) 2 kilometers per hour
B) 4 kilometers per hour
C) 3 kilometers per hour
D) 5 kilometers per hour

146) _____

147) Bert is 30 kilometers away from Brenda. Both begin to walk toward each other at the same time.
Bert walks at 4.5 kilometers per hour. They meet in 5 hours. How fast is Brenda walking?
A) 4.5 kilometers per hour
B) 1.5 kilometers per hour
C) 3.5 kilometers per hour
D) 2.5 kilometers per hour

147) _____

148) Candy and Delvis are riding bicycles in the same direction. Candy is traveling at a speed of 4
miles per hour, and Delvis is traveling at a speed of 6 miles per hour. In 4 hours what is the
distance between them (assuming that they began at the same point and time)?
A) 5 miles
B) 9 miles
C) 8 miles
D) 17 miles

148) _____

149) From a point on a river, two boats are driven in opposite directions, one at 8 miles per hour and
the other at 5 miles per hour. In how many hours will they be 39 miles apart?
A) 5 hours
B) 1 hour
C) 3 hours
D) 4 hours

149) _____

150) The speed of a stream is 5 mph. If a boat travels 54 miles downstream in the same time that it
takes to travel 27 miles upstream, what is the speed of the boat in still water?
A) 15 mph
B) 10 mph
C) 18 mph
D) 17 mph

150) _____

151) A plane flies 440 miles with the wind and 340 miles against the wind in the same length of time.
If the speed of the wind is 20 mph, what is the speed of the plane in still air?
A) 181 mph
B) 146 mph
C) 156 mph
D) 161 mph

151) _____

152) Tom Quig traveled 260 miles east of St. Louis. For most of the trip he averaged 60 mph, but for
one period of time he was slowed to 20 mph due to a major accident. If the total time of travel
was 7 hours, how many miles did he drive at the reduced speed?
A) 90 miles
B) 75 miles
C) 100 miles
D) 80 miles

152) _____

153) Find the measures of the supplementary angles.

153) _____

A) 43°, 47°

B) 133°, 47°

C) 47°, 43°

D) 137°, 43°

154) Find the measures of the complementary angles.

A) 43°, 47°

B) 36°, 54°

155) Find the measure of each angle in the triangle.

154) _____

C) 36°, 144°

D) 39°, 51°


155)

A) 28°, 128°, 24°

____
_

B) 38°, 123°, 19°

C) 32°, 37°, 21°

D) 34°, 125°, 21°

156) Find the measures of the supplementary angles.

A) 101.25°, 78.75°

B) 90°, 70°

156) _____

C) 96.25°, 83.75°

D) 98.25°, 81.75°

157) Find the measures of the complementary angles.

A) 150°, 30°

B) 37.5°, 7.5°

157) _____

C) 70°, 20°

D) 75°, 15°

158) Find the measures of the complementary angles.

A) 40°, 50°

B) 80°, 100°

158) _____

C) 42°, 48°

D) 45°, 45°

159) Find the measures of the vertical angles.

A) 82°, 82°

B) 14°, 14°

159) _____

C) 46°, 46°

D) 4°, 4°

160) Find the measure of each angle in the triangle.

A) 60°, 7°, 23°

B) 80°, 96°, 16°

160) _____

C) 60°, 97°, 23°

Solve the problem involving consecutive integers.
161) The sum of three consecutive even integers is 198. Find the integers.

D) 30°, 97°, 23°

161) _____


A) 68, 70, 72

B) 64, 66, 68

C) 59, 60, 61

162) The sum of two consecutive integers is -323. Find the larger integer.
A) -161
B) -162
C) -160

D) 66, 68, 70
162) _____
D) -163

163) Two pages that face each other in a book have 385 as the sum of their page numbers. What is the
number of the page that comes first?
A) 190
B) 193
C) 191
D) 192

163) _____

164) If three times the smaller of two consecutive integers is added to four times the larger, the result
is 137. Find the smaller integer.
A) 20
B) 57
C) 19
D) 18

164) _____

165) If the first and third of three consecutive odd integers are added, the result is 87 less than five
times the second integer. Find the third integer.
A) 58
B) 27
C) 29
D) 31

165) _____

166) The sum of the page numbers on the facing pages of a book is 377. Find the larger page number.
A) 189
B) 199

C) 187
D) 184

166) _____

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
Provide an appropriate response.
167) When solving a "word problem" we set up an equation in x. Give an example where the
167) ____________
solution of the equation is not the answer to the problem.
168) Two angles are complementary. One of the angles is r. How do you express the other
angle?

168) ____________

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
169) Which two of the following equations do not correctly state the relationship between distance,
169) _____
rate and time?
(a)

=r

(c)
=d
A) (b) & (d)

(b) dr = t

(d)

=t
B) (a) & (c)

C) (a) & (d)

D) (b) & (c)

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
170) One student solved a problem involving money by using a denomination based on cents 170) ____________
and not on dollars. For example, she multiplied the number of nickels by 5 cents and not
by $0.05. Was she wrong?
171) If you are given the measure of one angle of a triangle, would you be able to provide the
measures of the two other angles?

171) ____________

172) Suppose you were to solve a problem involving motion, and the problem gave the rate
in miles per hour and the time in minutes. Would you be able to determine the distance
traveled? If so, how would you go about it?

172) ____________

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Write an inequality statement involving the letter x that describes the given graph or interval notation.


173) (-2, ∞)
A) x < -2

173) _____
B) x ≥ -2

C) x ≤ -2

D) x > -2

174)

174) _____

A) x > 2

B) x < 2

C) x ≤ 2

D) x ≥ 2

175)

175) _____

A) x < 2

B) x ≥ 2

C) x > 2

D) x ≤ 2

176) (-∞, -3)
A) x ≤ -3

B) x ≥ -3

C) x < -3

D) x > -3

177) (-5, -1)
A) -5 < x < -1

B) -5 ≤ x < -1

C) -5 < x ≤ -1

D) -5 ≤ x ≤ -1

176) _____

177) _____

178)

178) _____

A) 0 ≤ x ≤ 4
179) [-5, -1)
A) -5 ≤ x < -1

B) 0 ≤ x < 4

C) 0 < x < 4

D) 0 < x ≤ 4
179) _____

B) -5 < x ≤ -1

C) -5 < x < -1

Solve the inequality. Give the solution set in both interval and graph forms.
180) a + 12 < 8

D) -5 ≤ x ≤ -1

180) _____

A) (-∞, -4)

B) (-∞, -4]

C) (-4, ∞)

D) [-4, ∞)

181) -2 a + 5 > -3 a + 8

A) (3, ∞)

181) _____


B) (13, ∞)

C) (-∞, 13)

D) (-∞, 3)

182) -3 z - 9 ≤ -4 z + 3

182) _____

A) (-∞, 12]

B) [12, ∞)

C) (-3, ∞)

D) (-∞, -3)

183) -6 z + 5 ≥ -7 z + 13

183) _____

A) (-∞, 8]

B) (-6, ∞)

C) (-∞, -6)

D) [8, ∞)

184) 18 x + 48 > 6(2 x + 11)

184)


_____
A) (3, ∞)

B) (-∞, 18)

C) (-∞, 3)

D) (18, ∞)

185) -4(6 z + 10) < -28 z - 16

185) _____

A) (-∞, 6)

B) (-∞, -28)

C) (6, ∞)

D) (-28, ∞)

186)

186) _____
<

A)

B)

C)


D)

187)

187) _____
<-

A)

B)

C)

D)

188) 15(3x - 14) > 3(15x - 7)
A) (-∞, 0)

C) (0, ∞)

188) _____
B) (-∞, ∞)

D) ∅


189) 7x + 3(x - 6) > 10x - 6
A) (-∞, 0)

C) (-∞, ∞)

189) _____
B) (0, ∞)

D) ∅

190) -3 < x + 3 ≤ 1

190) _____

A) (-6, -2]

B) [0, 4)

C) [-6, -2)

D) (0, 4]

191) 0 < 5 x ≤ 20

191) _____

A) [0, 4]

B) (0, 4]

C) (0, 4)

D) [0, 4)

192) 15 < -5 x ≤ 35

192) _____

A) (3, 7]

B) (-7, -3]

C) [-7, -3)

D) [3, 7)

193) 7 < 2 b + 3 ≤ 15

193) _____

A) (2, 6]

B) [2, 6)

C) [2, 6]

D) (2, 6)

194) 8 < -2 x + 4 ≤ 16


194)

_____
A) [2, 6)

B) (-6, -2]

C) [-6, -2)

D) (2, 6]

195)

195) _____
6≤

≤9

A)

B)

C)

D)

,

196) 4 < 1 - 4x ≤ 12

196) _____

A)

B)

-

-

C)

D)

-

-

-

-

Solve the problem.
197) A salesperson has two job offers. Company A offers a weekly salary of $90 plus commission of
6% of sales. Company B offers a weekly salary of $180 plus commission of 3% of sales. What is
the amount of sales above which Company A's offer is the better of the two?
A) $1500
B) $3100
C) $6000
D) $3000
198) Company A rents copiers for a monthly charge of $120 plus 6 cents per copy. Company B rents
copiers for a monthly charge of $240 plus 3 cents per copy. What is the number of copies above

197) _____

whic Comp
h
any


A's
198)
charges
are the
higher of
the two?
A) 4000 copies

____
_

B) 8000 copies

C) 4100 copies

199) A car rental company has two rental rates. Rate 1 is

per day plus

D) 2000 copies
per mile. Rate 2 is

199) _____

per day plus
per mile. If you plan to rent for one day, how many miles would you
need to drive to pay less by taking Rate 2?
A) more than 800 miles
B) more than 350 miles
C) more than 1400 miles
D) more than 700 miles
200) Jim has gotten scores of 95 and 84 on his first two tests. What score must he get on his third test
to keep an average of 80 or greater?
A) At least 86.3
B) At least 60
C) At least 61
D) At least 89.5

200) _____

201) A bag of marbles has twice as many blue marbles as green marbles, and the bag has at least 9

marbles in it. At least how many green marbles does it have?
A) At least 6 green marbles
B) At least 5 green marbles
C) At least 3 green marbles
D) At least 4 green marbles

201) _____

202) Jon has 635 points in his math class. He must have 62% of the 1200 points possible by the end of
the term to receive credit for the class. What is the minimum number of additional points he
must earn by the end of the term to receive credit for the class?
A) 109 points
B) 565 points
C) 394 points
D) 744 points

202) _____

203) Correct Computers, Inc. finds that the cost to make x laptop computers is

203) _____

while the revenue produced from them is
(C and R are in dollars). What is the
smallest whole number of computers, x, that must be sold for the company to show a profit?
A) 121
B) 25
C) 1,321,059,852
D) 270,791,962
204) Fantastic Flags, Inc. finds that the cost to make x flags is

while the revenue

204) _____

produced from them is
(C and R are in dollars). What is the smallest whole number of
flags, x, that must be sold for the company to show a profit?
A) 891
B) 321,537
C) 693,843
D) 413
205) Behemoth Back Packs, Inc. finds that the cost to make x back packs is

while the

205) _____

revenue produced from them is
(C and R are in dollars). What is the smallest whole
number of back packs, x, that must be sold for the company to show a profit?
A) 56,640
B) 394
C) 1,359,360
D) 17
206) Pizzicato Pizza, Inc. finds that the cost to make x pizzas (with one topping) is

206) _____

while the revenue produced from them is

(C and R are in dollars). What is
the smallest whole number of pizzas, x, that must be sold for the company to show a profit?
A) 119
B) 19,500
C) 87
D) 14,300
207) Miraculous Music, Inc. finds that the cost to make x compact discs is

while the

revenue produced from them is
(C and R are in dollars). What is the smallest whole
number of compact discs, x, that must be sold for the company to show a profit?
A) 987
B) 221,850
C) 705
D) 310,590

207) _____


Answer the question or solve the problem.
208) True or False? If x < 3 then -5x < -15.
A) True

208) _____
B) False

209) True or False? If x > 6 then 7x > 42.
A) True

209) _____
B) False

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
210) Under what conditions must the inequality symbol be reversed when solving an
210) ____________
inequality?
211) In solving the inequality 3x ≤ -24, would you have to reverse the inequality symbol?
Explain why.

211) ____________

212) The three-part inequality a < x ≤ b means "a is less than x and x is less than or equal to
b". Which of these inequalities is not satisfied by any real number x?
(a) -5 < x ≤ -11
(b) -8 < x ≤ -7
(c) 0 < x ≤ 4
(d)-2 < x ≤ 6

212) ____________

213)

213) ____________
If a < b, is it always true that

214) If b < 0, is it true that

>

? Explain.
214) ____________

> b? Explain.

215) If a ≤ b, is it always true that a + 9 ≤ b + 9? Explain.

215) ____________

216) If a ≤ b, is it always true that -2a ≤ -2b? Explain.

216) ____________

217) If a ≤ b, is it always true that

217) ____________

≤

? Explain.

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Let A = {q, s, u, v, w, x, y, z}, B = {q, s, y, z},
218) A ∩ B
A) {v, x}
B) {q, s, u, v, w, y}

and

Specify the following set.
218) _____

C) {q, s, y, z} or B

219) A ∪ B
A) {s, u, w}
C) {q, s, u, v, w, x, y, z} or A

B) {s, u, v, w, x, z}
D) {v, x}

220) A ∩ D
A) {s, u, w}
C) {q, s, u, v, w, x, y}

B) {s} or D
D) {v, x}

221) C ∪ B
A) {q, s, v, w, x, y, z}
C) {s, u, v, w, x, z}
222) B ∩ C

D) {s, u, v, w, x, z}
219) _____

220) _____

221) _____

B) {q, s, u, v, w, x, y}
D) {s, u, w}
222) _____


A) {y, z}

B) {q, y, z}

223) B ∪ C
A) {q, s, v, w, x, y, z}
C) {q, w, y, z}

C) {q, w, y}

D) {q, s, w, y, z}
223) _____

B) {q, s, u, w, y, z}
D) {y, z}

224) C ∪ D
A) {w, y}

B) {w, y, z}

C) {s, v, w, x, y, z}

D) {s, u, w, y, z}

225) C ∩ D
A) {q, s, u, w, y, z}

B) ∅

C) {q, y, z}

D) {q, w, y}

224) _____

225) _____

226) C ∪ A
A) ∅
C) {q, s, u, v, x, y, z}

B) {s, t}
D) {q, s, u, v, w, x, y, z} or A

227) A ∩ ∅
A) {w, y}
C) {q, s, u, v, w, x, y, z} or A

B) ∅
D) {q, s, u, v, x, z}

Graph the union or intersection of the two sets, as requested.
228) Intersection

226) _____

227) _____

228) _____

A)

B)

C)

229) Intersection

A)

B)

C)

229) _____