Đề kiểm tra KS lần 1 môn toán lớp 12 năm 20172018 THPT lý thánh tông mã đề 002

SỞ GD & ĐT HÀ NỘI
TRƯỜNG THPT LÝ THÁNH TÔNG
....................*...................

ĐỀ KIỂM TRA KHẢO SÁT LẦN 1
MÔN :TOÁN 12
NĂM HỌC: 2017-2018
(Thời gian làm bài:35 phút)

MÃ ĐỀ THI:002

ĐIỂM
Họ và tên:.........................................................
Số báo danh
Phòng thi....................
A.Phần trắc nghiệm(4,0 điểm)

Câu 1: Cho hàm số y =

1+ x
. Mệnh đề nào sau đây đúng?
1− x

A.Hàm số nghịch biến trên khoảng
B. Hàm số đồng biến trên các khoảng ( −∞;1) và ( 1;+∞ )
C. Hàm số đồng biến trên khoảng ( −∞;1) và nghịch biến trên khoảng ( 1;+∞ )
D. Hàm số đồng biến trên khoảng ( −∞; +∞ )
Câu 2: Cho hàm số y = x3 − 3x 2 + 1 . Tích các giá trị cực đại và cực tiểu của đồ thị hàm
số bằng:
A.- 6
B. -3

C. 0
D. 3

x2 + 3
Câu 3: Tìm giá trị nhỏ nhất của hàm số y =
trên đoạn [ 2;4] .
x −1
A. 6

B. -2

C. 7

Câu 4: Đồ thị hàm số y =

A. 0

D.

19
3

x−2
có bao nhiêu đường tiệm cận?
x2 − 4

B. 3

C. 1

D. 2

Câu 5: Biết rằng đường thẳng y = −2 x + 2 cắt đồ thị hàm số
điểm duy nhất có tọa độ ( x0 ; y0 ) . Tìm y0 ?

A. 4

B. 0

C. 2

y = x3 + x 2 + 2 tại một

D. -1

Câu 6: Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất:
A.Năm mặt

B. Bốn mặt

C. Ba mặt

Mã đề thi 002 - Trang 1/1

D. Hai mặt


Câu 7: Khối đa diện đều loại { 5;3} có số mặt là:
A.12

B. 8

C. 6

D. 20

Câu 8: Thể tích của khối lăng trụ đứng tam giác có chiều cao bằng 3a, đáy là tam giác
đều cạnh 2a là:

A. a

3

3

B. 3a

3

3

C. 6a

3

3

3a 3 3
D.
4

Câu 9: Hàm số nào sau đây đồng biến trên ¡ ?

A. y=

2x − 1
x +1

B. y=

x3
− x2 − x + 1
3

C. y=

x3 2
−x + x−2
3

D. y=x 4 + 2 x 2 + 1

1 3
2
Câu 10: Tìm tất cả các giá trị của m để hàm số y = − x + mx + ( 3m + 2 ) x + 1 nghịch
3
biến trên ¡ ?
 m ≤ −2
A. 
 m ≥ −1

B. -2 ≤ m ≤ -1

 m < −2
C. 
 m > −1

D. -2
4
2
Câu 11: Hàm số f ( x ) = x − 6 x + 8 x + 1 có bao nhiêu cực trị?

A. 0

B. 1

C. 2

D. 3

Câu 12: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = x 1 − x 2 . Khi đó giá trị M – m bằng?

A. 1

B. 3

C. 2

Câu 13: Tìm m để hàm số y =
A. m ∉{ −1;1}

D. 4

mx − 1
có tiệm cận đứng?
x−m

B. m ≠ 1

C. m = −1

D. m = 1

Câu 14: Đồ thị hàm số y = x 3 − 3x cắt:
A. Đường thẳng y = 5 tại ba điểm

B. Trục hoành tại hai điểm

C. Đường thẳng y = -3 tại hai điểm

D. Đường thẳng y =

4
tại ba điểm
3

Câu 15: Tính tổng diện tích các mặt của một khối 20 mặt đều cạnh bằng 2?

A.10 3

B. 20 3

C. 20

D. 10

Câu 16: Khi độ dài cạnh của hình lập phương tăng thêm 2cm thì thể tích của nó tăng
thêm98cm3. Cạnh của hình lập phương đã cho là:
Mã đề thi 002 - Trang 2/2


A.4cm

B. 5cm

C. 6cm

D. 3cm

Câu 17: Cho hàm số y = x3 − 3x 2 − mx + 2 . Tìm tất cả các giá trị của m để hàm số đồng
biến trên khoảng ( 0;+∞ ) .

A. m ≤ -1

B. m ≤ 0

C. m ≤ -3

D. m ≤ −2

4
2
2
Câu 18: Tìm m để hàm số y = mx + ( m − 9 ) x + 1 có hai điểm cực đại và một điểm
cực tiểu.

A. -3
B. 0
 m < −3
D. 
0 < m < 3

C. m<-3

Câu 19. Một sợi dây kim loại dài 60cm được cắt thành hai đoạn. Đoạn thứ nhất được
uốn thành một hình vuông, đoạn thứ hai được uốn thành một vòng tròn. Hỏi khi tổng
diện tích của hình vuông và hình tròn ở trên là nhỏ nhất thì chiều dài đoạn dây uốn thành
hình vuông bằng bao nhiêu(làm tròn đến hàng phần trăm)?

A. 26,43cm

B. 33,61cm

C. 40,62cm

D. 30,54cm

3
2
Câu 20: Cho hàm số y = x + bx + cx + d ( c < 0 ) có đồ thị (T) là một trong bốn hình
dưới đây. Hỏi đồ thị (T) là hình nào?

A.Hình 1

B. Hình 2

C. Hình 3

D. Hình 4

--------- Hết ---------TRẢ LỜI PHẦN TRẮC NGHIỆM MÃ ĐỀ 001
Câu
Đáp
án
Câu
Đáp

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

án

Mã đề thi 002 - Trang 3/3


SỞ GD & ĐT HÀ NỘI
TRƯỜNG THPT LÝ THÁNH TÔNG
....................*...................

ĐỀ KIỂM TRA KHẢO SÁT LẦN 1
MÔN :TOÁN 12
NĂM HỌC: 2017-2018
(Thời gian làm bài:55 phút)

MÃ ĐỀ THI: 002

Họ và tên:.................................................................
Số báo danh:....................................................... Phòng thi....................
B.Phần tự luận (6,0 điểm)
Câu 1(2,0điểm). Cho hàm số y = x3 – 3x2 + 2

(C)

1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Tìm các giá trị của tham số m để phương trình: -x 3 + 3x2 + 2m = 0 có 3 nghiệm
phân biệt.
1 3
2
Câu2(1,0điểm).Viết phương trình tiếp tuyến của đồ thị hàm số y = − x + 3x + 2 x − 10

3
tại điểm có hoành độ bằng -3.
Câu 3(1,0điểm). Cho hai số thức x,y thuộc khoảng (-3;1) thỏa mãn điều kiện x+y=1.Tìm
giá trị lớn nhất của biểu thức P =

x 2 + y + 3x + 2
?
y2 + 2x

Câu 4(2,0 điểm). Cho khối chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 4a,
BC = 3a. Cạnh bên SA vuông góc với mặt đáy và cạnh SC = 7a
1. Tính thể tích khối chóp S.ABC theo a
1
2. Gọi M, N lần lượt thuộc SB và SC. Sao cho SM = 2 MB; SN = SC .Tính thể tích
3
khối chóp S.AMN

---------------------HẾT--------------------------

Mã đề thi 002 - Trang 4/4


ĐÁP ÁN MÃ ĐỀ 002 PHẦN TRẮC NGHIỆM(mỗi đáp án đúng 0,2 điểm)
1-B

2-B

3-A

4-D

5-C

6-D

7-A

8-B

9-C

10-B

11-B

12-A

13-A

14-D

15-B

16-D

17-C

18-C

19-B

20-A

ĐÁP ÁN MÃ ĐỀ 002 PHẦN TỰ LUẬN
I.

Phần tự luận (6,0 điểm)

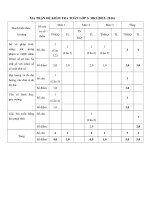
CÂU

NỘI DUNG

ĐIỂM

TXĐ: D = R
=-∞ ;

=+∞

0,25

y’ = 3x2 – 6x=0  x=0;x=2

BBT
−∞
x
y’
y

+

0
0

-

2
0

+∞

0,5

+

+∞

2

−∞

Câu 1
(2,0điểm
)

-2
ĐB: ( −∞;0 ) và ( 2; +∞ ) ;NB: (0;2)
xCĐ=0,yCĐ=2 ;xCT=2 ,yCT=-2

0,25

0,5

Đồ thị :
2.Tìm điều kiện của tham số m để phương trình -x3 + 3x2 + 2m = 0 có
3 nghiệm thực.
0,25
− x 3 + 3 x 2 + 2m = 0 ⇔ x 3 – 3 x 2 + 2 = 2 m + 2
Phương trình có 3 nghiệm thực −2 < 2m + 2 < 2 ⇔ −2 < m < 0

Viết phương trình tiếp tuyến của đồ thị hàm số
Câu 2
có hoành độ bằng -3
(1,0điểm) x = −3 ⇒ y = 20; y ' ( 3 ) = −25
0
0
Câu 3
(1,0điểm

)

1
y = − x 3 + 3x 2 + 2 x − 10
3

0,25
tại điểm

0,5
Pttt : y = −25 ( x + 3) + 20 = −25 x − 55

0,5
Cho hai số thức x,y thuộc khoảng (-3;1) thỏa mãn điều kiện x+y=1.Tìm giá trị
lớn nhất của biểu thức P =

x 2 + y + 3x + 2
?
y2 + 2x

Mã đề thi 002 - Trang 5/5


Ta có x + y = 1 ⇒ y = 1 − x ⇒ P =
Xét hàm số f ( x ) =

x2 + 2x + 3
x2 + 1

0,25

x2 + 2x + 3
; x ∈ ( −3;1)
x2 + 1

0,25

 x = −1 + 2
−2 x − 4 x + 2
f '( x) =
;
chof

'
x
=
0
⇔
(
)

( x 2 + 1) 2
 x = −1 − 2
2

Bảng biến thiên
x
-3
-1- 2
0
f’

-1 + 2
0
-

+

1

0,25

2+ 2

f(x)
2− 2

0,25

Tìm được:

Cho khối chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 4a,
BC = 3a. Cạnh bên SA vuông góc với mặt đáy và cạnh SC = 7a
1.Tính thể tích khối chóp S.ABC theo a.
AC = BC 2 − AB 2 =
SA = SC 2 − AC 2 =

( 3a )
( 7a )

2

2

+ ( 4a 2 ) = 5a

0,25

− ( 5a ) = 2a 6
2

1
1

AB.BC = 3a.4a = 6a 2
2
2
1
1
Câu 4
V = Bh = .6a 2 .2a 6 = 4 6a 3
3
3
(2,0 điểm)
B = S ABC =

0,25
0,5
1
3

2. Gọi M, N lần lượt thuộc SB và SC. Sao cho SM = 2MB; SN = SC .Tính thể
tích khối chóp S.AMN
VS . AMN SA SM SN 2
=
.
.
=
VS . ABC SA SB SC 9

0,5

2
2

8 6a 3
VS . AMN = .VS . ABC = .4 6.a 3 =
9
9
9

0,5

Mã đề thi 002 - Trang 6/6