2D1 2 143c44 DE SO 4 THPTQG năm 2018 đề chuẩn nâng cao 04 gv đặng việt hùng tuan vu

4
2
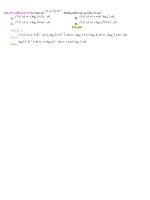
Câu 44. [2D1-2.14-3] Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số y  x  2mx  m  1 có ba điểm
cực trị tạo thành một tam giác có bán kính đường tròn ngoại tiếp chúng bằng 1?
A. 1.
B. 2.
C. 3.
D. 4.
Lời giải
Đáp án B
x0
�
y '  4 x 3  4mx  0 � �2
.
4
2
x m
y

x

2
mx

m

1,
�
Xét hàm số
có
Để hàm số có 3 điểm cực trị khi và chỉ khi m  0.

2
C  m ; m 2  m  1
A  0; m  1 , B m ;  m  m  1
Khi đó, gọi
và
là 3 điểm cực trị của ÐTHS .
H  0; m2  m  1 � AH  m2 .
Gọi H là trung điểm của BC suy ra
1
1
S ABC  . AH .BC  m 2 .2 m  m 2 m .
2
2
Diện tích tam giác ABC là
AB. AC.BC
S ABC 
� AB 2 .BC  4S ABC
4
4 RABC
Và AB  AC  m  m suy ra









�  m 4  m  .2 m  4m 2 m � m 4  2 m 2  m  0 � m  m3  2m  1  0.

Kết hợp với m  0 suy ra có 2 giá trị m cần tìm.