GT Đồ họa máy tính 3

Đ H A MÁY TÍNHỒ Ọ
Đ H A MÁY TÍNHỒ Ọ
2
CHƯƠNG III
ĐỒ HỌA BA CHIỀU
Bài 1 – Các phép biến đổi 3D 
Bài 2 – Biểu diễn các đối tượng 3D 
Bài 3 – Các thuật toán khử mặt khuất 
Bài 4 – Biểu diễn đường và mặt cong 
Bài 5 – Tô bóng các đối tượng 
3
Bài 1
CÁC PHÉP BIẾN ĐỔI 3D
I. Các phép biến đổi hình học cơ sở 
II. Phép biến đổi ngược 
III. Kết hợp các phép biến đổi 
4
Đại số véctơ
•
Biểu diễn véctơ
–
Đoạn thẳng có hướng giữa hai điểm xác định
•
Cộng hai véctơ
•
Nhân hai véctơ
–
Tích vô hướng hay tích điểm
–
Độ dài véctơ
V

P2
P1
V2=(x2,y2,z2)
V1+V2
V1=(x1,y1,z1)
z
x
y
V1
V2
θ
Chiếu V2 trên V1
1 2 1 2 1 2 1 2
( , , )x x y y z z+ = + + +V V
1 2 1 2 1 2 1 2
. x x y y z z= + +V V
1 2 1 2
. cos
θ
=V V V V
2 2 2
( )x y z= = + +V V.V
5
Đại số véctơ
•
Tích có hướng của hai véctơ
–
Kết quả là véctơ vuông góc với mặt
phẳng tạo ra bởi hai véctơ
–

Véctơ đơn vị u
•
Có độ dài bằng 1
•
Xác định hướng của véctơ kết quả
–
Quy tắc bàn tay phải
•
Nắm tay phải, để cong các ngón tay
từ A đến B (nếu AxB), lòng bàn
tay hướng về gốc, ngón cái sẽ trỏ theo
hướng của u
•
Véctơ kết quả
V1
V2
θ
V1 x V2
u
sinAxB A B
θ
= u
6
Bài 1 – CÁC PHÉP BIẾN ĐỔI 3D
Hệ toạ độ thuần nhất
Trong hệ toạ độ thuần nhất, mỗi điểm (x, y, z) trong hệ toạ độ
Descartes được biểu diễn bởi bộ 4 toạ độ không gian (hx, hy, hz, h). Để
tiện lợi, cho h=1. Như vậy, một điểm (x, y, z) trong hệ toạ độ Descartes
sẽ biến thành điểm (x, y, z, 1) trong hệ toạ độ thuần nhất. Còn điểm (x, y,
z, w) trong hệ toạ độ thuần nhất (với w≠0) sẽ ứng với điểm (x/w, y/w,

z/w) trong hệ toạ độ Descartes.
Xét trong hệ toạ độ thuần nhất, phép biến đổi affine 3D biến điểm
P(x,y,z,1) thành điểm Q(x’, y’, z’,1) có dạng:
Q=P.M
Trong đó, ma trận biến đổi M có dạng:
Tònh tiến
Quay , tỉ lệ, biến dạng
0
0
0
1
x y z
a b c
d e f
M
g h i
tr tr tr
 
 ÷
 ÷
=
 ÷
 ÷
 ÷
 
7
Một số tính chất của các phép biến đổi 3 chiều

Tính chất đường thẳng được bảo toàn. Nghóa là
một đường thẳng trong không gian 3 chiều khi biến

đổi sẽ thành một đường thẳng.

Tính chất song song được bảo toàn: hai đường
thẳng song song khi biến đổi cũng sẽ thành 2 đường
thẳng song song.

Tính tỉ lệ về khoảng cách được bảo toàn: ảnh
của một điểm P chia đoạn thẳng AB theo tỉ lệ f, sẽ
chia đoạn thẳng A’B’ theo tỉ lệ f, với A’B’ là ảnh
của đoạn thẳng AB.
8
I. Các phép biến đổi hình học cơ sở
1. Phép tònh tiến (translation)
Trong phép biến đổi tònh tiến 3D, mỗi điểm được dòch đi
một khoảng là t
x
, t
y
, t
z
theo ba trục toạ độ.
Ma trận của phép biến đổi tònh tiến là:

x
y
z
P(x,y,z)
Q(x’,y’,z’)
tr=(tr
x

,tr
y
,tr
z
)
1 0 0 0
0 1 0 0
0 0 1 0
1
x y z
M
t t t
 
 ÷
 ÷
=
 ÷
 ÷
 ÷
 
9
I. Các phép biến đổi hình học cơ sở
2. Phép đối xứng
Đối xứng qua mặt phẳng xy:
Đối xứng qua mặt phẳng xz:
Đối xứng qua mặt phẳng yz:
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

M
 
 ÷
 ÷
=
 ÷
−
 ÷
 ÷
 
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
M
 
 ÷
−
 ÷
=
 ÷
 ÷
 ÷
 
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
M
−

 
 ÷
 ÷
=
 ÷
 ÷
 ÷
 
10
I.Các phép biến đổi hình học cơ sở
2.Phép đối xứng
Đối xứng qua qua gốc tọa độ:
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
M
−
 
 
−
 
=
 
−
 
 
11
I.Các phép biến đổi hình học cơ sở
3. Phép biến đổi tỉ lệ (scaling)

Phép biến đổi tỉ lệ trong không gian 3D là sự mở rộng của phép biến
đổi tỉ lệ trong không gian 2D. Ma trận của phép biến đổi tỉ lệ là:

s
x
, s
y
, s
z
là các hệ số tỉ lệ
Khi s
x
= s
y
= s
z
=s ta có phép biến đổi đồng dạng.
Trong phép biến đổi trên, gốc toạ độ O sẽ có ảnh là chính nó. Khí
đó O là tâm của phép biến đổi.
y
x
z
0 0 0
0 0 0
0 0 0
0 0 0 1
x
y
z
s

s
M
s
 
 ÷
 ÷
=
 ÷
 ÷
 ÷
 
12
3. Phép biến đổi tỉ lệ (scaling)
Phép biến đổi tỉ lệ theo một tâm (x
0
, y
0
, z
0
) bất kỳ được mô tả bằng
một dãy ba phép biến đổi sau:
Tònh tiến tâm (x
0
, y
0
, z
0
) về gốc toạ độ.
Biến đổi tỉ lệ có tâm ở gốc toạ độ.
Tònh tiến ngược tâm từ gốc toạ độ về lại vò trí ban đầu.

Kết hợp ba bước biến đổi trên, ta được ma trận của phép biến đổi theo
tâm (x
0
, y
0
, z
0
) như sau:
0 0 0 0 0 0
1 0 0 0 1 0 0 0
0 0 0
0 1 0 0 0 1 0 0
0 0 0
0 0 1 0 0 0 1 0
0 0 0
1 1
0 0 0 1
x
y
z
s
s
M
s
x y z x y z
   
 
 ÷  ÷
 ÷
 ÷  ÷

 ÷
= × ×
 ÷  ÷
 ÷
 ÷  ÷
 ÷
 ÷
 ÷  ÷
− − −
 
   
0 0 0
0 0 0
0 0 0
0 0 0
(1 ) (1 ) (1 ) 1
x
y
z
x y z
s
s
M
s
s x s y s z
 
 ÷
 ÷
=
 ÷

 ÷
 ÷
− − −
 
13
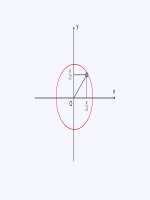
4. Pheựp quay (rotation)
a. Quay quanh moọt truùc toaù ủoọ

Qui c: Quay ngc chiu kim ng h theo trc s to thnh gúc
dng nu nhỡn v gc ta t na trc dng.
Quay quanh trc z
z
z
x
y
' cos sin
' sin cos
'
x x y
y x y
z z


=
= +
=
[ ] [ ]
cos sin 0 0
sin cos 0 0
' ' ' 1 1

0 0 1 0
0 0 0 1
x y z x y z






=



14
4. Phép quay (rotation)
a. Quay quanh một trục toạ độ
Các ma trận biểu diễn phép quay quanh trục x, y, z một góc α lần
lượt là R(x, α), R(y, α), R(z, α) như sau:
Quay quanh trục x:
Quay quanh trục y:
Quay quanh trục z:
1 0 0 0
0 cos sin 0
( , )
0 sin cos 0
0 0 0 1
R x
α α
α
α α

 
 ÷
 ÷
=
 ÷
−
 ÷
 ÷
 
cos 0 sin 0
0 1 0 0
( , )
sin 0 cos 0
0 0 0 1
R y
α α
α
α α
−
 
 ÷
 ÷
=
 ÷
 ÷
 ÷
 
cos sin 0 0
sin cos 0 0
( , )

0 0 1 0
0 0 0 1
R z
α α
α α
α
 
 ÷
−
 ÷
=
 ÷
 ÷
 ÷
 
15
4. Phép quay (rotation)
b.Quay quanh một trục bất kỳ.
Giả sử trục quay được biểu diễn bởi
đường thẳng k đi qua 2 điểm P
0
và P
1
.
Quay điểm P(x,y,z) một góc α sẽ
biến thành điểm Q(x’, y’, z’). Để thực hiện
phép quay quanh k, ta thực hiện một chuỗi các thao tác sau:
- Thực hiện một số phép tònh tiến, quay để k trùng trục z như sau:
+ Tònh tiến k về gốc toạ độ (thành trục k’) với ma trận biến đổi là Tr(-P
0

).
+ Quay quanh trục x một góc ϕ để đặït k’lên mặt phẳng Oxz (thành trục k’’)
với ma trận biến đổi là: R(x, ϕ) .
+ Quay quanh trục y một góc θ để đưa k’’ về trục z với mt biến đổi là: R(y,-θ).
- Quay quanh trục z một góc α với ma trận biến đổi là: R(z, α).
- Thực hiện ngược lại các phép biến đổi sao cho k trở về vò trí ban đầu với các ma
trận biến đổi lần lượt là: R(y,θ), R(x,-ϕ), Tr(P
0
).
y
x
z
k
P
0
P
1
k’
k’’
k
z
k
y
k
x
d
ϕ
φ
16
4. Phép quay (rotation)

b.Quay quanh một trục bất kỳ.
Vậy phép quay một điểm quanh
trục k bất kỳ với một góc α được
phân tích thành các chuỗi biến đổi sau:
Tr(-P
0
).R(x, ϕ).R(y,-θ). R(z, α).R(y,θ), R(x, -ϕ), Tr(P
0
).
Trong đó góc quay ϕ, θ được xác đònh dựa trên cơ sở chiếu k’ lên mặt
phẳng yz, ta có:
k=P
0
P
1
;
cos(ϕ)=k
z
/d ; sin(ϕ)=k
y
/d
cos(θ)=k
z
/k ; sin(θ)=k
x
/k
y
x
z
k

P
0
P
1
k’
k’’
k
z
k
y
k
x
d
ϕ
φ
2 2
y z
d k k= +
17
II. Phép biến đổi ngược
Tất cả các phép biến đổi ở trên đều có ma trận nghòch đảo.
- Ma trận nghòch đảo của phép tònh tiến có được bằng cách
thay các hệ số t
x
, t
y
, t
z
bằng -t
x

, -t
y
, -t
z
.
- Ma trận nghòch đảo của phép biến đổi tỉ lệ có được bằng
cách thay các hệ số s
x
, s
y
, s
z
bằng 1/s
x
, 1/s
y
, 1/s
z

- Ma trận nghòch đảo của phép quay có được bằng cách
thay góc α bằng -α.
18
III. Kết hợp các phép biến đổi
Để kết hợp các phép biến đổi affine 3D, ta thực hiện
tương tự như ở phép biến đổi 2D bằng cách sử dụng hệ toạ độ
thuần nhất. Bằng cách này, ta cũng có kết quả tương tự như trong
trường hợp biến đổi 2D.
Nếu M
1
bến đổi P thành P’và M

2
biến đổi P’ thành Q thì
M=M
1
M
2
sẽ biến đổi P thành Q.
Như vậy ma trận của phép biến đổi kết hợp có thể được
tính từ tích các ma trận của các phép biến đổi thành phần.
19
Bài 2
BIỂU DIỄN CÁC ĐỐI TƯNG 3D
I. Mô hình khung kết nối 
II. Mô hình các mặt đa giác 
III. Chiếu vật thể trong không gian lên mặt phẳng 
IV. Quan sát vật thể 3D và Quay hệ quan sát 
20
I. Mô hình khung kết nối (WF-WireFrame model)
Một mô hình khung kết nối gồm: tập các đỉnh và tập các
cạnh nối giữa các đỉnh đó. Khi thể hiện bằng mô hình này, các
đối tượng ba chiều có vẻ rỗng và không thực tế lắm. Để hoàn
thiện hơn, người ta dùng kỹ thuật tạo bóng, loại bỏ các đường và
mặt khuất. Tuy nhiên vẽ bằng mô hình này thường nhanh nên nó
thường được dùng trong việc xem phác thảo (preview) các đối
tượng, đặc biệt là trong các hệ CAD.
Mô hình khung nối kết thể hiện hình dáng của một đối tượng 3D
bởi 2 danh sách:
Danh sách các đỉnh (vertices): lưu toạ độ các đỉnh.
Danh sách các cạnh (edges) nối giữa các đỉnh đó: lưu 2 đỉnh
đầu và cuối của từng cạnh.

21
I. Mô hình khung kết nối (WF-WireFrame model)
Danh sách các đỉnh Danh sách các
cạnh
Đỉnh x y z Cạnh Đầu Cuối
1 0 0 0 1 1 2
2 0 1 0 2 2 3
3 0 1 1 3 3 4
4 0 0.5 1.5 4 4 5
5 0 0 1 5 5 1
6 1 0 0 6 6 7
7 1 1 0 7 7 8
8 1 1 1 8 8 9
9 1 0.5 1.5 9 9 10
10 1 0 1 10 10 6
11 1 6
12 2 7
13 3 8
14 4 9
15 5 10
16 2 5
17 1 3
Ví dụ: biểu diễn một căn nhà thô sơ
z
x
y
1
2
3
4

5
6
7
9
10
1
1
1
8
22
I. Moâ hình khung keát noái (WF-WireFrame model)
Danh sách đỉnh Danh sách cạnh
Đỉnh X Y Z Cạnh Đầu Cuối
1 1 1 -3 1 1 5
2 -1 1 -3 2 2 6
3 -1 -1 -3 3 3 12
4 1 -1 -3 4 4 11
5 1 1 0 5 5 6
6 -1 1 0 6 6 7
7 -1 -1 0 7 7 8
8 1 -1 0 8 8 5
9 1 -1 2 9 9 10
10 -1 -1 2 10 11 12
11 1 -1 3

12 -1 -1 3

 

1

1
Y
X
Z
(1,1,-3)
(-1,1,-3)
(-1,-1,-3)
(1,-1,-3)
(1,-1,3)
(1,-1,2)
(-1,-1,3)
(-1,-1,2)
(1,-1,0)
(-1,1,0) (-1,-1,0)
(1,1,0)
1
23
4
5
67
8
9
11
12
10
Ví dụ: lưu trữ hình dáng một chiếc ghế gỗ thô sơ
23
I. Mô hình khung kết nối (WF-WireFrame model)
Có nhiều cách để lưu trữ một mô hình WF trên máy tính. Ở
đây ta dùng cấu trúc mảng các record như sau:

#define MaxDinh 50 //so dinh toi da co the bieu dien
#define MaxCanh 100 //so canh toi da
typedef struct{
float x, y, z;
} diem3D;
typedef struct{
int sodinh; // số đỉnh trong mô hình
int socanh; // số cạnh trong mô hình
diem3D dinh[maxdinh];
int canh[maxcanh][2];
}wireframe;
24
II. Mô hình các mặt đa giác ( Polygon Mesh model)
Mơ hình các mặt đa giác: vật thể 3D được xác định thơng qua
các mặt, mỗi mặt lại được xác định thơng qua các đỉnh của mặt đa giác.
Với mơ hình các mặt đa giác, chúng ta khơng chỉ tạo ra được hình dáng
của vật thể như mơ hình Wireframe mà còn thể hiện được các đặc tính
về màu sắc và nhiều tính chất khác của vật thể. Song để có thể mơ tả
vật thể 3D một cách trung thực thì đòi hỏi người lập trình phải tính
tốn và giả lập nhiều thơng tin, mà mấu chốt là vấn đề khử mặt khuất
và chiếu sáng.

Mô hình các mặt đa giác thể hiện hình dáng của một đối
tượng 3D bởi 2 danh sách:
Danh sách các đỉnh: lưu toạ độ các đỉnh.
Danh sách các mặt: lưu thứ tự các đỉnh tạo nên mặt đó.
25
II.Moâ hình caùc maët ña giaùc ( Polygon Mesh model)
Ví dụ: Mô tả vật thể như trong hình vẽ sau:
Danh sách đỉnh Danh sách mặt

Đỉnh X Y Z mặt
1 x1 y1 z1 1 1,3,2
2 x2 y2 z2 2 4,5,6
3 x3 y3 z3 3 1,4,6,3
4 x4 y4 z4 4 3,6,5,2
5 x5 y5 z5 5 1,2,5,4
6 x6 y6 z6
1
2
3
4
5
6
M t 3ặ
M t 1ặ
M t 4ặ
M t 5ặ
M t 2ặ