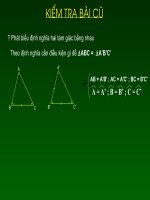Truong hop bang nhau ccc

<span class='text_page_counter'>(1)</span>Le Thi Phu.

<span class='text_page_counter'>(2)</span> ? Phát biểu định nghĩa hai tam giác bằng nhau Vận dụng: Điền vào chỗ trống(...) để được khẳng định đúng A’. A.  ABC =  A'B'C'. ˆ. . ˆ ˆ. ˆ ˆ. ˆ. A  A ;B B;C C ………………………………… AB A’B’ ; AC = A'C' ; BC = B'C' ....=..... B. C. C’. B’. Quan s¸t h×nh vÏ sau vµ cho biÕt:Hai tam gi¸c MNP vµ tam gi¸c M’N’P’ cã nh÷ng yÕu tè nµo b»ng nhau? M. MNP và M'N'P'. M'. Có MN = M'N' MP = M'P' NP = N'P' N. Le Thi Phu. P. N'. P'. thì MNP ? M'N'P'.

<span class='text_page_counter'>(3)</span> Le Thi Phu.

<span class='text_page_counter'>(4)</span> T. TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm. •VÏ ®o¹n th¼ng BC=4cm. Le Thi Phu.

<span class='text_page_counter'>(5)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm. •VÏ ®o¹n th¼ng BC=4cm. Le Thi Phu.

<span class='text_page_counter'>(6)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm. B. Le Thi Phu. C. •Trªn cïng mét nöa mÆt ph¼ng bê BC , VÏ cung trßn t©m B, b¸n kÝnh 2cm..

<span class='text_page_counter'>(7)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm. B. Le Thi Phu. C. •Trªn cïng mét nöa mÆt ph¼ng bê BC , VÏ cung trßn t©m B, b¸n kÝnh 2cm..

<span class='text_page_counter'>(8)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm. B. Le Thi Phu. C. •Trªn cïng mét nöa mÆt ph¼ng bê BC , VÏ cung trßn t©m C, b¸n kÝnh 3cm..

<span class='text_page_counter'>(9)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm. B. C. •VÏ cung trßn t©m C, b¸n kÝnh 3cm. Le Thi Phu.

<span class='text_page_counter'>(10)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm A B. Le Thi Phu. C. •Hai cung trªn c¾t nhaut¹i A. •VÏ ®o¹n th¼ng AB, AC, ta cã tam gi¸c ABC.

<span class='text_page_counter'>(11)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm A B. C. •Hai cung trßn trªnc¾t nhau t¹i A. •VÏ ®o¹n th¼ng AB, AC, ta cã tam gi¸c ABC. Le Thi Phu.

<span class='text_page_counter'>(12)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm A B. C. •Hai cung trßn trªnc¾t nhau t¹i A. •VÏ ®o¹n th¼ng AB, AC, ta cã tam gi¸c ABC. Le Thi Phu.

<span class='text_page_counter'>(13)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm A. B C •VÏ ®o¹n th¼ng BC=4cm. •Trªn cïng mét nöa mÆt ph¼ng bê BC, vÏ cung trßn t©m B, b¸n kÝnh 2cm. •VÏ cung trßn t©m C, b¸n kÝnh 3cm. •Hai cung trßn trªn c¾t nhau t¹i A. Le Thi Phu •VÏ ®o¹n th¼ng AB, AC, ta cã tam gi¸c ABC.

<span class='text_page_counter'>(14)</span> Bµi to¸n: VÏ tam gi¸c A’B’C’biÕt : B’C’= 4cm, A’B’=2cm, A’C’= 3cm. A’. A B. Le Thi Phu. C. B’. C’.

<span class='text_page_counter'>(15)</span> §o vµ nhËn xÐt c¸c gãc A vµ gãc A’ , gãc B vµ gãc B’, gãc C vµ gãc C’. C. 180 170 160 150 0 10 2 0 30 140 40. 50 40 30 2 0 60 10 130 140 150 1 70 0 6 2 0 1 170 0 18 110 80 0 0 10. HS 1. Le Thi Phu. 10 0 20 170180 30 160 150. 10 0 20 180 30 160 170 150. 0 14. B. A’. 0 14. 40. 180 170 160 150 0 10 2 0 14 30 0 40. A. 40. 100 90 80 7 0 110 100 1 80 10 60 120 70 120 50 0 60 13 13 0 50. 140 130 120 1 10 150 50 60 10 0 7 0 30 40 80 90. 80 100 70 110 80 90 10 0 11 6 0 2 0 0 1 0 7 1 20 5 0 60 3 1 13 0 0 50. 18 0 160 0 20 17 10. 0. B’. C’. HS 2. A=.... ;A’= .... . A......A’. A=.... ;A’= .... . A......A’. B =.......;B’=...... . B......B’. B =.......;B’=...... . B......B’. C=........;C’=...... . C......C’. C=........;C’=...... . C......C’.

<span class='text_page_counter'>(16)</span> §o vµ nhËn xÐt c¸c gãc A vµ gãc A’ , gãc B vµ gãc B’, gãc C vµ gãc C’. A’. A B Bài cho:. AB = A'B' ; AC = A'C' ; BC = B'C'. Kết quả đo: Le Thi Phu. B’. C. ˆ C ˆ Aˆ Aˆ ;Bˆ Bˆ ;C. .  ABC =. C’  A'B'C'.

<span class='text_page_counter'>(17)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c). 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm •VÏ ®o¹n th¼ng BC=4cm. •Trªn cïng mét nöa mÆt ph¼ng bê BC, A vÏ cung trßn t©m B, b¸n kÝnh 2cm. •VÏ cung trßn t©m C, b¸n kÝnh 3cm. •Hai cung trßn trªn c¾t nhau t¹i A. B C •VÏ ®o¹n th¼ng AB, AC, ta cã tam gi¸c ABC 2.Trêng hîp b»ng nhau c¹nh-c¹nh-c¹nh(c.c.c). Tính chất: SGK/113 Nếu ABC và A’B’C’ có: AB = A’B’. A.. A’.. AC=A’C’ thì Le Thi Phu. BC = B’C’ ABC = A’B’C’ (c.c.c). B. .. C B’. .. C’.

<span class='text_page_counter'>(18)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm •VÏ ®o¹n th¼ng BC=4cm. •Trªn cïng mét nöa mÆt ph¼ng bê BC, A vÏ cung trßn t©m B, b¸n kÝnh 2cm. •VÏ cung trßn t©m C, b¸n kÝnh 3cm. •Hai cung trßn trªn c¾t nhau t¹i A. B C •VÏ ®o¹n th¼ng AB, AC, ta cã tam gi¸c ABC 2.Trêng hîp b»ng nhau c¹nh-c¹nh-c¹nh(c.c.c). Tính chất: SGK/117 có: Nếu baNếu c¹nhABC củavà tamA’B’C’ giác này AB = A’B’. A.. A.. bằng ba c¹nh của tam giác kia thì hai tam AC=A’C’ giác đó bằng nhau. thì. Le Thi Phu. BC = B’C’ ABC = A’B’C’ (c.c.c). B. .. C B. .. C.

<span class='text_page_counter'>(19)</span> Qua bài học hôm nay chúng ta cần ghi nhớ điều gì? MNP và M'N'P' M'. M. Có MN = M'N' MP = M'P' NP = N'P' N. P. Le Thi Phu. N'. P'. thì MNP = ? M'N'P'.

<span class='text_page_counter'>(20)</span> TiÕt 23:Trêng hîp b»ng nhau thø nhÊt cña hai tam gi¸c c¹nh-c¹nh-c¹nh(c.c.c) 1. Vẽ tam giác biết ba cạnh Bµi to¸n:VÏ tam gi¸c ABC biÕt : BC = 4cm, AB = 2cm,AC = 3cm •VÏ ®o¹n th¼ng BC=4cm. •Trªn cïng mét nöa mÆt ph¼ng bê BC, A vÏ cung trßn t©m B, b¸n kÝnh 2cm. •VÏ cung trßn t©m C, b¸n kÝnh 3cm. •Hai cung trßn trªn c¾t nhau t¹i A. B C •VÏ ®o¹n th¼ng AB, AC, ta cã tam gi¸c ABC 2.Trêng hîp b»ng nhau c¹nh-c¹nh-c¹nh(c.c.c). Tính chất: SGK/117. Nếu ba c¹nh của tam giác này A. bằng ba c¹nh của tam giác kia thì hai tam giác đó bằng nhau. Le Thi Phu. B. A.. .. C B. .. C.

<span class='text_page_counter'>(21)</span> LUYỆN TẬP – CỦNG CỐ H·y t×m c¸c tam gi¸c b»ng nhau cã trong c¸c h×nh díi ®©y vµ gi¶i thÝch v× sao? A M. //. N. D. C //. /. B Hình 1. Le Thi Phu. P. Q. Hình 2.

<span class='text_page_counter'>(22)</span> LUYỆN TẬP – CỦNG CỐ Áp dụng. ?2/sgk Tìm sè ®o cña gãc B trªn. A 120. /. 0. //. D. C /. //. B Hình 67 Le Thi Phu. Hình 67.

<span class='text_page_counter'>(23)</span> LUYỆN TẬP – CỦNG CỐ. C¸c cÆp tam gi¸c ë h×nh 4 vµ h×nh 5 d¬Ý ®©y cã thÓ kÕt luËn b»ng nhau kh«ng? V× sao?. H×nh 4 H×nh 5. Le Thi Phu.

<span class='text_page_counter'>(24)</span> Trường hợp bằng nhau thứ nhất của tam giác cạnh-cạnh-cạnh(c.c.c). Tiết 23. Áp dụng M. N. P. Q. Hình 2. Chứng minh MN // PQ. Le Thi Phu. MN // PQ. NMP=MPQ. MNP = PQM.

<span class='text_page_counter'>(25)</span> Häc mµ vui-vui mµ häc. Le Thi Phu.

<span class='text_page_counter'>(26)</span> A. B. C. B’. A’. C’. Quan s¸t h×nh vÏ vµ cho biÕt cÇn thªm ®iÒu kiÖn g× th× tam gi¸c ABC b»ng tam gi¸c A’B’C’ theo trêng hîp c.c.c? Le Thi Phu.

<span class='text_page_counter'>(27)</span> Cám ơn bạn đã tham gia phÇn vui häc nµy!!!. Le Thi Phu.

<span class='text_page_counter'>(28)</span> Nếu. ABC và A’B’C’ có: A’B’ AB = ..... AC …..=A’C’ BC B’C’ .…..= …... thì. Le Thi Phu. ABC =. A’B’C’ (c.c.c).

<span class='text_page_counter'>(29)</span> H·y ph¸t biÓu trêng hîp b»ng nhau thø nhÊt(c.c.c) cña hai tam gi¸c?. Quµ cña b¹n lµ mét trµng ph¸o tay cña c¸c c¶ líp! Le Thi Phu.

<span class='text_page_counter'>(30)</span> B¹n lµ ngêi rÊt may m¾n đã nhận đợc quà! Le Thi Phu.

<span class='text_page_counter'>(31)</span> 1. Le Thi Phu. 2. 3. 4.

<span class='text_page_counter'>(32)</span> Bạn đã nhận đợc mét trµng ph¸o tay cña c¸c b¹n!. Le Thi Phu.

<span class='text_page_counter'>(33)</span> Hướng dẫn về nhà - Nắm vững cách vẽ tam giác biết ba cạnh +) Lưu ý:. Điều kiện để vẽ được tam giác khi biết ba cạnh là cạnh lớn nhất phải nhỏ hơn tổng hai cạnh còn lại. - Học thuộc và biết vận dụng trường hợp bằng nhau thứ nhất của tam giác vào giải bài tập - Bài tập : 16 , 18 , 20 , 21 , 22 (SGK). Le Thi Phu.

<span class='text_page_counter'>(34)</span> Tiết học đến đây là kết thóc - xin ch©n thµnh c¶m ¬n quý thÇy c« vµ c¸c em häc sinh!. Le Thi Phu.

<span class='text_page_counter'>(35)</span> Le Thi Phu.

<span class='text_page_counter'>(36)</span> Le Thi Phu.

<span class='text_page_counter'>(37)</span> Le Thi Kim Tu Phu Thap.

<span class='text_page_counter'>(38)</span> Le ThiTruong Phu Cau. Tien.

<span class='text_page_counter'>(39)</span> Le Thi Phu Cau Long. Bien.

<span class='text_page_counter'>(40)</span> Le Thi Phu. Cau My Thuan.

<span class='text_page_counter'>(41)</span> CÇu long biªn – Hµ Néi. Tại sao khi xây dựng các công trình các thanh sắt Hãy quan sátgắn cácthành thanhhình giằng cầugiác? và cho nhận xét thường được tam. Le Thi Phu.

<span class='text_page_counter'>(42)</span> Viet Tien Le Thi Phu.

<span class='text_page_counter'>(43)</span>