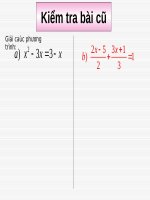phuong trinh chua an o mau tiet 47

<span class='text_page_counter'>(1)</span>TRƯỜNG THCS NGUYỄN DU. NhiÖt liÖt chµo mõng thÇy c« vÒ dù tiÕt to¸n LíP 8D.

<span class='text_page_counter'>(2)</span> Kiểm tra bài cũ Giải các phương trình sau?. b) 2.(x - 1) + 1 = x - 1. a) (x - 7).(5x + 2) = 0. Giải a) (x - 7).(5x + 2) = 0 b) 2.(x - 1) + 1 = x - 1 . x-7 = 0 hoặc 5x+2 = 0. * x-7 = 0  x=7 * 5x+ 2 = 0 . 2  x= 5. Vậy phương trình có tập nghiệm.  2  S  ;7   5 .  2x - 2 + 1- x + 1= 0  x=0 Vậy phương trình có tập nghiệm. S  0.

<span class='text_page_counter'>(3)</span> TIẾT TIẾT47 47. ë nh÷ng bµi tríc ta chØ xÐt c¸c ph¬ng tr×nh mµ hai vÕ cña nã lµ c¸c biÓu thøc h÷u tØ cña Èn vµ kh«ng chøa Èn ë mÉu . Trong bµi nµy ta sÏ nghiªn cøu c¸c ph¬ng tr×nh cã biÓu thøc chøa Èn ë mÉu..

<span class='text_page_counter'>(4)</span> TIẾT TIẾT47 47. (TiÕt 1). TiÕt 1: Tìm ĐKXĐ và giải phương trình TiÕt 2 : Áp dụng và giải phương trình Cách giải phương trình này như thế nào.

<span class='text_page_counter'>(5)</span> TIẾT TIẾT47 47 Kh«ng xác định. 1. Ví dụ mở đầu :. 1 1 Giải phương trình: x  1  x 1 x 1. Kh«ng x¸c định. Chuyển các biểu thức chứa ẩn sang một vế Ta biến đổi nh thế nào. 1 1 x  1 B»ng ph¬ng ph¸p x 1 x 1 quen thuéc. Thu gọn vế trái, ta được x = 1 Tr¶cña lêi * Qua x =1vÝkh«ng nghiÖm ơngđổi tr×nh v× t¹i x =mµ 1 dô nµylµcho ta thÊy khiph biÕn ph¬ng tr×nh 1đã Vậylµm khimÊt giải một phương trình chứa ẩn ở mẫu ta 1 1 Kh«ng VËy ph t ¬ng ¬ng tr×nh ® ¬ng v× cho kh«ng vµ ph cã ¬ng cïng tr×nh tËp nghiÖm. x=1 mÉu chøa Èn kh«ng cña ph¬ng tr×nh gi¸ trÞ ph©n thøc x¸c tr×nh định.thì phơng  0 x  1 phải tìm điều kiện xác định của phương trình. t¬ng đơng kh«ng? x ¬ng 1 tr×nh x trình 1 nhËn thÓ kh«ng đơng của víi ph ?1 Giá trị ®xîc= cã 1Cãcó phải làt¬ng nghiệm phương. không? V× sao?. ban ®Çu.

<span class='text_page_counter'>(6)</span> TIẾT TIẾT47 47 1. Ví dụ mở đầu : 2. Tìm điều kiện xác định của một phương trình : ®kx® cña ph¬ng tr×nh lµ ®iÒu kiÖn của ẩn để tất cả các mẫu trong phơng trình đều khác 0. Ví dụ 1 : Tìm điều kiện xác định của mỗi phương trình sau :. a). 2 x 1 1 x 2. b). 2 1 1  x 1 x2. Giải a) Ta thấy x – 2 ≠ 0 <=> x ≠ 2 Vậy ĐKXĐ : x ≠ 2 b) Ta thấy x – 1 ≠ 0 khi x ≠ 1 và x + 2 ≠ 0 khi x ≠ - 2 Vậy ĐKXĐ : x ≠ 1 và x ≠ -2 ®kx® cña ph¬ng tr×nh lµ g×?.

<span class='text_page_counter'>(7)</span> Bài tập hoạt động nhóm: Nối mỗi câu ở cột trái với một câu ở cột phải đề đợc kết qủa đúng. §KX§. Ph¬ng tr×nh. x 2 x  x 1 x 1 3 x 1  x b) x 2 x2 3 x 1 x c)   x 3 x2 x2 d) 1  5 x  4 2 x  2 x 1 a). 1) x ≠ 2 vµ x≠ -2 2) x ≠ 1 vµ x≠ -1 3) x ≠ 3 vµ x≠ -2 4) x ≠ 1 vµ x ≠ 2. 5) x ≠ - 1.

<span class='text_page_counter'>(8)</span> TIẾT TIẾT47 47 1. Ví dụ mở đầu : 2. Tìm điều kiện xác định của phương trình : ®kx® cña ph¬ng tr×nh lµ ®iÒu kiÖn của ẩn để tất cả các mẫu trong phơng trình đều khác 0 3. Giải phương trình chứa ẩn ở mẫu. ë bíc nµy ta dïng kÝ hiÖu suy ra (=>) không dùng kí hiệu tơng đơng (<=>). Ví dụ 2 : Giải phương trình x2 2x  3  (1) x 2( x  2) Phương pháp giải -ĐKXĐ : x ≠ 0 và x ≠ 2 MC: 2x(x - 2) - Quy đồng mẫu 2 vế của phương trình : 2( x  2)( x  2) x(2 x  3)  2 x( x  2) 2 x ( x  2) => 2(x + 2)(x – 2) = x(2x + 3) (1a) <=> 2(x2 - 4) = 2x2 + 3x <=> 2x2 - 8 = 2x2 + 3x <=> - 8 = 2x2 + 3x – 2x2 <=> 3x = - 8 8 <=> x =  ( thỏa mãn ĐKXĐ) 3. Vậy tập nghiệm của phương trình (1) là  8 S    3.

<span class='text_page_counter'>(9)</span> TIẾT TIẾT47 47 1. Ví dụ mở đầu : 2. Tìm điều kiện xác định của phương trình : ®kx® cña ph¬ng tr×nh lµ ®iÒu kiÖn của ẩn để tất cả các mẫu trong phơng trình đều khác 0 3. Giải phương trình chứa ẩn ở mẫu * Bước 1 : Tìm ĐKXĐ của phương trình. * Bước 2 : Quy đồng mẫu hai vế của phương trình rồi khử mẫu. * Bước 3 : Giải phương trình vừa nhận được. * Bước 4 : Kết luận, các giá trị thỏa mãn ĐKXĐ chính là nghiệm của phương trình đã cho. Ví dụ 2 : Giải phương trình x2 2x  3  (1) x nêu 2( xcác  2) bước Hãy Phương pháp để giảigiải một -ĐKXĐ : x ≠ 0 và x ≠ 2. phương trình MC: 2x(x chứa ẩn- 2)ở mẫu ?. - Quy đồng mẫu 2 vế của phương trình : 2( x  2)( x  2) x(2 x  3)  2 x( x  2) 2 x( x  2) => 2(x + 2)(x – 2) = x(2x + 3) (1a) <=> 2(x2 - 4) = 2x2 + 3x <=> 2x2 - 8 = 2x2 + 3x <=> - 8 = 2x2 + 3x – 2x2 <=> 3x = - 8 8 <=> x =  ( thỏa mãn ĐKXĐ) 3. Vậy tập nghiệm của phương trình (1) 8 là S = {  } 3.

<span class='text_page_counter'>(10)</span> TIẾT TIẾT47 47 1. Ví dụ mở đầu : 2. Tìm điều kiện xác định của phương trình : ®kx® cña ph¬ng tr×nh lµ ®iÒu kiÖn của ẩn để tất cả các mẫu trong phơng trình đều khác 0 3. Giải phương trình chứa ẩn ở mẫu * Bước 1 : Tìm ĐKXĐ của phương trình. * Bước 2 : Quy đồng mẫu hai vế của phương trình rồi khử mẫu. * Bước 3 : Giải phương trình vừa nhận được. * Bước 4 : Kết luận, các giá trị thỏa mãn ĐKXĐ chính là nghiệm của phương trình đã cho. Bài tập: Bµi 27 tr22 SGK Gi¶i ph¬ng tr×nh sau:. a). 2x  5 3 x 5. -§KX§ : x -MC: x + 5. Bµi gi¶i:.  5. 2x  5 3  2 x  5  3 x  5 x 5 x 5 x 5  2 x  5 3x  15  2 x  3 x 15  5.   x 20  x  20 ( thỏa mãn ĐKXĐ) VËy tËp nghiÖm cña ph¬ng tr×nh S = {-20}.

<span class='text_page_counter'>(11)</span> Sơ đồ các bước giải phương trình chứa ẩn ở mẫu. Home.

<span class='text_page_counter'>(12)</span> CỦNG CỐ Hãy tìm và chỉ ra những chỗ sai trong bài giải phương trình sau đây và sửa lại cho đúng:. x2  5x 5(1) x 5 Giải ĐKXĐ: x ≠ 5 x2 – 5x = 5(x – 5) (1a). . x2 – 5x = 5x – 25 x2 – 10x + 25 = 0 (x – 5)2 = 0 x = 5 (không thỏa mãn ĐKXĐ) Vậy tập nghiệm của phương trình là S = Ø.

<span class='text_page_counter'>(13)</span> TrườngưTHcs Nguyễn Du. Hướng dẫn về nhà: 1. Về nhà học kĩ lý thuyết 2. Nắm vững các bước giải phương trình. 3. Xem kĩ các bài tập giải trên lớp. 4. Bài tập về nhà : BT 27, 28 trang 22 ( SGK).

<span class='text_page_counter'>(14)</span> Xin caûm ơn quyù Thaày Coâ vaø caùc em hoïc sinh chuùc moät naêm mới sức khỏe và hạnh phúc..

<span class='text_page_counter'>(15)</span>