Tài liệu Biến Đổi Năng Lượng Điện Cơ - Phần 3 ppt

1Lecture 3
BÀI GIẢNG
Biến Đổi Năng Lượng Điện Cơ
TS. Hồ Phạm Huy Ánh
March 2010
/>2Lecture 3
¾ Cách vận hành của các hệ thống điện và cơ điện được giài thích dựa
trên lý thuyết trường điện từ.
¾ Dựa trên nền tảng chung là các hệ thống điện trường và từ trường,
ta vận dụng chủ yếu
hệ thống từ trường.
¾ Đầu tiên ta khảo sát các phương trình Maxwell
Giới Thiệu Chung
0
0
=•
=•
•
∂
∂
−=•
•=•
∫
∫
∫∫
∫∫
S
S
f
SC
S

f
C
danB
danJ
dan
t
B
ldE
danJldH
Ampere’s law
Faraday’s law
Luậtbảo toàn điện tích
Gauss’s law
3Lecture 3
¾ Là mạch từ không có phần tử cơ nào di động.
¾ Hình vẽ minh họa lõi từ có dạng vòng xuyến với N vòng dây. r
0
và r
1
lần
lượt là bán kính trong và ngoài của lõi từ.
Gọi
r là bán kính trung bình r = (r
0
+ r
1
) / 2, giả thiếtcường độ từ trường H
c
là
đồng nhất trong lõi thép. Dùng định luậtAmpere tacó: H

c
(2
π
r) = Ni. Hay,
Mạch từ tĩnh
NilH
cc
=
Trong đó l
c
= 2
π
r là chiềudàiđường sức trung bình
trong lõi. Giả sử mật độ từ B trong lõi thay đổituyến
tính theo H, ta có công thức:
()
2
/mWb
c
cc
l
Ni
HB
μμ
==
4Lecture 3
Ta xác định tiếp từ thông Φc
Với
μ
là giá trị từ thẩmcủavậtliệutừ, A

c
là tiếtdiệncắt ngang củalõi.
Ta định nghĩa Ni là sứctừđộng (magneto motive force-mmf), còn từ trễ
được định nghĩadựatrênđịnh luậtOhm Từ:
Wb
cc
c
c
ccc
Al
Ni
A
l
Ni
AB
μ
μ
φ
===
(At/Wb) R===
c
c
c
A
l
flux
mmfNi
μφ
P = 1/R gọilàtừ dẫn. Từ thông liên kết
λ

= N
φ
c
= PN
2
i. Cũng từđịnh
nghĩa, tự cảm L củacuộn dây đượcxác đi6nh bỡi:
R
P
2
2
N
N
i
L ===
λ
Mạch từ tĩnh (tt)
5Lecture 3
¾ Như vậy có sự tương đồng rất lớn giữa mạch điện và mạch từ
econductancpermeance
resistancereluctance
currentflux
voltagemmf
⇔
⇔
⇔
⇔
¾ Xét mạch từ có khe hở không khí (bỏ qua từ tản): Cần tìm chính xác
cường độ từ trường H trong lỏi thép cũng như H qua khe hở. Gọi l
g

–
độ rộng khe hở không khí, l
c
–chiều dài đường sức trung bình qua lõi.
Ta có kết quả:
c
r
c
g
g
ccgg
l
B
l
B
lHlHNi
00
μμμ
+=+=
Trong đó μ
0
= 4π x 10
−7
H/m là từ thẩm tuyệt đối của không khí, còn μ
r
là giá trị từ thẩm tương đối của vật liệu từ.
Mạch từ tĩnh (tt)
6Lecture 3
Áp dụng định luật Gauss’s cho mặtcắccựctừ lõi thép, B
g

A
g
= B
c
A
c.
Với, A
g
= A
c
. Nên, B
g
= B
c
. Chia sứctừđộng mmf cho từ thông ta xác
định đượctừ trỡ tương đương:
Trong đó R
g
và R
c
lần lượt là từ trỡ của khe hở không khí và của lỏi
thép. Chúng được thể hiện nối tiếp trong mạch từ tương đương.
cg
c
c
g
g
A
l
A

l
Ni
RR +=+=
μμφ
0
¾ Trường hợp khe hở bị toe cạnh “fringing”, i.e., lúc này từ tản xuất
hiện. Giả sử, A
g
> A
c
, i.e., phần diện tích khe hở hiệu dụng tăng lên.
Lúc này ta có thể dùng công thức kinh nghiệm,
(
)
(
)
gggc
lblaAabA +
+
=
=
,
Mạch từ tĩnh (tt)
7Lecture 3
Các Ví Dụ và Bài Tập:
¾ BT 3.1: Tìm sức từ động cần có để bảo đảm mật độ từ B mong
muốn. Đã biệt tiết diện khe hở và tiết diện mặt cắt lõi thép.
()( )( )
()()
()

()
Wb105.5101.15.0
At/Wb 1023.7
101.1104
001.0
At/Wb 107.47
1010410
06.0
44
6
47
g
3
474
−−
−−
−−
×=×==
×=
××
=
×=
×
=
gg
c
AB
φ
π
π

R
R
Cuối cùng ta được,
(
)
(
)
At 400105.51072307.47
53
=×××+=+=
−
φ
gc
Ni RR
8Lecture 3
¾ BT 3.2: Vác định từ thông qua cuộn dây. Các khe hở không khí có
cùng chiếu dài và tiết diện. Xem từ thẩm của thép bằng vô cùng cũng
như bỏ qua từ tản và từ rò.
Từ mạch tương đương ta xác định được
chiều của
φ
1
,
φ
2
, và
φ
3
. Từ giá trĩ từ thông
tổng của 3 từ thông tại nút a sẽ bằng zero.

Gọi
F là sức từ động từ a đến b, ta được:
(
)
()()
At/Wb 10989.1
104104
101.0
6
47
2
321
×=
××
×
====
−−
−
π
RRRR
2500
500
1500
R
R
R
φ
1
φ
2

φ
3
ba
0
15005002500
=
+
−
−
+
−
R
F
R
F
R
F
Cuối cùng ta được,
Wb10,0, Wb10,500
3
32
3
1
−−
−====
φφφ
F
Các Ví Dụ và Bài Tập (tt):
9Lecture 3
¾ Bài Tập 1: Một lõi từ dạng xuyến có bán kính mạch từ trung bình 500

mm, mật độ từ thông trong khe hở là 0.6 Wb/m
2
, quấn cuộn dây 100
vòng. Độ rộng khe hở là 2mm. Cho a = 20 mm. Bỏ qua từ trỡ lỏi thép
(=zero).
a) Xác định dòng kích từ qua cuộn dây
b) Xác định từ cảm L của cuộn dây
¾ Câu hỏi tự luận: SV được yêu cầu thiết kế cuộn cảm có tự cảm biến
thiên tuyến tính. Hãy trình bày hướng thiết kế của mình, có xét đến từ
rò và từ trỡ của lõi thép?
Các Ví Dụ và Bài Tập (tt):
10Lecture 3
Điện cảm tương hổ
¾ Điện cảm tương hổ là thông số liên quan đến điện áp cảm ứng trên 1
cuộn dây do dòng biến thiên qua 1 cuộn dây khác.
¾ Khảo sát 2 cuộn dây quấn trên cùng 1 mạch từ, cuộn 1 để kích thích
trong khi cuộn 2 để hở. Từ thông móc vòng qua cuộn 1 được tính bằng
21111
φ
φ
φ
+
=
l
Trong đó
φ
l1
(còn gọi là từ rò) chỉ móc vòng qua cuộn 1; trong khi,
φ
21

là
từ thông móc vòng tương hổ qua cả hai cuộn dây, nên sẽ hình thành từ
thông liên kết qua cuộn 2 nhờ tác động của dòng chảy qua cuộn 1.
¾ Vì cuộn 2 hở mạch nên từ thông móc vòng của cuộn này sẽ bằng
2122
φ
λ
N
=
11Lecture 3
¾
φ
21
tỉ lệ tuyến tính với dòng i
1
, nên
¾ Điện áp cảm ứng v
2
(do biến thiên của từ thông liên kết) xác định bởi:
M
21
được gọi là điện cảm tương hổ giữa 2 cuộn dây. Tương tự, Điện áp
cảm ứng v
1
trên cuộn 1 được xác định như sau.
φ
11
tỉ lệ với i
1
, nên , do đó

Với L
1
là giá trị tự cảm của cuộn 1, như ta đã biết.
1212122
iMN
=
=
φ
λ
dt
di
M
dt
d
v
1
21
2
2
==
λ
111111
iLN
=
=
φ
λ
dt
di
L

dt
d
v
1
1
1
1
==
λ
Điện cảm tương hổ (tt)
12Lecture 3
¾ Ta lại xét trường hợp cuộn 1 hở và cuộn 2 được kích thích. Ta lại
tiến hành các bước tương tự để xác định các điện áp cảm ứng.
Trong đó L
2
là giá trị tự cảm của cuộn 2, như ta đã biết.
222222
iLN
=
=
φ
λ
dt
di
L
dt
d
v
2
2

2
2
==
λ
2121211
iMN
=
=
φ
λ
dt
di
M
dt
d
v
2
12
1
1
==
λ
12222
φ
φ
φ
+=
l
¾ Theo qui tắc cân bằng năng lượng ta có: M
21

= M
12
= M.
¾ Cuối cùng ta xét trường hợp cả 2 cuộn dây cùng được kích thích.
1211122111
φ
φ
φ
φ
φ
φ
+
=
++=
l 2221122212
φ
φ
φ
φ
φ
φ
+
=
+
+
=
l
Điện cảm tương hổ (tt)
13Lecture 3
¾ Lưu ý rằng M

21
= M
12
= M
¾ Từ đóta cóhệ số ghép cặp giữa 2 cuộn dây :
¾ Dễ thấy rằng 0 ≤ k ≤ 1, hay tương ứng là,
¾ Các biến thế lỏi không khí thường có hệ số ghép cặp nhỏ (k < 0.5),
trong khi biến thế lỏi sắt từ thường có hệ số ghép cặp lớn(k > 0.5, và
có thể tiến đến 1).
2111211111
MiiLNN
+
=
+=
φ
φ
λ
2212222122
iLMiNN
+
=
+
=
φ
φ
λ
¾ Lấy phi phân 2 biểu thức trên ta xác định được các giá trị điện áp cảm
ứng
dt
di

M
dt
di
Lv
21
11
+=
dt
di
L
dt
di
Mv
2
2
1
2
+=
21
LL
M
k =
21
0 LLM ≤≤
Điện cảm tương hổ (tt)
14Lecture 3
Ví Dụ:
¾ BT 3.4: Mạch từ minh họa từ trỡ tương ứng với 3 khe hở không khí. Dùng
mạch từ tương đương xác định từ thông liên kết và tự cảm tương ứng.
Giải hệ 2 phương trình ta tìm được

φ
1
và
φ
2
N
1
i
1
R
1
R
2
R
3
N
2
i
2
φ
1
φ
2
()
1121311
φ
φ
φ
RR
+

−=iN
(
)
2132222
φ
φ
φ
−
−
=
RRiN
()
6
211
1025100 ×−=
φφ
i
(
)
6
212
1042100 ×+−=
φφ
i
()
6
211
105.1225
−
×+= ii

φ
(
)
6
212
1025.315.12
−
×+= ii
φ
Đồng thời
mH 5.2H 1025
4
1
=×=
−
L
mH 125.3H 1025.31
4
2
=×=
−
L
mH 25.1H 105.12
4
=×=
−
M
(
)
4

21111
105.1225
−
×+== iiN
φλ
(
)
4
21222
1025.315.12
−
×+== iiN
φλ
Nên ta tìm được
15Lecture 3
Chấm đánh dấu chiều quấn cuộn dây
¾ Luật Lenz qui định: áp cảm ứng sẽ có chiều sao cho dòng tạo ra sinh
từ thông ngược với chiều từ thông tạo ra áp cảm ứng đó.
¾ Chiều áp hình thành qua 2 đầu các cuộn dây tác động tương hổ được
xác định nhờ
Chấm đánh dấu chiều quấn cuộn dây. Qui tắc chung như
sau: Dòng i chảy vào đầu có đánh dấu (
đầu không đánh dấu ) của 1 cuộn
sẽ cảm ứng áp Mdi/dt với cực tính dương ở đầu có đánh dấu
(đầu không
đánh dấu)của cuộn tương hổ.
¾ Hai vấn đề đặt ra là: (1) với cuộn dây có sẳn hãy xác định chấm đánh
dấu chiều quấn. (2) với cuộn dây có sẳn chấm đánh dấu, hãy thiết lập hệ
phương trình cho mạch điện tương ứng.
16Lecture 3

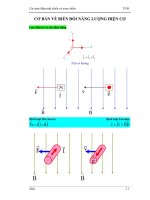
Cách xác định chấm đánh dấu chiều quấn cuộn dây
¾ Các bước cụ thể:
 Chọnngẩu nhiên 1 đầucuộn dây sơđểđánh dấuchấm.
 Giả sử dòng chảyvàođầucuộn dây có đánh dấuchấm, xác định
chiềutừ thông hình thành trong lõi.
 Chọnngẩu nhiên 1 đầucuộn dây thứđểcho dòng thử chảy vào.
 Xác định chiềutừ thông do dòng thử tạora.
 Nếu hai từ thông cùng chiều, đánh dấuchấmvàođầucuộn dây
thứ có dòng thử chả
y vào.
 Nếu hai từ thông ngượcchiều, đánh dấuchấmvàođầucuộn dây
thứ có dòng thử chảyra.
17Lecture 3
Phương pháp thực nghiệm xác định dấu chấm đánh dấu
¾ Để xác định chiếu quấn của 2 cuộn dây sơ và thứ của biến thế, ta áp
dụng phương pháp thực nghiệm sau:
Dùng nguốn DC kích thích cuộn
sơ của biến thế.
Đặt dấu chấm vào đầu cuộn sơ nối
vào nguồn + của nguồn DC.
Đóng khóa K: ghi nhận nếu kim volt kế quay thuận => đặt dấu chấm vào
đầu cuộn thứ nối vào nguồn + của volt kế. Ngược l
ại nếu kim volt kế quay
ngược => đặt dấu chấm vào đầu cuộn thứ nối vào nguồn - của volt kế.
+
_
18Lecture 3
Lập phương trình vòng kín cho mạch điện có cuộn dây tương hổ
¾ Cho 2 cuộn dây ghép cặp tương hổ. Hãy lập phương trình vòng kín.
Đầu tiên cho chọn chiều cho dòng bên sơ và thứ cấp.

QUI TẮC: Dòng chọn chảy vào đầu có chấm (không chấm) của cuộn dây,
sẽ cảm ứng điện áp dương ở đầu có chấm (không chấm) của cuộn
dây tương hổ. Tương tự Dòng chọn chảy vào đầu có chấm (không
chấm) của cuộn dây, sẽ cảm ứng điện áp âm ở đầu có chấm (không
chấm) của cuộn dây tương hổ.
v
1
v
2
R
1
R
2
i
1
i
2
M
dt
di
M
dt
di
LRiv
21
1111
++=
dt
di
M

dt
di
LRiv
12
2222
++=
19Lecture 3
¾ BT 3.6: Lập phương trình vòng kín cho mạch điện có cuộn dây tương hổ.
Giả thiết điện áp ban đầu qua tụ bằng zero.
i
1
R
2
C
L
1
R
1
i
2
v
1
M
L
2
(i
1
–i
2
)

() ()
()
212
2
12121
2
2
0
2
1
0
Rii
d
t
di
M
ii
dt
d
Lii
dt
d
M
dt
di
Ldti
C
t
−++
−+−−+=

∫
()
()
dt
di
Mii
dt
d
L
RiiRiv
2
211
221111
−−+
−+=
Bài Tập trong lớp
20Lecture 3
Bài Tập trong lớp
¾ BT 3.15.