Tài liệu Biến Đổi Năng Lượng Điện Cơ - Phần 1 docx

1Lecture 5
BÀI GIẢNG
Biến Đổi Năng Lượng Điện Cơ
TS. Hồ Phạm Huy Ánh
TS. Nguyễn Quang Nam
March 2010
/>2Lecture 5
¾ Ta tiếp tục khảo sát các mạch từ có chứa bộ phận di động.
¾ Có nhiều kết quả quan trọng được rút ra từ mô hình toán của các hệ
thống điện cơ thông số tập trung.
¾ Dòng cấp cho một hay nhiều cuộn dây quấn trên mạch từ sẽ tương
tác tạo lực hay mô men tác động trong hệ thống điện cơ.
¾ Nói chung, cả dòng kích cuộn dây lẫn lực từ đều là thông s
ố biến đổi
theo thời gian.
¾ Ta có thể lập được hệ phương trình vi phân cho các hệ điện cơ, và
đưa chúng về dạng không gian trạng thái, rất tiện dùng để mô phỏng,
nhận dạng, điều khiển, phân tích cũng như thiết kế.
Hệ Thống Điện Cơ –Giới Thiệu Chung
3Lecture 5
S
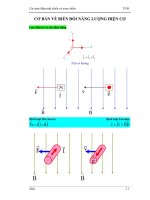
¾ Khảo sát hệ thống trên Hình. 4.1
¾ Áp dụng định luật Ampere
Ta được
¾ Luật Faraday
Các Hệ Thống Chuyển Dịch –
Ứng dụng của các luật điện từ
∫∫
⋅•=•
S
f

C
daJdlH
η
NiHl
=
∫∫
⋅•−=•
CS
daB
dt
d
dlE
η
()
dt
d
N
dt
d
v
λ
=Φ=
Cho ta
¾ Luật Gauss được áp dụng phụ thuộc vào thông số hình học và rất cần
khi hệ thống có sai khác về H
. Luật bảo toàn điện tích dẫn đến hệ quả
KCL.
Contour C
4Lecture 5
¾ Với các hệ thống chuyển dịch, λ = λ(i, x).

¾ Với các kết cấu đơn giản, có thể áp dụng luật Faraday
Cấu trúc của một hệ thống điện cơ
Hệ thống điện
(tập trung)
Ghép cặp
Điện-Cơ
Hệ thống cơ
(tập trung)
v, i, λ
f
e
, x or T
e
, θ
dt
dx
xdt
di
idt
d
v
∂
∂
+
∂
∂
==
λ
λ
λ

transformer voltage speed voltage
5Lecture 5
Do đó,
Hệ thống điện tuyến tính
(
)
ixL
=
λ
()
(
)
dt
dx
dx
xdL
i
dt
di
xLv +=
¾ Ta đã có với hệ tĩnh
Li
=
λ
dt
di
Lv =
and
¾ Trường hợp hệ nhiều cửa
∑∑

==
∂
∂
+
∂
∂
==
M
j
j
j
k
N
j
j
j
kk
k
dt
dx
xdt
di
idt
d
v
11
λλλ
Nk , ,2,1
=
¾ Lúc này lực và từ thông liên kết có thể là hàm phụ thuộc nhiều biến.

Vì:
6Lecture 5
Tìm H
1
, H
2
, λ, và v, với các giả định sau: 1) μ = ∞ với mạch từ, 2) g >>
w, x >> 2w và 3) bỏ qua từ rò.
Ví Dụ 4.1
(
)
(
)
(
)
022
2010
=
−
wdHwdH
μ
μ
xg
Ni
HH
+
==
21
Đưa đến
Luật Gauss cho

xg
iNwd
N
+
=Φ=
2
0
2
μ
λ
Từ thông liên kếtlà
Suy ra tự cảm
()
xg
Nwd
xL
+
=
2
0
2
μ
()
()
dt
dx
xg
iNwd
dt
di

xg
Nwd
tv
2
2
0
2
0
22
+
−
+
=
μμ
Điệnáp
7Lecture 5
¾ VD 4.2: Dùng Hình 4.7. Tìm λ
s
, λ
r
là hàm theo i
s
, i
r
, và θ. Tìm v
s
và v
r
có trên dây quấn rô to. Giả thiết μ = ∞, và g << R và l.
Các hệ thống quay

31 r
rrss
r
H
g
iNiN
H −=
−
=
42 r
rrss
r
H
g
iNiN
H −=
+
=
(
)
lRHNlRHNN
rsrssss
θ
π
μ
θ
μ
φ
λ
−

+
=
=
2010
Đơngiản đitacòn
rrssss
iLNNiLN
⎟
⎠
⎞
⎜
⎝
⎛
−+=
π
θ
λ
2
1
00
2
Tiến hành tương tự ta được,
rrsrsr
iLNiLNN
0
2
0
2
1 +
⎟

⎠
⎞
⎜
⎝
⎛
−=
π
θ
λ
π
θ
<
<
0
π
θ
<
<
0
() () ()
dt
d
Mi
dt
di
M
dt
di
Ltv
r

r
s
ss
θ
θθ
sincos −+=
Vớicácmáyđiệnthựctế, ta có
8Lecture 5
¾ Xác định λ
1
và λ
2
rồi suy ra tự cảm cùng hổ cảm của hệ thống cho
trên hệ điện cơ Hình 4.14, sử dụng mạch từ tương đương như hình vẽ.
Ví Dụ 4.4
R
x
R
x
R
x
N
2
i
2
N
1
i
1
Φ

1
Φ
2
2
0
0
W
x
A
x
R
x
μ
μ
==
2111
2
Φ
+
Φ=
xx
RRiN
2122
2
Φ
+
Φ=
xx
RRiN
()

2211
2
1
2
0
111
2
3
iNNiN
x
W
N −=Φ=
μ
λ
()
2
2
2121
2
0
222
2
3
iNiNN
x
W
N +−=Φ=
μ
λ
¾ Câu hỏi tự luận: Liệu ta có thể đồng nhất tự cảm và hổ cảm hay không ?

9Lecture 5
¾ Lực điện phát sinh có các dạng f
e
= f
e
(i, x) = f
e
(λ, x) (vì i có thể được
tính từ λ = λ(i, x)) được khảo sát với hệ thống 1 cổng điện 1 cổng cơ.
¾ Lưu ý f
e
luôn luôn tác động theo chiều x dương.
¾ Cụ thể ta khảo sát hệ thống trên Hình 4.17, được đưa về dạng biểu
đồ thể hiện trên Hình 4.18. Gọi W
m
là năng lượng hệ thống, theo nguyên
lý bảo toàn năng lượng
Lực phát sinh dựa trên thành phần năng lượng
Mứcbiến đổi
Năng lượng
Công suất điện
đầuvào
Công suấtcơ
đầura
=
_
dt
dx
f
dt

d
i
dt
dx
fvi
dt
dW
ee
m
−=−=
λ
dxfiddW
e
m
−=
λ
or
¾ Các biến (một cơ, một điện) có thể được chọn độc lập, mà không vi phạm bản
chất vật lỳ của hệ đang được khảo sát. Giả sử (λ, x) là cặp biến được chọn.
10Lecture 5
¾ Vì hệ thống được bảo toàn, mức năng lượng biến động khi phần tử động của
hệ di chuyển từ a đến b trong mặt phẳng λ –x sẽ không phụ thuộc đường lấy
tích phân a-b (xem Hình 4.19). Khi đường A được chọn
()() () ()
∫∫
+−=−
b
a
b
a

dxidxxfxWxW
b
x
x
a
e
aambbm
λ
λ
λλλλλ
,,,,
¾ Khi đường B được chọn, ta được
()()() ()
∫∫
−=−
b
a
b
a
x
x
b
e
aaambbm
dxxfdxixWxW ,,,,
λλλλλ
λ
λ
¾ Cả 2 phương án A và B đều phải cho kết quả giống nhau. Ta để ý nếu λ
a

= 0,
sẽ không có lực phát sinh, vì thế phương án A sẽ dễ tính hơn, cho ta kết quả:
()() ()
∫
=−
b
dxixWxW
bambbm
λ
λλλ
0
,,0,
¾ Tổng quát hóa theo phương pháp này, ta có công thức tính
() ()
∫
=
λ
λλλ
0
,, dxixW
m
Lực phát sinh dựa trên thành phần năng lượng (tt)
11Lecture 5
¾ Ta cần nhớ lại:
Quan hệ giữa lực phát sinh và năng lượng
dxfiddW
e
m
−=
λ

¾ Vì W
m
= W
m
(λ, x), vi phân của W
m
được phân tích thành
(
)
(
)
dx
x
xW
d
xW
dt
dW
mmm
∂
∂
+
∂
∂
=
,,
λ
λ
λ
λ

¾ Cân bằng hai phương trình trên sẽ cho ta
(
)
λ
λ
∂
∂
=
xW
i
m
,
(
)
x
xW
f
m
e
∂
∂
−=
,
λ
12Lecture 5
¾ Hãy xác định các lực f
e
(λ, x) và f
e
(i, x) của hệ thống cho ở Hình 4.1

Bài tập 4.5
gx
i
L
gx
i
g
Nwd
xg
iNwd
N
+
=
+
=
+
=Φ=
11
22
0
2
0
2
0
μμ
λ
()
gx
L
i += 1

0
λ
() () ()
gx
L
dgx
L
dxiW
m
+=+==
∫∫
1
2
1,
0
2
0
0
0
λ
λ
λ
λλ
λλ
()
gL
x
x
W
f

m
e
0
2
2
,
λ
λ
−=
∂
∂
−=
()
() ()
2
2
0
2
0
22
0
1
2
1
12
,
gx
iL
gxgL
iL

xif
e
+
−=
+
−=
Giải ra theo i ta được
Từđótaxácđịnh f
e
13Lecture 5
¾
Bài Tập giải ở Lớp