Ôn tập chương 4 đại số 10

TOÁN

THPT

ĐẠI SỐ 10

LỚP

10
ĐẠI SỐ 10

Chương IV: BẤT ĐẲNG THỨC – BẤT PHƯƠNG TRÌNH

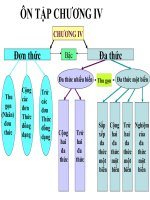
ƠN TẬP CHƯƠNG IV
I

HỆ THỐNG KIẾN THỨC

II

ÁP DỤNG

III

BÀI TẬP TRẮC NGHIỆM

IV

BÀI TẬP VỀ NHÀ

TỐN

I.

THPT

ĐẠI SỐ 10

HỆ THỐNG KIẾN THỨC
BẤT ĐẲNG THỨC

- Tính chất của bất đẳng thức
- Bất đẳng thức Cauchy và hệ quả
- Bất đẳng thức chứa dấu giá trị tuyệt đối

BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT
PHƯƠNG TRÌNH MỘT ẨN

- Điều kiện của bất phương trình, hệ bất
phương trình
- Một số phép biến đổi bất phương trình

DẤU CỦA NHỊ THỨC
BẬC NHẤT

- Định lý về dấu của nhị thức bậc nhất

BẤT PHƯƠNG TRÌNH
BẬC NHẤT 2 ẨN

DẤU CỦA TAM THỨC BẬC HAI

- Biểu diễn tập nghiệm của BPT bậc nhất 2 ẩn

- Định lý về dấu của tam thức bậc hai


TOÁN

THPT

ĐẠI SỐ 10

II. ÁP DỤNG

Bài 1

Chứng minh rằng

Bài giải
Áp dụng BĐT Cauchy cho 2 số dương a, b ta có:

Đẳng thức xảy ra


TỐN

THPT

Bài 2

ĐẠI SỐ 10

Giải các bất phương trình sau

Bài giải
Điều kiện:

Kết hợp điều kiện, BPT có tập
nghiệm

Điều kiện:

Kết hợp điều kiện, BPT có tập
nghiệm


TỐN

THPT

Bài 3

ĐẠI SỐ 10

Giải bất phương trình sau

Bài giải
Bảng xét dấu

Bảng xét dấu
|

Vế
Vế
trái
trái
Vậy

|

|

|
Vế trái
Vậy


TOÁN

THPT

ĐẠI SỐ 10

Bài 4
Biểu diển miền nghiệm của bất phương trình

Bài giải

Vẽ đường thẳng

Lấy điểm
Ta thấy nên nửa mặt phẳng bờ không chứa gốc
tọa độ O (phần màu xanh) là miền nghiệm của
của bất phương trình (khơng kể những điểm trên )


TỐN

Bài 5

THPT

ĐẠI SỐ 10

Giải bất phương trình sau

Nhắc lại


TỐN

Bài 5

THPT

ĐẠI SỐ 10

Giải bất phương trình sau

Bài giải

Vậy tập nghiệm

Vậy tập nghiệm


TỐN

THPT

ĐẠI SỐ 10

Bài 6

Tìm tất cả giá trị của m để hàm số
Bài giải


TOÁN

THPT

ĐẠI SỐ 10

III. CÂU HỎI TRẮC NGHIỆM
CÂU 1
15

A
A

54 của bất phương trình
9
Tập nghiệm

.

B

C

Bài giải

.
Chọn

D
Bảng xét dấu:

Ta có: .
Và: .
Vậy tập nghiệm của bất phương
trình đã cho là

6

|
Vế
Vế
trái

trái

|


TỐN

CÂU 2
15

A

THPT

ĐẠI SỐ 10

Tập nghiệm54
của bất phương trình
9 là

B

D
D

C

Bài giải

(2;4]

Bảng xét dấu:

Điều kiện .
Xét .
Và .
Vậy tập nghiệm của bất phương
trình đã cho là .
Chọn D.

6

Vế
trái
Vế trái

|
0
||

0
|
0


TỐN

CÂU 3
15

THPT

54của bất phương trình
9 .
Tập nghiệm

B

A

ĐẠI SỐ 10

Bài giải
Ta có . Chọn C

C
C

6

D


TỐN

CÂU 4
15

A

THPT

ĐẠI SỐ 10

54của bất phương trình
9
Tập nghiệm

B

C

Bài giải
Ta có .
Xét tam thức có hai nghiệm , , hệ số , nên luôn dương với mọi thuộc khoảng .
Vậy bất phương trình có tập nghiệm là khoảng . Chọn D

6

D
D


TỐN

CÂU 5
15

THPT

54 của bất phương 9
Tập nghiệm
trình
B
B

A

ĐẠI SỐ 10

C

Bài giải
Ta có .
Vậy tập nghiệm của bất phương trình là .
Chọn B.

6

D


TỐN

CÂU 6
15

A
A

THPT

ĐẠI SỐ 10

54
9
Tập nghiệm của bất phương trình
B

C

Bài giải
Ta có .
Vậy tập nghiệm của bất phương trình là .
Chọn A.

6

D


TỐN

CÂU 7
15

A
A

THPT

ĐẠI SỐ 10

54 của bất phương 9
Tập nghiệm
trình

B

.

C

Bài giải
Ta có .
Vậy bất phương trình vơ nghiệm.
Chọn A.

6

D


TOÁN

THPT

ĐẠI SỐ 10

CÂU 8

giá trị của tham số 9
để bất phương trình
15 Tìm tất cả các 54
6
vơ nghiệm

A
A

B

C

Bài giải
Bất phương trình vơ nghiệm khi và chỉ khi , .
Ta có .
Chọn A.

D


TỐN

THPT

ĐẠI SỐ 10

CÂU 9
Tìm
các

giá
trị
thực
của
tham
số
để
phương
trình
15
54
9
có hai nghiệm , thỏa

B
B

A

C

Bài giải
Với ta xét phương trình: .
Ta có .
Phương trình có hai nghiệm phân biệt khi và chỉ khi .
Ta có: .
Theo Vi-et ta có: , thay vào ta có: .

D

6


TỐN

THPT

ĐẠI SỐ 10

CÂU
15
54
9
10
ất phương trình có bao nhiêu nghiệm ngun trong ?

B
B

A

C

Bài giải
.
Mà
Vậy có giá trị nguyên thỏa mãn đề bài.
Chọn B.

6

D


TOÁN

THPT

ĐẠI SỐ 10

CÂU
Giá trị nhỏ nhất của biểu thức trên miền xác định bởi hệ là
15
54
9
11

A

B

C

Bài giải
Miền nghiệm của hệ là miền trong của tam giác kể cả biên (như
hình)
Ta thấy đạt giá trị nhỏ nhất chỉ có thể tại các điểm , , .
Tại thì .Tại thì . Tại thì .
Vậy khi , . Chọn D.

6

D
D


TỐN

THPT

ĐẠI SỐ 10

CÂU
15
54
9
6
12
Cho là số thực bất kì, . Bất đẳng thức nào sau đây đúng với mọi .

A

B
Bài giải
Với là số thực bất kì, ta có:
.
Hay .
Chọn D.

C

D
D


TOÁN

THPT

ĐẠI SỐ 10

CÂU
15
54
9
13
Cho nhị thức bậc nhất . Trong các mệnh đề sau, mệnh đề nào đúng?

A
B
B

Nhị thức có giá trị cùng dấu với hệ số khi lấy các giá trị trong khoảng .
Nhị thức có giá trị cùng dấu với hệ số khi lấy các giá trị trong khoảng .

C Nhị thức có giá trị trái dấu với hệ số khi lấy các giá trị trong khoảng .
D Nhị thức có giá trị cùng dấu với hệ số khi lấy các giá trị trong khoảng .
Bài giải

6

TỐN

THPT

ĐẠI SỐ 10

CÂU
Cho
các
số
dương
,
,
thỏa
mãn
.
15
54
14
Khi đó giá trị nhỏ nhất của biểu thức là

A

.

B
B

.

Bài giải
Áp dụng BĐT Cơ-si, ta có: .
Tương tự, ta có: , .
Suy ra: .
Dấu đẳng thức xảy ra .
Vậy . Chọn B.

9

C

6

D


TỐN

THPT

CÂU
15
15

A

ĐẠI SỐ 10

Cho hàm số9.
Tìm tất cả các giá trị của tham số để , .

54

B

Bài giải
Ta có , , .
, .
Vì nên , .
. (do đồng biến trên )
Chọn D.

C

D
D

6


TOÁN

THPT

ĐẠI SỐ 10

IV. BÀI TẬP VỀ NHÀ
Bài 1

Xác định để phương trình có ba nghiệm phân biệt lớn hơn .

Bài 2
Một xưởng cơ khí có hai cơng nhân là Chiến và Bình. Xưởng sản xuất loại sản
phẩm và . Mỗi sản phẩm bán lãi nghìn đồng, mỗi sản phẩm bán lãi nghìn đồng. Để
sản xuất được một sản phẩm thì Chiến phải làm việc trong giờ, Bình phải làm việc
trong giờ. Để sản xuất được một sản phẩm thì Chiến phải làm việc trong giờ, Bình
phải làm việc trong giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết
rằng trong một tháng Chiến không thể làm việc q giờ và Bình khơng thể làm việc
q giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là.