Giá trị tương lai của một dòng tiền đơn

GIÁ TRỊ TƯƠNG LAI CỦA MỘT DÒNG TIỀN ĐƠN
Trong phần này, chúng tôi giới thiệu giá trị thời gian kết hợp với dòng tiền đơn hay đầu
tư một lần. Chúng tôi diễn tả mối quan hệ giữa đầu tư ban đầu hay giá trị hiện tại (PV),
là giá trị mà thu được một tỷ suất lợi tức (lãi suất cho mỗi giai đoạn) biểu thị là r, và giá
trị tương lai của nó (FV), là giá trị mà sẽ nhận được sau N năm hoặc khoảng thời gian kể
từ ngày hơm nay.
Ví dụ sau đây sẽ làm rõ khái niệm này. Giả sử bạn đầu tư $100 (PV = $100) vào một tài
khoản ngân hàng mà trả lãi 5% hàng năm. Vào cuối năm thứ nhất, bạn sẽ có $100 cộng
với lãi thu được, 0.05 × $100 = $5, tổng cộng là $105. Để chính thức hóa ví dụ một giai
đoạn này, chúng ta định nghĩa các thuật ngữ sau:
PV = giá trị hiện tại của khoản đầu tư
FVN = giá trị tương lai của khoản đầu tư sau N khoảng thời gian kể từ ngày hôm nay
R = lãi suất cho mỗi giai đoạn
Đối với N = 1, biểu hiện cho giá trị tương lai của một lượng PV là:
FV1 = PV (1+r)
FV1 = PV (1+r)
Đối với ví dụ này, chúng ta tính được giá trị tương lai sau một năm kể từ hôm nay là FV1
= $100(1.05) = $105.
Bây giờ giả sử bạn quyết định đầu tư số tiền ban đầu $100 trong hai năm với lãi suất thu
được sẽ ghi có vào tài khoản của bạn hàng năm (lãi kép hàng năm). Vào cuối năm thứ
nhất (đầu năm thứ hai), tài khoản của bạn sẽ có $105, số tiền này bạn sẽ để lại trong ngân
hàng thêm một năm nữa. Như vậy, với một số tiền ban đầu 105$ (PV = $105), số tiền vào
cuối năm thứ hai sẽ là $105(1.05) = $110.25. Lưu ý rằng 5.25$ tiền lãi thu được trong
năm thứ hai là 5% của số tiền đầu tư vào đầu năm 2.
Một cách khác để hiểu ví dụ này là để ý rằng số tiền đầu tư vào đầu năm 2 bao gồm số
tiền gốc ban đầu $100 mà bạn đầu tư cộng với $5 tiền lãi kiếm được trong năm đầu tiên.


Trong năm thứ hai, một lần nữa số tiền gốc ban đầu lại thu được lãi, cũng như lãi mà nó
thu được trong năm 1. Bạn có thể thấy số tiền đầu tư gốc ban đầu tăng lên như thế nào:
Đầu tư gốc ban đầu

$100.00

Lãi của năm thứ thứ nhất ($100 × 0.05)

5.00

Lãi của năm thứ hai dựa trên số tiền đầu tư gốc ban đầu ($100 × 0.05)

5.00

Lãi của năm thứ hai dựa trên số tiền lãi thu được của năm thứ nhất (0.05 ×$5.00 lãi trên
lãi)
Tổng cộng

0.25
$110.25

$5 tiền lãi mà bạn kiếm được ở mỗi giai đoạn dựa trên đầu tư gốc ban đầu $100 được gọi
là lãi đơn (tỷ lệ lãi suất nhân với vốn ban đầu). Vốn ban đầu là lượng tiền ban đầu đem
đầu tư. Trong khoảng thời gian hai năm, bạn kiếm được $10 lãi đơn. Phần được trả thêm
$0.25 mà bạn có vào cuối năm 2 là lãi mà bạn thu được từ lãi của năm 1 $5 mà bạn đem
tái đầu tư.
Lãi kiếm được dựa trên lãi cung cấp một cái nhìn sơ lược đầu tiên của hiện tượng được
gọi là lãi kép. Mặc dù lãi thu được dựa trên số tiền đầu tư ban đầu là quan trọng đối với
một tỷ lệ lãi suất nhất định tức là nó cố định ở một tỷ lệ từ giai đoạn này qua giai đoạn
khác. Lãi kép kiếm được trên tiền lãi tái đầu tư có ý nghĩa to lớn hơn rất nhiều bởi vì so
với một lãi suất nhất định, nó chỉ tăng ở một tỷ lệ nhất định trong mỗi giai đoạn. Giá trị
của lãi kép gia tăng độ lớn của lãi suất. Ví dụ $100 đầu tư ngày hơm nay sẽ trị giá khoảng
$13,150 sau 100 năm nếu lãi kép hàng năm ở mức 5%, nhưng sẽ trị giá hơn $20 triệu nếu

lãi kép hàng năm trong cùng khoảng thời gian trên ở tỷ lệ 13%.
Để xác minh con số 20 triệu, chúng ta cần một công thức chung để xử lý lãi kép cho bất
kỳ số lượng khoảng thời gian nào. Công thức tổng quát sau đây liên kết giá trị hiện tại
của một khoản đầu tư ban đầu với giá trị tương lai của nó sau một thời gian N:
FVN = PV(1+r)N


Trong đó r là lãi suất cơng bố của mỗi kỳ và N là số kỳ lãi kép. Trong ví dụ ngân hàng,
FV2 = $100(1 + 0.05)2 = 110.25 $. Trong ví dụ đầu tư 13%, FV100 = $100(1.13)100 =
$20,316,287.42.
Điểm quan trọng nhất cần nhớ về việc sử dụng phương trình giá trị tương lai là lãi suất
cơng bố r, và số kỳ lãi kép, N, phải tương thích. Cả hai biến này phải được xác định trong
cùng một đơn vị thời gian. Ví dụ, nếu N được định là hàng tháng, thì r nên là mức lãi suất
của một tháng, unannualized.
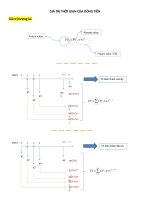
Một dòng thời gian giúp chúng ta theo dõi sự phù hợp về đơn vị thời gian và tỷ lệ lãi suất
mỗi thời kì. Trong dịng thời gian, chúng tôi sử dụng chỉ số thời gian t để đại diện cho
một thời điểm ở những khoảng thời gian đã định từ ngày hơm nay. Vì vậy, giá trị hiện tại
là số tiền dành cho đầu tư ngày hôm nay, được kí hiệu là t = 0. Bây giờ chúng ta có thể
suy ra thời điềm N thời kì kể từ ngày hơm nay là t = N. Dịng thời gian trong hình 1 cho
thấy mối quan hệ này.
Hình 1: Mối quan hệ giữa đầu tư ban đầu, PV, và giá trị tương lai của nó, FV

Trong hình 1, chúng ta có vị trí đầu tư ban đầu, PV, tại t = 0. Sử dụng phương trình 2,
chúng ta chuyển các giá trị hiện tại, PV, đến thời điểm t = N bằng cách nhân vào hệ số (1
+ r)N. Hệ số này được gọi là hệ số giá trị tương lai. Chúng ta biểu thị giá trị tương lai trên
dịng thời gian là FV, và vị trí của nó tại t = N. Giả sử giá trị tương lai thì được nhận
chính xác sau 10 kỳ kể từ ngày hôm nay (N = 10). Giá trị hiện tại, PV, và giá trị trong
tương lai, FV, được tách ra trong thời gian thông qua hệ số (1 + r)10.

Tóm lại giá trị hiện tại và giá trị trong tương lai được tách ra trong thời gian có những hệ
quả quan trọng:
 Chúng ta có thể cộng số tiền chỉ khi chúng được biểu thị tại cùng một thời điểm.
 Đối với một mức lãi suất cho trước (nhất định), giá trị tương lai tăng lên cùng với
số lượng thời kỳ.
 Đối với một số lượng thời kỳ cho trước (nhất định), giá trị tương lai tăng lên cùng
với lãi suất.
Để hiểu rõ hơn các khái niệm này, hãy xem xét ba ví dụ minh họa làm thế nào để áp
dụng cơng thức giá trị trong tương lai.
VÍ DỤ 1
Giá trị tương lai của một khoản tiền trả một lần bằng tiền mặt tạm thời tái đầu tư ở
mức tương tự.
Bạn là người may mắn trúng số được 5 triệu $ sau khi đã nộp thuế. Bạn đầu tư số tiền
này vào một chứng chỉ tiền gửi năm năm (CD) tại một định chế tài chính địa phương.
CD này hứa hẹn sẽ trả lãi 7% mỗi năm với lãi kép hàng năm. Định chế này cũng để
cho bạn tái đầu tư lãi ở tỷ lệ đó trong suốt thời gian tồn tại của CD. Bạn sẽ có bao
nhiêu tiền sau 5 năm nếu tiền của bạn vẫn được giữ lại để đầu tư ở mức lãi suất
7%/năm trong 5 năm mà khơng có rút tiền?
Giải pháp: để giải quyết vấn đề này, tính tốn giá trị tương lai của số tiền đầu tư 5
triệu $, sử dụng các giá trị sau trong phương trình 2:
PV = $5,000,000
r = 7% = 0,7
N=5
FVN = PV(1 + r)N
= $5,000,000(1.07)5
= $5,000,000(1.402552)


= $7,012,758.65
Vào cuối năm thứ năm, bạn sẽ có $7,012,758.65 nếu nếu tiền của bạn vẫn được giữ

lại để đầu tư ở mức lãi suất 7%/năm mà khơng có rút tiền.
Trong hầu hết các ví dụ trong bài đọc, lưu ý rằng các hệ số được ghi lại sáu chữ số
thập phân, nhưng các tính tốn thực sự có thể phản ánh độ chính xác cao hơn. Ví dụ,
số 1.402552 đã được làm trịn từ 1.40255173 (hiện nay tính tốn với hơn tám chữ số
thập phân của độ chính xác được thực hiện bằng máy tính hoặc bảng tính). Kết quả
cuối cùng của chúng tôi phản ánh số chữ số thập phân cao hơn được thực hiện bởi
máy tính hoặc bảng tính3.
3

Chúng ta cũng có thể giải quyết vấn đề giá trị thời gian của tiền bằng bảng các hệ

số lãi suất. Giải pháp sử dụng bảng các hệ số lãi suất nói chung là ít chính xác hơn
các kết quả thu được bằng cách sử dụng máy tính hoặc bảng tính, do đó, những
người thực hành thích máy tính hoặc bảng tính hơn.
VÍ DỤ 2
Giá trị tương lai của một khoản tiền trả một lần mà khơng có tiền mặt tạm thời
Một định chế đưa ra đề nghị với bạn trong một hợp đồng với bộ ba điều khoản sau: đối
với một khoản đầu tư ¥ 2.500.000 định chế hứa hẹn sẽ trả cho bạn một lần trong sáu năm
kể từ bây giờ ở mức lãi suất 8% hàng năm. Số tiền trong tương lai bạn có thể nhận được?
Giải pháp: sử dụng các dữ liệu sau đây trong phương trình 2 để tìm giá trị tương lai:
PV = ¥2,500,000
r = 8% = 0.08
N=6
FVN = PV(1 + r)N
= ¥2,500,000(1.08)6
= ¥2,500,000(1.586874)


= ¥3,967,186
Bạn có thể mong đợi để nhận ¥ 3.967.186 sau sáu năm kể từ bây giờ.

Ví dụ thứ ba của chúng ta là một vấn đề phức tạp hơn về giá trị trong tương lai để minh
họa tầm quan trọng của việc theo dõi đúng lịch thời gian.
VÍ DỤ 3
Giá trị tương lai của một khoản tiền trả một lần
Một nhà quản lý quỹ hưu trí ước tính rằng cơng ty tài trợ của ơng sẽ đóng góp 10 triệu $
trong năm năm tới. Tỷ lệ lợi tức trong kế hoạch tài sản đã được ước tính ở mức 9% mỗi
năm. Người quản lý quỹ hưu trí muốn tính tốn giá trị tương lai của khoản đóng góp này
trong 15 năm kể từ bây giờ, đó là ngày mà các quỹ sẽ được phân phối cho người về hưu.
Giá trị trong tương lai là gì?
Giải pháp: bằng cách định vị giá trị đầu tư ban đầu, PV, tại t = 5, chúng ta có thể tính tốn
giá trị tương lai của sự đóng góp bằng cách sử dụng các dữ liệu sau đây trong phương
trình 2:
PV = 10 triệu $
r = 9% = 0.09
N = 10
FVN = PV(1+ r)N
= $10,000,000(1.09)10
= $10,000,000(2.367364)
= $ 23,673,636.75
Vấn đề này trông giống như hai ví dụ trước, nhưng nó khác nhau ở một khía cạnh quan
trọng: thời gian của nó. Từ quan điểm của ngày hôm nay (t = 0), lượng tiền tương lai
$23,673,636.75 là sau 15 năm trong tương lai. Mặc dù giá trị tương lai là 10 năm kể từ


giá trị hiện tại của nó, giá trị hiện tại của 10 triệu $ sẽ không được nhận trong năm năm
nữa.
Hình 2 Giá trị tương lai của khoản tiền trả một lần, đầu tư ban đầu không phải tại t = 0

Như hình 2 cho thấy, chúng tơi đã theo các quy ước kí hiệu ngày hơm nay là t = 0 và kí
hiệu các khoảng thời gian tiếp theo bằng cách cộng 1 cho từng kỳ. Khoản đóng góp thêm

10 triệu $ là nhận được trong năm năm, do đó, nó được kí hiệu tại t = 5 và xuất hiện như
trong hình. Giá trị tương lai của đầu tư trong 10 năm sau đó được kí hiệu tại t = 15, có
nghĩa là, 10 năm sau khi nhận được sự đóng góp 10 triệu $ tại t = 5. Dịng thời gian như
thế này có thể cực kỳ hữu ích khi đối phó với vấn đề phức tạp hơn, đặc biệt là những vấn
đề liên quan đến nhiều hơn một dòng tiền.
Trong phần sau của bài đọc này, chúng ta sẽ thảo luận làm thế nào để tính tốn giá trị
hơm nay của 10 triệu $ được nhận sau năm năm kể từ bây giờ. Đến thời điểm này, chúng
ta có thể sử dụng phương trình 2. Giả sử người quản lý quỹ hưu trí ở Ví dụ 3 trên đây đã
được nhận $6,499,313.86 hôm nay từ nhà tài trợ của cơng ty. Số tiền đó sẽ có giá trị bao
nhiêu vào cuối năm năm? Nó sẽ có giá trị bao nhiêu vào cuối 15 năm?
PV = $6, 499,313.86
r = 9% = 0.09
N=5
FVN = PV(1 + r)N
= $6,499,313.86(1.09)5


= $6,499,313.86(1.538624)
= $10,000,000 tại mốc 5 năm
Và
PV = $6,499,313.86
r = 9% = 0.09
N = 15
FVN = PV(1 + r)N
= $6, 499,313.86(1.09)N
= $6, 499,313.86(3.642482)
= $23,673,636.74 tại mốc 15 năm
Những kết quả này chỉ ra rằng làm thế nào mà giá trị hiện tại của ngày hôm nay khoảng
6,5 triệu $ trở thành 10 triệu $ sau 5 năm và 23,67 triệu $ sau 15 năm.

3.1 Tần số của lãi kép
Trong phần này, chúng tôi xem xét việc đầu tư mà trả lãi nhiều hơn một lần một năm. Ví
dụ, nhiều ngân hàng đề nghị một tỷ lệ lãi suất hàng tháng để mà ghép lãi 12 lần một năm.
Theo thỏa thuận như vậy, họ phải trả lãi trên lãi mỗi tháng. Thay vì báo tỷ lệ lãi suất định
kỳ hàng tháng, các định chế tài chính thường báo một mức lãi suất hàng năm mà chúng
tôi gọi là lãi suất công bố hàng năm hoặc lãi suất công bố. Chúng tôi biểu thị mức lãi suất
công bố hàng năm bằng rs. Ví dụ, ngân hàng của bạn có thể để cho một CD đặc biệt được
trả 8% lãi ghép hàng tháng. Lãi suất công bố hàng năm bằng lãi suất hàng tháng nhân với
12.4 Tỷ lệ này là một quy ước định giá một cách chặt chẽ bởi vì (1 + 0,0067)12 = 1.083,
chứ không phải 1.08; số hạn (1 + rs) khơng có nghĩa là một hệ số giá trị tương lai khi lãi
kép thì được trả thường xuyên hơn so với hàng năm.
Với nhiều hơn một thời kỳ lãi kép mỗi năm, cơng thức giá trị tương lai có thể được thể
hiện như


FVN = PV (1 + )mN
Trong đó rs là lãi suấtcông bố hàng năm đã nêu, m là số kỳ lãi kép mỗi năm, và N bây giờ
là viết tắt của số năm. Lưu ý ở đây sự phù hợp giữa lãi suất được sử dụng, r s / m, và số kỳ
lãi kép, mN. Tỷ lệ định kỳ, rs / m, là lãi suất được công bố hàng năm chia cho số kỳ lãi
kép mỗi năm. Số lượng các kỳ lãi kép, mN, là số kỳ lãi kép trong một năm nhân với số
năm. Tỷ lệ định kỳ, rs/ m, và số lượng thời kỳ lãi kép, mN, phải tương thích.
VÍ DỤ 4
Giá trị tương lai của khoản tiền trả một lần với lãi kép hàng quý
Tiếp tục với các ví dụ CD, giả sử ngân hàng cung cấp cho bạn một CD với thời hạn hai
năm, tỷ lệ lãi suất công bố hàng năm 8% lãi ghép hàng quý và đặc biệt cho phép tái đầu
tư ở cùng mức lãi suất, bạn quyết định đầu tư $10,000. CD sẽ có giá trị bao nhiêu khi đến
hạn?
4

Để tránh các lỗi làm trịn số khi sử dụng máy tính tài chính, chia 8 cho 12 sau đó nhấn

%i phím, thay vì chỉ là nhập đơn giản 0,67%, vì vậy chúng tơi có (1 + 0,08/12)12 =
1,083000
Giải pháp: tính tốn giá trị trong tương lai với phương trình 3 như sau:
PV = $10,000
rs = 8% = 0.08
m=4
rs/ m = 0.08/4 = 0.02
N=2
mN = 4(2) = 8 thời kì lãi suất

FVN = PV (1 + )mN
= $10,000(1.02)8


= $10,000(1.171659)
= $11,716.59
Lúc đến hạn, CD sẽ có giá trị $11,716.59.
Cơng thức giá trị tương lai trong phương trình 3 khơng khác cơng thức giá trị
tương lai trong phương trình 2. Đơn giản là chỉ cần nhớ rằng lãi suất sử dụng là lãi
suất mỗi thời kì và số mũ là số thời kì của lãi suất hay lãi kép.
VÍ DỤ 5
Giá trị tương lai của một khoản tiền trả một lần với lãi kép hàng tháng
Một ngân hàng Úc đề nghị trả cho bạn 6% lãi kép hàng tháng. Bạn quyết định đầu tư 1
triệu $ Úc cho một năm. Giá trị tương lai của số tiền đầu tư của bạn là bao nhiêu nếu
thanh toán lãi được tái đầu tư ở mức 6%?
Giải quyết: sử dụng phương trình 3 để tìm giá trị tương lai của khoản đầu tư một năm
như sau:
PV = A$1,000,000
rs= 6% = 0.06

m = 12
rs/ m = 0.06/12 = 0.0050
N=1
mN = 12(1) = 12 thời kỳ lãi suất

FVN = PV (1 + )mN
= $A1,000,000(1.005)12
= $A1,000,000(1.061678)
= $A1,061,677.81


Nếu bạn được trả 6% với lãi kép hàng năm, số tiền trong tương lai sẽ chỉ là A$1.000.000
(1,06) = A$1.060.000 thay vì A$1,061,677.81 với lãi kép hàng tháng.
3.2 Lãi kép liên tục
Cuộc thảo luận trước về kỳ lãi kép minh họa cho lãi kép rời rạc, có nghĩa là lãi suất tín
dụng sau một lượng thời gian rời rạc đã trôi qua. Nếu số kỳ lãi kép mỗi năm trở nên vơ
hạn, thì khi đó lãi được gọi là lãi kép liên tục. Nếu chúng ta muốn sử dụng công thức giá
trị tương lai với lãi kép liên tục, chúng ta cần phải tìm các giá trị giới hạn của hệ số giá trị
tương lai tức là cho m → ∞ (kỳ lãi kép nhiều vô hạn mỗi năm) trong phương trình 3.
Biểu thị cho giá trị tương lai của một khoản tiền trong N năm với lãi kép liên tục là:

FVN = PV
Hệ số là số siêu việt e ≈ 2.7182818 mũ rsN. Hầu hết các máy tính tài chính có
chức năng ex.
VÍ DỤ 6
Giá trị tương lai của một khoản tiền trả một lần với lãi kép liên tục
Giả sử một khoản đầu tư $10,000 sẽ thu được 8% lãi kép liên tục trong 2 năm. Chúng
ta có thể tính tốn giá trị tương lai với phương trình 4 như sau:
PV = $10,000
rs= 8% = 0.08

N=2

FVN = PV
= $10,000e0.08(2)
= $10,000(1.173511)
= 11,735.11


Với mức lãi suất tương tự nhưng sử dụng lãi kép liên tục, khoản đầu tư $10.000 sẽ
tăng đến $11,735.11 trong hai năm, so với $11,716.59 bằng cách sử dụng lãi ghép
hàng quý như trong Ví dụ 4.
Như bảng 1 cho thấy, tất cả sáu trường hợp có cùng mức lãi suất cơng bố hàng năm là
8%, chúng có sự khác nhau về số lượng đô la cuối cùng, tuy nhiên, bởi vì sự khác biệt
tần số lãi kép. Với lãi kép hàng năm, số lượng cuối cùng là $1,08. Lãi ghép càng
thường xuyên kết quả là số tiền cuối cùng càng lớn. Số lượng $ cuối cùng với lãi kép
liên tục là số tiền tối đa mà có thể thu được với tỷ lệ lãi suất công bố hàng năm 8%.
Bảng 1 Ảnh hưởng của tần số lãi kép lên giá trị tương lai
Tần số

rs/ m

mN

Hàng năm
Bán niên

8% / 1 = 8%
8% / 2 = 4%

1×1=1

2×1=2

Hàng quý

8% / 4 = 2%

4×1=4

Hàng tháng

8% / 12 = 0.6667%

12 × 1 = 12

Hàng ngày

8% / 365 = 0.0219
%

365 × 1 = 365

Liên tục

Giá trị tương lai của
$1
$1.00(1.08) = $1.08
$1.00(1.04)2 =
$1.081600
$1.00(1.02)4 =
$1.082432

$1.00(1.006667)12 =
$1.083000
$1.00(1.000219)365
= $1.083278
$1.00e0.08(1) =
$1.083287

Bảng 1 cũng chỉ ra rằng khoản đầu tư $1 thu được 8.16% lãi ghép hàng năm tăng lên
giống với giá trị tương lai lúc cuối một năm như khoản đầu tư 1$ thu được 8% lãi
ghép nữa năm. Kết quả này dẫn chúng ta đến một sự phân biệt giữa lãi suất công bố
hàng năm và lãi suất thực hàng năm (EAR)5. Đối với 8% lãi suất công bố hàng năm
với lãi ghép bán niên, EAR là 8.16%.
3.3 lãi suất công bố và lãi suất hiệu quả
Lãi suất công bố hàng năm không đưa ra một giá trị trong tương lai trực tiếp, vì vậy
chúng ta cần một công thức cho EAR. Với mức lãi suất công bố hàng năm là 8% lãi
ghép bán niên, chúng ta nhận được một tỷ lệ lãi suất định kỳ 4%. Trong suốt quá trình


một năm, một khoản đầu tư $1 sẽ tăng lên $1(1.04)2 = $1.0816, như minh họa trong
Bảng 1. Tiền lãi thu được trên khoản đầu tư $1 là $0,0816 và tương ứng với một tỷ lệ
lãi suất thực hàng năm 8.16%. Tỷ lệ lãi suất thực hàng năm được tính như sau:

EAR = (1 + tỷ lệ lãi suất định kì)m – 1
Tỷ lệ lãi suất định kỳ là tỷ lệ lãi suất công bố hàng năm chia cho m, trong đó mà số
thời kỳ lãi kép trong một năm. Sử dụng ví dụ trước, chúng ta có thể giải ra EAR như
sau: (1.04)2 -1 = 8.16 %
Khái niệm về EAR mở rộng cho lãi kép liên tục. Giả sử chúng ta có tỷ lệ lãi kép liên
tục 8%. Chúng ta có thể tìm ra EAR tương tự như trên bằng cách tìm ra hệ số giá trị
tương lai tương ứng. Trong trường hợp này, một khoản đầu tư $1 sẽ tăng lên đến $1e
0,08(1.0)

= $1,0833. Lãi thu được trong một năm tương ứng với một lãi suất hiệu quả

hàng năm là 8,33% và lớn hơn EAR 8,16% với lãi ghép bán niên bởi vì lãi suất được
ghép thường xuyên hơn. Với lãi kép liên tục, chúng ta có thể giải ra tỷ lệ lãi suất thiệu
quả hàng năm như sau:

EAR = - 1
Chúng ta có thể giữ lại các công thức cho EAR với lãi kép rời rạc và liên tục để tìm ra
một lãi suất định kỳ mà nó tương ứng với một lãi suất hiệu quả cụ thể hàng năm. Giả
sử chúng ta muốn tìm ra tỷ lệ lãi suất định kỳ tương ứng cho một tỷ lệ lãi suất hiệu
quả hàng năm cho trước 8,16% với lãi ghép bán niên. Chúng ta có thể sử dụng
phương trình 5 để tìm ra tỷ lệ lãi suất định kỳ:

0.0816 = (1 + lãi suất định kì)2 – 1
1.0816 = (1 + lãi suất định kì)2
(1.0816)1/2 – 1 = lãi suất định kì
(1.04) – 1 = lãi suất định kì


4% = lãi suất định kì
Để tính lãi kép liên tục (lãi suất công bố hàng năm với lãi kép liên tục) tương
ứng với lãi suất hiệu quả 8.33%, chúng ta thấy lãi suất này thỏa mãn phương
trình 6:
0.0833 = - 1

1.0833 =
Để giải quyết phương trình này, chúng ta lấy logarit tự nhiên của cả hai bên. (Nhớ lại
rằng log tự nhiên của là ln = rs. .) Vì vậy, ln1.0833 = rs, kết quả là rs = 8%. Chúng
ta thấy rằng lãi suất công bố hàng năm là 8% với lãi kép liên tục thì tương đương với

EAR 8,33%.