Đồ án:" Bài toán điều khiển vị trí của đầu đọc ghi " doc

z














Đồ án
Bài toán điều khiển
vị trí của đầu đọc ghi

MỤC LỤC
CHƯƠNG 1: XÂY DỰNG MÔ HÌNH BÀI TOÁN 2
1.1. ĐẶT VẤN ĐỀ 2
1.1.1. Mục đích 2
1.1.2. Yêu cầu 2
1.2. PHÂN TÍCH CÁC THÀNH PHẦN LỰC CỦA BÀI TOÁN 4
1.3. XÂY DỰNG MÔ HÌNH TOÁN 6
1.3.1. Phương trình vi phân 6
1.3.2. Hàm truyền 6
Thay số ta có: 7
1.3.3. Không gian trạng thái 8
1.3.4. Mô hình hóa bằng phương pháp tương tự 9
CHƯƠNG 2: TỔNG HỢP BỘ ĐIỀU KHIỂN 11
2.1. PHƯƠNG PHÁP QUỸ TÍCH NGHIỆM 11
2.1.1. Cực của hệ kín 11
2.1.2. Các bước tổng hợp bộ điều khiển 12
2.1.3. Bộ bù Lead 12
2.2. TỔNG HỢP BỘ ĐIỀU KHIỂN 13
2.3. MÔ PHỎNG HỆ THỐNG DÙNG SIMULINK 20
CHƯƠNG 3: KẾT LUẬN VÀ KIẾN NGHỊ 22
3.1. KẾT LUẬN 22
3.2. KIẾN NGHỊ 22
TÀI LIỆU THAM KHẢO 23
PHỤ LỤC 23

CHƯƠNG 1: XÂY DỰNG MÔ HÌNH BÀI TOÁN
1.1. ĐẶT VẤN ĐỀ
Trong ổ đĩa cứng, sự hoạt động của đĩa cứng cần thực hiện đồng thời hai
chuyển động: chuyển động quay của các đĩa và chuyển động của các đầu đọc.
Chuyển động quay của các đĩa từ được thực hiện nhờ các động cơ gắn cùng
trục (với tốc độ rất lớn: từ 3600 rpm cho đến 15.000 rpm) chúng thường được quay
ổn định tại một tốc độ nhất định theo mỗi loại ổ đĩa cứng.
Khi đĩa cứng quay đều, đầu đọc sẽ di chuyển đến các vị trí trên các bề mặt
chứa phủ vật liệu từ theo phương hướng kính của đĩa. Chuyển động này kết hợp
với chuyển động quay của đĩa có thể làm đầu đọc/ghi tới bất kỳ vị trí nào trên bề
mặt đĩa để đọc/ghi dữ liệu.
Bài toán đưa ra trong đồ án là bài toán điều khiển vị trí của đầu đọc ghi.
1.1.1. Mục đích
- Giúp học viên ôn tập lại và bổ sung kiến thức cho các môn học đã được học,
đặc biệt là môn phân tích và tổ hợp hệ thống Cơ điện tử.
- Giúp học viên rèn luyện các kỹ năng liên quan, đồng thời rèn luyện ý thức và
kỹ năng trình bày 1 văn bản khoa học theo tiêu chuẩn phục vụ cho quá trình
làm đồ án tốt nghiệp sắp tới.
1.1.2. Yêu cầu
Yêu cầu của bài toán là khảo sát tính ổn định của hệ thống, từ đó tổng hợp
bộ điều khiển theo phương pháp quỹ tích để điều khiển vị trí của đầu đọc/ ghi
(tương đương với điều khiển góc
L

). Muốn vậy ta cần phải nghiên cứu những vấn
đề sau:
- Nghiên cứu động học, động lực học của hệ thống. Từ đó xác định được hàm
truyền và mô hình hóa của hệ thống. Khảo sát tính ổn định và chất lượng
của hệ thống.
- Tổng hợp bộ điều khiển thích hợp cho hệ thống sử dụng phương pháp quỹ

tích nghiệm.
Bảng tham số
Ki
Hằng số mô men [Nm/A]
10
Kb
Hằng số điện động cơ [V/rad/sec]
0.0706
Bm
Hệ số ma sát động cơ [Nm/rad]
3
Ra
Điện trở phần ứng
0.25
La
Điện cảm
0
K
L
Hệ số căng [Nm/rad]
2000
B
L
Hệ số ma sát giữa dây đai và puli [Nm/rad/s]
10
Jm
Mô men quán tính động cơ [Nm/rad/s
2
]
0.002

J
L
Mô men quán tính tải [Nm/rad/s
2
]
3
Yêu cầu:
- Thời gian tăng <=0.3s
- Thời gian quá độ <=1s
- Độ quá chỉnh<5%
1.2. PHÂN TÍCH CÁC THÀNH PHẦN LỰC CỦA BÀI TOÁN
Hệ thống gồm có các thành phần:
- Động cơ điện một chiều điều khiển bằng điện áp đặt lên cuộn dây phần ứng.
- Bộ truyền đai (Puli – dây đai).
Ta mô hình hóa hệ thống như sau:
Hình 1: Mô hình động cơ điện 1 chiều ACM
Bộ truyền đai được mô hình hóa bằng 1 giảm chấn xoắn và 1 lò xo xoắn với
các hệ số B
L
, K
L.
Khi Puly quay 1 góc

thì sẽ sinh ra mômen ma sát T
ms
và
mômen do lực căng T
c
.( Hình 2)
Hình 2: Các mômen sinh ra khi Puly quay

Ta có mô hình của hệ thống Puli – dây đai như sau:
Hình 3: Mô hình bộ truyền Puli – dây đai
 Tác dung lên Puli 1:
- Mômen dẫn động T
0
truyền từ trục động cơ điện.
- Mômen quán tính :
1qt m m
T J



- Mômem ma sát nhớt:
1
( )
ms L m L
T B
 
 
 
- Mômen do lực căng đai gây ra:
1
( )
c L m L
T K
 
 
 Tác dung lên Puli 2:
- Mômen quán tính :
2

.
qt L L
T J



- Mômem ma sát nhớt:
2
( )
ms L L m
T B
 
 
 
- Mômen do lực căng đai gây ra:
1
( )
c L L m
T K
 
 
 Phương trình cân bằng mômen của hệ thống :
0 1 1 1
2 2 2
0
qt ms c
qt ms c
T T T T
T T T
  




  



0
( ) ( )
( ) ( ) 0
m m L m L L m L
L L L L m L L m
T J B K
J B K
    
    

    


    


  
  
1.3. XÂY DỰNG MÔ HÌNH TOÁN
1.3.1. Phương trình vi phân
Ta có hệ phương trình vi phân của hệ thống như sau:
( ) ( )
( ) ( ) 0

a a
R L a
m m m m L m L L m L m
L L L L m L L m
e e e e
J B B K T
J B K
     
    
  


     


    

   
  
( ) ( )
( ) ( ) 0
a
b m a a a a
m m m m L m L L m L i a
L L L L m L L m
di
K R i L e
dt
J B B K K i
J B K


     
    

  



      


    




   
  
Vì L
a
=0 cho nên ta có:
( ) ( )
( ) ( ) 0
b m a a a
m m m m L m L L m L i a
L L L L m L L m
K R i e
J B B K K i
J B K


     
    

 

      


    


   
  
1.3.2. Hàm truyền
Biến đổi Laplace hệ phương trình (1) ta có:
2
2
( ) ( )
( ) ( ) 0
b m a a a
m m L L m L L L i a
L L L L L L m
K s R I E
J s B s B s K B s K K I
J s B s K B s K

  


       



      


(1)
2
2
( ) ( )
( ) ( ) 0
a b m
a
a
a b m
m m L L m L L L i
a
L L L L L L m
E K s
I
R
E K s
J s B s B s K B s K K
R
J s B s K B s K

 






 

        



      




2
2
( ) ( )
( ) ( ) 0
a m m L L m a L L L i a b m
L L L L L L m
R J s B s B s K R B s K K E K s
J s B s K B s K

 
         
 


 


      


2
2
( ) ( )
( ) ( ) 0
a m m L L i b m a L L L i a
L L m L L L L
R J s B s B s K K K s R B s K K E
B s K J s B s K

 
        

 


       


 
2 2 2
( ) ( ) ( )
( )
a m m L L i b L L L a L L L
L L i a
R J s B s B s K KK s J s B s K R B s K
B s K KE
 
         
 

 
2 2 2
( )
( ) ( ) ( )
L
a
L L i
a m m L L i b L L L a L L
TF
E
B s K K
R J s B s B s K K K s J s B s K R B s K

  


 
       
 
Thay số ta có:
4 3 2
100 20000
0.0015 11.87 1516 2912
s
TF
s s s s


  
(2)

1.3.3. Không gian trạng thái
Từ hệ phương trình (1) ta có:
( ) ( )
( ) ( ) 0
a b m
m m m m L m L L m L i
a
L L L L m L L m
e K
J B B K K
R
J B K

     
    


     




    


   
  
1 1 1 1 1
( )
i b i a

m m L m L L L m L L
m a m m m m a
L L L L
L m L m L
L L L L
K K K E
B B B K K
J R J J J J R
B B K K
J J J J
    
    

       





   


  
  
Đặt biến trạng thái:
1 2 3 4
( , , , ) ( , , , )
m L m L
x x x x
   


 
Khi đó ta có:
1 3
2 4
3 1 2 3 4
4 1 2 3 4
1 1
( ) .
L L i b L i a
m L
m m m a m m a
L L L L
L L L L
x x
x x
K K KK B KE
x x x B B x x
J J J R J J R
K K B B
x x x x x
J J J J






      




   






3
1
2
1
2
3
3
4
0
0 0
0 1 0
. .
0
0 1
0
1
( )
1
.
0
i b

L L L
m L
i
m m m a m
m a
L L L L
L L L L
a
KK
K K B
B B
K
J J J R J
J R
K K B B
J J J J
x
x
x
x
E
x
x
x
x
 
 
 
 
 

 
 
 
 
 
 
 
 
 
  
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
   
 





Đầu ra:
1
2
2
3
3
[0 1 0 0]
L
x
x
x
x
x

 
 
 
 






1.3.4. Mô hình hóa bằng phương pháp tương tự
Ta có sơ đồ tương đương của hệ thống.
Hình 4: Sơ đồ tương đương của hệ thống
Đặt PV: điện áp hoặc vận tốc góc
FV: dòng điện hoặc mômen

Ta có sơ đồ trở kháng
Hình 5: Sơ đồ trở kháng của hệ thống
Từ sơ đồ trở kháng ta có các phương trình điểm nút như sau:
1
2 21 22 23
3 2 23.
1 . 2
2 . 1
3 23.
L
L
Ra
BK
b
i
J
PVa PV PV
FV FV FV FV
PV PV FV Z
PV K PV
FV K FV
PV FV Z
 
  
 



Ta các phương trình trên ta có sơ đồ khối như sau:
Hình 6: Sơ đồ khối của hệ thống

CHƯƠNG 2: TỔNG HỢP BỘ ĐIỀU KHIỂN
2.1. PHƯƠNG PHÁP QUỸ TÍCH NGHIỆM
Mục đích của việc thiết kế quỹ tích nghiệm là ước đoán đáp ứng của hệ kín
thông qua quỹ tích nghiệm của hệ hở. Bằng cách thêm vào hệ thống các điểm
không và điểm cực (thêm khâu bù), quỹ tích nghiệm và đáp ứng của hệ kín sẽ được
điều chỉnh theo ý muốn.
2.1.1. Cực của hệ kín
Quỹ tích nghiệm (mạch hở) của một hàm truyền H(s) là đồ thị thể hiện vị trí
của tất cả các cực của hệ kín với hệ số tỷ lệ K và phản hồi đơn vị:
Hàm truyền mạch kín với phản hồi đơn vị bằng:
( ) ( )
( ) 1 ( )


Y s KH s
R s KH s
Cực của hệ kín là các giá trị, sao cho
1 ( ) 0 KH s
.
Nếu viết
( )
( )
( )

b s
H s
a s
, thì phương trình có dạng:
( ) ( ) 0
( )

( ) 0
 
 
a s Kb s
a s
b s
K
Gọi n là bậc của đa thức a(s) và m là bậc của đa thức b(s).
Tại giới hạn K -> 0, cực của hệ kín ứng với a(s) = 0 hoặc cực của H(s). Tại
giới hạn K -> vô cùng, cực của hệ kín ứng với b(s) = 0 hoặc điểm 0 của H(s). Dù K
ứng với điểm nào đi nữa thì hệ kín cũng phải luôn luôn có n cực, trong đó n chính
là số cực của H(s). Đường quỹ tích phải có n nhánh, mỗi nhánh xuất phát từ cực
của H(s) và chạy đến điểm 0 của H(s). Nếu H(s) có số cực nhiều hơn số điểm 0
(điều thường xảy ra), m < n thì ta nói rằng H(s) có điểm 0 ở vô cùng. Trong trường
hợp này, giới hạn của H(s) khi s -> vô cùng bằng 0. Số điểm 0 ở vô cùng là hiệu
n-m, nghĩa là hiệu giữa số cực và số điểm 0 và là số nhánh của quỹ tích nghiệm
tiến tới vô cùng (tiệm cận).
Vì quỹ tích nghiệm biểu diễn mọi vị trí có thể của các cực của hệ kín, nên từ
quỹ tích nghiệm chúng ta có thể chọn hệ số truyền để đạt các tính năng đặt ra cho
hệ thống. Nếu có bất kỳ một cực nào nằm trong nửa mặt phẳng phía phải thì hệ kín
sẽ không ổn định. Cực càng nằm ở gần trục ảo thì ảnh hưởng càng nhiều đến đáp
ứng hệ kín.
2.1.2. Các bước tổng hợp bộ điều khiển
Các bước tổng hợp bộ điều khiển bằng phương pháp quỹ tích nghiệm:
- Bước 1: Vẽ quỹ tích nghiệm của hệ hở dùng lệnh rlocus trong Matlab.
- Bước 2: Chọn hệ số tỉ lệ K từ quỹ tích nghiệm
- Bước 3: Kiểm tra và so sánh với các chỉ tiêu đặt ra (sai số xác lập, độ quá
điều chỉnh, thời gian quá độ). Nếu chưa đạt yêu cầu thì thử lại giá trị K.
- Bước 4: Nếu không có giá trị K thỏa mãn thì thêm bộ bù lead-lag để điều
chỉnh.

2.1.3. Bộ bù Lead
Một bộ bù lead bậc 1 có thể được thiết kế sử dụng cho quỹ tích nghiệm. Một
bộ bù lead trong quỹ tích nghiệm có dạng:
0
0
( )
c
s z
G s K
s p



Trong đó, giá trị z
0
nhỏ hơn giá trị p
0
. Một bộ bù lead làm cho quỹ tích
nghiệm dịch chuyển về nửa mặt phẳng trái. Điều này cải thiện tính ổn định và tăng
tốc độ đáp ứng của hệ thống.
Biểu thức để xác định giao điểm của đường tiệm cận với trục thực là:
( ) ( er )
(# ) (# er )
poles z o
poles z os




 

Khi một bộ bù lead được thêm vào hệ thống, giá trị của giao điểm này sẽ là
một số âm lớn hơn giá trị trước đó. Số điểm 0 và số điểm cực sẽ giống nhau (một
điểm 0 và một điểm cực được thêm vào). Nhưng điểm cực được thêm vài là một số
âm lớn hơn điểm 0 được thêm vào. Vì thế, hiệu quả của bộ bù lead là làm dịch
chuyển giao điểm của tiệm cận xa hơn về nửa mặt phẳng trái, và toàn bộ quỹ tích
nghiệm được dịch chuyển về phía trái, Điều này làm tăng vùng ổn định cũng như
tốc độ đáp ứng của hệ thống.
2.2. TỔNG HỢP BỘ ĐIỀU KHIỂN
a. Quỹ tích nghiệm của hệ hở:
Tạo 1 m-file với các lệnh sau để lập mô hình hệ hở và vẽ quỹ tích nghiệm.
Ki=10;
Kb=0.0706;
Bm=3;
Ra=0.25;
Kl=2000;
Bl=10;
Jm=0.002;
Jl=3;
rtime=0.3;
Tr=1;
Mp=5;
num=[Bl Kl]*Ki;
den=conv(Ra*[Jm Bm+Bl Kl]+[0 Ki*Kb 0],[Jl Bl Kl])-Ra*[0 0 Bl*Bl 2*Bl*Kl
Kl*Kl];
sys1=tf(num,den)
rlocus(sys1)
Chạy m-file ta sẽ có quỹ tích nghiệm như sau:
Hình 7: Quỹ tích nghiệm của hệ thống
Tiêu chuẩn ổn định được biểu diễn bằng lệnh sgrid(zeta,Wn).
Trong đó: zeta, Wn lần lượt là hệ số giảm chấn và tần số dao động

riêng được xác định theo công thức (3) với Tr là thời gian quá độ,
P
M
là độ quá
điều chỉnh.
1.8
Wn
Tr

;
2
2
ln( )
ln( )
1
P
P
M
zeta
M


 
 
 

 

 
 

Thêm tiếp các lệnh sau vào m-file:
Wn=1.8/Tr
zeta=sqrt(((log(Mp)/pi)^2)/(1+(log(Mp)/pi)^2))
sgrid(zeta, Wn)
(3)
Nhìn vào tỉ lệ xích của các trục ta thấy có 1 điểm cực ở rất xa về phía trái (xa
hơn -7,79x10
3
). Điểm cực này không ảnh hưởng tới quá trình động lực học của hệ
kín trừ khi ta sử dụng các hệ số rất lớn, ở đó hệ thống trở nên mất ổn định. Chúng
ta bỏ qua điểm cực này và thực hiện tối giản hoá mô hình hệ thống.
b. Tối giản hóa mô hình
Để xem các điểm cực của hàm truyền là gì, gọi lệnh sau trong Matlab:
roots(den)
Ta có kết quả sau:
poles =
1.0e+003 *
0
-7.7856
-0.1278
-0.0020
Ta muốn bỏ qua điểm cực -7,7856.10
3
. Thực hiện điều này bằng đoạn lệnh
sau:
den2=deconv(den,[1/max(abs(poles)) 1]);
sys2=tf(num,den2);
roots(den2);
Bây giờ ta vẽ quỹ đạo nghiệm của hệ đã được tối giản. Thêm những lệnh sau
vào m-file trên.

rlocus(sys2)
sgrid(zeta,Wn)
Hình 8: Quỹ tích nghiệm của hệ thống sau khi tối giản hóa mô hình
Từ quỹ đạo vẽ được, ta thấy hệ thống không ổn định vì có 1 phần quỹ đạo
nghiệm nằm ở nửa mặt phẳng bên trái. Để hệ thống ổn định, ta cần dịch chuyển
quỹ đạo nghiệm sang nửa mặt phẳng bên trái. Để làm điều đó, ta sẽ sử dụng bộ bù
Lead.
c. Bộ bù Lead
Một khâu Lead có hàm truyền như sau:
0
0
W( )
s z
p
s p



Ta sẽ đặt một điểm không ở gần gốc toạ độ để khử đi một cực. Cực của khâu
bù sẽ được đặt ở phía bên trái gốc toạ độ để kéo quỹ tích nghiệm về phía trái mặt
phẳng toạ độ. Thêm các lệnh sau vào m-file.
zo = 4;
po = 70;
lead=tf([1 zo],[1 po]);
sys3=lead*sys2
rlocus(sys3)
sgrid(zeta, Wn)
Ta có quỹ tích nghiệm như sau:
Hình 9: Quỹ tích nghiệm của hệ thống với bộ điều khiển Lead
Ta lựa chọn đoạn quỹ tích nghiệm có giá trị nhỏ

axis ([-100 10 -70 70])
Hình 10: Quỹ tích nghiệm của hệ thống với bộ điều khiển Lead
d. Chọn hệ số K
Dùng lệnh rlocfind để chọn hệ số K. Thêm các lệnh sau vào m-file:
[k,poles]=rlocfind(sys3)
Chạy chương trình ta thu được kết quả như sau:
k =
34.6211
poles =
1.0e+002 *
-1.3039
-0.5998
-0.0469 + 0.0088i
-0.0469 - 0.0088i
e. Vẽ đáp ứng của hệ kín
Thêm các lệnh sau vào m-file:
sys_cl= feedback(k*sys3,1);
t=0:0.01:5;
step(sys_cl,t)
Hình 11: Đáp ứng của hệ kín
Ta kiểm tra lại đáp ứng của hệ thống với hàm truyền ban đầu (không bỏ qua
1 điểm cực)
sys_cl1= feedback(k*lead*sys1,1);
t=0:0.01:5;
step(sys_cl1,t)
Ta có đáp ứng giống như trên. Như vậy, điểm cực bỏ qua không ảnh hưởng
đến độ ổn định của hệ thống.
Với hệ số K và bộ bù lead đã lựa chọn, hệ thống đạt được các yêu cầu đề ra.
2.3. MÔ PHỎNG HỆ THỐNG DÙNG SIMULINK
Từ sơ đồ khối xây dựng bằng phương pháp tương tự, ta xây dựng được mô

hình hệ thống trong simulink như sau:
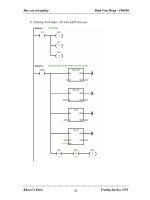
Hình 12: Mô hình hóa hệ thống trong Simulink
Bộ điều khiển được xây dựng như sau:
Hình 13: Hệ kín khi có bộ điều khiển Lead và hệ số K đã chọn
Trước khi chạy file mô phỏng ta phải khai báo các thông số của hệ trong cửa
sổ Matlab như sau:
Ki=10;
Kb=0.0706;
Bm=3;
Ra=0.25;
Kl=2000;
Bl=10;
Jm=0.002;
Jl=3;
Sau khi chạy file mô phỏng ta thu được kết quả như sau:
Hình 14: Đáp ứng của hệ thống
Ta thấy, kết quả mô phỏng trong Simulink tương tự kết quả mô phỏng dùng
m–file.
CHƯƠNG 3: KẾT LUẬN VÀ KIẾN NGHỊ
3.1. KẾT LUẬN
Đồ án đã hoàn thành đúng tiến độ và đầy đủ các nội dung bao gồm:
- Vai trò, ý nghĩa của bài toán.
- Xây dựng mô hình hóa của hệ thống bằng các phương pháp đã được học
- Xây dựng bộ điều khiển bằng phương pháp quỹ tích nghiệm. Bộ điều khiển
được xây dựng đã đáp ứng được yêu cầu của đồ án.
- Mô phỏng hệ thống dung Simulink
3.2. KIẾN NGHỊ
Qua quá trình làm đồ án giúp cho sinh viên vận dụng kiến thức của các môn
học như: phân tích tổ hợp hệ thống cơ điện tử, lý thuyết điều khiển tự động, cơ lý
thuyết… Em đã hoàn thành các yêu cầu đề ra.Tuy nhiên đồ án dừng lại ở xây dựng

bộ điều khiển và khảo sát tính ổn định của hệ thống trong môi trường Matlab. Để
xây dựng hệ thống thực tế, ta có thể vẽ mô hình hệ thống bằng phần mềm CAD
3D(Inventor). Sau đó, liên kết giữa mô hình CAD với gói công cụ SimMechanics
trong Matlab để mô phỏng hệ thống.
Do kiến thức còn hạn chế nên đồ án còn nhiều thiếu sót. Vì vậy, em rất mong
nhận được sự chỉ bảo của các thầy. Cuối cùng em xin cảm ơn thầy Hoàng Quang
Chính cùng các thầy trong bộ môn đã giúp đỡ em hoàn thành đồ án này.
TÀI LIỆU THAM KHẢO
1. Bài giảng phân tích và tổ hợp hệ thống cơ điện tử - PGS.TS Đào Văn
Hiệp.
2. Lý thuyết điều khiển tự động - HVKTQS
2. Control Tutorial for Matlab and Simulink
PHỤ LỤC
Chương trình viết bằng Matlab để tổng hợp bộ điều khiển
%%%%%%%%%%%%% Nhập các thông của số hệ thống
Ki=10;
Kb=0.0706;
Bm=3;
Ra=0.25;
Kl=2000;
Bl=10;
Jm=0.002;
Jl=3;
rtime=0.3;
Tr=1;
Mp=5;
%%%%%%%%%%%%% Xây dựng hàm truyền hệ hở
num=[Bl Kl]*Ki;
den=conv(Ra*[Jm Bm+Bl Kl]+[0 Ki*Kb 0],[Jl Bl Kl])-Ra*[0 0 Bl*Bl 2*Bl*Kl
Kl*Kl];

sys1=tf(num,den)
%%%%%%%%%%%%%Quỹ tích nghiệm của hệ hở
rlocus(sys1)
Wn=1.8/Tr
zeta=sqrt(((log(Mp)/pi)^2)/(1+(log(Mp)/pi)^2))
sgrid(zeta, Wn)
% %%%%%%%%%%%Tối giản hóa mô hình
poles=roots(den);
den2=deconv(den,[1/max(abs(poles)) 1]);
sys2=tf(num,den2);
rlocus(sys2)
sgrid(zeta, Wn)
% %%%%%%%%%%%Bộ điều khiển Lead
zo = 3;
po = 70;
lead=tf([1 zo],[1 po]);
sys3=lead*sys2
%%%%%%%%%%%% Lựa chọn hệ số
rlocus(sys3)
sgrid(zeta, Wn)
axis ([-100 10 -70 70])
[k,poles]=rlocfind(sys3)
%%%%%%%%%%%%% Đáp ứng của hệ thống
sys_cl= feedback(k*sys3,1);
t=0:0.01:5;
step(sys_cl,t)
%%%%%%%%%%%% Đáp ứng của hệ thống ban đầu( Ko tối giản hóa mô hình)
sys_cl1= feedback(k*lead*sys1,1);
t=0:0.01:5;
step(sys_cl1,t)