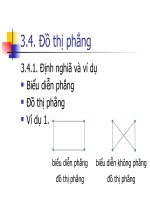
Lý thuyết đồ thị - Phần 1 ppt

Ch ng II. Lý thuy t đ thươ ế ồ ị
I. Các khái niệm cơ bản
II. Biểu diễn đồ thị
III. Tính liên thông
IV. Chu trình Euler
V. Bài toán tìm đường đi ngắn nhất
VI. Đồ thị phẳng
VII.Tô màu đồ thị


I. Các khái ni m c b nệ ơ ả

1. ĐỊNH NGHĨA ĐỒ THỊ (GRAPH)

Là một cấu trúc rời rạc gồm các đỉnh và các cạnh nối các đỉnh
đó. Được mô tả hình thức: G = (V, E)

V gọi là tập các đỉnh (Vertices) và E gọi là tập các cạnh
(Edges). Có thể coi E là tập các cặp (u, v) với u và v là hai
đỉnh thuộc V.

Ví dụ:
Đường
phố
Mạng máy
tính


2. Phân lo i đ thạ ồ ị


G được gọi là đơn đồ thị nếu giữa hai đỉnh phân biệt u,
v của V có nhiều nhất là 1 cạnh trong E nối từ u tới v.

G được gọi là đa đồ thị nếu giữa hai đỉnh phân biệt u, v
của V có thể có nhiều hơn 1 cạnh trong E nối từ u tới v

G được gọi là giả đồ thị nếu G là đa đồ thị và có thể có
cạnh nối từ một đỉnh đến chính nó. Cạnh đó được gọi là
khuyên

G được gọi là đồ thị vô hướng nếu các cạnh trong E
không có sự phân biệt đỉnh nào là đỉnh đầu, đỉnh nào là
đỉnh cuối.

G được gọi là đồ thị có hướng nếu các cạnh trong E có
sự phân biệt đỉnh nào là đỉnh đầu, đỉnh nào là đỉnh cuối.


Ví dụ
Đơn đồ
thị
vô hướng
Đơn đồ
thị
có hướng
Đa đồ thị
vô hướng
Đa đồ thị
có hướng

3. C nh liên thu c, đ nh k , b cạ ộ ỉ ề ậ

Đối với đồ thị vô hướng G = (V, E). Xét một cạnh e ∈ E, nếu
e = (u, v) thì ta nói hai đỉnh u và v là kề nhau (adjacent) và
cạnh e này liên thuộc (incident) với đỉnh u và đỉnh v.

Với một đỉnh v trong đồ thị, ta định nghĩa bậc (degree) của v,
ký hiệu deg(v) là số cạnh liên thuộc với v.

Định lý: Giả sử G = (V, E) là đồ thị vô hướng với m cạnh, khi
đó tổng tất cả các bậc đỉnh trong V sẽ bằng 2m:

Chứng minh: Khi lấy tổng tất cả các bậc đỉnh tức là mỗi cạnh
e = (u, v) bất kỳ sẽ được tính một lần trong deg(u) và một lần
trong deg(v). Từ đó suy ra kết quả.

Hệ quả: Trong đồ thị vô hướng, số đỉnh bậc lẻ là số chẵn
∑
⊂
2=
Vv
m deg(v)



Đối với đồ thị có hướng G = (V, E). Xét một cung e ∈ E, nếu
e = (u, v) thì đỉnh u khi đó được gọi là đỉnh đầu,đỉnh v được
gọi là đỉnh cuối của cung e.


Với mỗi đỉnh v trong đồ thị có hướng, ta định nghĩa: bậc ra
của v ký hiệu deg
+
(v) là số cung đi ra khỏi nó; bậc vào ký hiệu
deg
-
(v) là số cung đi vào đỉnh đó.

Định lý: Giả sử G = (V, E) là đồ thị có hướng với m cung, khi
đó tổng tất cả các bậc ra bằng tổng tất cả các bậc vào và
bằng m:
∑∑
⊂
−
⊂
+
==
VvVv
mvv )(deg)(deg


4. M t s d ng đ th đ c bi tộ ố ạ ồ ị ặ ệ

a. Đồ thị đầy đủ K
n
(n≥1) có n đỉnh và mỗi cặp đỉnh đều có
đúng một cạnh nối.




b. Chu trình C
n
(n≥3) có n đỉnh v
1
,v
2
, v
n
và các cạnh
(v
1
,v
2
); (v
2
,v
3
) (v
n-1
,v
n
) và (v
n
,v
1
)



c. Đồ thị hình bánh xe


Khi thêm một đỉnh vào giữa chu trình C
n
và nối đỉnh này với
các đỉnh của đồ thị C
n
ta thu được đồ thị hình bánh xe.



d. Đồ thị hình khối Q
n
có 2
n

đỉnh, mỗi đỉnh được biểu diễn
bằng xâu nhị phân độ dài n. Hai đỉnh là liền kề nếu các xâu
nhị phân biểu diễn chúng khác nhau đúng một bit.
Q
2
110 111
010
011
001
000
101
100
Q
3


e. Đồ thị phân đôi là đồ thị có tập các đỉnh V có thể phân
làm hai tập con không rỗng, rời nhau V
1
và V
2
sao cho
mỗi cạnh của đồ thị nối 1 đỉnh của V
1
với 1 đỉnh của V
2

Đồ thị phân đôi đầy đủ K
m,n
là đồ thị có tập các đỉnh được
phân thành hai tập con tương ứng có m đỉnh và n đỉnh
và có cạnh giữa hai đỉnh nếu đỉnh thứ nhất thuộc tập
con này, đỉnh thứ hai thuộc tập con kia.


II. Bi u di n đ thể ễ ồ ị
1. Ma trận liền kề (ma trận kề)

Giả sử G = (V, E) là một đơn đồ thị có số đỉnh là n, không
mất tính tổng quát có thể coi các đỉnh được đánh số 1, 2, ,
n. Khi đó ta có thể biểu diễn đồ thị bằng một ma trận vuông
cấp n A = [aij]. Trong đó:

aij= 1 nếu (i, j) ∈ E


aij = 0 nếu (i, j) E∉

Đối với đa đồ thị thì việc biểu diễn cũng tương tự trên, chỉ có
điều nếu như (i, j) là cạnh thì không phải ta ghi số 1 vào vị trí
a
ij
mà là ghi số cạnh nối giữa đỉnh i và đỉnh j


Ví dụ


u đi m và nh c đi mƯ ể ượ ể

Ưu điểm của ma trận liền kề:

Đơn giản, trực quan, dễ cài đặt trên máy tính

Để kiểm tra xem hai đỉnh (u, v) của đồ thị có kề nhau
hay không, ta chỉ việc kiểm tra bằng một phép so
sánh: a
uv
≠ 0.

Nhược điểm của ma trận liền kề:

Tiêu tốn bộ nhớ: bất kể số cạnh của đồ thị là nhiều
hay ít, ma trận liền kề luôn luôn đòi hỏi n
2

ô nhớ để lưu
các phần tử ma trận.

Khó làm việc với đồ thị có số lượng đỉnh lớn.


2. Danh sách c nhạ

Trong trường hợp đồ thị có n đỉnh, m cạnh, ta có thể biểu
diễn đồ thị dưới dạng danh sách cạnh, trong cách biểu diễn
này, người ta liệt kê tất cả các cạnh của đồ thị trong một danh
sách, mỗi phần tử của danh sách là một cặp (u, v) tương ứng
với một cạnh của đồ thị.

Danh sách được lưu trong bộ nhớ dưới dạng mảng hoặc
danh sách móc nối. Ví dụ với đồ thị dưới đây:



Ưu điểm của danh sách cạnh:

Trong trường hợp đồ thị có số cạnh tương đối nhỏ: chẳng
hạn m < 6n cách biểu diễn bằng danh sách cạnh sẽ tiết
kiệm được không gian lưu trữ, bởi nó chỉ cần 2m ô nhớ
để lưu danh sách cạnh.

Dể dàng duyệt tất cả các cạnh của đồ thị.
Nhược điểm của danh sách cạnh:

Nhược điểm cơ bản của danh sách cạnh là khi ta cần

duyệt tất cả các đỉnh kề với đỉnh v nào đó của đồ thị, thì
chẳng có cách nào khác là phải duyệt tất cả các cạnh, lọc
ra những cạnh có chứa đỉnh v và xét đỉnh còn lại.


3. Danh sách kề

Trong cách biểu diễn này, với mỗi đỉnh v của đồ thị, ta cho
tương ứng với nó một danh sách các đỉnh kề với v.
Đỉnh Đỉnh kề
1 2,3,5
2 1,3
3 1,2,4
4 3,5
5 1,4
Ưu điểm

Dễ dàng duyệt tất cả các đỉnh kề với một
đỉnh v cho trước

Dễ dàng duyệt tất cả các cạnh
Nhược điểm: Cài đặt danh sách kề có phần
dài dòng hơn.


III. Tính liên thông

Đường đi độ dài n từ đỉnh u đến đỉnh v trong đồ thị là một
dãy các cạnh e
1

, e
2
, e
n
với (u,x
1
) = e
1
; (x
1
,x
2
) = e
2
; (x
n-1
,v) =
e
n

Độ dài đường đi bằng với số cạnh mà nó đi qua

Chu trình là đường đi mà nó bắt đầu và kết thúc tại cùng
một đỉnh

Chu trình (đường đi) gọi là đơn khi nó không đi qua cùng
1 cạnh quá một lần

Một đồ thị được gọi là liên thông nếu có đường đi giữa
mọi cặp đỉnh phân biệt của đồ thị


Định lý: Giữa mọi cặp đỉnh của một đồ thị vô hướng
liên thông luôn có đường đi đơn



Một đồ thị không liên thông là hợp của 1 hay nhiều đồ thị con
liên thông. Các đồ thị này được gọi là các thành phần liên
thông

Đồ thị có hướng gọi là liên thông mạnh nếu có đường đi từ a
tới b và từ b tới a với a, b là hai đỉnh bất kỳ của đồ thị.


IV. Chu trình và đ ng đi Eulerườ

Bài toán bảy cây cầu Euler, còn gọi là Bảy cầu ở Königsberg
nảy sinh từ vấn đề cụ thể. Thành phố Königsberg, Đức (nay
là Kaliningrad, Nga) nằm trên sông Pregel, bao gồm hai hòn
đảo lớn nối với nhau và với đất liền bởi bảy cây cầu. Câu hỏi
đặt ra là có thể đi theo một tuyến đường mà đi qua mỗi cây
cầu đúng một lần rồi quay lại điểm xuất phát hay không. Năm
1736, Leonhard Euler đã chứng minh rằng điều đó là không
thể được. Trong lịch sử toán học, lời giải của Euler cho bài
toán bảy cây cầu ở Königsberg được coi là định lý đầu tiên
của lý thuyết đồ thị.

Các đ nh nghĩaị

Đường đi Euler (Eulerian path, Eulerian trail hoặc Euler
walk) trong đồ thị vô hướng là đường đi của đồ thị đi qua
tất cả các cạnh của đồ thị mỗi cạnh đúng một lần.

Chu trình Euler (Eulerian cycle, Eulerian circuit hoặc
Euler tour) trong đồ thị vô hướng là một chu trình đi qua
tất cả các cạnh của đồ thị mỗi cạnh đúng một lần.

Đồ thị gọi là đồ thị Euler khi nó chứa chu trình Euler và
được gọi là nửa Euler khi nó chứa đường đi Euler.


Đ nh lý Euler v chu trình và đ ng đi Eulerị ề ườ

Đối với các đồ thị có hướng, các thuật ngữ đường đi và
chu trình được thay bằng đường đi có hướng và chu
trình có hướng.

Đồ thị vô hướng liên thông G=(V, E) có chu trình Euler
khi và chỉ khi G không có đỉnh nào bậc lẻ.

Đồ thị vô hướng liên thông G=(V, E) có đường đi Euler
khi và chỉ khi G có không quá hai đỉnh bậc lẻ. Nếu G có
đúng hai đỉnh bậc lẻ thì đường đi Euler có hai đầu
đường đi nằm ở hai đỉnh bậc lẻ.


Mô t gi i thu t xây d ng chu trình Eulerả ả ậ ự


Input: Cho G = (V,E) là đồ thị vô hướng, liên thông , tất
cả các đỉnh đều có bậc chẵn.

Output: Chu trình Euler

Giải thuật xây dựng chu trình Euler

Bước 1: Xây dựng một chu trình đơn. Xuất phát từ đỉnh
bất kỳ, chẳng hạn x
0
, vì bậc x
0
lớn hơn 1, nên chọn được
cạnh u
0
= (x
o
,x
1
). Đến lượt x
1
, vì x
1
có bậc lớn hơn 1, nên
chọn được cạnh u
1
= (x
1
,x

2
) khác với u
0
. Tiếp tục như vậy,
vì số đỉnh là hữu hạn nên sau một số hữu hạn bước ta
gặp lại x
0
. Khi đó ta có một chu trình đơn, kí hiệu là C.



Nếu tất cả các cạnh của G đã nằm trong C thì C là chu
trình Euler của G.

Bước 2: Nếu còn cạnh của G chưa nằm trong C thì loại
các cạnh trong C và sau đó loại các đỉnh cô lập khỏi G,
gọi phần còn lại của G là G' . Khi đó G' vẫn là liên thông
và không có đỉnh bậc lẻ. Thêm nữa, vì G là liên thông
nên có ít nhất một đỉnh chung của C với G' .

Bước 3: Xuất phát từ đỉnh chung của G' và C, xây dựng
chu trình đơn C' của G' như trong bước 1, ghép C' vào
C và quay về bước 2.