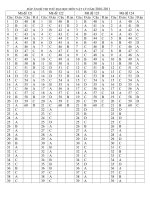
Đề-ĐA thi thu ĐH lan 3 THPT Tam Duong VP

SỞ GD − ĐT VĨNH PHÚC
TRƯỜNG THPT TAM DƯƠNG
  
ĐỀ KHẢO SÁT CHUYÊN ĐỀ NĂM HỌC 2009 − 2010
MÔN: TOÁN 12 KHỐI A, B LẦN 3
Thời gian làm bài: 180 phút
PHẦN I. DÀNH CHO TẤT CẢ CÁC THÍ SINH
Câu 1 (2.0 điểm). Cho hàm số
3 2
2
x
y
x
+
=
+
(C)
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2. Đường thẳng y = x cắt (C) tại hai điểm M, N. Tìm m để đường thẳng: y = x + m cắt (C) tại P, Q sao
cho tứ giác MNPQ là hình bình hành.
Câu 2 (2.0 điểm ).
1. Giải phương trình:
2 2
2sin 2sin tan
4
x x x
π
 
− = −
 ÷
 

.
2. Giải phương trình:
2 2
4 2 3 4x x x x+ − = + −
Câu 3 (1.0 điểm). Tính tích phân:
( )
4
3
0
ln 2 1
2 1
x
I dx
x
+
=
+
∫

Câu 4 (1.0 điểm).
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A;
0
60ABC∠ =
, AB = 2a. Cạnh
bên AA’ = 3a. Gọi M là trung điểm B’C’. Tính thể tích tứ diện A’BMC và khoảng cách từ C đến mặt
phẳng (A’BM)
Câu 5 (1.0 điểm).
Cho a, b, c > 0 thoả mãn abc = 1. Chứng minh rằng:
3
a b b c c a

a b c
c a b
+ + +
+ + ≥ + + +
PHẦN II. HỌC SINH LÀM THEO KHỐI THI
A. Dành cho học sinh thi khối A.
Câu 6a (2.0 điểm).
1. Giải bất phương trình:
( )
2 2 2
2 2 4
log log 3 5 log 3x x x− − ≥ −
.
2. Trong mặt phẳng với hệ tọa độ Đềcác vuông góc Oxy, cho tam giác ABC có đỉnh B(2; −1); đường
cao và đường phân giác trong qua hai đỉnh A, C lần lượt là: 3x − 4y + 27 = 0 và x + 2y − 5 = 0. Lập
phương trình các cạnh của tam giác ABC.
Câu 7a (1.0 điểm). Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x + 2y − z + 2 = 0, và
đường thẳng d:
1 2 1
2 3 1
x y z− + +
= =
. Viết phương trình tham số đường thẳng ∆ đi qua A(−1; −2; 3) cắt
đường thẳng d và song song với mặt phẳng (P).
B. Dành cho học sinh thi khối B.
Câu 6 Vb (2.0 điểm).
1. Giải bất phương trình
( ) ( )
2 2
1 5 3 1

3 5
log log 1 log log 1x x x x+ + > + −
.
2. Trong mặt phẳng với hệ tọa độ Đềcác vuông góc Oxy, cho tam giác ABC cân tại C. Biết đường cao
BH: 2x − 3y − 10 = 0 và cạnh AB: 5x + y − 8 = 0 và đỉnh A(1; 3). Xác định tọa độ các đỉnh B, C.
Câu 7b. (1.0 điểm). Trong không gian với hệ tọa độ Đềcác Oxyz, cho mặt phẳng (P): x − y − z − 1 = 0 và
đường thẳng d:
1 1 2
2 1 3
x y z+ − −
= =
. Viết phương trình chính tắc của đường thẳng ∆ đi qua A(1; 1; −2),
song song với mặt phẳng (P) và vuông góc với đường thẳng d.
−−−−−−−−−−−−−HẾT−−−−−−−−−−−−−
Cán bộ coi thi không giải thích gì thêm!
Họ và tên thí sinh: SBD:
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM TOÁN 12 KHỐI A, B
Câu Nội dung Điểm
Câu1
1. + TXĐ: R\{−2}
+ Sự biến thiên:
Giới hạn và tiệm cận:
3 2
lim lim 3
2
x x
x
y
x
→±∞ →±∞

+
= =
+
⇒ x = 3 là tiệm cận ngang.
2 2
3 2
lim lim
2
x x
x
y
x
± ±
→− →−
+
= = ±∞
+
⇒ x = −2 là tiệm cận đứng.
2
4
' 0
( 2)
y
x
= >
+
⇒ Hàm số đồng biến trên TXĐ
0.5
BBT 0.25
Đồ thị: 0.25

2. Đường thẳng y = x cắt đồ thị (C) tại hai điểm M(−1; −1) và N(2; 2) ⇒ MN
2
= 18
0.25
Hoành độ giao điểm của đường thẳng y = x + m và đồ thị (C) là nghiệm của PT:
2
3 2
( 1) 2 2 0
2
x
x m x m x m
x
+
= + ⇔ + − + − =
+
(*)
Điều kiện để y = x + m cắt (C) tại hai điểm phân biệt P, Q khác M, N là:
( ;5 4 2) (5 4 2; )m∈ −∞ − ∪ + +∞
0.25
Giả sử hoành độ của P và Q là x
1
, x
2
.( x
1
; x
2
là nghiệm của phương trình (*)
MNPQ là một hình bình hành khi và chỉ khi MN
2

= PQ
2
⇔
5 41m = ±
Cách 2: Do tính chất đỗi xứng nên I là tâm đối xứng của đồ thị cũng là tâm đối
xứng của hbh MNPQ.
Do đó khoảng cách từ I đến MN bằng khoảng cách từ I đến PQ.
0.5
Câu 2
1/. Điều kiện:
cos 0x
≠
(*)
2 2 2
sin
2sin 2sin tan 1 cos 2 2sin
4 2 cos
x
x x x x x
x
π π
   
− = − ⇔ − − = −
 ÷  ÷
   
0.5
( )
2
cos sin 2 .cos 2sin .cos sin cos sin sin 2 cos sin 0x x x x x x x x x x x
⇔ − − + ⇔ + − + =

sin cos tan 1
4
4 2
sin 2 1 2 2
2 4
x x x x k
x k
x x l x l
π

= − ⇒ = − ⇔ = − + π

π π
⇔ ⇒ = +

π π

= ⇔ = + π ⇔ = + π


0.5
2/.

Đk: −2 ≤ x ≤ 2.
Đặt
2
2 2 2 2
4
4 4 2 4 4
2

t
t x x t x x x x
−
= + − ⇒ = + − ⇒ − =
Phương trình có dạng
2
2
3 2 8 0
4
3
t
t t
t
=


− − = ⇔

= −

0.5
Với t = 2, ta có:
2
0
4 2
2
x
x x
x
=


− = − ⇔

=

Với
4
3
t = −
, phương trình vô nghiệm.
0.5
Câu 3
Đặt
2
2 1 2 1t x t x tdt dx= + ⇒ = + ⇒ =
0.25
Hướng dẫn chấm Toán 12 khối A, B Trang 2 /3
Với x = 0 ⇒ t =1; x = 4 ⇒ t = 3
Tích phân có dạng:
3
2
1
lnt
dt
t
∫
. 0.25
Đặt
2
1

ln
1
1
u t
du dt
t
dv dt
v
t
t

=

=

 
⇒
 
=
 
= −



. Vậy
3
2
1
3
1 1 1

ln (2 ln3)
1
3
I t dt
t
t
= − + = −
∫
0.5
Câu 4
Ta có:
2 3 , 4 , ' 2AC a BC a A M a= = =
Gọi A'H là đường cao của tam giác vuông A'B'C' ⇒ AH ⊥ (BCC'B') và
3AH a=
60
0
M
I
H
B'
A'
C'
C
B
A
0.25
Diện tích tam giác MBC là S
MBC
= 6a
2

.
Thể tích khối chóp A'MBC là
3
'
2 3
A MBC
V a=
0.25
Gọi B'I là đường cao của ∆ đều A'B'M ⇒
' 3, 2 3B I a BI a= =
và BI ⊥ A'M.
Diện tích ∆A'BM là
2
'
2 3
A BM
S a=
.
0.25
Do đó thể tích khối chóp C'ABM là:
3
. ' '
1
( ,( ' )). 2 3 ( ,( ' )) 3
3
C A MB A BM
V d C A BM S a d C A BM a= = ⇒ =
0.25
Câu 5
Áp dụng BĐT Côsi và Bunhiacopxki:

3 3a b c a b c+ + ≥ =
0.25
( )
2
a b c
a b c
a b c
c a b c a b
+ +
+ + ≥ = + +
+ +
0.25
( )
2
b c a
b c a
a b c
c a b c a b
+ +
+ + ≥ = + +
+ +

Cộng vế với vế ba BĐT trên ta có ĐPCM.
0.5
Câu
6a
1/. ĐK:
2 2
2 2
0

log log 3 0
x
x x
>



− − ≥


0.25
Đặt t = log
2
x,
BPT ⇔
2
2 3 5( 3) ( 3)( 1) 5( 3)t t t t t t− − > − ⇔ − + > −
0.25
2
2
2
1
log 1
1
3
3 4 3 log 4
( 1)( 3) 5( 3)
t
x
t

t
t x
t t t
≤ −

≤ −
≤ −



>

⇔ ⇔ ⇔




< < < <




+ − > −



0.25
Hướng dẫn chấm Toán 12 khối A, B Trang 3 /3





<<
≤<
⇔
168
2
1
0
x
x
Vậy BPT đã cho có tập nghiệm là:
1
0; (8;16)
2
 
∪


 
0.25
Câu
6a
2/. Phương trình cạnh BC là: 4x + 3y − 5 = 0
Tọa độ C là nghiệm của hệ phương trình
4 3 5 0 1
( 1;3)
2 5 0 3
x y x
C

x y y
+ − = = −
 
⇔ ⇒ −
 
+ − = =
 
0.25
Gọi B' là điểm đối xứng với B qua đường phân giác CD.
Phương trình BB' là:2x − y − 5 = 0
Giao điểm I của BB' và CD là nghiệm của hệ phương trình
2 5 0 3
(3;1) '(4;3)
2 5 0 1
x y x
I B
x y y
− − = =
 
⇔ ⇒ ⇒
 
+ − = =
 
0.25
PT cạnh AC (hay cạnh BB') là: y = 3.
Tọa độ A là nghiệm của hệ phương trình
3 4 27 0 5
( 5;3)
3 3
x y x

A
y y
− + = = −
 
⇔ ⇒ −
 
= =
 
0.25
Phương trình cạnh AB là: 4x + 7y − 1 = 0.
Ta có A, B nằm về cùng một phia đối với đường phân giác trong góc C ⇒ không
tồn tại tam giác
0.25
Câu
7a
Mp (P) có VTPT là
(2;2; 1)n = −
r
.
Đường thẳng d có phương trình tham số là:
1 2
2 3
1
x t
y t
z t
= +


= − +



= − +

.
Giả sử B(1 + 2t; −2 + 3t; −1 + t)∈d
0.25
Ta có:
(2 2;3 ; 4)AB t t t= + −
uuur
Đường thẳng ∆ cần tìm đi qua A, B và song song với mặt phẳng (P) khi và chỉ khi
8
. 0 2(2 2) 6 4 0 9 8
9
AB n t t t t t= ⇔ + + − + = ⇔ = − ⇔ = −
uuur r
0.25
2 8 44
; ;
9 3 9
AB
 
⇒ = − − −
 ÷
 
uuur
. Ta có thể chọn VTCP của ∆ là
(1;12;22)u =
r
0.25

Vậy phương trình tham số của ∆ là:
1 '
2 12 '
3 22 '
x t
y t
z t
= − +


= − +


= +

0.25
Câu
6b
1/. ĐK: x> 0
( )
( ) ( )
( ) ( ) ( )
2 2
3 1 3 5
5
2 2 2 2
3 1 5 5
5
1 log log 1 log log 1 0
log log 1 .log 1 0 log 1 1

x x x x
x x x x x x
⇔ + − + + + <
 
 ÷
⇔ + − + + < ⇔ + + <
 ÷
 
0.5
( )
2
5
0 log 1 1x x
⇔ < + + <
*)
( )
2
5
0 log 1 0x x x
< + + ⇔ >
0.5
Hướng dẫn chấm Toán 12 khối A, B Trang 4 /3
*)
( )
2 2 2
5
12
log 1 1 1 5 1 5
5
x x x x x x x

+ + < ⇔ + + < ⇔ + < − ⇔ <
Vậy BPT có nghiệm
12
0;
5
x
 
∈
 ÷
 
2/. Tọa độ B là nghiệm của HPT:
5 8 0 2
(2; 2)
2 3 10 0 2
x y x
B
x y y
+ − = =
 
⇔ ⇒ −
 
− − = = −
 
PT đường thẳng AC là: 3x + 2y − 9 = 0. Đường thẳng AB là: 5x + y − 8 = 0
0.5
Gọi I là trung điểm AB ⇒
3 1
;
2 2
I

 
 ÷
 
.
Phương trình đường cao CI là: x − 5y + 1 = 0.
Tọa độ C là nghiệm của HPT:
3 2 9 0
43 12
;
5 1 0
17 17
x y
C
x y
+ − =

 
⇒

 ÷
− + =
 

0.5
Câu
7b
Mặt phẳng (P) có VTPT
(1; 1; 1)n = − −
r
, đường thẳng d có VTCP

(2;1;3)u =
r
Vì
/ /( )
, ( 2; 5;1)
d
d
P u n
u n u
d
u u
∆
∆
∆

∆ ⊥


 
⇒ ⇒ = = − −
 
 
∆ ⊥
⊥



r r
r r r
r r

0.5
Đường thẳng ∆ đi qua A(1; 1; −2) có phương trình chính tắc là:
1 1 2
2 5 1
x y z− − +
= =
−
0.5
Hướng dẫn chấm Toán 12 khối A, B Trang 5 /3