Bài giảng lý thuyết điều khiển tự động - Phân tích và thiết kế hệ thống điều khiển rời rạc part 2 doc

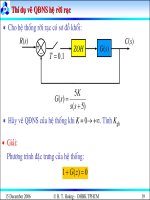
15 December 2006 â H. T. Hong - éHBK TPHCM 10
Th
Th
ớ
ớ
du
du
ù
ù
xe
xe
ự
ự
t o
t o
ồ
ồ
n
n
ủ
ủ
ũnh du
ũnh du
ứ
ứ
ng tieõu chua
ng tieõu chua
ồ
ồ
n Routh
n Routh

Hurwitz mụ
Hurwitz mụ
ỷ
ỷ
ro
ro
ọ
ọ
ng
ng






=

s
sHsG
zzGH
)()(
)1()(
1
Z
))()(1(
)(
)1(3

5.015.03
21
ìì


+
=
ezezz
BAzz
zz
)(
)1()1(
)(
)1()1(
))()(1(
)(
))((
1
abab
ebeeae
B
abab
eaeb
A
ezezz
BAzz
bsass
aTbTbTaT
bTaT
bTaT

=


=

+
=






++



Z






++
=

)1)(3(
3
)1(
1
sss
e
z
s
Z
)1(
1
)(
)3(
3
)(
+
=
+
=

s
sH
s
e
sG
s
0346.0
)31(3
)1()1(3
0673.0

)31(3
)1(3)1(
5.035.05.05.03
5.05.03
=


=
=


=
ìì

ì
eeee
B
ee
A

)607.0)(223.0(
104.0202.0
)(
2

+
=
zzz
z
zGH

15 December 2006 â H. T. Hong - éHBK TPHCM 11
Th
Th
ớ
ớ
du
du
ù
ù
xe
xe
ự
ự
t o
t o
ồ
ồ
n
n
ủ
ủ
ũnh du
ũnh du
ứ
ứ
ng tieõu chua
ng tieõu chua
ồ
ồ
n Routh

n Routh


Hurwitz mụ
Hurwitz mụ
ỷ
ỷ
ro
ro
ọ
ọ
ng
ng
Phửụng trỡnh ủaởc trửng:
0)(1 =+
z
G
H
)607.0)(223.0(
104.0202.0
)(
2

+
=
zzz
z
zGH

0104.0202.0135.083.0

234
=
+
+
+

z
z
z
z
0
)607.0)(223.0(
104.0202.0
1
2
=

+
+
zzz
z

ẹoồi bieỏn:
1
1

+
=
w
w

z
0104.0
1
1
202.0
1
1
135.0
1
1
83.0
1
1
234
=+







+
+

+
+







+








+
w
w
w
w
w
w
w
w

0597.1378.5624.679.1611.0

234
=
+
+
+
+ wwww

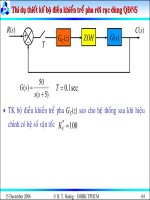
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 12
Th
Th
í
í
du
du
ï
ï
xe
xe
ù
ù
t o
t o
å
å
n
n
đ
đ
ònh du
ònh du

ø
ø
ng tiêu chua
ng tiêu chua
å
å
n Routh
n Routh
–
–
Hurwitz mơ
Hurwitz mơ
û
û
ro
ro
ä
ä
ng
ng
 Bảng Routh
0597.1378.5624.679.1611.0
234
=
+
+
+
+
wwww
 Kết luận: Hệ thống ổn đònh do tất cả các hệ số ở cột 1 của

bảng Routh đều dương
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 13
Tiêu chua
Tiêu chua
å
å
n Jury
n Jury
 Xét tính ổn đònh của hệ rời rạc có PTĐT:
0
1
1
10
=++++
−
−
nn
nn
azazaza L
 Tiêu chuẩn Jury: Điều kiện cần và đủ để hệ thống rời rạc ổn đònh
là tất cả các hệ số ở hàng lẻ, cột 1 của bảng Jury đều dương.
 Bảng Jury: gồm có (2n+1) hàng.
 Hàng 1 là các hệ số của PTĐT theo thứ tự chỉ số tăng dần.
 Hàng chẳn (bất kỳ) gồm các hệ số của hàng lẻ trước đó viết
theo thứ tự ngược lại.
 Hàng lẽ thứ i = 2k+1 (k≥1) gồm có (n
−
k+1) phần tử, phần tử
ở hàng i cột j xác đònh bởi công thức:
3,11,1

3,21,2
1,2
1
+−−−−
+−−−−
−
=
kjnii
kjnii
i
ij
cc
cc
c
c
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 14
Th
Th
í
í
du
du
ï
ï
xe
xe
ù
ù
t o
t o

å
å
n
n
đ
đ
ònh du
ònh du
ø
ø
ng tiêu chua
ng tiêu chua
å
å
n Jury
n Jury
 Do các hệ số ở hàng lẻ cột 1 bảng Jury đều dương nên hệ thống
ổn đònh.
01325
23
=
+
+
+
z
z
z
 Xét tính ổn đònh của hệ rời rạc có PTĐT là:
 Bảng Jury
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 15

Ph
Ph
ư
ư
ơng pha
ơng pha
ù
ù
p quỹ
p quỹ
đ
đ
a
a
ï
ï
o nghie
o nghie
ä
ä
m so
m so
á
á
(Q
(Q
Đ
Đ
NS)
NS)

 Quỹ đạo nghiệm số là tập hợp tất cả các nghiệm của phương
trình đặc trưng của hệ thống khi có một thông số nào đó trong hệ
thay đổi từ 0 →∞.
 Xét hệ rời rạc có phương trình đặc trưng:
0
)(
)(
1 =+
zD
zN
K
 Các qui tắc vẽ QĐNS hệ liên tục có thể áp dụng để vẽ QĐNS
của hệ rời rạc, chỉ khác qui tắc 8.
)(
)(
)(
0
zD
zN
KzG =
Đặt:
Gọi n và m là số cực và số zero của G
0
(z)
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 16
Ph
Ph
ư
ư
ơng pha

ơng pha
ù
ù
p quỹ
p quỹ
đ
đ
a
a
ï
ï
o nghie
o nghie
ä
ä
m so
m so
á
á
(Q
(Q
Đ
Đ
NS)
NS)
Qui ta
Qui ta
é
é
c vẽ Q

c vẽ Q
Đ
Đ
NS
NS
 Qui tắc 1: Số nhánh của quỹ đạo nghiệm số = bậc của phương
trình đặc tính = số cực của G
0
(z) = n.
 Qui tắc 2:
 Khi K = 0: các nhánh của quỹ đạo nghiệm số xuất phát từ các
cực của G
0
(z).
 Khi K tiến đến +∞ : m nhánh của quỹ đạo nghiệm số tiến đến
m zero của G
0
(z), n−m nhánh còn lại tiến đến ∞ theo các tiệm
cận xác đònh bởi qui tắc 5 và qui tắc 6.
 Qui tắc 3: Quỹ đạo nghiệm số đối xứng qua trục thực.
 Qui tắc 4: Một điểm trên trục thực thuộc về quỹ đạo nghiệm số
nếu tổng số cực và zero của G
0
(z) bên phải nó là một số lẻ.
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 17
Ph
Ph
ư
ư
ơng pha

ơng pha
ù
ù
p quỹ
p quỹ
đ
đ
a
a
ï
ï
o nghie
o nghie
ä
ä
m so
m so
á
á
(Q
(Q
Đ
Đ
NS)
NS)
Qui ta
Qui ta
é
é
c vẽ Q

c vẽ Q
Đ
Đ
NS (tt)
NS (tt)
 Qui tắc 7: : Điểm tách nhập (nếu có) của quỹ đạo nghiệm số nằm
trên trục thực và là nghiệm của phương trình:
0=
dz
dK
 Qui tắc 6: : Giao điểm giữa các tiệm cận với trục thực là điểm A
có tọa độ xác đònh bởi:
mn
zp
mn
OA
m
i
i
n
i
i
−
−
=
−
−
=
∑∑
∑∑

== 11
zerocực
(p
i
và z
i
là các cực
và các zero của G
0
(z) )
 Qui tắc 5: : Góc tạo bởi các đường tiệm cận của quỹ đạo nghiệm
số với trục thực xác đònh bởi :
mn
l
−
+
=
π
α
)12(
),2,1,0( K
±
±
=
l
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 18
Ph
Ph
ư
ư

ơng pha
ơng pha
ù
ù
p quỹ
p quỹ
đ
đ
a
a
ï
ï
o nghie
o nghie
ä
ä
m so
m so
á
á
(Q
(Q
Đ
Đ
NS)
NS)
Qui ta
Qui ta
é
é

c vẽ Q
c vẽ Q
Đ
Đ
NS (tt)
NS (tt)
 Qui tắc 8: : Giao điểm của quỹ đạo nghiệm số với vòng tròn đơn
vò có thể xác đònh bằng cách áp dụng tiêu chuẩn Routh–Hurwitz
mở rộng hoặc thay z=a+jb (a
2
+b
2
=1) vào phương trình đặc trưng.
 Qui tắc 9: Góc xuất phát của quỹ đạo nghiệm số tại cực phức p
j
được xác đònh bởi:
∑∑
≠
==
−−−+=
n
ji
i
ij
m
i
ijj
ppzp
11
0

)arg()arg(180
θ
Dạng hình học của công thức trên là:
θ
j
= 180
0
+ (∑góc từ các zero đến cực p
j
)
− (∑góc từ các cực còn lại đến cực p
j
)