Bài giảng lý thuyết điều khiển tự động - Phân tích và thiết kế hệ thống điều khiển rời rạc part 3 pot

15 December 2006 © H. T. Hồng - ÐHBK TPHCM 19
Th
Th
í
í
du
du
ï
ï
vẽ Q
vẽ Q
Đ
Đ
NS he
NS he
ä
ä
rơ
rơ
ø
ø
i ra
i ra
ï
ï
c
c
 Giải:
Phương trình đặc trưng của hệ thống:
0)(1
=

+
z
G
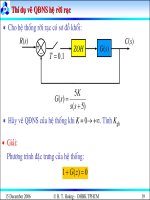
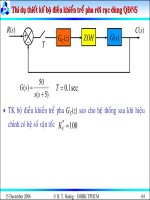
 Cho hệ thống rời rạc có sơ đồ khối:
)5(
5
)(
+
=
ss
K
sG
C(s)
+
−
G(s)
ZOH
R(s)
1.0
=
T
 Hãy vẽ QĐNS của hệ thống khi K = 0→ +∞. Tính K
gh
15 December 2006 â H. T. Hong - éHBK TPHCM 20
Th
Th
ớ
ớ
du
du

ù
ù
veừ Q
veừ Q
ẹ
ẹ
NS he
NS he
ọ
ọ
rụ
rụ
ứ
ứ
i ra
i ra
ù
ù
c
c






=

s
sG

zzG
)(
)1()(
1
Z
[
]
)()1(
)1()1(
)(
22 aT
aTaTaT
ezza
aTeezeaTz
ass
a



++
=






+
Z

+
=

)5(
5
)1(
2
1
ss
K
z
Z
)5(
5
)(
+
=
ss
K
sG

++
=



)()1(5
)]5.01()15.0[(
)1(
5.02
5.05.05.0
1
ezz
eezez
zK

)607.0)(1(
018.0021.0
)(

+
=
zz
z
KzG
Phửụng trỡnh ủaởc trửng:
0

)607.0)(1(
018.0021.0
1 =

+
+
zz
z
K
Cửùc:
1
1
=p 607.0
2
=
p
Zero:
857.0
1
=z
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 21
Th
Th
í
í
du
du
ï
ï
vẽ Q

vẽ Q
Đ
Đ
NS he
NS he
ä
ä
rơ
rơ
ø
ø
i ra
i ra
ï
ï
c
c
 Điểm tách nhập:
(PTĐT) ⇔
018.0021.0
607.0607.1
018.0021.0
)607.0)(1(
2
+
+−
−=
+
−−
−=

z
zz
z
zz
K
⇒
2
2
)018.0021.0(
042.0036.0021.0
+
−+
−=
z
zz
dz
dK
0=
dz
dK
Do đó
⇔



=
−=
792.0
506.2
2

1
z
z
 Tiệm cận:

12
)12()12(
−
+
=
−
+
=
π
π
α
l
mn
l
12
)857.0(]607.01[
zero
−
−
−
+
=
−
−
=

∑∑
mn
OA
cực
π
α
=
⇒
464.2
=
OA
⇒
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 22
Th
Th
í
í
du
du
ï
ï
vẽ Q
vẽ Q
Đ
Đ
NS he
NS he
ä
ä
rơ

rơ
ø
ø
i ra
i ra
ï
ï
c
c
 Giao điểm của QĐNS với vòng tròn đơn vò:
Cách 1: Dùng tiêu chuẩn Routh – Hurwitz mở rộng:
(PTĐT) ⇔
0)018.0021.0()607.0)(1(
=
+
+
−
−
z
K
z
z
(*)
0)607.0018.0()607.1021.0(
2
=++−+ KzKz
⇔
Đổi biến
1
1

−
+
=
w
w
z
, (*) trở thành:
0)607.0018.0(
1
1
)607.1021.0(
1
1
2
=++






−
+
−+







−
+
K
w
w
K
w
w
⇔
0)003.0214.3()036.0786.0(039.0
2
=−+−+ KwKKw
Theo hệ quả của tiêu chuẩn Hurwitz, điều kiện ổn đònh là:





>−
>−
>
0003.0214.3
0036.0786.0
0
K
K
K
⇒
83.21
=

gh
K





<
<
>
1071
83.21
0
K
K
K
⇔
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 23
Th
Th
í
í
du
du
ï
ï
vẽ Q
vẽ Q
Đ
Đ

NS he
NS he
ä
ä
rơ
rơ
ø
ø
i ra
i ra
ï
ï
c
c
Thay giá trò K
gh
= 21.83 vào phương trình (*), ta được:
011485.1
2
=
+
−
z
z
8187.05742.0 j
z
±
=
Vậy giao điểm của QĐNS với vòng tròn đơn vò là:
8187.05742.0 j

z
±
=
⇒
0)607.0018.0()607.1021.0(
2
=++−+ KzKz
Cách 2: Thay z = a + jb vào phương trình (*) :
0)607.0018.0())(607.1021.0()(
2
=+++−++ KjbaKjba
+−+−+−+ bKjaKbabja )607.1021.0()607.1021.0(2
22
0)607.0018.0(
=
+
K
⇒



=−+
=++−+−
0)607.1021.0(2
0)607.0018.0()607.1021.0(
22
bKjabj
KaKba
⇒
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 24

Th
Th
í
í
du
du
ï
ï
vẽ Q
vẽ Q
Đ
Đ
NS he
NS he
ä
ä
rơ
rơ
ø
ø
i ra
i ra
ï
ï
c
c
 Kết hợp với điều kiện a
2
+ b
2

=1, ta được hệ phương trình:





=+
=−+
=++−+−
1
0)607.1021.0(2
0)607.0018.0()607.1021.0(
22
22
ba
bKjabj
KaKba
khi
 Giải hệ phương trình trên, ta được 4 giao điểm là:
1−=
z
1071
=
K
khi
1=
z
0
=
K

8187.05742.0 j
z
±
=
khi
83.21
=
K
83.21
=
gh
K
⇒
15 December 2006 © H. T. Hoàng - ÐHBK TPHCM 25
Th
Th
í
í
du
du
ï
ï
veõ Q
veõ Q
Ñ
Ñ
NS he
NS he
ä
ä

rô
rô
ø
ø
i ra
i ra
ï
ï
c
c
0.607
−0.857
0
+1
−3
Im z
Re z
−1
+j
−
j
−2
−2.506 0.792
0.5742+j0.8187
0.5742−j0.8187
15 December 2006 © H. T. Hoàng - ÐHBK TPHCM 26
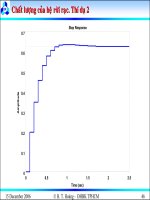
Cha
Cha
á
á

t l
t l
ö
ö
ô
ô
ï
ï
ng cu
ng cu
û
û
a he
a he
ä
ä
rô
rô
ø
ø
i ra
i ra
ï
ï
c
c
15 December 2006 © H. T. Hồng - ÐHBK TPHCM 27
Đ
Đ
a

a
ù
ù
p
p
ứ
ứ
ng cu
ng cu
û
û
a he
a he
ä
ä
rơ
rơ
ø
ø
i ra
i ra
ï
ï
c
c
 Đáp ứng của hệ rời rạc có thể tính bằng một trong hai cách sau:
 Cách 1: nếu hệ rời rạc mô tả bởi hàm truyền thì trước tiên ta
tính C(z), sau đó dùng phép biến đổi Z ngược để tìm c(k).
 Cách 2: nếu hệ rời rạc mô tả bởi PTTT thì trước tiên ta tính
nghiệm x(k) của PTTT, sau đó suy ra c(k).

 Cặp cực quyết đònh của hệ rời rạc là cặp cực nằm gần vòng tròn
đơn vò nhất.