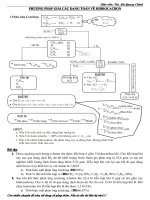
Phương pháp để làm loại toán tìm điều kiện tham số để hàm số đơn điệu trong khoảng
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (1.12 MB, 57 trang )
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
LỜI NÓI ĐẦU:
Tôiđãcốgắngrấtnhiềuđểcóthểtrìnhbày1cáchdễhiểunhất,giúpcácemcóthểnắm
bắtnộidungdễdàngnhất,nhưngvìkhôngcóthờigianvàtrìnhđộcòncóhạnnêntôi
viếthơidài,nếucóthờigiantôisẽviếtnóngắngọnhơn.
Tôihivọngđâylàchuyênđềbổíchchohọcsinh,đặcbiệtlàgiáoviên,chuyênđềnày
đãđigiảimãthànhcông1loạitoánquenthuộc,nócóthểápdụngchobấtkỳbàitoán
nàovềdạngchúngtađangbàntới.
Rấtmongnhậnđượcýkiếnđónggópcủacácđộcgiảvềphươngphápnày,cácđộcgiả
gửiýkiếnvềchotácgiảquađiachỉgmail:
Cuốicùngxinchânthànhcámơnđộcgiảđãđọcchuyênđềcủatôi,trongquátrìnhbiên
soạnsẽkhôngtránhkhỏisaisótnênmongđượcchỉgiáo.
TrầnMậuTú-TMT-
MỤC LỤC:
Cơsởlýluyếtvàtriểnkhaiýtưởng……………………………… 3->5.
Vídụvềsựđộcđáocủaphươngpháp………………………………5->49
Cácứngdụngđẹpvàhay……………………………………………49->HẾT.
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
CHUYÊNĐỀ:Biênsoạn:TrầnMậuTú-TMT-
Phong Thái Mới Cho
Loại Toán:
Tìm điều kiện để hàm số đơn điệu,
đạt cực trị trong 1 khoảng đoạn bất kỳ
nào đó
,
khoảng đoạn này tùy ý.
Vàcácứngdụngđẹp
ÔNTHINĂMNAY
Cácemthânmến,họctậpcần1niềmđammêvàsángtạo,cácemsẽthấyđược1
ứngdụngrấtđộcđáocủađịnhlýviète.
Loạitoánnàyrấtquenthuộc,nhưngcáchchúngtalàmloạitoánnàyvậndụng
phầnnhiềukiếnthứckhôngđượchọcởlớp,màkhiđithinếulàmcáccáchđóđôi
khicònkhôngcóđiểm,vàđặcbiệtcácemlạiphảinhớđịnhlýđảovềdấucủatam
thứcbậchai.
Chúngtasẽthấyđược1ứngdụngvôcùngđộcđáovềđịnhlýviete.
Đượctrìnhbàydướidạngtrìnhbàyvàowordnêncónhiềuvấnđềkhôngthểgiải
thíchcặnkẻđểcácemcóthểhiểuđượcsâu,bảnchấtcủavấnđề,nêntácgiảsẽ
thựchiện1videovềphươngphápnày,mongcácemủnghộnhiệttình.
Loạitoánnàycácemcóthểlàmtheocáchkhácnhau,nhưngphongcáchtrong
phươngphápnàyvôcùngthúvịvàấntượng,mongcácemcóthểthunhậnđược
kiếnthứctrongchuyênđềnày.
Trongquátrìnhbiênsoạnsẽkhôngtránhkhỏisaisót,mongcácemđónggópý
kiếnvàchỉgiáo
Tácgiả:TRẦNMẬUTÚ-TMT-
ThamgiachiasẽvàtraođổicùngGiaSưKhoaHọc:NickFB:
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
GiaSưBàiThiKhoaHọc:
/>
CƠSỞLÝTHUYẾTCHOPHƯƠNGPHÁPĐỐCĐÁOMÀANH
MUỐNGIỚITHIỆULÀĐÂY.
Chophươngtrìnhbậc2sau:
2
. 0 (a 0)a x bx c
có2nghiệm.
Khiđótacócácquanđiểmsau:
1. Phươngtrìnhcó2nghiệmtráidấunếu:
1 2
x . 0 0
c
x
a
2. Phươngtrìnhcó2cùngdấunếu:
1 2
x . 0 0
c
x
a
3. Phươngtrìnhcó2nghiệmâmnếu:
1 2
1 2
0
. 0
0
0
c
x x
a
x x b
a
4. Phươngtrìnhcó2nghiệmdươngnếu:
1 2
1 2
0
. 0
0
0
c
x x
a
x x b
a
Đó là các cơ sở lý thuyết để chúng ta đi đến các kết luận hết sức thú vị và có ứng
dụng vô cùng cao siêu như sau:
Xéthàmf(x)=
2
. (a 0)a x bx c
.
o f(x)có2nghiệmthỏamãn:
1 2 1 2
0x x x x
Cáchgiảiquyết:
Chúngtađặt:
t x x t
Khiđóbằngviệcthay
x t
vàof(x)tacó:
2
( ) (t ) (t ) (a 0 )f t a b c
là1hàmẩnlàt.
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
Dẫnđếnbàitoánrấtquenthuộclàf(t)=0có2nghiệmtráidấu:
1 2
0t t
.
Vàcáchgiảithìchúngtađãcóởtrênrồi,chúngtađãvậndụng1phépbiếnđổivôcùng
thúvị,tươngtựchocáchbiếnđổiđóchúngtacócácsảnphẩmtiếptheonhưsau:
o f(x)có2nghiệmthỏamãn:
1 2 1 2
0x x x x
Cáchgiảiquyết:
Chúngtađặt:
t x x t
Khiđóbằngviệcthay:
x t
vàof(x)tacó:
2
( ) (t ) (t ) (a 0 )f t a b c
là1hàmẩnlàt.
Khiđósẽdẫnđếnbàitoánvôcùngquyenthuộclàf(t)có2nghiệm
1 2
0t t
.
Cáchlàmloạinàychúngtađãnêuởtrêncủacơsởphươngpháp.
1 2
1 2
0
.t 0
0
0
c
t
a
t t b
a
o f(x)có2nghiệmthỏamãn:
1 2 1 2
0x x x x
Cáchgiảiquyết:
Chúngtađặt:
t x x t
Khiđóbằngviệcthay:
x t
vàof(x)tacó:
2
( ) (t ) (t ) (a 0 )f t a b c
là1hàmẩnlàt.
Khiđósẽdẫnđếnbàitoánvôcùngquyenthuộclàf(t)có2nghiệm
1 2
0t t
.
Cáchlàmloạinàychúngtađãnêuởtrêncủacơsởphươngpháp.
1 2
1 2
0
.t 0
0
0
c
t
a
t t b
a
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
Trênđólàcáccơsởcủaphươngphápchúngtasẽxoayquanhcácquanđiểmrấthữuích
màanhvừatriểnkhaiởtrên.
Facebook:GiaSưBaiThiKhoaHọc:
/>
CHÚNGTASẼTRẢIQUACÁCVÍDỤĐỂTHẤYĐƯỢCSỰĐỘC
ĐÁOCỦAPHƯƠNGPHÁPTRÊN.
Bài1:Chohàmsốsau:
3 2
3(2 1) (12 5) 1y x m x m x
Tìmcácgiátrịcủamđểhàmsốthỏamãncácđiềukiệnsau:
1. ĐồngbiếntrênR
2. Đồngbiếntrên
(1, )
.
3. Đòngbiếntrên
( , 3)
4. Đồngbiếntrên
( 1,2)
5. Nghịchbiếntrên
( 1,1)
.
6. Đồngbiếntrên
( , 1)
và
(2, )
7. Đồngbiếntrên
( 1,2)
và
(3,4)
.
8. Nghịchbiếntrên
( 1,0)
và
(1,2)
9. Nghịchbiếntrên
( 3,0)
và
(1,2)
10. Nghịchbiếntrênđoạncóđộdàibằng1.
Đâylàvídụrấtcơbảnnhất,vídụnàynhằmmụcđíchgiúpcácemlàmquenvớivới
phươngpháp,đồngthờianhsẽphântíchvàsosáchcáccáchlàmkhácvớiphươngpháp
anhđangbàntới.
Lờigiải:
Hàmsố:
3 2
2
2 2
'
2
'
3(2 1) (12 5) 1
' 0
3 6(2 1) 12 5 0
' 9(2 1) 3(12 5) 6(6 1)
' 6(6 1)
y
y
y x m x m x
y
x m x m
m m m
m
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
BBT:
Tathấyhàmsốluônphảiđồngbiếntrên(-∞,x
1
)và(x
2
,+∞)
Hàmsốnghịchbiếntròngkhoảng(x
1
,x
2
)
1.HàmsốđồngbiếntrênRkhivàchỉkhiy’
0vớimọixthuộcR.
2
'
2
3 6(2 1) 12 5 0
' 0
6(6 1) 0
1 1
6 6
y
x m x m
m
m
2.Hàmsốđồngbiếntrên
(1, )
khiy’
0vớimọi
(1, )x
.
x
y’
y
x
1
x
2
0
0
+
+
Y(
x
1
)
Y(
x
2
)
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
2
2
'
'
1 2
3 6(2 1) 12 5 0
' 6(6 1)
' 0
x (1, )
(1)
’ 2 : x 1(2)
y
y
y có nghiem thoa mãn x
x m x m
m
Cónhiềuemsẽhỏicái(2)làmthếnàomàcóđượcvậy,câutrảlờisẽđượctrìnhbày
trongvideocủaanh,vìrấtkhóđểviếtrathànhlờichocácemhiểuđượcsâubảnchất
củavấnđề,mongcácemđónxemvàthôngcảmvìchưacóthểgiảithíchchocácem
hiểusâubảnchấtcủacáchlàmnày.NhưngcácemnhìnvàoBBTsẽhiểuđượctạisaolại
cóđiềuđó,cácemnhìnxemtrênkhoảngnàothìh/sđồngbiến,nghịchbiếnsẽhiểuđược.
Facebook:GiaSưBàiThiKhoaHọc:
/>
Tađigiảiquyết(1):
'
2
' 0
6(6 )
1 0
1 1
6 6
y
m
m
Tađigiảiquyết(2):
1 2
’ 2 : x 1y có nghiem thoa mãn x
Cácemthânmến,chúngtasẽápdụngphươngpháptrênnhưsau:
1 2 1 2
1 2
x 1 x 1 1 0
1 1
0
x x
Đat t x x t
t t
Khiđótathayx=t+1vàoy’tađượchàmf(t):
2
2
2
2
'( )
' 3 6(2 1) 12 5
( ) 3( 1) 6(2 1)( 1) 12 5
3 12 2
' 36 6
f t
y x m x m
f t t m t m
t mt
m
Khiđóbàitoántrởthànhtìmmđểf(t)=0có2nghiệmâm
1 2
0t t
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
2
'( )
1 2
1 2
1
36 6 0
' 0
6
2 1
. 0 0
1
3
6
6
0
12
0
0
3
f t
m
m
t t m
m
t t
m
m
Từkếtquảcủa(1)và(2)chúngtađượcđiềukiệnbàitoánlà:
1 1
1
6 6
1
6
6
m
m
m
3. Hàmsốđồngbiếntrên
( , 3)
khiy’
0vớimọi
( , 3)x
2
2
'
'
2 1
3 6(2 1) 12 5 0
' 6(6 1)
' 0
x ( , 3)
(1)
’ 2 : 3x (2)
y
y
y có nghiem thoa mã
x m x m
n
m
x
Cáithứ(2)lấyđâuralàcả1tưduylogicrấttốtanhsẽbàntrongvideonhé,cácemnhớ
đónxem.
Tađigiảiquyết(1):
'
2
' 0
6(6 )
1 0
1 1
6 6
y
m
m
Tađigiảiquyết(2):
2 1
’ 2 x 3:y có nghiem th xoa mãn
Chúngtađiápdụngphươngphápnhưsau
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
2 2
2 1
1 1
x x
3 3 3 0
+3 3
0
Đat t x x t
x
t
x
t
Khiđótathayx=t-3vàoy’tađượchàmf(t):
2
2
2
2
2
'( )
2
' 3 6(2 1) 12 5
( ) 3( 3) 6(2 1)( 3) 12 5
3 12( 2) 48 50
( ) 3 12( 2) 48 50
' 36( 4 4 ) 3(48 50)
36 6
f t
y x m x m
f t t m t m
t m t m
f t t m t m
m m m
m
Khiđóbàitoántrởthànhtìmmđểf(t)=0có2nghiệmdương
2 1
0t t
2
'( )
1 2
1 2
1
6
36 6 0
1
1
' 0
48 50
66
. 0 0
50 1
3
50
0
4(m 2) 0
48
6
48
2
f t
m
m
mm
m
t t
m
m
t t
m
Từkếtquảcủa(1)và(2)tacókếtluậncủamlà:
1 1
6 6
1 50
48
6
50 1
48
6
m
m m
m
Lờibình:Cácemnhậnthấy,ýthứ2vàýthứ3chúngtađãlàm1phươngphápmàáp
dụngđinhlývieterấtđẹpmắt,cácemcóthểápdụngđểtìmmsaochohàmsốnghịch
biếntrêncáckhoảngdạng
( , ) ( ', )a hoac a
,hoàntoàntươngtựnhưvậy.Nhưng1điểm
lưuýlànếulàmnghịchbiếnthìyêucầuhệsốcủa
3
x
phảiâm.
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
Bâygiờchúngtasangý4vớikhoảngdạng(a,b).
4. Hàmsốđồngbiếntrên
( 1,2)
khiy’
0vớimọi
( 1,2) ( ,2) ( 1, )x
2
2
2 1
1 2
'
'
(1)
2
’ 2 : (2)
1.
3 6(2 1) 12 5 0 ( 1, 2) ( ,2) ( 1, )
' 6(6 1)
' 0
y
y
x
x x
y có nghiem thoa mãn
x
x m x m
m
x
Cáithứ(2)cóđượclànhờtưduylogic,rấtkhótrìnhbaychocácemhiểuđượckhiđánh
máyvìthếmờicácemxemvideođểhiểusâuvấnđềnhé.
Cácemvàonickfacebooksauđểhỏixemvideo:
GiaSưBàiThiKhoaHọc:
/>
Tatiếptụcgiảiquyếtbàitoántrên:
Tađigiảiquyết(1):
'
2
' 0
6(6 )
1 0
1 1
6 6
y
m
m
Tađigiảiquyết(2):
2 1
1 2
2
’ 2 :
1.
x x
y có nghiem thoa mãn
x x
Chúngtađilàmtrươnghợp:
2 1 2 1
2 2 2 0x x x x
.
Đặtt=x-2=>x=t+2thayvàoy’tađượchàmf(t)nhưsau:
2 1
0t t
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
2
2
2
2
2
'( )
2
' 3 6(2 1) 12 5
( ) 3( 2) 6(2 1)( 2) 12 5
3 6(1 2m) 12 5
( ) 3 6(1 2 ) 12 5
' 9(4 1 4 ) 3( 12 5)
36 6
f t
y x m x m
f t t m t m
t t m
f t t m t m
m m m
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmdương
2 1
0t t
2
'( )
1 2
1 2
1
6
36 6 0
' 0
1
5 12
. 0 0
6
3
0
5
2(2m 1)
0
12
1
2
f t
m
m
m
m
t t
t t
vô ngh em
m
m
i
Chúngtađilàmtrườnghợp:
1 2 1 2
1 1 1 0x x x x
.
Đặtt=x+1=>x=t-1thayvàoy’tađượchàmf(t)nhưsau:
1 2
0t t
2
2
2
2
2
'( )
2
' 3 6(2 1) 12 5
( ) 3( 1) 6(2 1)( 1) 12 5
3 12(1 m) 24 14
( ) 3 12(1 ) 24 14
' 36( 1 2 ) 3(24 14)
36 6
f t
y x m x m
f t t m t m
t t m
f t t m t m
m m m
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmâm
1 2
0t t
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
2
'( )
1 2
1 2
1
36 6 0
6
' 0
24 14
1
. 0 0 1
3
6
0
4(m 1) 0
7
12
1
f t
m
m
m
t t m
m
t t
m
m
Từkếtquảcủa(1)và(2)tacókếtluôncủamthoảnmãn:
1 1
6 6
1
m
m
5. Hàmsốnghịchbiếntrên
( 1,1)
khiy’
0vớimọi
( 1,1) ( ,1) ( 1, )x
1 2
2
2
1
'
1 2
2
3 6(2 1) 12 5 0 ( 1,1) ( , 1) (1, )
' 6(6 1)
1
’=0, 2 : 1 1
1
y
x
x x
y có nghiem thoa mãn x x
x m x m
m
x x
Cáitrêncóđượclànhờtưduylogic,rấtkhótrìnhbaychocácemhiểuđượckhiđánh
máyvìthếmờicácemxemvideođểhiểusâuvấnđềnhé.
Cácememvàonickfacebooksauđểhỏixemvideo:
GiaSưBàiThiKhoaHọc:
/>
Tatiếptụcgiảiquyếtbàitoántrên:
Tađigiảiquyếtvấnđề:
1 2
1 2
1 2
1
’=0, 2 : 1 1
1
x x
y có nghiem thoa mãn x x
x x
Đếnđâychúngtagiảiquyết2trườnghợptrênsauđógộplạiđểtìmm
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
Chúngtađilàmtrươnghợp:
1 2 1 2
1 1 0 1x x x x
.
Đặtt=x+1=>x=t-1thayvàoy’tađượchàmf(t)nhưsau:
1 2
0t t
2
2
2
2
2
'( )
2
' 3 6(2 1) 12 5
( ) 3( 1) 6(2 1)( 1) 12 5
3 12(1 m) 14
( ) 3 12(1 ) 24 14
' 36( 1 2 ) 3(24 14)
36 6
f t
y x m x m
f t t m t m
t t
f t t m t m
m m m
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmtráidấu:
1 2
0t t
1 2
24 14 7
. 0 0
3 12
m
t t m
(a)
Chúngtađilàmtrườnghợp:
1 2 1 2
1 1 0 1x x x x
.
Đặtt=x-1=>x=t+1thayvàoy’tađượchàmf(t)nhưsau:
1 2
0t t
2
2
2
2
'( )
' 3 6(2 1) 12 5
( ) 3( 1) 6(2 1)( 1) 12 5
3 12 2
' 36 6
f t
y x m x m
f t t m t m
t mt
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmtráidấu:
1 2
0t t
1 2
12 5 5
m
12
. 0 0
3
m
t t
(b)
Từ(a)và(b)tacókếtluậnvềgiátrịcủamlà:
5
m
7 5
12
7
12 12
12
m
m
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
Lờibình:Quaýthứ4vàthứ5,cácemđãcó1cáinhìnmớimẻvềphongcáchlàmloại
toánnàyrồichứquađótheocáchlàmtươngtựcácemcóthểtựlàmcácbàitậpkhác
hoàntoàntươngtự.Tiếptheotasangápdụngcholoạitoáncó2khoảngtrong1bài
toán.
6.Hàmsốđồngbiếntrong
( , 1)
và
(2, )
Khi
' 0y
vớimọi
, 1 (2, )x
2
3 6(2 1) 12 5 0, , 1 (2, )
x m x m x
Chúngtasẽđitìmmđểhàmsốđồngbiếntrêntừngkhoảngsauđógộpkếtquảlạisẽ
đượcđápáncủabàitoán.
Tasẽđitìmmđểhàmsốđồngbiếntrên
( , 1)
2
'
2 1
3 6(2 1) 12 5 0,
2 :
1
1
,
' 0
y
Có nghiem thoa mãn x x
x m x m x
Ta có:
'
2
' 0
6(6 )
1 0
1 1
6 6
y
m
m
(a)
Ta có:
2 1 2 1
2 : 1 1 1 0Có nghiem thoa mãn x x x x
Đặtt=x+1=>x=t-1,thayx=t-1vàoy’tađươchàmf(t)
2
2
2
2
2
'( )
2
' 3 6(2 1) 12 5
( ) 3( 1) 6(2 1)( 1) 12 5
3 12(1 m) 14
( ) 3 12(1 ) 24 14
' 36( 1 2 ) 3(24 14)
36 6
f t
y x m x m
f t t m t m
t t
f t t m t m
m m m
m
Khiđóđiềukiệnlà:f(t)=0có2nghiệmdương
2 1
0t t
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
2
'( )
1 2
1 2
1
36 6 0
7 1
6
' 0
12
24 14
6
1
. 0 0
1
3
6
0
4(m 1) 0
6
7
12
1
f t
m
m
m
m
t t
m
m
t t
m
m
(b)
Từ(a)và(b)tacóđiềukiệnđểhàmsốđồngbiếntrên
( , 1)
7 1
12
6
1 7
12
6
1 1
6 6
m
m m
m
(1)
Tasẽđitìmmđểhàmsốđồngbiếntrênkhoảng
(2, )
2
'
1 2
3 6(2 1) 12 5 0, 2,
'
2 2
0
:
y
x m x m
Có nghiem thoa mã x
x
n x
Ta có:
'
2
' 0
6(6 )
1 0
1 1
6 6
y
m
m
(c)
Ta có:
1 2 1 2
2 : 2 2 2 0Có nghiem thoa mãn x x x x
Đặtt=x-2=>x=t+2thayvàoy’tađượchàmf(t)nhưsau:
1 2
0t t
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
2
2
2
2
2
'( )
2
' 3 6(2 1) 12 5
( ) 3( 2) 6(2 1)( 2) 12 5
3 6(1 2m) 12 5
( ) 3 6(1 2 ) 12 5
' 9(4 1 4 ) 3( 12 5)
36 6
f t
y x m x m
f t t m t m
t t m
f t t m t m
m m m
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmâm
1 2
0t t
2
'( )
1 2
1 2
1
6
36 6 0
1
' 0
1
5 12
6
. 0 0
6
1 5
3
0
5
2(2m 1) 0
12
6
12
1
2
f t
m
m
m
m
m
t t
m
t t
m
m
(d)
Từ(c)và(d)tacóđiềukiệnđểhàmsốđồngbiếntrên
(2, )
1
6
1 5 5
12 12
6
1 1
6 6
m
m m
m
(2)
Từ(1)và(2)tacókếtluậncủabàitoánnhưsau:
Đểhàmsốđồngbiếntrênkhoảng
( , 1) 2, ( )va
:
7
7 5
12
5
12 12
12
m
m
m
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
7.Hàmsốđồngbiếntrênkhoảng
( 1,2)
và
(3,4)
Khi
' 0y
vớimọi
1,2 (3,4)x
2
3 6(2 1) 12 5 0, 1,2 (3,4)x m x m x
Chúngtasẽđitìmmđểhàmsốđồngbiếntrêntừngkhoảngsauđógộpkếtquảlạisẽ
đượcđápáncủabàitoán.
Tasẽđitìmmđểhàmsốđồngbiếntrên
( 1,2)
Dựavàoý4củabàitoánđãgiảiquyếtởtrêntacóngaykếtquảlà:
1 1
6 6
1
m
m
(1)
Tasẽditìmmđểhàmsốđồngbiếntrênkhoảng
(3, 4)
Hàmsốđồngbiếntrên
(3,7)
khiy’
0vớimọi
(3,7) ( ,4) (3, )x
2
2
2 1
1
'
2
'
( )
4
’ 2 : ( )
3
3 6(2 1) 12 5 0 (3,4) ( ,4) (3, )
' 6(6 1)
.
' 0
y
y
x
a
x x
y có nghiem thoa mãn b
x
x m x m
x
m
Cáithứ(b)cóđượclànhờtưduylogic,rấtkhótrìnhbaychocácemhiểuđượckhiđánh
máyvìthếmờicácemxemvideođểhiểusâuvấnđềnhé.
Cácemvàonickfacebooksauđểhỏixemvideo:
GiaSưBàiThiKhoaHọc:
/>
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
Tatiếptụcgiảiquyếtbàitoántrên:
Tađigiảiquyết(a):
'
2
' 0
6(6 )
1 0
1 1
6 6
y
m
m
Tađigiảiquyết(b):
2 1
1 2
4
’ 2 :
3.
x x
y có nghiem thoa mãn
x x
o Chúngtađilàmtrươnghợp:
2 1 2 1
4 4 4 0x x x x
.
Đặtt=x-4=>x=t+4thayvàoy’tađượchàmf(t)nhưsau:
2 1
0t t
2
2
2
2
2
'( )
2
' 3 6(2 1) 12 5
( ) 3( 4) 6(2 1)( 4) 12 5
3 6(3 2m) 36 29
( ) 3 6(3 2 ) 36 29
' 9(4 9 12 ) 3( 36 29)
36 6
f t
y x m x m
f t t m t m
t t m
f t t m t m
m m m
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmdương
2 1
0t t
2
'( )
1 2
1 2
1
6
36 6 0
' 0
1
29 36
. 0 0
6
3
0
29
2(2 3) 0
36
3
2
f t
m
m
m
m
t t
t t
m
vô nghiem
m
m
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
o Chúngtađilàmtrườnghợp:
1 2 1 2
3 3 3 0x x x x
.
Đặtt=x-3=>x=t+3thayvàoy’tađượchàmf(t)nhưsau:
1 2
0t t
2
2
2
2
2
'( )
2
' 3 6(2 1) 12 5
( ) 3( 3) 6(2 1)( 3) 12 5
3 12(1 m) 24 14
( ) 3 12(1 ) 24 14
' 36( 1 2 ) 3( 24 14)
36 6
f t
y x m x m
f t t m t m
t t m
f t t m t m
m m m
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmâm
1 2
0t t
2
'( )
1 2
1 2
1
36 6 0
1
6
' 0
24 14
6
1
. 0 0 1
1 7
3
6
0
4(m 1) 0
12
6
7
12
1
f t
m
m
m
m
t t m
m
m
t t
m
m
Từkếtquảcủa(a)và(b)tacókếtluôncủamthoảnmãn:
1 1
6 6
1
6
1 7
12
6
m
m
m
(2)
Từ(1)và(2)Hàmsốđồngbiếntrênkhoảng
( 1,2)
và
(3,4)
khi:
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
1 1
6 6
1
1 1
1 1
6 6
6 6
1
6
1 7
12
6
m
m
m
m
m
m
8.Hàmsốnghịchbiếntrong
( 1,0)
và
(1,2)
Khi
' 0y
vớimọi
1,0 (1,2)x
2
3 6(2 1) 12 5 0, 1,0 (1,2)x m x m x
Chúngtasẽđitìmmđểhàmsốnghịchbiếntrêntừngkhoảngsauđógộpkếtquảlạisẽ
đượcđápáncủabàitoán.
Tasẽđitìmmđểhàmsốnghịchbiếntrên
( 1,0)
Hàmsốnghịchbiếntrên
( 1,0)
khiy’
0vớimọi
( 1,0) ( ,0) ( 1, )x
1 2
2
2
1
'
1 2
2
3 6(2 1) 12 5 0 ( 1,0) ( ,0) ( 1, )
' 6(6 1)
1
’=0, 2 : 1 0
0
y
x
x x
y có nghiem thoa mãn x x
x m x m
m
x x
Cáitrêncóđượclànhờtưduylogic,rấtkhótrìnhbaychocácemhiểuđượckhiđánh
máyvìthếmờicácemxemvideođểhiểusâuvấnđềnhé.
Cácememvàonickfacebooksauđểhỏixemvideo:
GiaSưBàiThiKhoaHọc:
/>
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
Tatiếptụcgiảiquyếtbàitoántrên:
Tađigiảiquyếtvấnđề:
1 2
1 2
1 2
1
’=0, 2 : 1 0
0
x x
y có nghiem thoa mãn x x
x x
Đếnđâychúngtagiảiquyết2trườnghợptrênsauđógộplạiđểtìmm
o Chúngtađilàmtrươnghợp:
1 2 1 2
1 1 0 1x x x x
.
Đặtt=x+1=>x=t-1thayvàoy’tađượchàmf(t)nhưsau:
1 2
0t t
2
2
2
2
2
'( )
2
' 3 6(2 1) 12 5
( ) 3( 1) 6(2 1)( 1) 12 5
3 12(1 m) 14
( ) 3 12(1 ) 24 14
' 36( 1 2 ) 3(24 14)
36 6
f t
y x m x m
f t t m t m
t t
f t t m t m
m m m
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmtráidấu:
1 2
0t t
1 2
24 14 7
. 0 0
3 12
m
t t m
(a)
o Chúngtađilàmtrườnghợp
1 2
0x x
.
y’có2nghiệmtráidấu:
2
1 2
' 3 6(2 1) 12 5 0
. 0
12 5
0
3
5
12
2 :Có nghiemy x m x m
x x
trái d
m
a
m
u
(b)
Từ(a)và(b)tacókếtluậnvềgiátrịcủamlà:
5
m
7 5
12
7
12 12
12
m
m
(1)
Tasẽđitìmmđểhàmsốnghịchbiếntrên
(1,2)
Hàmsốnghịchbiếntrên
(1,2)
khiy’
0vớimọi
(1, 2) ( ,2) (1, )x
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
1 2
2
2
1
'
1 2
2
3 6(2 1) 12 5 0 (1,2) ( ,2) (1, )
' 6(6 1)
1
’=0, 2 : 1 2
2
y
x
x x
y có nghiem thoa m
x m x
ãn x
m
x
m
x
x
Cáitrêncóđượclànhờtưduylogic,rấtkhótrìnhbaychocácemhiểuđượckhiđánh
máyvìthếmờicácemxemvideođểhiểusâuvấnđềnhé.
Cácememvàonickfacebooksauđểhỏixemvideo:
GiaSưBàiThiKhoaHọc:
/>
Tatiếptụcgiảiquyếtbàitoántrên:
Tađigiảiquyếtvấnđề:
1 2
1 2
1 2
1
’=0, 2 : 1 2
2
x x
y có nghiem thoa mãn x x
x x
Đếnđâychúngtagiảiquyết2trườnghợptrênsauđógộplạiđểtìmm
o Chúngtađilàmtrươnghợp:
1 2 1 2
1 1 0 1x x x x
.
Đặtt=x-1=>x=t+1thayvàoy’tađượchàmf(t)nhưsau:
1 2
0t t
2
2
2
2
'( )
' 3 6(2 1) 12 5
( ) 3( 1) 6(2 1)( 1) 12 5
3 12 2
' 36 6
f t
y x m x m
f t t m t m
t mt
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmtráidấu:
1 2
0t t
1 2
12 5 5
. 0 0
3 12
m
t t m
(c)
o Chúngtađilàmtrườnghợp
1 2 1 2
2 2 0 2x x x x
..
Đặtt=x-2=>x=t+2thayvàoy’tađượchàmf(t)nhưsau:
1 2
0t t
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
2
2
2
2
2
'( )
2
' 3 6(2 1) 12 5
( ) 3( 2) 6(2 1)( 2) 12 5
3 6(1 2m) 12 5
( ) 3 6(1 2 ) 12 5
' 9(4 1 4 ) 3( 12 5)
36 6
f t
y x m x m
f t t m t m
t t m
f t t m t m
m m m
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmtráidấu:
1 2
0t t
1 2
5 12 5
. 0 0
3 12
m
t t m
(d)
Từ(c) và(d) tacóđiềukiệncủamlà:
5 5
12 12
m
(2)
Từ(1)và(2)tacókếtluậncủabàitoánlà:
5 5
12
7 5
5
12 12
12
12
m
m
m
9.Hàmsốnghịchbiếntrên
( 3,0)
và
(1,2)
Đểhàmsốnghịchbiếntrên
( 3,1) (0,2 )và
thìtacóđiềukiệnsau:
' 0y
vớimọixthuộc
( 3,0) , 2)(1
2
' 3 6(2 1) 12 5 0y x m x m
vớimọixthuộc
( 3,0) , 2)(1
Chúngtasẽđitìmmđểhàmsốnghịchbiếntrêntừngkhoảngsauđógộpkếtquảlạisẽ
đượcđápáncủabàitoán.
Tasẽđitìmmđểhàmsốnghịchbiếntrên
( 3,0)
Hàmsốnghịchbiếntrên
( 3,0)
khiy’
0vớimọi
( 3,0) ( ,0) ( 3, )x
1 2
2
2
1
'
1 2
2
3 6(2 1) 12 5 0 ( 3,0) ( ,0) ( 3, )
' 6(6 1)
3
’=0, 2 : 3 0
0
y
x
x x
y có nghiem thoa mãn x x
x m x m
m
x x
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
Cáitrêncóđượclànhờtưduylogic,rấtkhótrìnhbaychocácemhiểuđượckhiđánh
máyvìthếmờicácemxemvideođểhiểusâuvấnđềnhé.
Cácememvàonickfacebooksauđểhỏixemvideo:
GiaSưBàiThiKhoaHọc:
/>
Tatiếptụcgiảiquyếtbàitoántrên:
Tađigiảiquyếtvấnđề:
1 2
1 2
1 2
3
’=0, 2 : 3 0
0
x x
y có nghiem thoa mãn x x
x x
Đếnđâychúngtagiảiquyết2trườnghợptrênsauđógộplạiđểtìmm
o Chúngtađilàmtrươnghợp:
1 2 1 2
3 3 0 3x x x x
.
Đặtt=x+3=>x=t-3thayvàoy’tađượchàmf(t)nhưsau:
1 2
0t t
Khiđótathayx=t-3vàoy’tađượchàmf(t):
2
2
2
2
2
'( )
2
' 3 6(2 1) 12 5
( ) 3( 3) 6(2 1)( 3) 12 5
3 12( 2) 48 50
( ) 3 12( 2) 48 50
' 36( 4 4 ) 3(48 50)
36 6
f t
y x m x m
f t t m t m
t m t m
f t t m t m
m m m
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmtráidấu:
1 2
0t t
1 2
48 50 50
. 0 0
3 48
m
t t m
(a)
o Chúngtađilàmtrườnghợp
1 2
0x x
.
y’có2nghiệmtráidấu:
CLB Gia Sư Bài Thi Khoa Học:
…………………………………………………………… Trần Mậu Tú-TMT-……………………………………………………………………
TÔILÀNGƯỜIVIẾTCHUYÊNĐỀNÀYNHẰMGIÚPCÁCEMTƯDUY,PHÂNTÍCHCHỨKHÔNG
PHẢILÀGIÚPCÁCEM”TRÌNHBÀY1BÀITOÁN”VIỆCCỦACÁCEMLÀTỰMÌNHTRÌNHBÀY
DỰAVÀOÝTƯỞNGĐÓCỦATÔI.
TRẦNMẬUTÚ-TMT-
2
1 2
' 3 6(2 1) 12 5 0
. 0
12 5
0
3
5
12
2 :Có nghiemy x m x m
x x
trái d
m
a
m
u
(b)
Từ(a)và(b)tacókếtluậnvềgiátrịcủamlà:
50 5
48 12
m
(1)
Tasẽđitìmmđểhàmsốnghịchbiếntrên
(1,2)
Hàmsốnghịchbiếntrên
(1,2)
khiy’
0vớimọi
(1, 2) ( ,2) (1, )x
1 2
2
2
1
'
1 2
2
3 6(2 1) 12 5 0 (1,2) ( ,2) (1, )
' 6(6 1)
1
’=0, 2 : 1 2
2
y
x
x x
y có nghiem thoa m
x m x
ãn x
m
x
m
x
x
Cáitrêncóđượclànhờtưduylogic,rấtkhótrìnhbaychocácemhiểuđượckhiđánh
máyvìthếmờicácemxemvideođểhiểusâuvấnđềnhé.
Tatiếptụcgiảiquyếtbàitoántrên:
Tađigiảiquyếtvấnđề:
1 2
1 2
1 2
1
’=0, 2 : 1 2
2
x x
y có nghiem thoa mãn x x
x x
Đếnđâychúngtagiảiquyết2trườnghợptrênsauđógộplạiđểtìmm
o Chúngtađilàmtrươnghợp:
1 2 1 2
1 1 0 1x x x x
.
Đặtt=x-1=>x=t+1thayvàoy’tađượchàmf(t)nhưsau:
1 2
0t t
2
2
2
2
'( )
' 3 6(2 1) 12 5
( ) 3( 1) 6(2 1)( 1) 12 5
3 12 2
' 36 6
f t
y x m x m
f t t m t m
t mt
m
Khiđótacóđiềukiệntrởthành:f(t)có2nghiệmtráidấu:
1 2
0t t