CHUYÊN ĐỀ ÔN TẬP HÌNH HỌC 9

CHUYÊN ĐỀ HÌNH HỌC
CHUYÊN ĐỀ 1:
1. Đường trung bình của tam giác, của hình thang.
2. Đường trung tuyến của tam giác vuông.
Ví dụ 1: Cho tam giác ABC đều, đường cao AD, trực tâm H. M là điểm bất kỳ
trên cạnh BC. Gọi E, F thứ tự là hình chiếu của M trên AB và AC. Gọi I là trung
điểm của AM. ID cắt EF tại K.
a) DEIF là hình gì?
b) CM: M, K, H thẳng hàng.
c) Xác định vị trí của M trên BC để EF đạt GTNN.
d) Tìm GTNN của S
DEIF
biết tam giác ABC có cạnh bằng a.
Lời giải:
Giã sử M nằm giữa B và D:
a)
∆
IED có:
·
·
0
1
2
2. 60
IE ID AM
EID BAD

= =




= =


⇒ ∆
IED là tam giác đều (1)
Chứng minh tương tự ta được
∆
IFD là tam giác đều (2). Từ
(1) và (2) suy ra DEIF là hình
thoi.
b) Vì
∆
ABC đều nên trực tâm
H củng là trọng tâm. Suy ra:
AH = 2.HD
Gọi P là trung điểm của AH
⇒
AP = PH = HD. Suy ra IP,
KH thứ tự là đường trung bình
của các tam giác AMH và DIP
⇒
MH // IP và KH // IP, suy ra M, K, H thẳng hàng.
c) Vì
∆
EDK vuông tại K nên ta có: EF = 2.EK = 2. ED.
·
sinKDE
=
3
.DE Do đó

EF đạt GTNN
⇔
DE đạt GTNN
⇔
DE
⊥
AB
⇔
M trùng với D.
( Có thể dùng định lý pitago để tính EF theo DE ).
d) S
DEIF
=
1
.EF
2
DI
Ví dụ 2: Cho tứ giác ABCD. Gọi A
/
, B
/
, C
/
, D
/
lần lượt là trọng tâm của các tam
giác BCD, ACD, ABD, ABC. CMR: AA
/
, BB
/

, CC
/
, DD
/
đồng qui.
Hoàng Kim Đỉnh THCS Chùa Hang 1
P
K
H
I
F
E
M
D
C
A
B
CHUYÊN ĐỀ HÌNH HỌC
Lời giải:
Gọi M, N, I lần lượt là
trung điểm của BD, AC và
A
/
C. Ta có:
+) NI là đường trung bình
của
∆
AA
/
C

⇒
AA
/
// NI.
+)
∆
MNI có A
/
là trung
điểm của MI và
AA
/
// NI
⇒
K là trung
điểm của MN.
Chứng minh tương tự thì
BB
/
, CC
/
, DD
/
đều đi qua
trung điểm K của MN
⇒
AA
/
, BB
/

, CC
/
, DD
/
đồng qui tại K.
Bài tập:
BT.1: CMR: Trọng tâm, trực tâm và tâm đường tròn ngoại tiếp của một tam giác
cùng nằm trên một đường thẳng.
BT.2: Cho đoạn thẳng AC và điểm B nằm giữa A và C. Vẽ các tam giác vuông
cân ABD và BCE trên cùng một nửa mặt phẳng bờ là AC. Gọi I là trung điểm
của AC. Tam giác IDE là tam giác gì? Vì sao?

CHUYÊN ĐỀ 2:
1. Định lí Talet và hệ quả
2. Tam giác đồng dạng
3. Hệ thức lượng trong tam giác vuông
* Những điểm lưu ý:
1- Định lý Talet và tam giác đồng dạng chỉ đề cập tới tỉ số của hai đối tượng cùng
loại ( cùng là độ dài, cùng là diện tích, …)
2- Đối với các bài toán cần thực hiện phép toán
A C
B D
±
ta thường dùng định lí
Talet hoặc tính chất của tam giác đồng dạng để biến đổi
/
/
;
A M C M
B N D N

= =
sao
cho N = N
/
. Trong hình học rất hiếm khi ta thực hiện phép nhân chéo
A C
B D
±
. .
.
A D B C
B D
±
=
.
Hoàng Kim Đỉnh THCS Chùa Hang 1
I
A
/
K
N
M
D
C
B
A
CHUYÊN ĐỀ HÌNH HỌC
3- Đối với bài toán cần thực hiện phép toán
.
A C

B D
ta thường biến đổi
A M
B N
=
,
/
/
C M
D N
=
trong đó N = M
/
.
4- Đối với bài toán cần chứng minh đẳng thức có dạng
1 1 1
A B C
± =
ta cần tìm các
đoạn thẳng M = N = P và chứng minh
M N P
A B C
± =
lúc này ta có thể dùng định lí
Talet hoặc tính chất của tam giác đồng dạng.
5- Đối với bài toán cần chứng minh đẳng thức dạng a.b = c.d + e.f ta thường
tách b = x +y và chứng minh a.x = c.d và b.y = e.f
6- Đối với bài toán cần chứng minh đẳng thức dạng a
2
= c.d + e.f làm tương tự

như trên.
Ví dụ 1: Cho D, E, F lần lượt nằm trên các cạnh BC, AC, AB của tam giác ABC
sao cho AD, BE, CF đồng
qui tại M. Chứng minh
rằng:
AF
BF
AM AE
DM CE
= +
.
* Định hướng: Cần chuyển
các tỉ số ở vế phải về cùng
mẫu.
Lời giải:
Qua A vẽ đường thẳng
song song với BC cắt BE
và CF tại I và K. Áp dụng
định lí Talet ta có:
AE AI
CE BC
=
và
AF AK
BF BC
=
AF
BF
AE KI
CE BC

⇒ + =
(1)
AM AI AK AI AK KI
DM BD CD BD CD BC
+
= = = =
+
(2). Từ (1) và (2) suy ra đpcm.
Ví dụ 2: Cho tam giác ABC. Một đường thẳng đi qua trọng tâm G của tam giác
cắt tia BC và các cạnh CA, AB tại D, E, F. CMR:

1 1 1
GD GE GF
+ =
.
Hoàng Kim Đỉnh THCS Chùa Hang 1
K
I
M
F
E
D
C
B
A
CHUYÊN ĐỀ HÌNH HỌC
Định hướng: ( xem lưu ý 4 )
Lời giải:
Vẽ CI // FE, BK // FE
⇒

CI = BK; MK = MI.
A.d định lí Talet ta có:
(1)
(2)
(3)
CI AI
GE AG
CI MI
GD MG
BK AK
GF AG

=



=



=


Cộng từng vế của (1) và
(2) sẽ được (3).
⇒
CI CI BK
GD GE GF
+ =
⇒

đpcm.
Ví dụ 3: Cho tam giác ABC. Biết rằng đường phân giác ngoài của góc A cắt BC
kéo dài tại E. CMR: AE
2
= EB. EC – AB. AC
Phân tích:
1.Cần tách AE = x – y
thỏa mãn: AE.x = EB. EC
và AE.y = AB. AC
2. Giã sử tồn tại M thuộc
EA để: EA. EM = EB. EC
⇐

EAC EBM∆ ∆ ⇐:
·
·
EMB ECA
=
.
Lời giải:
Lấy M thuộc tia đối của tia
AE sao cho
·
·
EMB ECA
=
.
⇒
EAC EBM∆ ∆:
suy ra

EA. EM = EB. EC (1).
Lại có:
EAC BAM∆ ∆:
⇒
EA. AM = AB. AC (2). Lấy (1) – (2) ta có đpcm.
Ví dụ 4: Cho 4 điểm theo thứ tự E, B, D, C cùng nằm trên một đường thẳng thỏa
mãn:
DB EB
DC EC
=
và A là một điểm sao cho AE
⊥
AD. CMR: AD và AE thứ tự là
phân giác trong và ngoài của tam giác ABC.
Hoàng Kim Đỉnh THCS Chùa Hang 1
K
I
M
G
F
E
D
C
B
A
X
M
E
C
B

A
CHUYÊN ĐỀ HÌNH HỌC
* Định hướng: - Chỉ cần chứng minh AD hoặc AE là phân giác
- Vẽ đường phụ là đt song song để sử dụng (gt)
DB EB
DC EC
=
.
N
M
E
D
C
B
A
Cách 1: Qua B vẽ đường thẳng song song với AC cắt AD và AE tại M và N.
Theo định lí Talet ta có:
DB BM
DC AC
BM BN
EB BN
EC AC

=


⇒ =


=



( Vì
DB EB
DC EC
=
).
Tam giác AMN vuông tại A có AB là trung tuyến
⇒
AB = MB. Suy ra
·
·
BAM BMA
=
(1). Lại có
·
·
CAM BMA
=
( vì BM // AC ) (2). Do đó AD là phân
giác trong của
∆
ABC
⇒
AE là phân giác ngoài ( vì AE
⊥
AD ).
Cách 2:
Qua C vẽ đt song song với AB cắt AD, AE tại M và N. Tương tự cách 1 ta cũng
chứng minh được:

·
·
BAM CMA
=
và
·
·
CAM CMA
=
.
Ví dụ 5: Cho hình thoi ABCD có
µ
0
60B =
. Một đường thẳng đi qua D không cắt
hình thoi nhưng cắt các đường thẳng AB, BC lần lượt tại E, F. Gọi M là giao
điểm của AF và CE. CMR:
a)
∆
EAC đồng dạng với
∆
ACF.
b) AD là tiếp tuyến của đường tròn ngoại tiếp
∆
MDF.
Lời giải:
a) Ta có
∆
EAD đồng dạng với
∆

DCF
AE CD
AD CF
⇒ =
AE AC
AC CF
⇒ =
(vì AD = AC
= CD ).
Xét
∆
EAC và
∆
ACF có:
·
·
0
120EAC ACF= =
và
AE AC
AC CF
=
; suy ra:
Hoàng Kim Đỉnh THCS Chùa Hang 1
CHUYÊN ĐỀ HÌNH HỌC
∆
EAC đồng dạng với
∆
ACF (c.g.c)
b) Chứng minh được

∆
ACM đồng dạng với
∆
AFC
2
.AFAC AM
⇒ =
mà AC = AD nên ta có
2
.AFAD AM
=
, suy ra AD
là tiếp tuyến của đường
tròn ngoại tiếp tam giác
MDF.
Ví dụ 6: Cho tam giác ABC vuông tại A, có
µ
0
20B =
. Kẻ phân giác BI. Vẽ góc
·
0
30ACH =
về phía trong tam giác. CMR: HI song song với phân giác của góc
HCB.
Lời giải:
Gọi CK là phân giác
của góc HCB.
Ta có:
AI BA

IC BC
=
(t.c
đường phân giác) (1).
Tam giác ACH
vuông tại A có
·
0
30ACH =
, suy ra:
2
CH
AH
=
. Khi đó vì
CK là phân giác của góc HCB nên ta có:
1
1
2
.
2
CH
AH CB
HK HK BK
= =
(2)
Kẻ
KM BC⊥
, vì tam giác KCB cân tại K nên: CB = 2BM (3). Từ (2) và (3)
đồng thời kết hợp với

∆
BMK đồng dạng với
∆
BAC suy ra:
Hoàng Kim Đỉnh THCS Chùa Hang 1
M
K
I
H
C
B
A
M
F
E
A
D
C
B
CHUYÊN ĐỀ HÌNH HỌC
AH BM BA
HK BK BC
= =
(4). Từ (1) và (4) suy ra điều phải chứng minh.
Bài tập:
BT.1) Cho tam giác ABC, AD là phân giác trong của góc A ( D
∈
BC ). CMR:
AD
2

= AB.AC – DB.DC
BT.2) Cho hình thang ABCD ( BC // AD ). Gọi M, N là hai điểm lần lượt trên
hai cạnh AB và CD sao cho
AM CN
AB CD
=
. Đường thẳng MN cắt AC và BD lần
lượt ở E và F. CMR: EM = FN
BT.3)Cho tam giác đều ABC. Gọi D là trung điểm cạnh BC và E, F là các điểm
thứ tự thuộc các cạnh AB, AC sao cho
·
0
60EDF
=
.
1. Chứng minh:
a)
∆
BDE đồng dạng với
∆
CFD.
b) BE. CF không đổi
c) ED
2
= EF. EB
d) EF luôn tiếp xúc với một đường tròn cố định.
2. Tìm vị trí của các điểm E, F để diện tích tam giác DEF đạt GTLN.
3. Tìm vị trí của các điểm E, F để diện tích tam giác AEF đạt GTLN.

CHUYÊN ĐỀ 3: TỨ GIÁC NỘI TIẾP

N
M
D
C
B
A
• Đối với tứ giác ABCD cho trước, các khẳng định sau là tương đương:
1. ABCD là tứ giác nội tiếp.
2.
µ
µ
µ
µ
0
A + C = B + D = 180
.
3.
·
·
ABC = ACD
.
4. MA.MC = MB. MD ( trong đó M là giao điểm của AC và BD ).
5. NA.NB = NC.ND ( trong đó N là giao điểm của AB và CD )
Hoàng Kim Đỉnh THCS Chùa Hang 1
CHUYÊN ĐỀ HÌNH HỌC
S
C
B
A
• Cho tam giác ABC và điểm S thuộc tia đối của tia BC.

Khi đó các khẳng định sau là tương đương.
1. SA là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
2.
·
·
ACB = BAS
.
3. SA
2
= SB.SC.
Ví dụ 1:Cho tam giác ABC vuông tại A, đường cao AH ( H
∈
BC ). Gọi I, J, K
lần lượt là tâm các đường tròn nội tiếp
∆
ABC,
∆
AHB và
∆
AHC. CMR:
a) AI
⊥
JK.
b) BJKC là tứ giác nội tiếp.
Lời giải:
a) Dễ thấy
ABHM là tứ
giác nội tiếp, suy
ra BM
⊥

AK.
Tương tự: CN
⊥
AJ. Vậy I là trực
tâm
∆
AJK, suy
ra đpcm.
b) Ta có:
·
µ
0
45
2
C
JBC
= −
.
·
¶
·
·
µ
0
IAJ 45
2
C
IKJ IAB JAB
= = − = −
( vì

·
·
µ
1 1
2 2
JAB HAB C
= =
).
Ví dụ 2: Cho đường tròn tâm O và S cố định nằm ngoài (O). Một cát tuyến thay
đổi đi qua S cắt (O) tại A và B ( A khác B ).
a) Đường thẳng d vuông góc với OS tại S và cắt các tiếp tuyến với (O) tại A và B
lần lượt ở C và D. Chứng minh: SC = SD.
b) Gọi E là giao điểm của các tiếp tuyến với đường tròn tại A và B. CMR: Khi
cát tuyến SAB thay đổi thì E luôn nằm trên một đường thẳng cố định; xác định
đường thẳng đó.
Hoàng Kim Đỉnh THCS Chùa Hang 1
N
M
K
J
I
H
C
B
A
CHUYÊN ĐỀ HÌNH HỌC
Lời giải:
a) Từ các tứ giác nội tiếp
SOBD và SAOC suy ra
·

·
SDO SCO
=
, từ đó suy ra SC
= SD.
b) Vẽ EI
⊥
SO. Dễ thấy SIKE
là tứ giác nội tiếp, suy ra: OI.
OS = OK. OE (1).
- Tam giác OBE vuông tại B
có đường cao là BK, suy ra:
OK. OE = OB
2
= R
2
(2). Từ
(1) và (2) suy ra:
2
OS
R
OI =
,
không đổi. Vậy E nằm trên
đường thẳng EI cố định ( chỉ
hai phần đt nằm ngoài đường
tròn ).
Ví dụ 3: Từ điểm K ở ngoài
đường tròn (O) vẽ hai tiếp
tuyến KA, KC và cát tuyến

KBD với đường tròn ( A, C là tiếp điểm; B nằm giữa K và D ). Gọi M là giao
điểm của OK và AC. CMR:
a) AB. CD = AD. BC
b) Tứ giác BMOD nội tiếp
c) Tứ giác BMOE nội tiếp ( E là
giao AC và đường thẳng qua O
vuông góc với BD ).
d) BE là tiếp tuyến của (O)
e) I, A, C thẳng hàng với I là giao
điểm các tiếp tuyến tại B và D.
f) AC luôn đi qua một điểm cố định
khi K thay đổi trên BD cố định ( K
ở ngoài (O)).

Lời giải:
a)
∆
KBA
:
∆
KAD
AB KB
AD KA
⇒ =
Hoàng Kim Đỉnh THCS Chùa Hang 1
K
I
C
D
O

E
B
A
S
E
M
O
D
B
C
A
K
CHUYÊN ĐỀ HÌNH HỌC
∆
KBC
:
∆
KCD
CB KB
CD KC
⇒ =
.Mà
KA = KC
⇒
AB CB
AD CD
=
⇒
đpcm
b) CM được KB. KD = KM. KO

c) Có
·
· ·
BMK BDO DBO= =
; suy ra:
·
·
BME BOE=
⇒
đpcm.
d) Suy ra từ (c)
e) Có
·
0
90AMO
=
. Lại có IBMOD
cùng nằm trên một đường tròn nên
suy ra
·
·
0
90IMO IBO
= =
⇒
đpcm.
f) Suy ra từ (e).
Ví dụ 4: Từ một điểm A ngoài đường tròn tâm O, vẽ các tiếp tuyến AD, AE ( D,
E là các tiếp điểm ). Tia AO cắt đường tròn tâm O tại B, C ( B ở giữa A và C ).
Kẻ DH vuông góc với CE tại H. Gọi P là trung điểm của DH. Tia CP cắt đường

tròn tâm O tại Q ( Q
≠
C ). Gọi giao điểm của AC và DE là I. CMR:
a) DQIP là tứ giác nội tiếp đường tròn.
b) AC là tiếp tuyến của đường tròn đi qua 3 điểm A, D, Q.
Lời giải:
a) Ta có:
·
·
DQP DIP
=
( =
·
DEC
).
b) Vì
·
0
90DPI =
⇒
·
0
90DQI
=
, suy ra:
·
·
QIA QDI
=
( cùng phụ với

·
QID
).
Hoàng Kim Đỉnh THCS Chùa Hang 1
I
M
O
D
B
C
A
K
H
P
Q
O
I
E
D
C
B
A
CHUYÊN ĐỀ HÌNH HỌC
Mặt khác
·
·
·
·
QEA QDI QIA QEA
= ⇒ =

nên tứ giác AQIE nội tiếp đường tròn. Suy
ra
· ·
·
QAI QEI ADQ
= =
⇒
đpcm.
Ví dụ 5: Cho tam giác ABC ( AB < AC ) có
·
0
60BAC
=
, đường phân giác trong
của góc
·
BAC
cắt BC tại D. Từ D kẻ các tia Dx // AC, Dy // AB cắt AB, AC thứ
tự tại M, N.
a) CMR: MN
2
= MB. NC
b) Đường tròn ngoại tiếp tam giác MND cắt BD tại E ( E khác D ). Gọi giao
điểm của BN với CM là F. Chứng minh MBEF là tứ giác nội tiếp.
c) Chứng minh tia EF đi qua trung điểm của MN.
Lời giải:
a) Dễ thấy AMDN là
hình thoi và MDN là
tam giác đều, suy ra:
MN

2
= MD. ND (1).
Mặt khác hai tam giác
BMD và DNC đồng
dạng với nhau, do đó:
MD. ND = MB. NC
(2). Từ (1) và (2) suy
ra đpcm.
b) Tứ giác MNDE nội
tiếp suy ra:
·
·
0
60MEB MND
= =
(1)
Từ (a) suy ra hai tam
giác BMN và MNC đồng dạng với nhau; suy ra:
·
·
·
·
·
MBN NMC MFB MNB NMC
= ⇒ = +
=
·
·
MNB MBN
+

=
·
0 0
180 60BMN
− =
(2).
Từ (1) và (2) suy ra đpcm.
c) Vì MBEF nội tiếp nên ta có
·
·
EFM MBF
=
·
·
EI IMF IMF IEMM
⇒ = ⇒ ∆ ∆
:
2
IF.IEMI
⇒ =
(1). Chứng minh tương tự thì NCEF là tứ giác nội tiếp và ta củng
chứng minh được: NI
2
= IF. IE (2). Từ đó suy ra IM = IN.
Ví dụ 6: Cho đường tròn (O) và đường thẳng d không cắt nó. Điểm M thay đổi
trên d, kẻ các tiếp tuyến MT, MH với (O) ( T, H là tiếp điểm ).
a) Chứng minh TH luôn đi qua một điểm cố định khi M chạy trên d.
b) Tìm quỹ tích của điểm N là giao điểm của OM và TH.
c) Gọi A là hình chiếu của O trên d và E, F, K thứ tự là hình chiếu của A trên
MT, MH, TH. CMR: E, F, K thẳng hàng.

d) CMR: EF luôn đi qua một điểm cố định khi M chạy trên d.
Hoàng Kim Đỉnh THCS Chùa Hang 1
I
E
F
N
M
D
C
B
A
CHUYÊN ĐỀ HÌNH HỌC
Bài tập:
1) Cho hình vuông ABCD. Trên cạnh BC lấy điểm M và trên CD lấy N sao cho
·
0
45MAN =
. Gọi I, K thứ tự là giao điểm của BD với AM và AN; P là giao
điểm của MK và NI.
a) Chứng minh AP
⊥
MN.
b) Tính tỉ số
KI
MN
.
c) Chứng tỏ MN luôn tiếp xúc với một đường tròn cố định.
2) Cho tam giác nhọn ABC có BC cố định,
µ
0

60A =
và nội tiếp (O;R) cho trước.
Gọi K là giao điểm của 3 đường phân giác trong của tam giác đó.
a) Chứng minh B, K, O, C cùng nằm trên một đường tròn, xác định tâm của
đường tròn này.
b) Xác định vị trí của A để ( KB + KC ) đạt GTLN.
3) Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai đường thẳng AD và
BC cắt nhau tại T. Vẽ đường thẳng d vuông góc với OT tại T.
a)Biết d cắt hai đường thẳng AC và BD theo thứ tự tại M và N. CMR: TM = TN.
b)Biết d cắt hai đường thẳng AB và CD theo thứ tự tại E và F. CMR: TE = TF.
4) Cho góc vuông xOy và tam giác ABC vuông tại A; trong đó A cố định nằm
trong góc xOy; B chạy trên Ox; C chạy trên Oy. Tìm quỹ tích hình chiếu vuông
góc của A trên BC.
CHUYÊN ĐỀ 4: KHAI THÁC BÀI TẬP HÌNH HỌC ( SKKN: 08 – 09 )
Hoàng Kim Đỉnh THCS Chùa Hang 1
⇔
R
D
C
O
B
A
M
R
D
C
O
B
E
A

M
O
D
M
C
B
A
CHUYÊN ĐỀ HÌNH HỌC
1) Khai thác bài toán dựa vào cấu trúc lôgic giữa các mệnh đề hình học:
Ví dụ 1: ( Bài 30 – SGK – Trang 116 )
Cho nửa đường tròn (O;R) đường kính AB. M
là điểm thuộc nửa đường tròn; tiếp tuyến của (O;R)
tại M cắt các tiếp tuyến tại A và B lần lượt ở C và D.
Chứng minh rằng:
a)
·
o
COD = 90
.
b) CD = AC + BD.
c) AC. BD = R
2
.
Đây là một bài toán rất quen thuộc có trong SGK – Toán 9 và hầu hết các em đều
giải được. Tuy nhiên rất ít HS thấy được sự tương đương giữa các khẳng định
sau:
(1) CD là tiếp tuyến.
(2)
·
90

o
COD
=
.
(3) CD = AC + BD.
(4) AC. BD = R
2
.
Thật vậy, kéo dài OD cắt AC tại E. Dễ dàng chứng
minh
được OD = OE , AE = BD (*).
+) Nếu
·
90
o
COD
=
thì từ (*) suy ra
∆
CED cân tại C
⇒
CO là phân giác của góc ECD
⇒
O cách CD một
khoảng bằng OA ( = R )
⇒
CD là tiếp tuyến của
(O;R).
+) Nếu CD = AC + BD thì từ (*) suy ra CD = CE
⇒

∆
CED cân tại C và cũng suy ra được CD là tiếp
tuyến của (O;R).
+) Nếu AC. BD = R
2
thì từ (*)
⇒
AC. AE = OA
2

⇒
ACO OCE
∆ ∆
:
(c.g.c)
·
·
0
90COE CAO
⇒ = =
⇒
∆
CED cân
tại C và cũng suy ra được CD là tiếp tuyến của (O;R).
Dựa vào sự tương đương giữa các kết quả trên
giáo viên có thể thiết kế thành nhiều bài toán khác nhau
để học sinh luyện tập.
Ví dụ 2: ( Bài 20 – SBT – Toán 9 ).
Cho tam giác đều ABC nội tiếp đường tròn (O)

và M là một điểm của cung nhỏ BC. Trên MA lấy
điểm D sao cho MD = MB.
a) Tam giác MBD là tam giác gì ?
b) So sánh hai tam giác BDA và BMC.
Hoàng Kim Đỉnh THCS Chùa Hang 1
D
O
M
C
B
A
CHUYÊN ĐỀ HÌNH HỌC
c) Chứng minh MA = MB + MC.
Đây là bài toán rất quen thuộc , lời giải có trong SBT và nhiều tài liệu
khác, kết quả cụ thể là:
a)
∆
MBD là tam giác đều.
b)
∆
BDA =
∆
BMC.
c) MA = MB + MC.
Nhận thấy rằng nếu xem:
+ ) Hình H là: “ Đường tròn ngoại tiếp tam giác đều ABC”.
+ ) Tính chất T là: “ Trong ba đoạn MA , MB , MC có một đoạn bằng tổng của
hai đoạn còn lại”.
Thì ta chứng minh được:
1) Mọi điểm thuộc hình H thì có tính chất T và ngược lại.

2) Những điểm không thuộc hình H thì không có tính chất T và ngược lại.
Do đó giáo viên có thể ra cho HS những bài tập sau:
Bài 1: Cho tam giác đều ABC nội tiếp đường tròn (O) và M là một điểm không
thuộc (O). Chứng minh rằng ba đoạn thẳng MA , MB , MC là độ dài ba cạnh của
một tam giác.
Gợi ý:
* Xét trường hợp điểm M nằm trong góc BAC ( các trường hợp khác hoàn toàn
tương tự ).
Vẽ tam giác đều BMD
⇒
MB = MD và
·
60
o
BMD
=
(1).
Dễ dàng chứng minh được
∆
BDA =
∆
BMC (c.g.c )
⇒
MC = DA (2).
Vì M
∉
(O) nên
·
60
o

BMA
≠
(3). Từ (1), (2) và (3) suy ra A, D , M không thẳng
hàng và MA , MB , MC là độ dài ba cạnh của tam giác MAD.
Bài 2: Cho tam giác đều ABC nội tiếp đường tròn (O) và M là một điểm thuộc
nửa mặt phẳng không chứa A bờ BC và thỏa mãn MA = MB + MC. Chứng minh
rằng ABMC là tứ giác nội tiếp.
Gợi ý: Làm tương tự bài toán 1 và chứng minh được MB = MD , MC = DA. Suy
ra MB + MC = MA = MD + DA
D MA
⇒ ∈
·
·
0
60BMA BMD
⇒ = =
·
·
BMA BC A
⇒ =
, suy
ra ABMC là tứ giác nội tiếp.
Bài toán 2 có thể diễn đạt dưới các bài tập sau:
Hoàng Kim Đỉnh THCS Chùa Hang 1
D
O
M
C
B
A

N
M
C
B
A
1
A
CHUYÊN ĐỀ HÌNH HỌC
Bài 3: Cho tam giác đều ABC cố định và một điểm M thuộc mặt phẳng (ABC)
sao cho trong 3 đoạn MA , MB , MC luôn tồn tại một đoạn bằng tổng của hai
đoạn kia. Chứng minh rằng điểm M chạy trên một đường tròn cố định.
Bài 4: Cho tam giác đều ABC cố định và một điểm M thuộc mặt phẳng (ABC).
Gọi x , y , z thứ tự là khoảng cách từ M tới A , B và C. Biết rằng trong ba số x ,
y , z luôn có một số bằng tổng của hai số còn lại. Tìm quỹ tích điểm M.
Gợi ý:
- Vận dụng bài toán 2 để tìm ra hình H là đường tròn ngoại tiếp tam giác
đều ABC.
- Vận dụng ví dụ 2 để chứng minh phần đảo.
Qua một số ví dụ ở trên ta thấy được nếu người dạy biết nắm bắt cấu trúc
lôgic của mỗi bài toán thì sẻ tạo ra được nhiều bài toán mới , hình thành cho học
sinh thói quen nhìn nhận một bài toán theo nhiều hướng khác nhau. Từ đó gúp
HS phát huy được năng lực giải toán.
Bây giờ ta lại tiếp cận ví dụ 2 theo hướng sau:
“Cho tam giác ABC nội tiếp đường tròn (O) và M là một điểm thuộc
cung BC ( không chứa A ). Các khẳng định sau có tương đương với nhau
hay không ?
(A): Tam giác ABC đều.
(B): MA = MB + MC.”
Trong trường hợp này nhiều HS vẫn ngộ nhận là từ (B)
cũng suy được ra (A). Điều này là không thể .

Thật vậy , xét tam giác đều BCA
1
ta có: MA
1
= MB +
MC ( theo vd.2 ).
Lấy A đối xứng với A
1
qua đường kính MN , suy ra A
thuộc (O) và MA = MA
1
( tính chất đối xứng ). Do đó với tam giác không đều
ABC ta vẫn có MA = MB + MC.
Để xây dựng bài toán ngược lại trong tình huống này
giáo viên cần bổ sung thêm điều kiện để ràng buộc điểm
A. Chẳng hạn ta phát biểu bài toán mới như sau:
Bài 5: Cho tam giác ABC cân tại A nội tiếp đường tròn
(O); M là một điểm thuộc cung BC không chứa A. Chứng
minh rằng nếu MA = MB + MC (*) thì ABC là tam giác
đều.
Gợi ý:
Vì tam giác ABC cân tại A nên MA là phân giác của góc
BMC. Do đó:
MB MA
MBI MAC
BI AC
∆ ∆ ⇒ =:
. .MB AC MA BI
⇒ =
(1).

MC MA
MCI MAB
CI AB
∆ ∆ ⇒ =:
. .MC AB MA CI
⇒ =
(2).
Vì AB = AC nên từ (1) và (2) suy ra:
Hoàng Kim Đỉnh THCS Chùa Hang 1
I
M
C
B
A
O
D
M
C
B
A
CHUYÊN ĐỀ HÌNH HỌC
( )
. .
BC
MA MB AB MA BC MA MB MA
AB
+ = ⇒ + =
. Kết hợp với (*) suy ra được
1
BC

AB BC
AB
= ⇒ = ⇒
đpcm.
2 ) Khai thác bài toán mới dựa trên kết quả của bài toán cũ:
Trong ví dụ 2 , nếu lấy kết quả “ MA = MB + MC ” làm tiền đề cho việc
khai thác các bài toán mới thì ta có các kết quả sau:
Bài 6: Cho tam giác đều ABC nội tiếp đường tròn (O) cố định; M là một điểm
thuộc cung nhỏ BC. Xác định vị trí của điểm M để:
a) Chu vi của tam giác MBC đạt giá trị lớn nhất.
b) Tổng ( MA + MB + MC ) đạt giá trị lớn nhất.
Gợi ý: a) Chu vi của
∆
MBC đạt giá trị lớn nhất
⇔
MB
+ MC lớn nhất
⇔
MA lớn nhất
⇔
MA là đường kính
⇔
M là trung điểm của cung nhỏ BC.
b) Làm tương tự.
Nếu kết hợp với BĐT – Cô si thì ta có ngay kết
quả: MA = MB + MB
2 .MB MC
≥
. Dấu bằng xảy ra khi
M nằm chính giữa cung nhỏ BC và khi đó MA cũng đạt

giá trị lớn nhất. Từ đó ta có bài toán sau:
Bài 7: Cho tam giác đều ABC nội tiếp đường tròn (O;R) cố định; M là một điểm
thuộc cung nhỏ BC. Tìm giá trị lớn nhất của (MA.MB.MC).
Nếu gọi E là giao điểm của MA và BC thì ta nhận thấy:
MB MA MB MC
BME AMC
ME MC MC
+
∆ ⇒ = =:
. Suy ra
1 1 1
.
MB MC
ME MB MC MB MC
+
= = +
. Từ đó ta có bài toán:
Bài 8: Cho tam giác đều ABC nội tiếp đường tròn (O);
M là một điểm thuộc cung nhỏ BC. Các đoạn thẳng
MA và BC cắt nhau tại E. Chứng minh rằng:
1 1 1
ME MB MC
= +
.
Khai thác kết quả bài toán 7, ta nhận ra rằng nếu
gọi F là trung điểm cung BC thì ta có
·
0
AF ,AMF 90BC⊥ =
.

Suy ra:
AF,AE AHAM
≤ ≥
.
Do vậy ME = AM – AE
≤
AF – AH = FH
1 1
ME F H
⇒ ≥
( không đổi ). Dấu bằng
xảy ra
M F
⇔ ≡
. Từ đó ta có được bài toán như sau:
Hoàng Kim Đỉnh THCS Chùa Hang 1
H
F
E
M
C
B
A
I
K
H
C
B
A
CHUYÊN ĐỀ HÌNH HỌC

Bài 9: Cho tam giác đều ABC nội tiếp đường tròn (O); M là một điểm thuộc
cung nhỏ BC. Các đoạn thẳng MA và BC cắt nhau tại E. Xác định vị trí của M
trên cung nhỏ BC để
1 1
MB MC
+
đạt giá trị nhỏ nhất.
Ta lại thấy rầng khi M trùng với F thì
1
MA
cũng đạt giá trị nhỏ nhất. Từ đó
ta lại có thêm bài toán hay và khó như sau:
Bài 10: Cho tam giác đều ABC nội tiếp đường tròn (O); M là một điểm thuộc
cung nhỏ BC. Các đoạn thẳng MA và BC cắt nhau tại E. Xác định vị trí của M
trên cung nhỏ BC để
1
MA
+
1 1
MB MC
+
đạt giá trị nhỏ nhất.
Ví dụ 3: Cho tam giác ABC vuông tại A. Gọi H là hình chiếu của A trên BC; I
và K thứ tự là trung điểm của AH và CK. Chứng minh:
⊥
BI AK
.
Gợi ý:
Ta có:
KH KC

IH IA
=

⇒

=

IK là đường trung bình của tam giác AHC suy ra
IK // AC
⇒
IK
⊥
AB. Do đó I là trực tâm của tam giác ABK,
suy ra BI
⊥
AK.
Từ kết quả của bài toán trên ta có nhận xét sau:
- Những đường thẳng song song với AK thì vuông
góc với BI.
- Những đường thẳng song song với BI
thì vuông góc với AK.
Từ đó ta tạo các bài toán mới như sau:
+ Gọi D là điểm đối xứng với C qua A
⇒
DH song
song với AK , từ kết quả của ví dụ 3 suy ra BI
⊥
DH. Từ đó ta có bài toán:
Bài 11: Cho tam giác BCD cân tại B; đường cao
BA. Gọi H là hình chiếu của A trên BC; I là trung

điểm của AH. Chứng minh rằng DH
⊥
BI.
+ Nếu tạo hình bình hành BDKI thì suy ra DK song song với BI do đó DK vuông
góc với AK. Từ đó ta có bài toán mới như sau:
Bài 12: Cho hình thang vuông ABDC (
0
90A B
∠ = ∠ =
) và BD =
1
2
AC. Gọi H là
hình chiếu của A trên BC, K là trung điểm của HC. Chứng minh rằng DK
⊥
AK.
Gợi ý:
Gọi I là trung điểm của AH.Theo ví dụ 3 ta có BI
⊥
AK(1)
Hoàng Kim Đỉnh THCS Chùa Hang 1
I
H
D
C
B
A
CHUYÊN ĐỀ HÌNH HỌC
Vì IK là đường trung bình của tam giác HAC nên suy ra được
1

2
IK AC BD
= =
.
Tứ giác BDKI có BD // KI và BD = KI
⇒
BDKI là hình
bình hành; suy ra DK // BI (2). Từ (1) và (2)
⇒
đpcm.
+ Nếu lấy E đối xứng với B qua D thì tứ giác ABEC là
hình chử nhật từ đó ta có bài toán sau:
Bài 13: Cho hình chữ nhật ABEC. Gọi H là hình chiếu
của A trên BC; D và K thứ tự là trung điểm của BE và
HC. Chứng minh rằng AK
⊥
DK.
( Giải tương tự bài 12 ).
Xem xét kỹ ví dụ 3 ta thấy kết quả bài toán không hề thay đổi khi ta thay
đường trung bình IK bằng đường thẳng song song với AC. Với cách tiếp cận
này thì ví dụ còn được khai thác theo hướng sau.
3) Chuyển từ quan hệ bằng nhau sang quan hệ đồng dạng để có bài toán
mới:
Với hướng này thì ví dụ 3 có thể diễn đạt như sau:
Bài 14: Cho tam giác ABC vuông tại A. Gọi H là hình chiếu
của A trên BC; I và K thứ tự là hai điểm thuộc AH và CK
sao cho
HK HI
KC IA
=

. Chứng minh:
BI AK
⊥
.
Gợi ý:
Vì
HK HI
KC IA
=
⇒
KI // AC ( Talet đảo ) mà AC
⊥
AB
⇒
KI
⊥
AB. Suy ra I là trực tâm của tam giác ABK
⇒
BI
⊥
AK.
Từ các bài toán 11 , 12 , 13 giúp ta có thêm các bài toán sau:
Bài 15: Cho tam giác nhọn BDC đường cao BA. Gọi H là
hình chiếu của A trên BC; I là một điểm thuộc đoạn AH sao cho
IH AD
IA AC
=
.
Chứng minh rằng DH
⊥

BI.
Gợi ý:
- Vẽ IK // AC
⇒
BI
⊥
AK (1).
- Chứng minh được DH // AK nhờ vào
định lý Talet đảo (2).
Hoàng Kim Đỉnh THCS Chùa Hang 1
K
D
I
H
C
B
A
I
K
H
B
C
A
K
I
H
A
C
B
D

CHUYÊN ĐỀ HÌNH HỌC
Bài 16: Cho hình thang vuông ABDC (
0
90A B
∠ = ∠ =
) và AC = m; BD = n. Gọi
H là hình chiếu của A trên BC, K thuộc đoạn HC sao cho
HK n
HC m
=
. Chứng minh
rằng DK
⊥
AK.
Gợi ý: Từ K vẽ KI // AC // BD
⇒
KI
⊥
AB; suy ra I là
trực tâm của tam giác ABK
⇒
BI
⊥
AK (1).
Vì IK // AC
⇒
IK
AC
=
HK n

HC m
=
BD
AC
=
⇒
IK = BD. Tứ
giác BDKI có BD = IK và BD // IK
⇒
BDKI là hình
bình hành
⇒
DK // BI (2). Từ (1) và (2)
⇒
DK
⊥
AK.
Bài 17: Cho hình chử nhật ABEC. Gọi H là hình
chiếu của A trên BC; Trên các
đoạn BE và HC lấy các điểm D và K sao cho
BD HK
BE HC
=
.
Chứng minh rằng AK
⊥
DK.
( Giải tương tự bài 16 ).
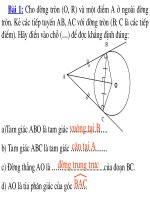
BÀI TẬP:
Cho tam giác ABC cố định có

·
·
ABC ACB
α
= =
. Gọi D là trung điểm cạnh BC;
đường tròn (O) tiếp xúc với AB , AC thứ tự tại I và K. E , F thứ tự là hai điểm
thay đổi trên AB và AC. Xét mối quan hệ giữa các khẳng định sau để tạo ra các
bài toán tương tự.
(a)
·
EDF
α
=
.
(b) EF là tiếp tuyến của đường tròn (D;DI).
(c) ED
2
= EF. EB.
(d) Chu vi của
∆
AEF bằng ( AI + AK ).
Hoàng Kim Đỉnh THCS Chùa Hang 1
n
m
I
K
H
D
C

B
A