600 CÂU TRẮC NGHIỆM TÍCH PHÂN VÀ ỨNG DỤNG ÔN THI THPT Quốc gia (File Word có đáp án)

NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : TÍCH PHÂN VÀ ỨNG DỤNG
ĐỀ SỐ 01
C©u 1 :

f ( x) =

x(2 + x)
( x + 1)2

Hàmsốnàodướiđâykhônglànguyênhàmcủahàmsố
A.

x2 − x − 1
x +1

B.

C©u 2 :

0

C.

∫

−3

0

1

f ( x)dx + ∫ f ( x)dx

B.

4

−3

4

0

0

∫ f ( x)dx + ∫ f ( x)dx

1

12

∫

−3

4

f ( x)dx + ∫ f ( x)dx
1

4

D.

Diệntíchhìnhphẳnggiớihạnbởicácđồthị:

C©u 4 :

D.

x2
x+1

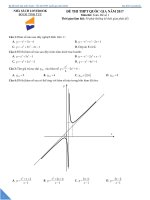
. Diệntíchhìnhphẳng (phầngạchtronghình) là:

C©u 3 :

A.

C.

x2 + x + 1
x+1

y = f ( x)

Cho đồthịhàmsố

A.

x2 + x − 1
x+1

B.

10
3

y = x2 − 2x

∫ f ( x)dx

−3

và

y = − x2 + x

C. 9

cókếtquảlà:
D. 6

Kếtquảnàosaitrongcáckếtquảsao?

A.

2 x + 1 − 5 x −1
1
2

∫ 10x dx = 5.2 x.ln 2 + 5x.ln 5 + C

B.

∫

C.

x2
1 x+1
∫ 1 − x2 dx = 2 ln x − 1 − x + C

D.

∫ tan

x 4 + x −4 + 2
1
dx = ln x − 4 + C
3
x
4x
2

xdx = tan x − x + C

1


C©u 5 :

1

x

y = x 2 .e 2 , x = 1 , x = 2 , y = 0

Thểtíchvậtthểtrònxoaykhi quay hìnhphẳnggiớihạnbởicácđường
quanhtrục ox là:
2
A. π (e + e)

2
B. π (e − e)

2
C. π e

D.

C©u 6 :

y=

Thểtíchvậtthểtrònxoaykhi quay hìnhphẳnggiớihạnbởicácđường
quanhtrục ox là:
A. 6π
C©u 7 :

π

4

1

∫ (1 − tan x) . cos

Giá trị của
A.

4

0

B.
d

∫
Nếu

d

∫

f ( x)dx = 5

a

;

x

dx

1
3

C.

b

, với

a
f ( x) =

∫ ttln

e

Hàm số

dt

x

đạt cực đại tại
B. 0

A. − ln 2

C©u 10 :

π
2

D.

thì

a

bằng:

C. 8

D. 0

C. ln 2

D. − ln 4

x=?

I = ∫ e sin x .sin x cos 3 xdx

Cho tích phân

0

2

. Nếu đổi biến số

1

1 t
e (1 − t )dt
2 ∫0

A.

I=

C.

I = 2 ∫ e t (1 − t )dt

B.

1

2

0

1
4

∫ f ( x)dx

B. 3
e2 x

1
2

b

f ( x)dx = 2

A. −2
C©u 9 :

D. 8π

bằng:

1
5

C©u 8 :

2

4
, y = 0 , x =1, x = 4
x

C. 12π

B. 4π

πe

D.

t = sin 2 x

thì

1
1

I = 2  ∫ e ttdtt+ ∫ e dt 
0
0


I=

1
1

1  tt
 ∫ e dtt+ ∫ e dt 
2 0
0


2

C©u 11 :

A. 2 + 2

B. 2

Diệntíchhìnhphẳnggiớihạnbởicácđường
x=2

y = x2

B.

C©u 13 :
Cho hìnhphẳng

( H)

8
3

giớihạnbởicácđường

A. 2π

B.

C©u 14 :

I=

Cho tích phân

3

3

( H)

y = sin x

∫
1

π2
2

C.

B.

t 2 dt
I=∫ 2
2 t +1

C©u 15 :
Diệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố
3−2 2

3

C©u 16 :
Tìmnguyênhàm:
53 5
x + 4 ln x + C
3

B.

∫(

3

π2
4

3 2 −1
3

x2 + 1
x

D.

π
2

D.

I=∫

thì

2

3

t dt
I=−∫ 2
t −1
2

x=0 y=0 x =π
;
;
và
.

t=

. Nếu đổi biến số

2

16
D. 3

quay quanh Ox bằng

1 + x2
dx
x2

2

3

2 2

,trụcOxvàđườngthẳng

C. 16

Thểtíchvậtthểtrònxoaysinhbởihình

A.

D.

là:

A. 8

A.

vàđồthịcủahaihàmsố y = cosx, y =

2

C.

C©u 12 :

A.

x =π

Diệntíchhìnhphẳnggiớihạnbởihaiđườngthẳng x = 0,
sinxlà:

3

3

C.

tdt
I= ∫ 2
t −1
2

y = x x2 + 1

C.

tdt
2 t +1
2

vàtrục ox vàđườngthẳng x=1 là:

2 2 −1
3

D.

3− 2
3

4
x 2 + ) dx
x
3

3 5
B. − 5 x + 4 ln x + C

3


C.

33 5
x − 4 ln x + C
5

C©u 17 :

π

∫ cos

Tíchphân
A.

−

2

D.

33 5
x + 4 ln x + C
5

C.

3
2

x sin xdx

0

bằng:

2
3

B.

2
3

C©u 18 :

D. 0

f ( x) =

Hàmsốnàosauđâykhônglànguyênhàmcủahàmsố
A.

x2 − x −1
x +1

B.

x2 + x + 1
x +1

C.

C©u 19 :
Diệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố

x (2 + x)
( x + 1)2

x2
x +1

y = x2 − 4x + 5

D.

x2 + x −1
x +1

vàhaitiếptuyếnvớiđồthịhàmsố tai

a
b

A(1;2) và B(4;5) cókếtquảdạng khiđó: a+bbằng
A. 12

B.

C©u 20 :

2 ln 2 + 6
9

1 − x2 + C

C©u 22 :

1

B.

Kếtquảcủa

4
5

D.

6 ln 2 − 2
9

x
∫ 1 − x2 dx

là:
6 ln 2 + 2
9

C.

2 ln 2 − 6
9

là:
B.

−1
1 − x2

+C

1

C.

1 − x2

+C

2
D. − 1 − x + C

F( x) = ln sin x − 3 cos x

Hàm số
đây:

4

D.

I = ∫ ( x 2 − 1) ln xdx

C©u 21 :

A.

C. 13

2

Giátrịcủatíchphân
A.

13
12

là một nguyên hàm của hàm số nào trong các hàm số sau

4


A.

f ( x) =

cos x + 3 sin x
sin x − 3 cos x

B.

C.

f ( x) =

− cos x − 3 sin x
sin x − 3 cos x

D.

C©u 23 :

e

I=∫
1

Giátrịcủatíchphân
A.

e2 − 1
2

là:
e2 + 1
2

π
4

I = ∫ sin 3x sin 2xdx = a + b
0

2
C. e + 1

2
2

Giảsử
1
A. − 6

C©u 25 :
Tìmnguyênhàm:

, khiđó, giátrịcủa
3
B. 10

∫ (x

2

A.

x3
4 3
+ 3ln x +
x +C
3
3

C.

x3
4 3
− 3ln x −

x +C
3
3

C©u 26 :

+

a+b

2
D. e

là:

3
C. − 10

3
− 2 x )dx
x

B.

x3
4 3
+ 3ln X −
x
3
3

D.

x3
4 3
+ 3ln x −
x +C
3
3

2
x
ln
+C
3 x+3

C.

1 x+3
ln
+C
3
x

∫ x( x + 3)dx

B.

1
x

− ln
+C
3 x+3

C©u 27 :
2

Diệntíchhìnhphẳnggiớihạnbởicácđường(P): y=2−x , (C): y=
A. 3 2 − 2π
5

1
D. 5

1

Tìmnguyênhàm:

A.

sin x − 3cos x
cos x + 3 sin x

f ( x) =

x 2 + 2 ln x
dx
x

B.

C©u 24 :

f ( x) = cos x + 3 sin x

π

B. 2 2 − 2

C.

8 2 π
−
3
2

1− x2

D.

1
x
ln
+C
3 x+3

và Oxlà:
D.

4 2 −π

5


C©u 28 :

y=x 2 ; y=

Diệntíchhìnhphẳnggiớihạnbởicácđồthịhàmsố
A.

27ln2-3

63
8

B.

C©u 29 :

C.

27ln2

A.

C.

2
1
x − 2 cos 2 x − sin 2 x + C

3
4

C©u 30 :

B.

2
1
x − 2 cos x + sin 2 x + C
3
4

D.

2
1
x − 2 cos x − sin 2 x + C
3
4

27ln2+1

;

;

;

;

2

I = ∫ 2 x x 2 − 1dx

Cho

1

và

A. I = ∫ udu
1

C©u 31 :

B.

5

2

Chưaxácđịnhđượ
c

. Chọnkhẳngđịnhsaitrongcáckhẳngđịnhsau:

I = ∫ udu

2

D.

2

. Giátrịcủa

B. 12

0

là:

C. 3

D. 6
y = 2x

y = x2

Diện tích hình phẳng giới hạn bởi đồ thị hàm số
B.

3

A = ∫ f ( x ) + g ( x )  dx

C©u 32 :
4
3

2 23
I= u
3

5

∫ g ( t ) dt = 9
,

2
I=
27
3

C.

0

5

∫ f ( x ) dx = 3
Cho biết

u = x2 − 1
3

2

3

2

C©u 33 :

C.

và đường thẳng
5
3

D.

là:
23
15

y = 2 x 2 - 4x - 6
Diệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố
x=-2 , x=-4 là

A. 12

6

D.

∫ (1 + sin x) dx

2
1

x + 2 cos x − sin 2 x + C
3
4

A.

là:

2

Tìmnguyênhàm:

A.

x2
27
; y=
8
x

B.

40
3

trục hoành và hai đường thẳng

C.

92

3

D.

50
3

6


C©u 34 :

0

3x 2 + 5x − 1
2
dx = a ln + b
x−2
3
−1

I= ∫

Giảsửrằng
A. 30
C©u 35 :
Kếtquảcủa
A.

∫ ln xdx

C. 50

B. Đápánkhác

C.

x ln x + C

B.

−5ln x +

5

∫(x +

Tìmnguyênhàm:
A.

B. 40

5ln x −

2

D.

1 x −3
ln

+C
3
x

2 5
x +C
5

1

1
x
ln
+C
3 x −3

B.

.

1 x+3
ln
+C
3
x

1
x
ln
+C

3 x+3

C.

C©u 38 :

y = x3

Diện tích hình phẳng giới hạn bởi các đường cong
A. −4

B.

C©u 39 :

π
2

∫ sin

Cho haitíchphân
π
2

∫ sin
0

7

x ln x − x + C

5
D. 5 ln x + 5 x + C

∫ x( x − 3)dx

Tìmnguyênhàm:

A.

D.

2

5
C. −5ln x − 5 x + C

A.

D. 60

x 3 ) dx

2 5
x +C
5

C©u 37 :

là:

là:

x ln x + x + C

C©u 36 :

. Khiđó, giátrịcủa

a + 2b

2

π
2

0

2

1
6

∫ cos

và

0

2

xdx > ∫ cos xdx

bằng:
D. 2

xdx

, hãychỉrakhẳngđịnhđúng:
B.

2

và

C. 0
π
2

xdx

y = x5

Không so sánhđược

0

7

π
2

C.

∫ sin

2

π
2

∫ cos

xdx <

0

π
2

2

xdx

D.

0

I = ∫ sin 2 xdx

0

Cho hai tích phân
I>J

B.

Hàmsố
A.

F( x) = e x

f ( x) = 2 xe

C©u 42 :

∫2

x

(

J = ∫ cos 2 xdx

và

0

. Hãy chỉ ra khẳng định đúng:

I=J

C.

I
B.

ln 2

f ( x) = e

2x

C.

ex
f ( x) =
2x

D.

f ( x) = x 2 e x − 1

2

dx

, kếtquảsai là:

)

x
B. 2 + C

π

I=∫
0

Cho tích phân
2
α

C. 2

x +1

+C

(

)

x
D. 2 2 + 1 + C

sin x
1 − 2α cos x + α 2

, với

α >1

B. 2α

C.

C©u 44 :

thì

I

bằng:

2

D.

α
2

y = x2 − 1 , y = x + 5

Diệntíchhìnhphẳnggiớihạnbởicácđồthịhàmsố
35
12

C©u 45 :

B.
d

∫
Nếu

A.

Không so sánh
được

2

C©u 43 :

A.

D.

lànguyênhàmcủahàmsố

x
A. 2 2 − 1 + C

A.

0

2

x2

x

Tính

xdx = ∫ cos 2 xdx

π
2

π
2

C©u 41 :

2

0

C©u 40 :

A.

∫ sin

π
2

-2

a

10
3

C.

d

∫

f ( x )dx = 5

,

cókếtquảlà
73
3

D.

73
6

b

∫ f ( x)dx

f ( x) dx = 2

b

với a < d < b thì
B. 0

a

C.

bằng
8

D. 3

C©u 46 : Kếtquảnàosaitrongcáckếtquảsao?
8

8


A.

dx
1
x
∫ 1 + cos x = 2 tan 2 + C

C.

∫ x ln x.ln(ln x) = ln(ln(ln x)) + C

dx

dx

B.

∫x

D.

∫ 3 − 2x

x2 + 1
xdx

2

=

1
ln
2

x2 + 1 − 1
x2 + 1 + 1

+C

1
= − ln 3 − 2 x 2 + C
4

C©u 47 : Diệntíchhìnhphẳnggiớihạnbởihaiđườngcong y = x3 – x và
y = x – x2 là :
A. Đápánkhác

B.

C©u 48 :
Tìmnguyênhàm:

∫ (x

3

−

37
6

33
C. 12

D.

2
+ x )dx

x

A.

1 4
2 3
x + 2 ln x −
x +C
4
3

B.

1 4
2 3
x − 2 ln x −
x +C
4
3

C.

1 4
2 3
x + 2 ln x +
x +C
4
3

D.

1 4
2 3
x − 2 ln x +
x +C
4
3

C©u 49 :

y= x

Cho hình phẳng giới hạn bởi các đường
khối tròn xoay tạo thành bằng:

π
A.

B.

37
12

π
6

y=x

và

quay xung quanh trục

C. 0

D.

C©u 50 :

Ox

. Thể tích

−π

y = x ,y =0, y = 2−x

Thểtíchvậtthểtrònxoaykhi quay hìnhphẳnggiớihạnbởicácđường
quanhtrục ox là:
A.

7π
12

C©u 51 :

3

Biếnđổi
A.

9

B. 6π

∫ 1+
0

f (tt) = 2 2 − 2t

x
1+ x

C.

35π
12

D.

6π
5

2

∫ f (t )dt

dx

thành
B.

1

f (tt) =

, với
2

+t

t = 1+ x

C.

f (t )

. Khiđó
f (tt) =

làhàmnàotrongcáchàmsốsau?
2

−t

D.

f (tt) = 2 2 + 2t

9

C©u 52 :

π

π

0

0

π

I = ∫ e x cos2 xdx J = ∫ e x sin 2 xdx

Cho
khẳng định sau?
(I)

;

K = ∫ e x cos 2 xdx

và

0

. Khẳng định nào đúng trong các

I + J = eπ

(II)

I−J=K

K=

(III)

eπ − 1
5

A. Chỉ (II)
C©u 53 :
Hàmsố

B. Chỉ (III)

y = tan 2 2x

C. Chỉ (I)

D. Chỉ (I) và (II)

nhậnhàmsốnàodướiđâylànguyênhàm?

A. 2 tan 2x + x

1
tan 2x − x

2

B.

C. tan 2x − x

D.

C©u 54 :

1
tan 2x + x
2

y = x 2;x = y2

Thểtíchvậtthểtrònxoangkhi quay hìnhphẳnggiớihạnbởiđồthịhàmsố
ox là
A.

π 2
10

4π
3

B.

C©u 55 :

π
6

I = ∫ sin n x cos xdx =
0

Cho
A. 3

Tìmnguyênhàm:

∫ (2 + e

4
1
3 x + e3 x + e 6 x + C
3
6
4

1

3x
6x
C. 4 x + 3 e − 6 e + C

10

3π
10

π

D. 10

n
. Khiđó bằng:

B. 4

C©u 56 :

A.

1
64

C.

quanhtrục

C. 6

D. 5

3x 2

) dx

B.

4
5
4 x + e3 x + e 6 x + C
3
6
4

1

3x
6x
D. 4 x + 3 e + 6 e + C

10


C©u 57 :

5

dx

∫ 2 x − 1 = ln K
1

Giảsử

K

. Giátrịcủa là:

A. 3

B. 8

C©u 58 :

C. 81

D. 9

y = x 3 + 11x - 6, y = 6x 2, x = 0, x = 2

Diệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố

dạng

a
b

có kết quả

khi đó a-b bằng

A. 2

B. -3

C©u 59 :

C. 3

D. 59

y = -x 2 + 4x
Diệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố

và các tiếp tuyến với đồ thị hàm số

biết tiếp tuyến đi qua M(5/2;6) có kết quả dạng
12

A. 11

B.

14

C.

a
b

khi đó a-b bằng
5

D. -5

C©u 60 : Diệntíchhìnhphẳnggiớihạnbởi (C): y= −x2+3x−2, d1:y = x−1 và d2:y=−x+2 cókếtquảlà

A.

1
8

B.

2
7

C.

1
12

D.

1
6

C©u 61 : Diệntíchhìnhphẳnggiớihạnbởiđườngcong y = x2 + 1, tiếptuyếnvớiđườngnàytạiđiểm M(2; 5)
vàtrục Oy là:
A.

7
3

B.

C©u 62 :

C. 2

D.

8
3

1

I = ∫ x.e − x dx

Giátrịcủa

C©u 63 :

∫
Tính

0

là:
2
B. 1 − e

A. 1

11

5

3

C.

2
e

D. 2e − 1

dx
1− x

, kếtquảlà:
11


A.

C
1− x

B.

−2 1 − x + C

2

C.

C©u 64 :

1− x

+C

y = (e + 1)x
Diệntíchhìnhphẳnggiớihạnbởicácđồthịhàmsố
e

A. 2 − 2

B. 2

125
24

B.

125
34

vàtrụchoànhlà:
C.

125
14

28
3

B.

25
3

C©u 67 :

vàpatabol

C.

22
3

55
6

C©u 68 :
Tìmnguyênhàm:

12

x2
y=
2

125
44

bằng:

D.

26
3

y = x2 − 4 x + 3

Diệntíchhìnhphẳnggiớihạnbởicácđồthị:

A.

D.

y =4− x

Diệntíchhìnhphẳnggiớihạnbởiđườngthẳng

A.

D.

3
−1
e

y = −2 x 2 + x + 3

C©u 66 :

A.

là:

e
−1
2

Diệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố
A.

y = (1 + ex )x

và
C.

C©u 65 :

D. C 1 − x

B.

∫ (x

2

+

3
1

x − 2 s inx + sin 2 x + C
2
4

205
6

và y=x+3 cókếtquảlà:
C.

109
6

B.

3
1
x + 2s inx- sin 2 x + C
2
4

D.

126
5

3
− 2 x )dx
x

12


C.

3
1
x + 2 cos x + sin 2 x + C
2
4

3
1
x + 2s inx + sin 2 x + C
2
4

D.

C©u 69 :

y=x

y = x + sin x

Diện tích hình phẳng giới hạn bởi các đường cong
bằng:
A. −4
C©u 70 :
Cho

y=−

là mộtnguyênhàmcủahàmsố
B. − tan x + 1

A. − tan x

, với

C. 0

B. 4
F( x)

và

1
cos 2 x

và

0 ≤ x ≤ 2π

D. 1
F ( 0) = 1

. Khiđó, ta có

C. tan x + 1

F( x)

là:

D. tan x − 1

C©u 71 :

y2 = 8x

Thểtíchvậtthểtrònxoaykhi quay hìnhphẳnggiớihạnbởicácđồthịhàmsố
trục ox là:
A. 12π

C. 16π

B. 4π

D. 8π

C©u 72 :
Thểtíchvậtthểtrònxoaykhi quay hìnhphẳnggiớihạnbởicácđường

cókếtquảdạng

aπ
b

A. 11

và x=2 quanh

y = 1 − x2 , y = 0

quanhtrục ox

khiđóa+bcókếtquảlà:
C. 31

B. 17

C©u 73 :

D. 25

2

Nguyênhàm

F( x)

củahàmsố

x3 1
− + 2x + C
3 x

A.

F ( x) =

C.

x3
+x
F( x) = 3 2 + C
x
2

 x2 + 1 
f ( x) = 
÷
 x 

làhàmsốnàotrongcáchàmsốsau?
x3 1
+ + 2x + C
3 x

B.

F ( x) =

D.

 x3

 +x÷
F ( x) =  3 2 ÷ + C

 x ÷

÷
 2 

3

C©u 74 : Diệntíchhìnhphẳnggiớihạnbởicácđường(P): y =x2-2x+2 vàcáctiếptuyếnbới (P)
biếttiếptuyếnđi qua A(2;-2)là:

13

13


A.

8
3

64
3

B.

C.

16
3

D.

40
3

C©u 75 : Thểtíchkhốitrònxoaytạonênkhi quay quanhtrục Ox hìnhphẳnggiớihạnbởicácđường y =(1x)2, y = 0, x = 0 và x = 2 bằng:
A. 2π

B.

8π 2
3

C.

5π
2

D.

2π
5

C©u 76 : Thểtíchkhốitrònxoayđượctạobởiphép quay quanhtrục Ox hìnhphẳnggiớihạnbởicácđường y
= x2và x = y2bằng:
A. 10π
C©u 77 :

B.
2

∫ 2e
Giá trị của

2x

0

10π
3

D.

4
C. e

4
D. 3e

dx

bằng:

4
A. e − 1

4
B. 4e

C©u 78 :

y = - x 3 + 3x + 1
Diệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố

A.

3π
10

C. 3π

57
4

B.

45
4

và đường thẳng y=3 là
C.

27
4

D.

21
4

C©u 79 : Tìmkhẳngđịnhsaitrongcáckhẳngđịnhsau:
π

A.

x
∫0 sin 2 dx = 2 ∫0 sin xdx
1

C.

14

π
2

B.

0

∫ (1 + x) dx = 0

D.

x

0

1

1

∫ sin(1 − x)dx = ∫ sin xdx
0

1

∫x

−1

2007

(1 + x)dx =

2
2009

14


15

15


ĐỀ SỐ 02
C©u 1 :
Tính
A.

C©u 2 :

ex

2

+1

∫ x.e

x 2 +1

dx

+C

B.

, trục hoành,

5

ò
2

ò 2e

(

)

5

2

ò( x - 1) dx

C. pò y + 1 dx

D.

4
C. 4e

4
D. 3e - 1

2

1

2

dx

0

là:
4
B. e - 1

C©u 4 :

π

I =∫4
0

Cho tích phân
I=

I=

4 2
2u 2 + 1) du
(
∫
1
3
4 2 2
( u − 1) du
3 ∫1

C©u 5 :

6 tan x
dx
cos x 3 tan x + 1
2

B.

D.

.
4

ò f (x)dx = 10
0

và
B.

0

Họ nguyên hàm của hàm số
1 − x2 + C

4

17

4 2 2
( u + 1) du
3 ∫1

I=

.

4 2
( 2u 2 − 1) du
3 ∫1

I=

.

bằng :
C.

f ( x) =

)

thì ta được:

ò f (x)dx
, thì

C©u 6 :

(

u = 3 tan x + 1

6

ò f (x)dx = 7

3

1 2
x +2
3

. Giả sử đặt

.

6

Nếu

16

3

2

4
A. e

A.

2

2

Giá trị của

A.

D.

1 x 2 −1
e +C
2

quanh trục Ox bằng:

B. pò ( x - 1) dx

x - 1dx

2x

C.

x = 2, x = 5
5

C©u 3 :

A.

C.

1 x 2 +1
e

+C
2

Thể tích của khối tròn xoay tạo thành khi quay hình phẳng D giới hạn bởi các đường

y = x- 1

A.

1 x2
e +C
2

170

D.

- 3

x3
1 − x2

là:
B.

−

(

)

1 2
x +1
3

1 − x2 + C

16


C.

(

)

1 2
x +1
3

C©u 7 :

5

dx

ò 2x Giả sử

2
2

D. − 3 ( x + 2 ) 1 − x + C

1

1 − x2 + C

1

1

= lnc
. Giá trị đúng của

A. 9
Tính diện tích
y = 4−

C. 81

S = 2π +

( S)

x2
x2
;y=
4
4 2
2
3

.
S = 2π +

B.

.

ff(1) = 12,

'(x)

C.

.

S = 2π +

29

ò f '(x)dx = 17
liên tục và

1

, giá trị của

5

B.

C©u 10 :

C.

4

Nếu

4
3

D.

.

S = 2π +

1
3

.

f (x)

liên tục và
B.

f (4)

bằng:

19

D.

9

D.

9

2

ò f (x)dx = 10

5

C©u 11 :

0

ò f (2x)dx
, thì

0

29

bằng :

C.

19

b

Biết

∫0 ( 2 x − 4 ) dx = 0

A.

b =1

C.

b =1

C©u 12 :

hoặc
hoặc

, khi đó b nhận giá trị bằng:

b=4

B.

b=0

b=2

D.

b=0

p
6

I = ò sinn x cosxdx =

Cho
A. 5
17

5
3

4

Nếu

A.

D. 8

hình phẳng được giới hạn bởi các đường:

C©u 9 :

A.

là:

B. 3

C©u 8 :

A.

c

0

1
64

. Khi đó
B. 3

n

hoặc
hoặc

b=2
b=4

bằng:

C.

4

D. 6
17


C©u 13 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số

23
A. 15

B.

4
3

y = x2

và đường thẳng

3
C. 2

y = 2x

bằng:

5
D. 3

C©u 14 :

y = − x2 + 2

Thể tích của khối tròn xoay tạo lên bởi lên hình phẳng (H) giới hạn bởi các đường
y =1

;

và trục Ox khí quay xung quanh Ox là
1

1

−1

−1

1

1

−1

−1

A.

π ∫ (− x 2 + 1) 2 dx + π ∫ dx

C.

π ∫ (− x 2 + 2) 2 dx − π ∫ dx

C©u 15 :

f ( x) =

Cho
A. m = −

D.

B.

m=

3
4

C. m = −
3

ab=
.
64

B.

D.

ab=
.
46

ln xdx =

1

C.

3ea +1
b

m=

π  π
F  ÷=
4 8

4
3

?

a- b = 12

D.

a- b = 4

D.

a> 2

1

a= 2

B.

C©u 18 :

f ( x) =
F ( x)

a= 4

x3
1
ò x4 +1dx = a ln2
0

C.

(

f ( x)

là một nguyên hàm của hàm số

a = 4; b = 2; c = 1
a = 4; b = −2; c = 1

)

x>

2x − 3

với

3
2

. Để hàm số

a , b, c

thì giá trị của
B.

.

?

a< 4

20 x 2 − 30 x + 7
F ( x ) = ax 2 + bx + x
2x − 3

;

Cho các hàm số:

18

3
4

e

òx

Khẳng định nào sau đây đúng về kết quả

C.

−1

. Tìm m để nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 và

C©u 17 :

A.

−1

π ∫ (− x 2 + 2) 2 dx

Khẳng định nào sau đây đúng về kết quả

A.

−1

B.

C©u 16 :

A.

1

1

4m
+ sin 2 x
π

4
3

1

π ∫ (− x 2 + 2) 2 dx + π ∫ dx

D.

là:

a = 4; b = −2; c = −1
a = 4; b = 2; c = −1

18


C©u 19 :

1

I =∫
0

Tính tích phân
4

5

(3x − 1)dx
x2 + 6x + 9

3
4

A. 3ln 3 + 6

B. 3ln +

C©u 20 :

ò (x -

2)sin3xdx = -

Một nguyên hàm
A.

S = 14

F ( x) = ∫

Tìm họ nguyên hàm:

(x - a)cos3x 1
+ sin3x + 2017
b
c

C.

1

S =3

D.

bằng :

S = 10

1

f ( x ) = x 2 – 3x +

Nguyên hàm của hàm số

F(x) =

thì tổng

S = ab
. +c

D. F ( x) = 2 2 ln x + 1 + C

C©u 22 :

C.

D.

B. F ( x) = 2 ln x + 1 + C

C. F ( x) = 4 2 ln x + 1 + C

F(x) =

4 7
3ln −
3 6

dx
x 2 ln x + 1

A. F ( x) = 2 2 ln x + 1 + C

A.

5

C. 3ln 3 − 6

S = 15

B.

C©u 21 :

4

5
6

x3 3x 2
−

− ln x + C
3
2
x3 3x 2
−
+ ln x + C
3
2

1
x

là
B.
F(x) =
D.

F(x) =

x 3 3x 2
−
+ ln x + C
3
2
x3 3x 2
+
+ ln x + C
3
2

C©u 23 : Thể tích của khối tròn xoay sinh ra khi quay quanh trục Oy hình phẳng giới hạn bởi các
đường:
A.

16π
5

C©u 24 :

19

và Ox bằng:

B. 5π
f ( x) =

Cho
A.

y = x 2 − 4x + 3

2x
x +1

C.

π
5

B.

2
∫ f ( x ) dx = 3ln ( 1 + x ) + C

D.

16π
3

2

. Khi đó:

2
∫ f ( x ) dx = 2 ln ( 1 + x ) + C

19


C.

2
∫ f ( x ) dx = 4 ln ( 1 + x ) + C

D.

2
∫ f ( x ) dx = ln ( 1 + x ) + C

C©u 25 : Cho hai hàm số y = f(x), y = g(x) có đồ thị (C1) và (C2) liên tục trên [a;b] thì công thức tính

diện tích hình phẳng giới hạn bởi (C1), (C2) và hai đường thẳng x = a, x = b là:
b

b

∫ [ f (x) − g(x)] dx

A.

S=

C.

S = ∫ f (x)dx − ∫ g(x)dx

a

b

b

a

a

0

Khẳng định nào sau đây sai về kết quả
ab
. = 3(c +1)

1

I =∫

Tính tích phân
A. 5ln 2 − 3ln 2
C©u 28 :
Cho hàm

ac = b+ 3

B.

C©u 27 :

0

S = ∫ [ g(x) − f (x) ] dx

D.

S = ∫ f (x) − g(x) dx

a

b

C©u 26 :

A.

B.

a

x +1
b
dx = a ln - 1
2
c

ò x- 1

C.

?

a + b+ 2c = 10

D.

ab = c +1

( x + 4) dx
x 2 + 3x + 2

B. 5ln 2 + 2 ln 3

f ( x ) = sin 4 2 x

C. 5ln 2 − 2ln 3

D. 2 ln 5 − 2 ln 3

. Khi đó:

1

1

1

1



A.

∫ f ( x ) dx = 8  3x + sin 4 x + 8 sin 8 x ÷ + C

C.

∫ f ( x ) dx = 8  3x + cos 4 x + 8 sin 8 x ÷ + C



1

1



1

1



B.

∫ f ( x ) dx = 8  3x − cos 4 x + 8 sin 8x ÷ + C

D.

∫ f ( x ) dx = 8  3x − sin 4 x + 8 sin 8x ÷ + C

C©u 29 : Cho hàm số y = f(x) liên tục và chỉ triệt tiêu khi x = c trên [a; b]. Các kết quả sau, câu nào
đúng?
b

A.

∫
a

b

20

∫
a

B.

a

b

C.

b

f (x) dx ≥ ∫ f(x)dx

c

f (x) dx =

∫
a

b

f(x) dx + ∫ f (x)dx

∫
a

c

b

a

c

f (x) dx = ∫ f(x) dx + ∫ f(x) dx

D. A, B, C đều đúng

a

20


C©u 30 :
Diện tích phẳng giới hạn bởi:
A.

4
3

x = −1; x = 2; y = 0; y = x 2 − 2 x

B. 1

C.

C©u 31 :

Tìm một nguyên hàm F(x) của hàm số
2
2
F(x)
=
x
+
x
+
−6
A.
x +1

C.

F(x) =

x2
2
13
+x+
−
2
x +1 6

C©u 32 :
Tính diện tích
A.

( S)

C©u 33 :

D.

0

x 3 + 3x 2 + 3x − 1
f (x) =
x 2 + 2x + 1

biết

B.

F(x) = x 2 + x +

D.

F(x) =

1
3

2
13
−
x +1 6

x2

2
+x+
−6
2
x +1

hình phẳng được giới hạn bởi các đường:
B.

∫ 2008 dx = F ( x ) + C

8
23
S = ln 2 −
3
18

C.

8
17
S = ln 2 −
3
18

x

Gọi

F(1) =

y = x 2 ; y = ln

8
31
S = − ln 2 +
3
18

x

A. 2008 ln 2008

, với C là hằng số. Khi đó hàm số

B. 2008

x+1

C. 2008

8
3

F ( x)

x

1
;x =1

x +1

D.

8
23
S = ln 2 +
3
18

D.

2008 x
ln 2008

bằng

C©u 34 : Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi các đường

y = x ln x, y = 0, x = e
A. a=27; b=5
C©u 35 :

B. a=24; b=6

trong đó a,b là hai số thực nào dưới đây?

C. a=27; b=6

D. a=24; b=5

y = f ( x)
Cho đồ thị hàm số

21

có giá trị bằng:

π
(b e3 − 2)
a

. Diện tích hình phẳng (phần tô đậm trong hình) là:

21


4

A.

ò f ( x) dx
1

C.

4

ò f ( x) dx + ò f ( x) dx
- 3

C©u 36 :
Diện tích hình phẳng giới hạn bởi hai đường cong
A.

e
−1
2

e
−2
2

B.
( đvdt)

C©u 37 :

C.
( đvdt)

- 3

4

- 3

4

0

0

ò f ( x) dx + ò f ( x) dx

D.

1

0

ò f ( x) dx + ò f ( x) dx

B.

- 3

0

y = (1 + e x ) x

e
+2
2

và

y = (e + 1) x

là?

e
+1
2

D.
( đvdt)

( đvdt)

p

ò cos x.sin xdx
2

Tích phân

0

bằng:

2
A. - 3

2
3

B.

C©u 38 :

C.

3
2

D. 0

π

Cho tích phân

I = ∫ 2 sin 2 x.esin x dx
0

: .một học sinh giải như sau:
x=0⇒t =0

Bước 1: Đặt

t = sin x ⇒ dt = cos xdx

Bước 2: chọn

x=

. Đổi cận:

π
1

⇒ t = 1 ⇒ I = 2 t.et dt
∫0
2

.

 u =t
du = dt
⇒

t
t
dv = e dt  v = e

1

1

1

1

0

0

0

0

⇒ ∫ t.et dt = t.et − ∫ et dt = e − et = 1
1

Bước 3:
22

I = 2∫ t.et dt = 2
0

.
22


Hỏi bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
A. Bài giải trên sai từ bước 1.
B. Bài giải trên sai từ bước 2 .
C.

D.

Bài giải trên hoàn toàn đúng.

C©u 39 :
Cho hình phẳng giới hạn bởi:

Bài gaiir trên sai ở bước 3.

π



D =  y = tan x; x = 0; x = ; y = 0 
3



Thể tích vật tròn xoay khi D quay quanh Ox:
π

π 3+ ÷
A.
3


3−

B.

π
3

C.

C©u 40 :
Nguyên hàm của hàm số

y = 3x - 1

2
C. 9

( 3x - 1)

3

+C

C©u 41 :

æ
1
ç
; +¥
ç
ç
è3

trên

1

2

∫

D.

π

π 3− ÷
D.

3


π
3

ö
÷
÷
÷
÷
ø
là:

2
B. 9

3 2
x - x +C
2

A.

3+

( 3x - 1)

3

+C

3 2
x - x +C
2

1 − x 2 dx

0

Cho tích phân
A.

π
3
 −
÷
÷
6 4 

bằng:
B.

1π
3
 −
÷
2 6 4 ÷


C.

π
3
 +
÷
÷
6 4 

C©u 42 :
Tính diện tích hình phẳng tạo bởi các đường: Parabol
các điểm
A.

S=

A ( 1; 2 ) , B ( 4;5 )

7
2

B.

nằm trên
S=

11
6

( P)

D.

( P ) : y = x2 − 4x + 5

1π
3
 +
÷
2 6 4 ÷


và 2 tiếp tuyến tại

.
C.

S=

9
4

D.

S=

13
8

C©u 43 : Tìm hàm số F(x) biết rằng F’(x) = 4x3 – 3x2 + 2 và F(-1) = 3

23

A. F(x) = x4 – x3 - 2x -3

B. F(x) = x4 – x3 - 2x + 3

C. F(x) = x4 – x3 + 2x + 3

D. F(x) = x4 + x3 + 2x + 3
23


C©u 44 :

π

I = ∫ 1 + cos 2x dx
0

A.

bằng:

2

B. 0

C©u 45 :

F ( x) = ∫

Tìm họ nguyên hàm:
A.

C.
C©u 46 :

1

4
B. F ( x ) = 4 ln x − 1 + C

1
ln x 4 − 1 + C
2

9

9

0

9

ò[ 2 f (x) + 3g(x)] dx

ò g(x)dx = 16
0

và

122

thì

0

bằng :

74

B.

D.

53

π
3

Biết rằng

π π
∀x ∈  ; 
4 3

3
1
≤I≤
12

4

3 cot x 4
≤
≤ .
π
x
π

thì

cot x
dx.
x
π

I=∫
4

Gọi

1
1
≤I≤
4
3

B.

C©u 48 :

C.

Kết luận nào sau đây là đúng ?
1
1
≤I≤
5
4

D.

3
1
≤I≤
12
3

1

∫x
Giá trị của tích phân

3
A. 16

C©u 49 :

ò2

(

33

1 − x 4 dx.

0

B. 2

x

ln2
x

Tính

)

x
A. 2 2 + 1 +C

24

48

C.

C©u 47 :

A.

1
F ( x ) = ln x 4 − 1 + C
3

D.

ò f (x)dx = 37
Nếu

A.

x3
dx
x4 −1

F ( x) = ln x 4 − 1 + C

F ( x) =

D. 2 2

C. 2

bằng?
6
C. 13

D. Đáp án khác

dx
, kết quả là:
x
B. 2 +C

(

)

x
C. 2 2 - 1 +C

x +1
+C
D. 2

24


C©u 50 :

dx

ò

1- x

Tính
A.

, kết quả là:

C

B. - 2 1- x +C

1- x

C©u 51 :

y=

4 − x2

π
B. 2 ln 2 − 2 − 4

C©u 52 :
f (x) =

(

D. C 1- x

và trục hoành là:
π
D. 2 ln 2 − 2 − 3 + 3

)

x2 +1

là:

)

(

1- x

+C

π
C. ln 2 − 2 − 3 + 3

x ln x + x 2 + 1

Một nguyên hàm của
A.

C.

x ln(x + 2)

Diện tích hình phẳng giới hạn bởi
π
A. 2 − 3 + 3

2

x ln x + x 2 + 1 − x + C

B.

2
C. x ln x + 1 − x + C

)

(

ln x + x 2 + 1 − x + C

(

)

x 2 + 1 ln x + x 2 + 1 − x + C

D.

C©u 53 : Cho hình phẳng giới hạn bởi các đường y = 2x – x2 và y = 0. Thì thể tích vật thể tròn xoay
được sinh ra bởi hình phẳng đó khi nó quay quanh trục Ox có giá trị bằng?
16π
A. 15

(đvtt)

15π

B. 16

C.
(đvtt)

C©u 54 :

p
2

5π
6

ò (2x - 1Khẳng định nào sau đây sai về kết quả
A.

a + 2b = 8

B.

a+ b = 5

C©u 55 :
Một nguyên hàm của hàm số
1
−
cos3 x
A.
3

C©u 56 :

x

ò
Nếu

25

a

B.

(đvtt)

(đvtt)

æp 1ö
sin x)dx = pç
- ÷
÷
ç
÷- 1
ç
èa bø

?
C.

2a- 3b = 2

D.

a- b = 2

y = sin 3 x

−3cos3 x

f (t)
dt + 6 = 2 x, x > 0
t2

0

D.

6π
5

thì hệ số

C.

a

3cos3 x

D.

1
cos3 x
3

bằng :
25