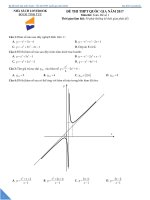
350 câu trắc nghiệm chuyên đề hàm số ôn thi thpt quốc gia (file Word có đáp án)

Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (440.01 KB, 52 trang )

NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT

CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN
(ĐỀ 001-KSHS)
C©u 1 :

y = x3 - 3x2 - 9x + 35
Giátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố

A.
C©u 2 :

20;- 2

10;- 11

B.

C.

B.

Đồthịcủahàmsố f(x) cóđúng 1 điểmuốn
C. Đồthịhàmsố qua A(0;-2017)
C©u 3 :

( - 1;0)

lim f ( x ) = +∞ va lim f ( x ) = +∞
x →+∞

x →−∞

D. Hàmsố y = f(x) có 1 cựctiểu

A. Đápánkhác.

( - 1;0) ( 1;+¥ )

B.

Tìm mlớnnhất để hàm số

và

m=3

B.

Xácđịnh m đểphươngtrình
m>1

C.

( 1;+¥ )

1
y = x3 − mx 2 + (4m − 3) x + 2016
3

C©u 5 :

C.

x3 - 3mx + 2 = 0

B.

C©u 6 :

m<2

D.

"x Î ¡

đồng biến trên tập xác định của nó.

m=1

D.

m=2

D.

m<- 2

cómộtnghiệmduynhất:
C.

m<1

y = 4 − x2 + x
Tìmgiátrịlớnnhấtcủahàmsố

1

40; 31

đồngbiếntrêncáckhoảngnào?

C©u 4 :

A.

D.

y = x4 - 2x2 + 1
Hàmsố

A.

40;- 41

Cho hàmsố y = x4 + 2x2 – 2017. Trongcácmệnhđềsau ,mệnhđềnàosai ?

A.

A.

é- 4;4ù
ê
ú
ë
û
trênđoạn
lầnlượtlà:

Maxf ( x ) = f ( 4 ) =
 1 
 − 3;3

1
− ln 2
2

.
B.

Maxf ( x ) = f ( 1) =
 1 
 − 3 ;3

1
− ln 2
2

1

C.

Maxf ( x ) = f ( 2 ) =
 1 
 − 3 ;3

193
100

D.

C©u 7 :

Maxf ( x ) = f ( 1) =
 1 
 − 3 ;3

1
5

y = ax 3 + bx 2 + cx + d
Cho cácdạngđồthịcủahàmsố

A

nhưsau:

B

C

D

Vàcácđiềukiện:

1.

3.

a > 0
 2
 b − 3ac > 0

2.

a < 0
 2
 b − 3ac > 0

4.

a > 0
 2
 b − 3ac < 0
a < 0
 2
 b − 3ac < 0

Hãychọnsựtươngứngđúnggiữacácdạngđồthịvàđiềukiện.
A.

A → 2; B → 4;C → 1; D → 3

B.

A → 3; B → 4;C → 2; D → 1

C.

A → 1; B → 3;C → 2; D → 4

D.

A → 1; B → 2;C → 3; D → 4

C©u 8 :
Tìm
2

m

y=

d : y = x +m
để đường thẳng

cắt đồ thị hàm số

2x
x +1

tại hai điểm phân biệt.
2

A.

ém > 3 + 3 2
ê
ê
êm < 3 - 3 2
ë

B.

C©u 9 :

ém > 3 + 2 2
ê
ê
êm < 3 - 2 2
ë

C.

ém > 1+ 2 3
ê
ê
êm < 1- 2 3
ë

C.

6

D.

ém > 4 + 2 2
ê
ê
êm < 4 - 2 2
ë

y = 2x + 5 − x2
Tìm GTLN củahàmsố

A.

5

B.

C©u 10 :

−2 5

D. Đápánkhác

1
2
y = x3 − mx 2 − x + m +

3
3

Cho hàmsố
(Cm). Tìm m để (Cm) cắttrục Ox
tạibađiểmphânbiệtcóhoànhđộx1 ; x2 ; x3thỏa x12 + x22 + x32> 15?
A. m < -1 hoặc m > 1

C. m > 0

B. m < -1

C©u 11 :

y = x 4 − 2( m 2 + 1) x 2 + 1
Tìmcácgiátrịcủathamsốm đểhàmsố
điểmcựctrịthỏamãngiátrịcựctiểuđạtgiátrịlớnnhất.

A.
C©u 12 :

m = −1

B.

m=0

có 3
m=3

C.

D.

A. A(0;1) ; B(1;-1) ; C(2;-3)

B. A(0;1) ; B(1;-1) ; C(-2;3)

C. A(-1;1) ; B(2;0) ; C(3;-2)

D. Đápánkhác

y = ax 3 + bx 2 + cx + d
Hàmsố

A.

đạtcựctrịtại

a > 0, b < 0,c > 0

C©u 14 :

y=
Hàmsố

A.

mx + 1
x+m

−1 < m < 1

C©u 15 :

y=Hàmsố

A.

m=1

Họđườngcong (Cm) : y = mx3 – 3mx2 + 2(m-1)x + 1 đi qua nhữngđiểmcốđịnhnào?

C©u 13 :

3

D. m > 1

m>1

B.

x1 , x2

b 2 − 12ac > 0

nằmhaiphíatrụctungkhivàchỉkhi:

a

C.

c

và tráidấu

D.

b2 − 12ac ≥ 0

m ∈ ¡ \ [ − 1;1]

D.

m ≥1

D.

m³ 2

(1; +∞)
đồngbiếntrênkhoảng
B.

m >1

1 3
x + ( m - 1) x + 7
3

B.

m£ 1

khi:
C.

nghịchbiếntrên
C.

¡

thìđiềukiệncủa m là:

m=2

3

C©u 16 :

y=
Đồthịcủahàmsố

A.

2x − 1
x − x −1
2

0

C©u 17 :

cóbaonhiêuđườngtiệmcận:
C. 2

B. 1

y = ax 4 + bx 2 + c
Hàmsố

A(0; −3)
đạtcựcđạitại

D. 3

B( −1; −5)
vàđạtcựctiểutại

Khiđógiátrịcủa a, b, c lầnlượtlà:
A. 2; 4; -3
C©u 18 :

B. -3; -1; -5

C. -2; 4; -3

D. 2; -4; -3

Cho đồthị (C) : y = ax4 + bx2 + c .Xácđịnhdấucủa a ; b ; c biếthìnhdạngđồthịnhưsau :

A. a > 0 và b < 0 và c > 0

B. a > 0 và b > 0 và c > 0

C. Đápánkhác

D. a > 0 và b > 0 và c < 0

4 x2 ( 1 − x2 ) = 1 − k

C©u 19 :
Tìmtấtcảcácgiátrịcủathamsốkđểphươngtrìnhsaucóbốnnghiệmthựcphânbiệt
A.

0
B.

0 < k <1

C©u 20 :

C.

−1 < k < 1

C©u 21 :

D.

k <3

f ( x) = x3 + 2 x 2 + x − 4
Viếtphươngtrìnhtiếptuyếndcủađồthịhàmsố
ụchoành.

A.

.

y = 2 x −1

B.

y = 8x − 8

tạigiaođiểmcủađồthịhàmsốvớitr

C.

y =1

D.

y = x−7

Tìmgiátrịnhỏnhấtcủahàmsố:

y = 1 + x + 3 − x − x + 1. 3 − x

4

4

A.

yMin = 2 2 − 1

C©u 22 :

y=
Hàmsố

A.

yMin = 2 2 − 2

B.

x3
− 3x 2 + 5 x − 2
3

( 2;3)

C.

y=
Chọnđápánđúng. Cho hàmsố

A.

C.

9
10

D.

yMin =

8
10

( −∞;1)

va ( 5; +∞ )

D.

( 1;6 )

D.

y + 2= −3( x − 1)

D.

y =1

, khiđóhàmsố:
B.

Nghịchbiếntrên

( 2; +∞ )

D.

Đồngbiếntrên

R \{ 2}
Đồngbiếntrên

R \{ 2}
Nghịchbiếntrên

f ( x ) = x 3 − 3x 2
Cho hàmsố

A.

2x + 1
2−x

( 2; +∞ )

C©u 24 :

yMin =

nghịchbiếntrênkhoảngnàotrongcáckhoảngsauđây?

B. R

C©u 23 :

C.

, tiếptuyếncủađồthịcóhệsốgóc k= -3 là

y − 2− 3( x − 1) = 0

y = −3( x − 1) + 2

B.

C©u 25 :

y=

C.

y − 2= −3( x − 1)

x+3
x2 + 1

Tìmcậnngangcủađồthịhàmsố
A.

y=3

y=2

B.

C©u 26 :

y=
Đồthịhàmsố

2x + 1
x- 1

C.

y = 1;y = - 1

( C)
là

( C)
. Viếtphươngtrìnhtiếptuyếtcủa

biếttiếptuyếnđó song

( d) : y = - 3x + 15
songvớiđườngthẳng
A.
C.

y = - 3x - 1

y = - 3x + 11; y = - 3x - 1

C©u 27 :

y=
Cho hàmsố

5

2x +1
(C )
x +1

B.

y = - 3x + 11

D.

y = 3x + 11

. Tìmcácđiểm M trênđồthị (C) saochotổngkhoảngcáchtừ M
5

đếnhaiđườngtiệmcậnlànhỏnhất
A. M(0;1) ; M(-2;3)

C.

B. Đápánkhác

C©u 28 :

M = 11, m = 2

B.

Tìmcácgiátrịcủathamsốmđểhàmsố
m>

1
3

B.

trên

M = 3, m = 2

C©u 29 :

A.

[ 0; 2]

y = x4 − 2x2 + 3
Tìmgiátrịlớnnhất M vàgiátrịnhỏnhất m của

A.

m<

C.

C.

:

M = 5, m = 2

x3
y = − ( m − 1) x 2 + mx + 5
3

1
2

D. M(0;1)

M(3;2) ; M(1;-1)

D.

M = 11, m = 3

có 2 điểmcựctrị.

3≥m≥2

D.

m=1

C©u 30 :
Cho hàmsố y = 2x3 – 3x2 + 5 (C). Viếtphươngtrìnhtiếptuyếncủađồthị (C) biếttiếptuyến qua
vàtiếpxúcvới (C) tạiđiểmcóhoànhđộlớnhơn 1
A. y = 12x - 15

−

C.

B. y = 4

21
645
x+
32
128

19
A( ; 4)

12

D. Cảbađápántrên

y=
C©u 31 :

A.

y = x 3 + 3x 2 − 9x + 1
Tâmđốixứngcủađồthịhàmsố

là :

I ( −1; 6)

C.

C©u 32 :
Địnhmđểhàmsố
A.

B.

I (3; 28)

x3 mx 2 1
y= −
+
3

2
3

m=3

B.

C©u 33 :

đạtcựctiểutại

m=2

D.

I ( −1; 12)

C. Đápánkhác.

D.

m=1

C.

D. 3

x=2

I (1; 4)

.

f ( x ) = x 4 − 2x 2 + 1
Tìmsốcựctrịcủahàmsốsau:

A. Cảbađápán A, B, C

B.

y=1; y= 0

x=0; x=1; x= -1

C©u 34 :

x=

y = sin3x + msinx
Vớigiátrịnàocủa m thìhàmsố
A.
6

m= 5

B. - 6

đạtcựcđạitạiđiểm
C.

6

p
3

?
D. - 5
6

C©u 35 :

y=
Tiệmcậnngangcủađồthịhàmsố

A.

y = −3

2x + 1
x −1

là:

x =1

B.

x=−

C.

C©u 36 :

f (x ) =

1
2

D.

y=2

x 2 − 5x + 2
− x2 + 4 x − 3

Tìmtiêmcậnđứngcủađồthịhàmsốsau:
A. y= -1

C. x=1; x= 3

B. y=1; x=3

C©u 37 :

y = x2 − 4x + m − 3
Điềukiệncầnvàđủđể

A.
C©u 38 :

m≤7

xácđịnhvớimọi
m>7

B.

1
2
3

Nếu

Hàmsố

x0

đạtcựcđạitại khivàchỉkhiđạohàmđổidấutừdương sang âmqua
x0
x0
Hàmsố
đạtcựctrịtại khivàchỉkhi lànghiệmcủađạohàm.
y = f ( x)
f '( xo ) = 0 f '' ( x0 ) = 0 x0
Nếu
và
thì khôngphảilàcựctrịcủahàmsố
đãcho.

f '( xo ) = 0

f '' ( x0 ) > 0
và

thìhàmsốđạtcựcđạitại
B. 1, 2, 4

C©u 39 :

f (x ) =
Tìmsốtiệmcậncủahàmsốsau:

A. 4
C©u 40 :

x0

x0

.

.

C. 1

D. Tấtcảđềuđúng

C.

D. 3

x 2 − 3x − 1
x 2 − 3x − 4

B. 2

1

y = 2x 4 − 4x 2
Cho hàmsố

7

m≥7

y = f ( x)

A. 1,3,4 .

B.

D.

Phátbiểunàosauđâylàđúng:

y = f ( x)

A.

x = ±1; x = ±3

x∈¡ :

m<7

C.

D.

. Hãychọnmệnhđềsaitrongbốnphátbiểusau:

Hàmsốnghịchbiếntrênmỗikhoảng
Trêncáckhoảng

( − ∞;−1) ( 0;1)
và

( − ∞;−1) ( 0;1)
và

.

y' < 0
,

nênhàmsốnghịchbiến.

7

C.
D.

Hàmsốđồngbiếntrênmỗikhoảng
Trêncáckhoảng

( − 1;0) (1;+∞)
và

C©u 41 :

( − ∞;−1) (1;+∞)
và

.

y' > 0
,

nênhàmsốđồngbiến.

3
1 k
2 x 3 + x 2 − 3x − = − 1
2
2 2
có 4 nghiệmphânbiệt.

Xácđịnh k đểphươngtrình

A.

3   19 

k ∈  −2; − ÷∪  ;7 ÷
4  4 


B.

3   19 

k ∈  −2; − ÷∪  ;6 ÷
4  4 


C.

3   19 

k ∈  −5; − ÷∪  ;6 ÷
4  4 


D.

k ∈ ( −3; −1) ∪ ( 1; 2 )

C©u 42 :
Hàmsố

nghịchbiếntrongkhoảng

A. 3

y=
Cho hàmsố
m?
m < −2

y=
Cho hàmsố

mx − 8
x-2m

−2 ≤ m ≤ 2

D.

- 1

. Định m đểhàmsốđạtcựcđạivàcựctiểutạicácđiểmcóhoànhđộlớnhơn

B. m > 2

C©u 44 :

A.

1 3 1 2
x + x + mx
3
2

thì m bằng:

C. 2

B. 1

C©u 43 :

A.

( - 1;1)

y = x3 - 3mx + 5

C. m = 2

D.

m > −2

( 3; +∞ )
, hàmsốđồngbiếntrên
B.

−2 < m < 2

khi:
C.

C©u 45 :

y=

−2 ≤ m ≤

3
2

D.

−2 < m ≤

3
2

x+3
x2 + 1

Tìmtấtcảcácđườngtiệmcậncủađồthịhàmsố
A.
C©u 46 :

y = ±1

B. y = -1

( C)
Từđồthị
củahàmsố
nghiệmthựcphânbiệt.

8

C. x = 1

y = x3 - 3x + 2
. Xácđịnh m đểphươngtrình

D. y = 1

x3 - 3x + 1 = m

có 3

8

A.

0< m< 4

B. 1 < m < 2

C©u 47 :

C. - 1 < m < 3

D. - 1 < m < 7

y = f ( x ) = − x 4 + 18x 2 + 8
Tìmkhoảngđồngbiếncủahàmsốsau:

A.

( −3; 0) U( 3; +∞ )

B.

( −∞; −3) U( −3; 3)

C.

( −∞; −3) U( 0; +∞ )

D.

( −∞; −3) U( 0; 3)

C©u 48 :
Cho hàmsố
A.
B.
C.

1

1
y = − x4 + x2 +
2
2

Hàmsốđạtcựctiểutạiđiểm

x=0

Hàmsốđạtcựctiểutạicácđiểm
Hàmsốđạtcựcđạitạicácđiểm

D.
Hàmsốđạtcựcđạitạiđiểm
C©u 49 :

y=

. Khiđó:

y (0) = 0
, giátrịcựctiểucủahàmsốlà

x = ±1

x = ±1

x=0

.

y (±1) = 1
, giátrịcựctiểucủahàmsốlà

.

y (±1) = 1
, giátrịcựcđạicủahàmsốlà

y (0) =
, giátrịcựcđạicủahàmsốlà

1
2

.

x−2
x+2

Cho hàmsố
có I làgiaođiểmcủahaitiệmcận. Giảsửđiểm M thuộcđồthịsaochotiếptuyếntại M
vuônggócvới IM. Khiđóđiểm M cótọađộlà:
A.

M(0; −1); M(−4;3)

C©u 50 :

B.

M(−1; −2); M(−3;5)

C.

M(0; −1)

D.

M(0;1); M(−4;3)

D.

m Î ( - 1;4)

y = 2x3 + 3( m - 1) x2 + 6( m - 2) x - 1
Cho hàmsố

. Xácđịnh m

( - 2;3)
đểhàmsốcóđiểmcựcđạivàcựctiểunằmtrongkhoảng
A.

9

m Î ( 1;3)

B.

m Î ( 3;4)

C.

m Î ( - 1;3) È ( 3;4)

9

(ĐỀ 002-KSHS)
C©u 1 :
A.

Đồthịhàmsốnàosauđâykhôngcóđiểmuốn
y = x3 − x

B.

C©u 2 :

y = ( x − 1)4

y = x4 − x2

D.

y = ( x − 1)3

C.

T = ( −∞; −10 )

D.

T = ( −10; +∞ )

y = x2 − 6 x − 1
Miền giátrịcủa

A.

C.

T = [ −10; +∞ )

là:
B.

T = ( −∞; −10]

(

C©u 3 :

)

f ( x ) = x3 + 3x 2 − m 2 − 3m + 2 x + 5
Với giá trị m là bao nhiêuthìhàmsố

A. 1 < m < 2

B.

m < 1∨ m > 2

C©u 4 :

A. m < 0

B.

C©u 5 :

5 x3
2m
y=
+ mx −
6
3

m=−

m=

1
2

1
2

m ≤ 1∨ m ≥ 2

hoặc

hoặc

B.

m = −2

D.

y=
Tiếp tuyến của đồ thịhàmsố
x = −2

C.

B.

x+2
x +1

x=2

C©u 7 :

m < 0
m = 1


D.

m > 0
 m = −1


2 
A ,0 ÷
3 
(C). Định m đểtừ
kẻđếnđồ thị hàm số (C) hai tiếp tuyến

m=2

C©u 6 :

A.

D.

vớitrụchoành là 02 khi và chỉ khi

m>0

Cho hàmsố
vuông góc nhau.

C.

C. 1 ≤ m ≤ 2

y = x 4 − 2x 2 + m
Số giao điểm của đồ thịhàmsố

A.

đồngbiếntrên (0; 2)

m=

1
2

m=−

hoặc

1
2

m=2

hoặc

m = −2

tạigiaođiểmvới trục tung cắt trục hoành tại điểm có hoành độ là
C.

x =1

D.

x = −1

f (x ) = − x 4 + 2mx 2 − 1
Tìm m để f(x) có ba cựctrịbiết

10

10

A.

m≤0

B. m > 0

C.

C©u 8 :

m<0

D.

m≥0

f ( x) = mx 4 − ( m + 1) x 2 + m 2 + 2
Với giá trị m là bao nhiêu thìhàmsố

đạtcựctiểu tại

x =1.
A.

m=−

1
3

m = −1

B.

C©u 9 :

C.

m =1

D.

m=

1
3

f (x ) = x 2 − 2x + 8x − 4x 2 − 2
Tìm giá trị lớn nhất của hàmsốsau:

A. 2
C©u 10 :

C. 1

B. - 1

D. 0

y = x 4 − 4 x 3 + 6 x 2 + 1 (C )
Cho

. Mệnh đề nào sau đây đúng?

A. (C) luôn lõm

B.

C. (C) luôn lồi

( 1; 4 )
(C) cóđiểmuốn

D. (C) có 1 khoảng lồi và 2 khoảng lõm

C©u 11 :

y = x3 − 3x 2 + 6
Tìm điểm cực đại của đồ thịhàmsố

A.

x0 = 1

C©u 12 :

x0 = 3

B.

y=

C.

x0 = 2

2x + 6
x+4

D.

M ( 0,1)

Cho hàmsố
cóđồthị (C). Phương trình đườngthẳng qua
sao cho độ dài AB là ngắn nhất. Hãy tìm độ dài AB.
A. 2

B. 3

C©u 13 :
Giá trị lớn nhất củahàmsố

C©u 14 :

trênđoạn

B. 8

C.

D. 5

là
D.

9

12

2

cóhaicực trị là A và B. Khi đó diện tích tam giác OAB là :
B.

4

C©u 15 :

C.

f ( x) =
Đường thẳng qua hai cực trị củahàmsố

11

[ − 4;1]

cắtđồthị hàm số tại A và B

y = x 3 − 3x 2 + 4
Cho hàmsố

A.

C. 4

y = x 2 +6x

A. 7

x0 = 0

2 5

x 2 − 3x + 1
2− x

D. 8

song songvới:
11

A.

y = −2 x + 3

y=

B.

1
x+2
2

C©u 16 :

y = −2 x − 2

C.

1
1
x−
2
2

D.

y=

D.

m≥0

f ( x ) = − x 4 + mx 2 − 1
Tìm m để f(x) có một cựctrịbiết

A.

m<0

m≤0

B.

C©u 17 :

C. m > 0

x 2 + ( 2 − a ) x − 1 + a > 0 ∀x < 1
Với giá trị a baonhiêuthì

.

A. Không tồn tại a thỏa mãn điều kiện trên

C.

a ≥ 4−2 2

C©u 18 :

y= x
Đạo hàm củahàmsố

A.

B. a tùy ý.

0

tạiđiểm

x =0

D.

a > 4−2 2

C.

−1

là

B. Không tồn tại

C©u 19 :
Đồ thị f(x) có bao nhiêu điểm có tọa độ là cặpsốnguyên
A. 3

y=
Cho hàmsố

A.

m > −2

C©u 21 :

2x + m
(C)
x −1
B.

y = x + 1(d)
vàđườngthẳng

. Đường thẳng d cắt đồ thị (C) khi:

m ≥ −2

C.

m>2

M ( −1;3)

B.

M ( 1;3)

m > −2; m = −1

C.

M ( 2;9 )

D.

M ( −2; −3)

C.

( −1; 4 )

D.

( 1; 4 )

f ( x) = x 3 − 3x + 2
Điểm cực đạicủahàmsố

( −1; 0 )

B.

là:

( 1; 0 )

C©u 23 :

[ 0; π ]

f ( x) = sin 3 x − 3sin x + 1
Gọi M, m lần lượt là GTLN và GTNN củahàmsố

12

D.

. Tiếp tuyến tại N(1; 3) cắt (C) tại điểm thứ 2 là M (M ≠ N). Tọa độ M

C©u 22 :

A.

D. Vô số

y = x3 − x + 3
Cho đồthị (C):
là:

A.

1

x2 − x + 2
f (x ) =
x+1

C. Không có

B. 6

C©u 20 :

D.

trên

. Khi đó
12

giá trị M và m là:
A.

M = 3, m = −2

C©u 24 :

y=
Hàmsố

A.

m 3
x + x 2 + x + 2017
3

m < 1

m ≠ 0

C©u 25 :

M = 3, m = 1

B.

m <1

B.

C.

y = − x3 + 3mx 2 − 2 (Cm ), (Cm )

C©u 26 :

M = 1, m = −3

m ≤1

D.

m ≤ 1

m ≠ 0

D.

Các kết quả a, b, c
đều sai

làmtâm đối xứng khi:

m = −1

B.

D.

I (1; 0)
nhận

m =1

M = 1, m = −2

cócựctrịkhi và chỉ khi

Cho
A.

C.

C.

m=0

y = x4 − 4 x2 + 3
Cho hàmsố

cóđồthị (C). Tìm điểm A trên đồ thị hàm số sao cho tiếp tuyến tại A cắt

x A2 + xB2 + xC2 ≥ 8
đồ thị tại hai điểm B, C (khác A) thỏa
A.

A ( −1, 0 )

B.

A ( 1, 0 )

A ( 2,3)

C.

x = kπ ( k ∈ Z)

Tất cả các điểm cực đại củahàmsố

x = π + k 2π ( k ∈ Z)

B.

x = k 2π ( k ∈ Z)

M = 11, m = 2

C©u 29 :

B.

M = 3, m = 2

trên
C.

M = 5, m = 2

D.

M = 11, m = 3

A. m > 0

B. −6 < m < −4

C©u 30 :

π

+ kπ (k ∈ Z)
2

:

y = mx + 3

y = x3 − 3x + 2
Cho hàmsố
cóđồthị (C). Tìm m biết đườngthẳng (d):
phân biệt có tung độ lớn hơn 3.
C.

−6 < m < −

9
2

cắtđồthịtại hai điểm

D.

−

9
< m < −4
2

y = x + 4 − x2
Giá trị nhỏ nhất củahàmsố

13

D.

x=

[ 0; 2]

y = x4 − 2x2 + 3
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của

A.

A ( 0,3)

là

C©u 28 :

A.

D.

y = cos x

C©u 27 :

A.

C.

−2 2

B. 2

là
C. -2

D.

2 2
13

C©u 31 :

y=
Viết phương trình tiếp tuyến d với đồthị (C):

A.

x 7
y = − x − 1, y = − +
4 2

C.

y = x + 1, y =

C©u 32 :

y=
Hàmsố

A.

x 7
−
4 2

x −1
x−m

nghịchbiếntrênkhoảng
B.

C©u 33 :

y=
Cho các đồ thịhàmsố

m>2

m=2

B.

D.

m ∈ ( −∞, −5 )

m≥3

C©u 37 :

y=
Cho

m ≤1

m >1

D. 4

m = 0; m = 1

C.

m =1

D.

y = x 4 − 2 ( m − 1) x 2 + m − 2

Cho hàmsố:
R.

x =1

khi:

m = 0; m = 2

( 1,3)
. Tìm m để hàm số đồngbiếntrên

B.

m ∈ ( 2, +∞ )

1
f ( x) = x3 + 2 x 2 + ( m + 1) x + 5
3

B.

m ∈ [ −5, 2 )

D.

m ∈ ( −∞, 2 ]

. Với m là bao nhiêu thì hàm số đã cho đồng biến trên

m≤3

x 2 − ( m + 1) x + 2m − 1
.
x−m

B.

C.

C.

m<3

D.

m>3

D.

m ≥1

Đểytăng trên từng khoảng xác định thì:

m >1

C©u 38 :

C.

m <1

y = x3 − 6 x + 2
Có bao nhiêu tiếp tuyến của đồ thị hàmsố (C):

14

m≥2

. Hàm số đạt cực trị tại điểm cóhoànhđộ

C©u 36 :

A.

C.

C. 2

Cho hàmsố

A.

D.

x 5
y = − x + 1, y = − +
4 2

y = x 3 − 3(m + 1)x 2 + 3(m − 1) 2 x

C©u 35 :

A.

B.

x 7
y = x − 1, y = − −
2 2

2x − 1
1
y=
x −1
x y = 2x-1 y = 2
,
,
,
. Số đồ thị có tiệm cận ngang là

Hàmsố
A.

biết d đi qua điểm

khivàchỉkhi

B. 3

C©u 34 :

A(−6,5)

(−∞;2)

m ≥1

A. 1

x+2
,
x−2

qua
14

M(1; -3).
A. 2.

B. 3.

C©u 39 :

y=
Cho hàmsố
ngắn nhất.

2x − 7
x−2

A.

C©u 40 :

B.

 13 
M 1  −3, ÷
5

M 2 ( −1,3)

x = 1; x = 0; x = 2

B.

x = 1; x = 0

C.

D.

M 2 ( −1,3)

x =1

D.

Hàm số không có
cực trị

. Tìm m để đồ thị hàm số có cực đại và cực tiểu.

m ∈ ( −1, +∞ )

Cho y =

B.

x2 + x − 3
.
x+2

5

m ∈  −1, ÷
4


m ∈ ( −∞, −1)

D.

5
m ∈ ( −∞, −1) ∪  , +∞
4

B. y có một cực trị

C. y có hai cực trị
C©u 43 :

C.

Cácmệnhđề sau đây, mệnh đề nào đúng?

A. y không có cực trị

D.

ytăngtrên

¡

y = ax 3 + bx 2 + cx + d
Hàmsố

đồngbiếntrên R khi:

A.

a = b = 0, c > 0

2
a > 0; b − 3ac ≤ 0

C.

a = b = 0, c > 0
 2
 b − 3ac ≤ 0

C©u 44 :

y=
Cho hàmsố
Ox.

15

M 2 ( 3, −1)

y = − x 3 + (2m − 1) x 2 − ( 2 − m ) x − 2
Cho hàmsố

C©u 42 :

C.

M 1 ( 3, −1)

đạtcựctrị tại điểm có hoành độ là:

C©u 41 :

A.

M 1 ( 1,5 )

y = 3 (x 2 − 2x)2
Hàmsố

A.

D. 0.

cóđồthị (C). Tìm điểm M trên (C) sao cho khoảng cách từ M đến gốc tọa độ là

M 1 ( 3, −1)
 1
M 2  4, ÷
 2

C. 1.

mx3
− 5 x 2 + mx + 9
3

B.

a = b = 0, c > 0

2
a > 0; b − 3ac ≥ 0

D.

a = b = c = 0

2
a > 0; b − 3ac < 0

cóđồthịhàm số là (C). Xác định m để (C) có điểm cực trị nằm trên

15

A.

m=3

B.

m = ±2

C©u 45 :

C.

m = −2

D.

m = ±3

f (x ) = 2x − x 2 + 4x − 2x 2 − 2
Tìm giá trị nhỏ nhất của hàmsốsau:

A. 0

C. Không có

B. -2

C©u 46 :

y=
Cho

−3x + 6
(C )
x−2

. Kết luận nào sau đây đúng?

A. (C) không có tiệm cận

C.

(C) có tiệmcậnđứng

C©u 47 :

y=
Cho hàmsố
B thỏamãn

A.

2x + 1
x −1

C.

B.

f ( x) =

.

Hàm sốnghịchbiếntrên

−

.

x3 − x 2 − x + m = 0

5
≤ m ≤1
27

M(2;5); M(−2;1)

D.

M(0; −1); M(1; 2)

x +1
x −1

B.

−

B.
D.

¡ \{1}
Hàm số nghịchbiếntrên

.

¡ \{1}
Hàm số đồngbiếntrên

.

[ − 1;1]
cóhainghiệmphânbiệtthuộc

5
< m ≤1
27

C.

−

khi:

5
< m <1

27

D.

−1 ≤ m <

5
27

y = x3 − 3x + 2
Cho hàmsố
saocho

16

C.

(−∞;1), (1; +∞)

C©u 50 :

A.

M(0; −1)

(−∞;1) U (1; +∞)

Phươngtrình
A.

D. (C) là một đường thẳng

Hàm số đồngbiếntrên

C©u 49 :

(C) có tiệmcậnngang

. Khi đó điểm M có tọa độ là:

Cho hàmsốsau:
A.

y = −3

. Tiếp tuyến tại điểm M thuộc đồ thị cắt Ox và Oy lần lượt tại hai điểm A và

OB = 3OA

C©u 48 :

B.

x=2

M(0; −1); M(2;5)

D. 2

cóđồthị (C). Tìm trên đồ thị hàm số (C) điểm M cắt trục Ox, Oy tại A, B

uuur uuur
MA = 3MB

M ( 1, 0 )

B.

M ( 0, 2 )

C.

M ( −1, 4 )

D. Không có điểm M.

16

17

17

(ĐỀ 003-KSHS)
C©u 1 :

y=
Hàm số

A.

2sin x − 1
sin x + 2

−3

có GTLN là

B.

−1

C. 1

C©u 2 :
Với giá trị nào của m thì phường trình

A.

m = −3

m ∈ (−4; −3)

C©u 3 :

B.

x4 − 2x2 = m + 3

hoặc

C.

m = −4

 4
A. 0; 3 

B.

Tìm m để hàm số:

B.
y=

18

;
C.

4

 3 ; +∞ ÷

m ≤ −2

x- 1
x +2

Cho hàm số

D.

D.

m ∈ (−∞; −4)

( −∞;0 )

C.

nghịch biến trên

m > −2

D.

 4
 0; ÷
 3

¡
m ≥ −2

(H)

có đồ thị là
(H)

Tiếp tuyến với

D.

4

 ; +∞ ÷
3


x3
y = ( m + 2) − ( m + 2) x 2 + ( m − 8) x + m 2 − 1
3

m < −2

C©u 5 :

C.

m ∈ (−3; +∞)

;

C©u 4 :

B.

có 4 nghiệm phân biệt (m là tham số).

đồng biến trên khoảng nào?

( −∞;0]

A.

1
3

y = −2 x3 + 4 x 2 + 5
Hàm số

A.

D.

. Chọn đáp án sai.
(H )

tại giao điểm của
(H )

Có hai tiếp tuyến của

với trục hoành có phương trình :

1
y = ( x - 1)
3

I (- 2;1)

đi qua điểm

(H)

Đường cong

có vô số cặp điểm mà tiếp tuyến tại các cặp điểm đó song song với nhau
(H)

Không có tiếp tuyến của

I (- 2;1)

đi qua điểm

18

C©u 6 :

y = 3x + 10 − x 2
Giá trị nhỏ nhất của hàm số

A.

−3 10

B.

C©u 7 :
Cho hàm số
A.
C©u 8 :

B.

C. 10

3 10

x 2 + mx + 1
y=
x+m

m = −1 ∨ m = −3

là:

. Định mđể hàm số đạt cực trị tại

m = −1

x=2

m < −2

C.

y = 2x3 - 3( 2a +1) x2 + 6a( a+1) x + 2
Cho hàm số

D. Không xác định.

D.

m = −3

x1, x2
. Nếu gọi

lần lượt là hoành độ các điểm

x2 - x1
cực trị của hàm số thì giá trị
A.
C©u 9 :

a- 1.

B.

là:

a.

C. 1.

D.

a+1.

Trong các hàm số sau, hàm số nào đơn điệu trên tập xác định của chúng.

A.

f (x) =

2x −1
x +1

B.

f '( x) = 4 x 3 − 2 x 2 − 8 x + 2

C.

f ( x) = 2 x 4 − 4 x 2 + 1

D.

f (x) = x 4 + 2 x 2

C©u 10 :

y = x3 −
Cho hàm số:

9 2 15

13
x + x+
4
4
4

, phát biểu nào sau đây là đúng:

A. Đồ thị hàm số có tiệm cận ngang và tiệm cận

B. Đồ thị hàm số cắt trục hoành tại 1 điểm.

đứng.
C. Hàm số có cực trị.
C©u 11 :

D. Hàm số nghịch biến trên tập xác định.

y = ( m − 3) − 2mx 2 + 3
3

Với giá trị nào của tham số m thì hàm số
A.

m=3

B. Không có m thỏa yêu cầu bài toán.

C.

m = 3∨ m = 0

D.

C©u 12 :

19

không có cực trị

m=0

Tìm m để hàm số sau giảm tên từng khoảng xác định

19

A.

−2 ≤ m ≤

−1
2

C©u 13 :

B.

m < −2

m>2

1
2

D.

m

B.

m≥2

.

y=

có tiệm cận đứng là

2
3

3
x
=
C.
2

. Giá trị

m =1

m

C.

(C )

m¹ 1

D.
(C )

Cho đường cong
có phương trình
cong có phương trình nào sau đây ?

. Tịnh tiến

y = 1 - x2 + 2

C.

y = - x2 + 4x - 3

2
x
=
D.

3

để hàm số đồng biến trên

y = 1- x2

B.

∀m ∈ R

D.

( C)

1
y = x 3 - mx 2 + (2m - 1)x - m + 2
3

C©u 16 :

C©u 17 :

m<

, m là tham số. Hàm số nghịch biến trong

7 x2 + 4x + 5
( C) : y =
2 − 3x

C©u 15 :

A.

C.

y = x 3 − 3mx 2 + 3(m 2 − 1) x − 2m + 3
Cho hàm số
khoảng(1;2) khi m bằng:

A.

1
2

sang phải

y = 1 - x2 - 2

2

¡

là :
m <1

đơn vị, ta được đường

D.

y = - x2 + 4x + 3

Hàm số nào sau đây nghịch biến trên các khoảng xác định của nó:

y=

x−2
x+2

B.

y=

2− x
2+ x

C.

y=

2+ x
2− x

C©u 18 :

D.

Không có đáp án
nào đúng.

y = −2 x3 + 3x 2
Viết phương trình đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số

A.

y = −x

C©u 19 :

B.

y = x +1

m =1

y = x −1

D.

y=x

x = −1

y = x 4 − 2m 2 x 2 + 5

Tìm m để hàm số
A.

C.

đạt cực tiểu tại
B.

m = ±1

C©u 20 :

C.

m = −1

D.

m∈∅

y = − x 4 − 2x 2 + 3
Tìm khoảng đồng biến của hàm số

20

20

A. (-1;0)

( 0; +∞ )

B.

C©u 21 :

C. (0;1)

D.

( −∞;0 )

2x + 3
x +1

Cho hàm số
có đồ thị (C). Điểm M thuộc (C) thì tiếp tuyến của đồ thị (C) tại M vuông góc
với đường y= 4x+7. Tất cả điểm M có tọa độ thỏa mãn điều kiện trên là:
A.

C.

 5
M 1; ÷
 2

hoặc

3

M  −3; ÷
2


3

.

y = x3 + 3mx 2 + (3m2 + m + 1) x + 5m

Tìm m để hàm số đồng biến trên tập xách định
A.

m>1

C.

B. m<1

C©u 23 :

D.

m>

1
2

C©u 24 :

có đúng 1 cực trị:
B.

m≤

1

2

C.

m<

1
2

D.

m≥

1
2

y = 3x 2 − 2 x3
Hàm số

đạt cực trị tại

A.

xCÐ = 0; xCT = 1

B.

xCÐ = 0; xCT = −1

C.

xCÐ = −1; xCT = 0

D.

xCÐ = 1; xCT = 0

C©u 25 :
Với những giá trị nào của
A.

m ≥ −1

y = − x 4 + 2(2m − 1) x 2 + 3
Tìm m để hàm số:

A.

m ≤ −1

m = 1; m = 2

C©u 26 :

B.

y=
Cho hàm số

mx − 1

x+2

m

y=

(C )

thì đồ thị

m = 0; m = 1

của hàm số
C.

x2 - 2x + m
x- m

m=0

không có tiệm cận đứng ?
D.

m = 0; m = 2

y = 2 x −1
có đồ thị Cm (m là tham số). Với giá trị nào của m thì đường thẳng
10

cắt đồ thị Cm tại 2 điểm phân biệt A, B sao cho AB=

giá trị của
A.
C©u 29 :
A.

cắt trục tung tại điểm

( 2016;- 2016) .

M ( 2016;0) .

B.
x 2 - ax + b
x- 1

A + 2B

m=−

C.

M

6

. Đặt

. Để hàm số đạt cực đại tại điểm

1

B.

thì tổng

3

C.

D.

0

Hàm số nào sau đây nghịch biến trên toàn trục số ?
y =- x3 + 3x2 - 3x + 1

y = x3 - 3x2 - 1

B.

y =- x 3 + 3 x - 2

C.

D.

y = x3 + 3

y = x3 − 2x 2 + x − 12
với trục Ox là:

C.

B. 1

C©u 31 :

y = g(x) =Cho hàm số
8
3

B.

C©u 32 :

y=
Hàm số

x4
− 2x 2 − 1
2

x = 2; y = −3

B.

1
+ ln( tan x)
2sin2 x
12
3

C.

16
3

D.

32
3

C.

x = ± 2; y = −3

D.

x = − 2; y = −3

đạt cực đại tại:

x = 0; y = −1

Dùng định nghĩa, tính đạo hàm của hàm số sau:

y' =

2 x 2 − 3x + 4
y=
x2 + 1

M ( 0;0) .

là :

A. 0

A.

D.

A(0; - 1)

Số điểm chung của đồ thị hàm số

A.

m≠

có tọa độ ?

M ( 0;- 2016) .

C.

−1
2

D.

A. Có tiệm cận đứng.

B. Có tiệm cận đứng và tiệm cận xiên.

C. Không có tiệm cận.

D. Có tiệm cận ngang.

C©u 35 :

A.
B.
C.
D.

y =-

[- 1;1]
Trên đoạn

, hàm số

- 1

Có giá trị nhỏ nhất tại

4 3
x - 2x2 - x - 3
3

và giá trị lớn nhất tại

1

Có giá trị nhỏ nhất tại

và giá trị lớn nhất tại

- 1

Có giá trị nhỏ nhất tại

Đường thẳng

y=
cắt đồ thị hàm số

A. (0;-1) và (2;1)
C©u 37 :

C.

D.

2
x

tại các điểm có tọa độ là:

C. (0;2)

D. (1;2)

. Khẳng định nào sau đây sai

Đạo hàm của hàm số đổi dấu khi đi qua
Hàm số có giá trị cực tiểu là
Hàm số có GTNN là

- 1
.

2x −1
x +1

B. (-1;0) và (2;1)

y =- x Cho hàm số

B.

1
.

và không có giá trị lớn nhất.

y = x −1

A.

1
.

Không có giá trị nhỏ nhất và có giá trị lớn nhất tại

C©u 36 :

- 2 2

2 2

x =-

2

và

, giá trị cực đại là

, GTLN là

x = 2.

- 2 2

.

2 2.

(-

)

)

2;- 2 2 .

và điểm cực đại là

y=
Phương trình đường thẳng vuông góc với

(

2;2 2

Đồ thị của hàm số có điểm cực tiểu là

C©u 38 :

23

y' =

x
+1
9

y = − x 3 + 3x 2 + 1
và tiếp xúc với (C):

m ≤1

C.

x =1

D.

y =3

C.

sin( tan x) .

C.

.

có tiệm cận ngang là

x=3

y = cos( tan x)
Đạo hàm của hàm số

sin( tan x) .

y=
Tìm m để hàm số

A. m > ± 2
C©u 43 :

bằng:
B.

C©u 42 :

B.

y=

sin( tan x) .

mx − 2
m− x

m > 2

 m < − 2

C.

( C)
có đồ thị là

m ≥ 2

 m ≤ − 2

C©u 44 :

a = 1; b = 2.

. Tại điểm

a = 2; b = 1.

a

và

( C)
, tiếp tuyến của

b

song

là:

a = 3; b = 1.

D.

a = 1; b = 3.

Trong các hàm số sau, hàm số nào đồng biến trên R.

A.

f ( x) = 3x 3 − x 2 + x

C.

f ( x) =

x −1
3x − 2

C©u 45 :

B.

f ( x) = 2 x 3 − 3 x 2 + 1

D.

f ( x) = x 4 + 4 x 2 − 1

y=
Tiệm cận đứng và tiệm cận ngang của hàm số

24

C.

m∈¡

( C)
thuộc

. Các giá trị thích hợp của
B.

1
D. - sin( tan x) . cos2 x

D.

M ( - 2;- 4)

7x - y + 5 = 0
song với đường thẳng

1
.
cos2 x

đồng biến trên các khoảng xác định:

ax + 2
bx + 3

Cho hàm số

A.

y = 9x + 4

( C)
B.

C©u 41 :

A.

D.

, m là tham số. Hàm số đạt cực tiểu tại x =2 khi m bằng:

m =1

C©u 40 :

A.

y = 9x+14; y = 9x-26

y = x3 − 3mx 2 + (m 2 − 1) x + 2
Cho hàm số

A.

C.

2x − 1
x+2
là:

24

A.

x = 2; y = −2

C©u 46 :

B.

x = −2; y = 2

C.

x = −2; y = −2

x = 2; y = 2

( d ) : y = mx − 2m − 4

( C ) : y = x3 − 6x 2 + 9x − 6
Cho hàm số

D.

. Định m để đường thẳng

cắt đồ thị

( C)
tại ba điểm phân biệt.
A.

m<3

C©u 47 :

B.

y=

m < −3

m > −3

m

nghịch biến trên từng khoảng xác định thì giá trị của
B.

m¹ 2.

C. - 1< m< 2.

D.

m> 2.

. Hãy chọn hệ thức đúng:

A.

y'.cos x - y.sin x - y'' = 0

B.

y'.sin x - y''.cos x + y' = 0

C.

y'.sin x + y.cos x + y'' = 0

D.

y'.cos x + y.sin x + y'' = 0

C©u 49 :

y = x 3 − 3x 2 + 2
Tiếp tuyến của đồ thị hàm số

A.

y = 9x + 7

C©u 50 :

B.

tại điềm M(-1;-2) là

y = 9x − 2

C.

y = 24 x − 2

y = x3 - 3x2 - 9 x + 4

Cho hàm số
A.

là:

y = ecosx
Cho hàm số

25

D.

2x + m

m< 2.

C©u 48 :

m>3

( m- 1) x +1

Nếu hàm số
A.

C.

- 207

. Nếu hàm số đạt cực đại
B.

- 302

C.

x1

- 82

và cực tiểu

y = 24 x + 22

D.
x2

thì tích
D.

y( x1 ).y( x2 )

bằng :

25

25

350 câu trắc nghiệm chuyên đề hàm số ôn thi thpt quốc gia (file Word có đáp án)

Tài liệu liên quan

Tài liệu bạn tìm kiếm đã sẵn sàng tải về