Nghiên cứu ổn định flutter của mô hình mặt cắt dầm cầu 2D. Từ đó, nghiên cứu điều khiển thụ động ổn định flutter của dầm chủ cầu treo
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (762.04 KB, 24 trang )
MỞ ĐẦU
Cơ sở khoa học
Sau sự sụp đổ toàn bộ của cầu Tacoma Narow tại Mỹ vào năm
1940 do mất ổn định flutter, hiện tượng khí động học đã được tập
trung nghiên cứu nhiều trong lĩnh vực xây dựng cầu. Đặc biệt, mất
ổn định flutter được quan tâm nghiên cứu đối với các cầu đàn hồi
nhịp lớn. Trong những năm gần đây, một số lượng lớn các cầu dây
(dây văng và dây võng) đã và đang được xây dựng tại Việt Nam.
Việt Nam là một đất nước chịu ảnh hưởng nhiều của gió và bão. Do
đó, rất cần thiết phải nghiên cứu mất ổn định flutter của cầu nhịp lớn.
1. Mục đích nghiên cứu của luận án
Trong luận án cố gắng giải quyết ba vấn đề cơ bản sau đây:
- Phát triển phương pháp tính vận tốc gió flutter tới hạn của cầu trên
cơ sở mô hình dao động uốn xoắn của dầm chủ.
- Xây dựng một số phần mềm chuyên dụng tính toán vận tốc gió tới
hạn phục vụ cho việc kiểm định thiết kế và duy tu bảo dưỡng cầu
treo.
- Điều khiển thụ động vận tốc flutter của cầu treo bằng phương pháp
cơ học và phương pháp khí động học
2. Đối tƣợng và phạm vi nghiên cứu
Đối tượng nghiên cứu của luận án
Nghiên cứu ổn định flutter của mô hình mặt cắt dầm cầu 2D. Từ
đó, nghiên cứu điều khiển thụ động ổn định flutter của dầm chủ cầu
treo.
Phạm vi nghiên cứu của luận án
Luận án trình bày áp dụng của phương pháp bước lặp để tính
toán sự mất ổn định flutter của một số cầu treo có chiều dài nhịp lớn.
Phần quan trọng của luận án trình bày ứng dụng phương pháp bước
lặp để tính toán điều khiển thụ động dao động flutter của dầm chủ
cầu treo bằng phương pháp cơ học (lắp bộ TMD) cũng như bằng
phương pháp khí động học (lắp hai cánh vẫy).
3. Phƣơng pháp nghiên cứu
- Phương pháp mô hình hóa: xây dựng mô hình cơ học và mô hình
tính toán của kết cấu cầu hệ dây.
- Phương pháp mô phỏng số: Phát triển phương pháp bước lặp của
Matsumoto tính toán vận tốc flutter tới hạn của cầu khi có lắp bộ
điều chỉnh rung (cơ học và khí động học) và khi không lắp.
1
- Phương pháp thực nghiệm: Tham gia làm thực nghiệm nghiên cứu
ảnh hưởng của bộ TMD đến vận tốc gió tới hạn của mô hình cầu
trong phòng thí nghiệm trường Đại học Kỹ thuật Hamburg.
4. Những kết quả mới đạt đƣợc
- Phát triển ý tưởng phương pháp bước lặp của M. Matsumoto tính
vận tốc gió tới hạn của mặt cắt cầu 2 bậc tự do [117] sang tính toán
mô hình mặt cắt cầu có lắp bộ điều chỉnh rung 4 bậc tự do.
- Xây dựng 2 chương trình tính toán vận tốc gió tới hạn: FlutterBK01 và Flutter-BK02, dựa trên phần mềm MATLAB để tính toán
vận tốc flutter tới hạn của cầu dưới tác dụng của gió.
- Bước đầu tối ưu các tham số của bộ giảm chấn khối lượng-cản
(TMD) cho dầm chủ cầu hệ dây, từ đó đưa ra những nhận xét,
khuyến nghị việc lắp đặt bộ tắt chấn cơ học sao cho đạt hiệu quả
mong muốn. Kết quả này có thể áp dụng trong những giải pháp giảm
dao động dưới tác dụng của gió của một cầu treo bất kỳ.
- Áp dụng các kết quả nghiên cứu để tính toán cho một mô hình mặt
cắt dầm cầu cụ thể. Các kết quả thu được là hợp lý giữa tính toán lý
thuyết và thực nghiệm.
5. Bố cục của luận án
Luận án gồm năm chương và phần Kết luận, kiến nghị với 126
trang, 56 hình vẽ và đồ thị, 9 bảng biểu.
1 TỔNG QUAN
1.1 Cầu hệ dây và gió
Hiện nay, các kết cấu cầu hệ dây (dây văng và dây võng) được
xây dựng ngày càng nhiều tại Việt Nam với khả năng vượt nhịp lớn
cùng với ưu điểm về mặt kiến trúc mỹ quan. Tuy nhiên, do có dạng
kết cấu thanh mảnh nên các công trình cầu dây văng, dây võng rất
nhạy cảm với tác động của gió bão.
1.2 Mô hình dao động của cầu dây võng và cầu dây văng dƣới
tác dụng của gió
Để nghiên cứu ảnh hưởng của gió đến công trình cầu, đầu tiên ta
phải xây dựng mô hình dao động của cầu dưới tác dụng của gió. Đến
nay người ta xây dụng hai loại mô hình: mô hình mặt cắt và mô hình
toàn cầu [36, 80, 96, 97, 142, 150, 154, 155].
Về mặt cơ học mô hình mặt cắt là mô hình hệ dao động hai bậc
tự do (dao động uốn và dao động xoắn) hoặc mô hình hệ dao động ba
2
bậc tự do (dao động uốn, dao động xoắn, dao động ngang). Do dao
động ngang ít có ảnh hưởng lớn nên người ta thường sử dụng mô
hình hai bậc tự do.
Mô hình toàn cầu còn ít được nghiên cứu [36, 96, 97, 142, 154,
155]. Phương pháp phần tử hữu hạn và phương pháp khai triển theo
các dạng riêng là hai phương pháp thích hợp để xây dụng mô hình và
tính toán dao động toàn cầu.
1.3 Các phƣơng pháp tính vận tốc flutter tới hạn
Để tính toán vận tốc tới hạn flutter của gió, người ta thường sử
dụng các phương pháp sau:
- Phương pháp trị riêng phức
- Phương pháp khái niệm số phức
- Phương pháp sử dụng tiêu chuẩn Routh – Hurwitz
- Phương pháp bước lặp
1.4 Các biện pháp nâng cao vận tốc flutter tới hạn
Có hai phương pháp chính để nâng cao vận tốc fluter tới hạn là
phương pháp cơ học (sử dụng các bộ giảm chấn khối lượng-cản
(TMD)) và phương pháp khí động học (sử dụng các cánh vẫy), đối
với mỗi phương pháp lại có thể sử dụng mô hình điều khiển chủ
động hoặc mô hình điều khiển thụ động.
1.5 Nội dung của luận án
Do tính phức tạp của mô hình bài toán dao động của cầu dưới tác
dụng của gió, trong luận án này chỉ sử dụng mô hình mặt cắt để
nghiên cứu tính toán mất ổn định flutter của cầu. Trong quá trình
nghiên cứu chúng tôi thấy phương pháp bước lặp của GS. M.
Matsumoto (Trường Đại học Kyoto) là một phương pháp mới đề
xuất trong vòng 10 năm gần đây và còn nhiều vấn đề có thể nghiên
cứu phát triển. Vi vậy trong luận án đã nghiên cứu sử dụng và phát
triển phương pháp bước lặp tính toán vận tốc flutter của mô hình cầu.
Trong luận án cũng sử dụng và phát triển phương pháp bước lặp để
nghiên cứu bài toán điều khiển thụ động kết cấu cầu dây sử dụng các
bộ giảm chấn khối lượng-cản (TMD) và sử dụng các cánh vẫy bị
động.
2
NHẬN DẠNG TÁC DỤNG CỦA GIÓ VÀ MÔ HÌNH DAO
ĐỘNG FLUTTER CỦA DẦM CHỦ TRONG KẾT CẤU
CẦU HỆ DÂY
3
2.1 Số liệu gió dùng trong thiết kế
2.1.1 Tốc độ gió cơ bản U10 m/s [29, 34, 132, 133]
Theo tiêu chuẩn về thiết kế kháng gió cho cầu đường bộ tại Nhật
Bản [132, 133], tốc độ gió cơ bản là tốc độ gió trung bình trong vòng
10 phút ở độ cao 10m so với mặt đất hoặc mặt nước, thông thường
lấy theo chu kỳ lặp 100 năm.
2.1.2 Tốc độ gió thiết kế U d m/s [16, 132, 133]
Cũng theo tiêu chuẩn về thiết kế kháng gió cho cầu đường bộ tại
Nhật Bản [132, 133], vận tốc gió thiết kế được tính theo công thức
(2.3)
U d U10 . E1
2.1.3 Đặc tính giật của tốc độ gió [29, 47, 68, 150]
Gió có thể được coi là sự chuyển động nhiễu loạn của không khí.
Chuyển động này có đặc điểm không là không theo quy luật và luôn
thay đổi theo không gian và thời gian.
2.2 Các hiện tƣợng dao động của cầu phát sinh bởi gió
Theo tài liệu [13], phản ứng của công trình dưới tác dụng của gió
là tổng hợp các hiện tượng khí lực học cơ bản.
2.2.1 Tác dụng tĩnh của gió lên cầu
2.2.1.1 Biến dạng và ứng suất tĩnh [13, 47, 68, 150]
Đây là các hiện tượng tĩnh, không phụ thuộc vào thời gian, chúng
được gây ra bởi vận tốc gió trung bình. Lực đẩy, lực nâng và momen
xoắn trên một đơn vị dài được xác định [47, 150]
1
U 2 BCD
2
1
L U 2 BCL
2
1
M U 2 B 2CM
2
D
(2.5)
(2.6)
(2.7)
2.2.1.2 Các hiện tượng mất ổn định tĩnh
a. Mất ổn định uốn ngang [13, 126, 167]
Theo tài liệu [13], xét trường hợp một dầm lăng trụ chịu tác dụng
của momen uốn trong mặt phẳng xz, khi momen uốn này còn trong
một phạm vi nhỏ thì kết cấu sẽ chỉ bị biến dạng trong mặt phẳng
momen uốn tác dụng. Nhưng khi momen uốn đạt tới một giá trị tới
hạn thì sẽ xảy ra hiện tượng mà trong đó chuyển vị uốn theo trục y
4
của dầm và xoắn xung quanh trục vuông góc trọng tâm của dầm liên
hợp với nhau và tăng nhanh một cách đột ngột. Hiện tượng này được
gọi là hiện tượng mất ổn định uốn ngang. Trong trường hợp dầm cầu
treo dây văng, công thức xác định lực phân bố tới hạn [165]
EI z GIT
(2.10)
qcr 28.3
L3
Vận tốc gió tới hạn được suy ra từ công thức (2.5) [125]
1/2
2qcr
U cr
CD B
(2.11)
b Mất ổn định xoắn [47, 68, 150]
Dưới tác dụng của momen xoắn, góc tới cũng sẽ tăng và như
vậy sẽ dẫn tới một momen xoắn lớn hơn. Do momen xoắn tỷ lệ với
bình phương vận tốc gió nên đến một lúc nào đó độ cứng chống xoắn
của kết cấu không đủ chống lại momen xoắn tác dụng. Khi đó kết
cấu sẽ mất ổn định. Vận tốc mất ổn định xoắn
2k
(2.13)
U cr
B 2 C 'M 0
2.2.2 Tác dụng động của gió lên cầu
2.2.2.1 Dao động do xoáy khí (Vortex-induced vibration) [69, 110,
135, 150]
a. Giới thiệu chung - Hiện tượng lock-in1
Trong một số trường hợp, vật cản cố định sẽ chịu tác dụng của
các xoáy khí luân phiên có tần số cơ bản f s , tương ứng với số
Strouhal [150]
fs B
(2.15)
St
U
Khi tần số của các xoáy khí xấp xỉ tần số tần số dao động theo
phương vuông góc hướng gió của vật cản, vật cản sẽ dao động mạnh
hơn và bắt đầu tương tác rất mạnh với luồng gió, quan sát thực
nghiệm chỉ ra rằng tần số xoáy khí bị khống chế trong một phạm vi
tốc độ gió, hiện tượng này gọi là lock-in.
b. Mô hình phân tích hiện tượng dao động gió cuộn xoáy
Theo tài liệu [150], giả thiết rằng hình trụ tròn đặt cố định theo
phương gió thổi cũng như vuông góc với gió thổi. Trong trường hợp
5
này, xấp xỉ lực tác dụng theo phương vuông góc trên mỗi đơn vị
chiều dài của hình trụ là
1
(2.16)
F U 2 BCLS sin s t
2
Mô hình một bậc tự do thường được sử dụng, phương trình có
dạng [69, 110, 150]
m
y 2 1 y 12 y
(2.18)
1
y 2 y
y
2
U B Y1 ( K ) 1 2 Y2 ( K ) CL ( K )sin t
2
B U
B
2.2.2.2 Dao động do gió mưa (Rain-wind-induced vibration) [46,
47, 78, 81, 175, 182]
Trong mục này, nghiên cứu mô hình đơn giản của H. Yamaguchi,
theo các tài liệu [47, 175] nhằm hiểu rõ hơn về nguyên lý mất ổn
định. Hệ phương trình chuyển động có dạng
(2.20)
my ky Fy
I M
(2.21)
2.2.2.3 Dao động do rối của dòng khí (Buffeting) [13]
Trong tài liệu [13], tác giả P. H. Kiên đưa ra một mô hình ví dụ
tính toán đơn giản như sau: Xét một kết cấu với khối lượng tập trung
m , diện tích hứng gió A , hệ số độ cứng và giảm chấn lần lượt là k
và c0 (hình 2.7). Phương trình dao động của kết cấu theo phương gió
thổi (phương x ) có thể viết như sau
(2.22)
mx c0 x kx P x P t
2.2.2.4 Dao động phía cuối gió (Wake-induced vibration) [47]
Theo tài liệu [47], dao động phía cuối gió là một thuật ngữ dùng
để chỉ các hiện tượng dao động của dây cáp nằm trong luồng gió rối
của dây cáp khác hoặc kết cấu khác.
a. Cộng hưởng luồng gió rối
Hiện tượng này có thể xảy ra với cầu có hai mặt phẳng dây cáp
song song. Vận tốc tới hạn U cr được xác định bởi [47]
2B
(2.27)
U cr
Tt
b. Cộng hưởng xoáy khí
6
Vận tốc gió tới hạn U cr để xảy ra hiện tượng cộng hưởng với dây
cáp có tần số f k nằm trong luồng gió cuộn của cột tháp có thể được
xác định [47]
Hf
(2.28)
U cr k
St
c. Hiệu ứng giao thoa
Để hạn chế kích thước của dây cáp, nhiều dây cáp liên hợp bố trí
song song đã được sử dụng đối với một vài cầu dây văng, điển hình
là ở Nhật Bản. [47]
2.2.2.5 Dao động tự kích khí động học theo phương uốn (Galloping)
[47, 68, 150]
Hiện tượng này xảy ra bởi dao động vuông góc với hướng gió,
biên độ dao động phát sinh là rất lớn. Điều kiện cần thiết để mất ổn
định là
dCL
CD 0
d
0
(2.32)
2.2.2.6 Hiện tượng dao động tự kích khí động học uốn xoắn (Flutter)
a. Hệ phương trình dao động tự kích khí động học uốn xoắn của
hệ hai bậc tự do [150]
Hình 2.12 Mô hình dao động flutter
Đây là hiện tượng khí động xảy với các công trình có hai bậc tự
do, di chuyển xoắn và di chuyển uốn cùng xảy ra trong luồng gió
thổi gây ra sự mất ổn định. Phương trình chuyển động (hình 2.12) :
7
(2.33)
mh(t ) ch h(t ) kh h(t ) Lh
(2.34)
I(t ) c (t ) k (t ) M
b. Lực nâng và momen khí động
E. Simiu và R.H. Scalan đã biểu diễn hàm lực gió dưới dạng số
thực [150]
1
h
B
Lh U 2 B KH1* ( K ) KH 2* ( K )
2
U
U
(2.38)
K 2 H 3* ( K ) K 2 H 4* ( K )
M
h
B
1
h
B
U 2 B 2 KA1* ( K ) KA2* ( K )
2
U
U
(2.39)
h
K 2 A3* ( K ) K 2 A4* ( K )
B
với K là tần số thu gọn
c. Mô hình flutter ba bậc tự do
Các thành phần lực khí động có dạng [92, 96, 139, 150]
1
h
B
Lh U 2 B KH1* KH 2*
K 2 H 3*
2
U
U
h
p
p
KH 5* K 2 H 6*
B
U
B
1
h
B
M U 2 B 2 KA1* KA2*
K 2 A3*
2
U
U
(2.40)
K 2 H 4*
h
p
p
KA5* K 2 A6*
B
U
B
1
p
B
Dp U 2 B KP1* KP2*
K 2 P3*
2
U
U
p
h
h
K 2 P4* KP5* K 2 P6*
B
U
B
(2.41)
K 2 A4*
(2.42)
Trong trường hợp dầm cầu có dạng đối xứng điển hình, phương
trình chuyển động của một mặt cắt phẳng của dầm cầu có dạng [149]
(2.43)
mh(t ) ch h(t ) kh h(t ) Lh
8
I(t ) c (t ) k (t ) M
(2.44)
t c p p t k p p t Dp
mp
(2.45)
2.3 Các mô hình lực gió tự kích tác dụng lên dầm cầu
2.3.1 Mô hin
̀ h lƣ̣c theo miền tầ n số
Các lực khí động cho hệ hai bậc tự do và ba bậc tự do được trình
bày như trong mục 2.2.2.6.
2.3.2 Mô hin
[109, 143, 145,
̀ h lƣ̣c tƣ̣ kích theo miền thời gian
176]
Các lực tự kích có thể được biểu diễn theo miền thời gian (tham
khảo tài liệu [143, 145, 176]).
2.3.3 Mô hin
̀ h lƣ̣c gió á bình ổn
Tham khảo các tài liệu [51, 109, 135, 161].
2.4 Một phƣơng án nhận dạng các tham số của mô hình dao
động flutter hai bậc tự do
2.4.1 Thiết lập phƣơng trình dao động uốn xoắn của dầm cầu
Dao động uốn xoắn của dầm có thể được mô tả bởi một hệ hai
phương trình vi phân đạo hàm riêng như sau
2w
w 2
m 2 cbe
t x 2
t
2 w i 3w
EI 2 cb 2 AL
x t
x
(2.95)
cte
ML
GIT
2
t x
x
t
b I P
2
2.4.2 Biến đổi hệ phƣơng trình dao động uốn-xoắn của dầm về
hệ các phƣơng trình vi phân thƣờng
Trong trường hợp mô hình dầm giản đơn, tìm nghiệm hệ phương
trình dao động uốn-xoắn dưới dạng [20]
n
n
j
j (2.98)
w x, t h j t sin
x , x, t j t sin
x
j 1
Biến đổi ta được
L
j 1
L
(2.112)
mh(t ) ch h(t ) k h(t ) AL
(2.113)
I(t ) c (t ) k (t ) M L
2.5 Kết luận chƣơng 2
Trong chương 2 của luận án, trình bày sơ lược một số vấn đề cơ
bản về đặc tính của gió, tác dụng của gió lên công trình, đặc biệt lên
cầu treo. Đồng thời trong chương này cũng giới thiệu một số hiện
9
tượng dao động của cầu phát sinh bởi tác dụng của gió. Đó là dao
động do xoáy khí (vortex-induced vibration), dao động do rối của
dòng khí (buffeting), dao động uốn tự kích (galloping), dao động
uốn-xoắn tự kích (flutter), dao động do gió-mưa (rain-wind-induced
vibration). Trong đó dao động uốn-xoắn tự kích là loại dao động
nguy hiểm nhất. Trong các chương sau chủ yếu đi sâu nghiên cứu
hiện tượng flutter.
TÍNH TOÁN ỔN ĐỊNH FLUTTER CỦA DẦM CHỦ CẦU
TREO THEO MÔ HÌNH MẶT CẮT HAI BẬC TỰ DO
BẰNG PHƢƠNG PHÁP BƢỚC LẶP
3.1 Mô hình dao động mặt cắt của dầm chủ theo lý thuyết
flutter cổ điển
3.1.1 Các giả thiết cơ bản của lý thuyết flutter cổ điển
Khi sử dụng lý thuyết flutter cổ điển xác định vận tốc flutter giới
hạn, ta thừa nhận các giả thiết gần đúng theo tài liệu [154]
3.1.2 Hệ phƣơng trình dao động tự kích khí động học uốn xoắn
hai bậc tự do
Xét mặt cắt của cánh hoặc của dầm cầu chịu tác dụng của luồng
gió thổi đều. Mặt cắt giả thiết có hai bậc tự do: di chuyển uốn và di
chuyển xoắn ký hiệu bởi h và . Phương trình chuyển động có thể
viết [150]
(3.1)
mh(t ) ch h(t ) kh h(t ) Lh
3
(3.2)
I(t ) c (t ) k (t ) M
3.1.3. Lực nâng và momen khí động
Xem các phương trình (2.38), (2.39).
3.1.4 Xác định các tham số flutter
Có hai phương pháp thực nghiệm chính để xác định các tham số
flutter Ai* , H i* i 1,..., 4 : phương pháp dao động tự do [55, 61, 76,
90, 158] và phương pháp dao động cưỡng bức [65, 112]. Mối liên hệ
giữa các tham số flutter được tác giả Scanlan đề xuất trong tài liệu
[144].
U. Starossek [157, 158] đã tiến hành xác định các tham số flutter
cho 9 mặt cắt cầu điển hình (hình 3.2) bằng cả thực nghiệm và mô
phỏng số. L. Thiesemann, trong tài liệu [166], đã xác định các tham
số khí động của 31 dạng mặt cắt khác nhau bằng cả thực nghiệm và
10
mô phỏng số. Với các kết quả đạt được về việc xác định các tham số
flutter Ai* , H i* của GS. Starossek và các cộng sự ở Trường Đại học
Kỹ thuật Hamburg [157, 158, 166], việc tính toán vận tốc gió tới hạn
trở nên đơn giản hơn nhiều so với trước đây.
3.2 Tính toán vận tốc tới hạn flutter cho hệ hai bậc tự do bằ ng
phƣơng pháp bƣớc lặp
3.2.1 Phân tích ổn định hệ phƣơng trình dao động tự kích khí
động học uốn xoắn hai bậc tự do
Đưa hệ phương trình lực gió vào hệ phương trình dao động ta thu
được hệ phương trình
(3.17)
D K q C K q 0
MK q
với q h T ; M K ; D K ; C K là các ma trận vuông cấp 2.
Tìm nghiệm hệ (3.17) dưới dạng: q t qet
(3.18)
Xét các trường hợp nghiệm ta sẽ tìm được điều kiện ổn định
tương ứng.
3.2.2 Thuật toán phƣơng pháp bƣớc lặp
Bước 1: Giả thiết chuyển vị xoắn: 0e F F t sin F t
(3.22)
Bước 2: Chuyể n vi ̣uố n phát sinh bởi cá c ngoa ̣i lự c gây ra bởi
chuyể n vi ̣xoắ n, có dạng dao động cưỡng bức
Bước 3: Tiế p tu ̣c, chuyể n vi ̣xoắ n la ̣i đươ ̣c phát sinh bởi chuyể n vi ̣
uố n, có dạng dao động tự do
Phương trình dao động xoắn đươ ̣c viế t la ̣i dưới da ̣ng chuẩ n
(3.67)
2 F F F2 0
Ta tìm được
F [2 1F2 A3* 1 2F2 { A1* H 2* 1 F2 sin 1
3/2
A1* H 3* 1 F2 sin 2 A4* H 2* 1 F2 (cos 1 F sin 1 )
(3.68)
A4* H 3* (cos 2 F sin 2 )}]1/2
2 F 2
1 A2* 12 { A1* H 2* 1 F2 F sin 1 cos 1
F
A H
F sin 2 cos 2 A
*
1
*
3
*
4
H
*
2
1 sin 1 A H sin 2 }
2
F
11
*
4
*
3
(3.69)
Hệ (3.68) và (3.69) là hệ hai phương trình đại số phi tuyến với 2
ẩn F và F . Giải hệ hai phương trình này bằng phương pháp lặp
Newton-Raphson, ta tìm được F , F .
3.3 Mô hình thí nghiệm mặt cắt dầm cầu tại trƣờng Đại học
Kỹ thuật Hamburg
Mô hình mặt cắt dầm cầu GB được thực hiện trong hầm gió của
Viện Phân tích kết cấu và Công trình thép thuộc Đại học Kỹ thuật
Hamburg, mặt cắt có dạng thu nhỏ của mặt cắt ngang dầm cầu Great
Belt ở Đan Mạch.
Các thông số của mô hình (kỹ sư Axel Seils cung cấp):
m 34,8kg, I 0,71kgm2 , kh 2790 N/m, k 70,8 Nm/rad
ch c 0, B 2b 0, 420m, l 0.79m
Hình 3.5 Hình dáng mặt cắt mô hình thí nghiệm (đơn vị: mm)
Hình 3.6 Mô hình thí nghiệm trong thí nghiệm hầm gió
(cung cấp bởi kỹ sư Axel Seils)
Kết quả vận tốc gió tới hạn của mô hình thực hiện trong hầm gió
của trường Đại học Kỹ thuật Hamburg là 9.8 m/s (35.28km/h).
12
Sử dụng phần mềm Flutter-BK01 ta tìm được vận tốc flutter tới
hạn: U F 9.31m/s; F 9.42 rad/s . Kết quả trên phù hợp tốt với kết
quả thực nghiệm là U F 9.8m/s , sai số là 5%.
3.4 Tính toán vận tốc gió tới hạn mô hình mặt cắt của một vài
cầu cụ thể
3.4.1 Tập hợp các số liệu với mặt cắt GB của tác giả Thiesemann
Bảng 3.4 Kết quả tính toán vận tốc flutter U F (m/s)
1
2
3
4
Kết quả tính bằng CT Flutter21.78
39.6
74.1
19.4
BK01
Kết quả tính lý thuyết [166]
21.5
40.2
73.0
15.5
Kết quả tính thực nghiệm
20.6
41.3
70.2
16.1
[166]
Công thức Selberg
21.90
41.73
73.54
23.16
Sai số giữa kết quả tính toán lý
thuyết trong luận án và trong 1.3%
1.49%
1.5%
25.16%
tài liệu [166]
3.4.2 Cầu Great Belt của Đan Mạch
Sử dụng phần mềm Flutter-BK01, ta tìm được vận tốc gió flutter
tới hạn: U F 40.14 m/s; F 0.978rad/s . Theo tài liệu [147],
U F 39.2 m/s; F 0.995rad/s . Sai số vận tốc gió tới hạn giữa tính
toán lý thuyết trong luận án và theo tài liệu [147] là 2.4%.
3.4.3 Cầu Tacoma Narrows cũ của Mỹ
Sử dụng phần mềm Flutter-BK01, ta tìm được vận tốc gió flutter
tới hạn: U F 23.75m/s; F 0.9671rad/s . Kết quả tính toán lý thuyết
trong tài liệu [154] là U F 23.6 m/s; F 0.97 rad/s . Sai số vận tốc
gió tới hạn tính toán theo lý thuyết trong luận án và theo tài liệu
[154] là 0.64%.
3.4.4 Cầu Jiangyin của Trung Quốc
Sử dụng phần mềm Flutter-BK01, ta tìm được vận tốc gió flutter
tới hạn: U F 72.5m/s; F 1.2711rad/s
Kết quả tính toán lý thuyết trong tài liệu [37], U F 72.5 m / s ;
F 1.28rad/s . Sai số vận tốc gió tới hạn tính toán theo lý thuyết
trong luận án và theo tài liệu [37] là 0%.
13
3.4.5 Cầu Vàm Cống của Việt Nam
Sử dụng phần mềm Flutter-BK01, ta tìm được vận tốc gió flutter
tới hạn: U F 75.5m/s; F 3.1249 rad/s . Kết quả này phù hợp với
kết quả trong tài liệu [57], vận tốc gió tới hạn, U F 48.1m/s . Nhận
thấy f h f F f , kết quả này phù hợp với kết quả tính toán và
thực nghiệm của nhiều công trình khác.
3.5 Kết luận chƣơng 3
Trong chương 3 của luận án đã trình bày các vấn đề sau:
- Trên cơ sở phương pháp bước lặp của M. Matsumoto, đã thiết
lập thuật toán và viết phần mềm Flutter-BK01 để xác định vận tốc
gió tới hạn tác dụng lên cầu trên phần mềm MATLAB.
- Nghiên cứu cách xác định các tham số flutter cho các mặt cắt
cầu phổ biến phục vụ cho phần mềm Flutter-BK01.
- Tính toán chi tiết vận tốc gió tới hạn của mô hình cầu của
Trường Đại học Kỹ thuật Hamburg. Các kết quả tính toán theo phần
mềm Flutter-BK01 phù hợp với kết quả thực nghiệm.
- Sử dụng phần mềm Flutter-BK01 tính toán vận tốc gió tới hạn
của cầu Tacoma Narrows (Mỹ), cầu Jiangyin (Trung Quốc), cầu
Great Belt (Đan Mạch), cầu Vàm Cống (Việt Nam). Kết quả tính
toán theo phần mềm Flutter-BK01 phù hợp với các kết quả đã được
công bố, qua đó khẳng định độ tin cậy của phần mềm Flutter-BK01.
ĐIỀU KHIỂN THỤ ĐỘNG DAO ĐỘNG FLUTTER CỦA
DẦM CHỦ CẦU TREO BẰNG PHƢƠNG PHÁP CƠ HỌC
Trong chương này, việc sử dụng bộ giảm chấn khối lượng-cản
(TMD) để tăng vận tốc gió tới hạn của dầm cầu được tiến hành
nghiên cứu bằng cả lý thuyết và thực nghiệm.
4.1 Thiết lập phƣơng trình chuyển động
Phương trình chuyển động (hình 4.1)
m 2mC h mC
y1 mC
y2 ch h kh h Lh
y1 mC bC
y2 c k M
I 2mC bC2 mC bC
(4.8)
y1 cC y1 kC y1 0
mC h mC bC mC
y2 cC y 2 kC y2 0
mC h mC bC mC
4
14
Hình 4.1 Mô hình tính toán
4.2 Sử dụng phƣơng pháp bƣớc lặp giải hệ phƣơng trình vi phân
chuyển động
t
Bước 1: Giả thiế t chuyể n vi xoắ
̣ n: 0e F F sin F t (4.16)
Bước 2: Thay , , vào ba phương trình còn lại của hệ
phương trình dao động, tìm được sáu đại lượng h0 / 0 , y10 / 0 ,
y20 / 0 ,
h , y1 , y 2 theo hai ẩn số F , F . Với h0 , y10 , y20 là
các biên độ dao động, h , y1 , y 2 là độ lệch pha của các dao
động h, y1 , y2 so với dao động xoắn.
Bước 3: Viết lại phương trình dao động xoắn dưới dạng chuẩn
(4.63)
2 F F F2 0
Ta tìm được
15
y01
F mC bC
mC bC
B3
2
B4
y02
0
F F2 1 sin y 2 2 F cos y 2 c
h0
F A1*
0
2
B3
2
B3
2
F A4*
h0
0
sin h
B3
F sin h cos h
(4.64)
F A2* / I 2mC bC2 2F
F2 mC bC
F F2 1 sin y1 2 F cos y1
2
mC bC
0
y02
0
F A1*
F2 A4*
y01
0
2
F
2
F
1 F2 cos y1 F sin y1
1 F2 cos y 2 F sin y 2 k
h0
F sin h 1 F2
h0
cos h sin h F
0
0
B4
2
(4.65)
F2 A3* / I 2mC bC2
Từ hai phương trình (4.64), (4.65) ta có hệ hai phương trình phi
tuyến với F , F .
4.3 Nâng cao vận tốc gió flutter tới hạn của mô hình thí nghiệm
tại trƣờng Đại học kỹ thuật Hamburg
Mô hình mặt cắt dầm cầu được thực hiện trong hầm gió của Viện
Phân tích kết cấu và Công trình thép thuộc Đại học Kỹ thuật
Hamburg, mặt cắt có dạng thu nhỏ của mặt cắt ngang dầm cầu Great
Belt.
Các thông số của TMD (kỹ sư Axel Seils cung cấp):
mC* 0, 058;0,116;0,174kg; kC* 7N/m; cC* 0.081Ns/m;
bC 0, 05;0,10;0,15;0, 20m
16
Hình 4.4 Mô hình thí nghiệm với TMD trong thí nghiệm hầm gió
(cung cấp bởi kỹ sư Axel Seils)
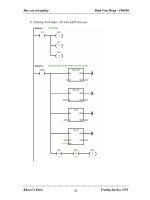
traverse
bridge girder
end plates
damper pot
TMD
Hình 4.5 Bố trí chung của thí nghiệm mặt cắt dầm cầu với TMD
(cung cấp bởi kỹ sư Axel Seils)
17
Bảng 4.1 Bảng so sánh kết quả lý thuyết và thực nghiệm U F m / s
kC = 2*7 N/m, cC = 2*0.081 Ns/m),
mC = 2*0.058; 2*0.116; 2*0.174 kg
mC kg
bC m
0.05
0.1
0.15
0.2
Lý thuyết
9.84
9.8
9.71
9.54
2*0.058
Thực nghiệm
9.9
9.85
9.8
9.9
Lý thuyết
8.96
9.42
10.07
10.87
2*0.116
Thực nghiệm
9.4
9.8
10.2
10.7
Lý thuyết
9.04
9.26
9.62
10.07
2*0.174
Thực nghiệm
9.6
9.7
9.9
10
Nhận thấy kết quả lý thuyết phù hợp tốt với kết quả thí nghiệm,
sai số lớn nhất là 5.83% trong 12 bộ số liệu.
4.4 Nâng cao vận tốc gió flutter tới hạn của cầu Great Belt của
Đan Mạch
Khi chưa lắp TMD, vận tốc gió flutter tới hạn là 40.14 m/s (144.5
km/h).
Trong tài liệu [147], đưa ra phương án lắp TMD với các thông số
như sau:
bC 12.4m, mC 142.4kg, cC 18.1663Ns/m, kC 108.5311N/m
Sử dụng phần mềm Flutter-BK02(a), ta tìm được vận tốc gió tới
hạn
U F 50.7m/s; F 0.89rad/s
Kết quả tính toán lý thuyết trong tài liệu [147]:
U F 49.5m/s; F 0.86Hz . Sai số vận tốc gió tới hạn tính toán
theo lý thuyết trong luận án và trong tài liệu [147] là 2.42%.
4.5 Tính toán tối ƣu các tham số của bộ giảm chấn TMD
Sử dụng phương pháp tìm trực tiếp (Direct Search)
4.5.1 Trƣờng hợp mô hình thí nghiệm tại Trƣờng Đại học Kỹ
thuật Hamburg
Thay đổi các giá trị bC , mC , cC , kC như sau:
bC min 0,05m; bC max 0, 2m; bC 0,05m
18
mC min 0,116kg; mC max 9*0,116kg; mC 0,116kg
kC min 2*4N/m; kC max 2*10N/m; kC 2*1N/m
cC min 0,081Ns/m; cC max 4*0,081Ns/m; cC 0,081Ns/m
Tìm được: bCopt 0, 2m; mCopt 0,116kg; cCopt 2*0,081Ns/m;
kCopt 2*5N/m;U F opt 16.1m/s
Hiệu suất:
U U F 16,1 9,31
Fopt
*100 72,93%
UF
9,31
4.5.2 Trƣờng hợp cầu Great Belt của Đan Mạch
Thay đổi các giá trị bC , mC , cC , kC như sau:
bC min 3, 4m; bC max 12, 4m; bC 1m
mC min 50kg/m; mC max 200kg/m; mC 10kg/m
kC min 50N/m/m; kC max 150N/m/m; kC 10N/m/m
cC min 2Ns/m/m; cC max 20Ns/m/m; cC 2Ns/m/m
Tìm được: bC opt 11, 4 m ; mC opt 90 kg/m ; cC opt 4Ns/m/m ;
kC opt 80N/m/m; U F opt 73.9m/s
Hiệu suất:
U UF
73,9 40,14
Fopt
*100 84,11%
%
U
40,14
F
4.5 Kết luận chƣơng 4
Trong chương 4 của luận án đã giải quyết các vấn đề sau:
- Mở rộng phương pháp bước lặp của M. Matsumoto và các đồng
nghiệp từ hệ 2 bậc tự do [117] sang hệ 4 bậc tự do. Trên cơ sở các
công thức thu được, xây dựng phần mềm Flutter-BK02(a), tính toán
vận tốc gió tới hạn của dầm chủ khi lắp thêm các bộ TMD.
- Tính toán vận tốc gió tới hạn cho dầm của cầu khi lắp TMD
trong 2 trường hợp: mô hình cầu của trường Đại học Kỹ thuật
Hamburg, mô hình cầu Great Belt của Đan Mạch. Hiệu quả của việc
lắp đặt bộ TMD là nâng cao vận tốc gió tới hạn lên khoảng 70-80%.
- Tham gia nhóm nghiên cứu của GS. Nguyễn Văn Khang tiến
hành làm thí nghiệm nghiên cứu ảnh hưởng của bộ TMD đến vận tốc
19
gió tới hạn của mô hình cầu trong phòng thí nghiệm trường Đại học
Kỹ thuật Hamburg. Các kết quả tính toán của phần mềm FlutterBK02(a) phù hợp với các kết quả thực nghiệm.
ĐIỀU KHIỂN THỤ ĐỘNG DAO ĐỘNG FLUTTER CỦA
DẦM CHỦ CẦU TREO BẰNG PHƢƠNG PHÁP KHÍ
ĐỘNG
Trong chương này trình bày điều khiển thụ động dao động flutter
của dầm chủ cầu treo bằng cách sử dụng 2 cánh vẫy.
5.1 Thiết lập phƣơng trình chuyển động
5
Hình 5.1 Mô hình tính toán của hệ dầm cầu-2 cánh vẫy
Phương trình chuyển động:
m
m1 m2 h m2e2 m1e1 khh chh Lh Lw1 Lw2 (5.15)
m2e2 m1e1 h I m1e12 m2e22 k kw1 w1 kw2 w2 (5.16)
c cw1 w1 cw2 w2 M e1 Lw1 e2 Lw2
I1w1 kw1 w1 cw1 w1 Mw1
I 2w2 kw2 w2 cw2 w2 Mw 2
20
(5.17)
(5.18)
5.2 Phƣơng trình lực khí động trong trƣờng hợp dầm cầu và các
cánh vẫy xem nhƣ tấm phẳng
Giả thiết rằng luồng gió thổi qua dầm cầu và cánh vẫy phía sau
không bị ảnh hưởng bởi luồng gió rối phát sinh bởi các vật thể phía
trước. Như vậy phương trình các lực khí động tác dụng lên dầm cầu
và các cánh vẫy được thiết lập một cách độc lập [103, 179].
5.3 Sử dụng phƣơng pháp bƣớc lặp giải hệ phƣơng trình vi phân
chuyển động
Bước 1: Giả thiết chuyển vị xoắn có dạng
(5.35)
0e FF t sin F t
Bước 2: Thay , , vào ba phương trình còn lại, tìm được 6
đại lượng h0 / 0 , w10 / 0 , w20 / 0 , h , , theo hai ẩn số
w1
w2
F , F . Với h0 , w10 , w20 là các biên độ dao động, h , , là
độ lệch pha của các dao động h, w1 , w2 so với dao động xoắn.
Bước 3: Viết lại phương trình dao động xoắn dưới dạng chuẩn
(5.84)
2 F F F2 0
Ta tìm được
w1
w2
B3
h
B2
B2
F m2e2 m1e1 0 F F2 1 sin h 2 F cos h
F A1* e1 w1 F H11* e2 w2 F H12*
2
2
2
0
B3 2 *
h0
Bw21 2 *
Bw2 2 2 * h0
F H 42
sin h c cw1 cw 2
F sin h cos h F A4 e1 F H 41 e2
0
2
2
2
0F
B2
B2
B3
B3
B4
F A2* e12 w1 F H11* e22 w2 F H12* kw1 e1 w1 F2 H 31* w10 sin w1 cw1 e1 w1 F H 21*
2
2
2
2
2
0 F
w10
B3
B3
F sin w1 cos w1 kw2 e2 w2 F2 H 32* w20 sin w 2 cw2 e2 w 2 F H 22*
0
2
2
0 F
w20
F sin w2 cos w2 / 2F I m1e12 m2e22
0
(5.85)
21
B3
h
B2
B2
F2 m2e2 m1e1 0 F2 1 F2 cos h F sin h
F A1* e1 w1 F H11* e2 w2 F H12*
2
2
2
0
B3 2 *
h
h0
B2
B2
F sin h 1 F2
F A4 e1 w1 F2 H 41* e2 w2 F2 H 42* 0 cos h sin h F k kw1
0
2
2
2
0
kw2
B3
B 4 2 * 2 Bw21 2 * 2 Bw2 2 2 *
F A3 e1
F H 41 e2
F H 42 kw1 e1 w1 F2 H 31* w10 cos w1 sin w1 F
2
2
2
2
0
Bw31
B3
F H 21* w10 F sin w1 1 F2 kw2 e2 w2 F2 H 32* w20 cos w 2 sin w 2 F
cw1 e1
2
2
0
0
3
Bw2
F H 22* w20 F sin w 2 1 F2 / I m1e12 m2e22
cw2 e2
2
0
(5.86)
Từ hai phương trình (5.85), (5.86) ta có hệ hai phương trình phi
tuyến với F , F .
5.4 Thí dụ áp dụng
Xét mô hình dầm cầu treo Great Belt với các tham số như trong
mục 3.4.2.
Khi chưa lắp cánh vẫy: U F 40,14(m/s)
Lắp các cánh vẫy với các thông số:
Bw1 Bw2 0,1B, e1 e2 0,5B, cw1 cw2 0 , các cánh vẫy xem
như tấm mỏng hình chữ nhật với khối lượng riêng w 7850kg/m3 ,
có bề dày là 0,02m .
Hình 5.3 Vận tốc gió flutter tới hạn thay đổi theo kw1 , kw2
22
Khi lắp cánh vẫy, vận tốc gió flutter tới hạn lớn nhất theo tính
toán lý thuyết:
U F opt 58(m/s)
Hiệu suất lớn nhất về mặt lý thuyết
58 40,14
*100 44, 49%
40,14
5.5 Kết luận chƣơng 5
Chương 5 trình bầy việc nâng cao vận tốc gió tới hạn bằng cách
lắp hai cánh vẫy vào dầm cầu. Khi lắp hai cánh vẫy vào mô hình mặt
cắt của dầm cầu, ta có hệ cơ học 4 bậc tự do. Trong chương này áp
dụng phương trình Lagrange loại 2 thiết lập phương trình dao động
cho hệ này. Sau đó, phát triển phương pháp bước lặp của M.
Matsumoto và đồng nghiệp cho hệ 2 bậc tự do [117], xây dựng thuật
toán tìm vận tốc gió tới hạn cho hệ 4 bậc tự do. Cuối chương, tính
toán mô phỏng số cho việc lắp hai cánh vẫy vào mô hình mặt cắt của
cầu Great Belt (Đan Mạch). Các kết quả tính toán cho thấy bằng cách
lắp thêm hai cánh vẫy có thể nâng vận tốc flutter tới hạn lên khoảng
45%. Các tài liệu nghiên cứu tính toán lý thuyết loại lắp cánh vẫy bị
động còn ít được nghiên cứu. Tuy nhiên, kết quả tính toán của luận
án khi lò xo đàn hồi có hệ số cứng tăng lên vô hạn trùng với kết quả
đã biết trong tài liệu [35].
KẾT LUẬN VÀ KIẾN NGHỊ
Các kết quả chính của luận án
Các nghiên cứu về dao động của cầu dưới tác dụng của gió được
tiến hành theo hai hướng chính:
- Nghiên cứu thực nghiệm trên mô hình trong phòng thí nghiệm
hầm gió. Sau đó, dùng lý thuyết dao động giải thích các kết quả thu
được.
- Xây dựng mô hình dao động của cầu dưới tác dụng của gió. Áp
dụng lý thuyết dao động tính toán mô hình dao động của cầu dưới tác
dụng của gió. Các nghiên cứu mô hình trong phòng thí nghiệm hầm
gió nhằm xác định một số tham số mô hình và kiểm chứng các kết
quả tính toán lý thuyết.
Công trình nghiên cứu này đi theo hướng thứ hai. Các kết quả
chính của luận án bao gồm các điểm sau đây:
23
1. Dựa trên phương pháp bước lặp của M. Matsumoto và sử dụng
phần mềm MATLAB, đã xây dựng thuật toán và chương trình tính
Flutter-BK01 tính toán vận tốc gió flutter tới hạn. Các kết quả tính
theo chương trình Flutter-BK01 phù hợp với kết quả thực nghiệm ở
trường Đại học Kỹ thuật Hamburg và các kết quả tính một số mô
hình cầu ở Mỹ, Đan Mạch, Trung Quốc đã công bố.
2. Phát triển phương pháp bước lặp của M. Matsumoto từ hệ 2
bậc tự do [117] sang hệ 4 bậc tự do của mô hình mặt cắt dầm chủ của
cầu có gắn các bộ giảm chấn khối lượng-cản (TMD) cơ học. Xây
dựng thuật toán và chương trình tính Flutter-BK02(a), dựa trên phần
mềm MATLAB.
3. Tiến hành nghiên cứu thực nghiệm lắp đặt bộ tắt chấn động lực
vào mô hình cầu của Trường Đại học Kỹ thuật Hamburg. Các kết
quả tính toán vận tốc flutter tới hạn và dao động uốn-xoắn bằng
chương trình Flutter-BK02(a) phù hợp với kết quả thực nghiệm.
4. Áp dụng phần mềm Flutter-BK02(a) tính toán vận tốc tới hạn
flutter mô hình cầu Great Belt của Đan Mạch. Kết quả lắp đặt bộ
giảm chấn khối lượng-cản có thể nâng vận tốc gió tới hạn lên khoảng
80%.
5. Phát triển phương pháp bước lặp của M. Matsumoto từ hệ 2
bậc tự do [117] sang hệ 4 bậc tự do của mô hình mặt cắt dầm cầu có
gắn bộ giảm chấn khí động học (hai cánh vẫy). Xây dựng thuật toán
và chương trình tính Flutter-BK02(b), dựa trên phần mềm
MATLAB. Các kết quả tính toán lý thuyết cho thấy khả năng nâng
cao vận tốc gió tới hạn của cầu.
Các vấn đề cần nghiên cứu tiếp
1. Cần nghiên cứu xây dựng mô hình toàn phần cầu treo dây
văng, dây võng dưới tác dụng của gió có lắp các bộ giảm chấn khối
lượng-cản (TMD) và các bộ giảm chấn khí động (cánh vẫy).
2. Việc nghiên cứu lắp đặt các bộ giảm chấn khối lượng-cản
(TMD) và bộ giảm chấn khí động (cánh vẫy) lên cầu một cách tối ưu
là bài toán khó và cần được nghiên cứu tiếp.
3. Việc nghiên cứu điều khiển chủ động dao động flutter của cầu.
24