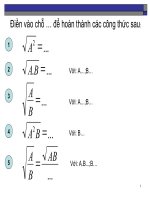Tiết 35 Đại số NC

Tiết 35 Bài 4 Hệ Phương trình bậc nhất nhiều ẩn
1.Hệ phương trình bậc nhất hai ẩn





+=+
+=+
0)
2
b'
2
(a'
'
cy
'
bx
'
a
0)
2
b
2
(acbyax
(I)
* Mỗi cặp số (x0;y0) đồng thời là nghiệm của cả hai phư
ơng trình trong hệ được gọi là một nghiệm của hệ.
* Giải hệ phương trình là tìm tất cả các nghiệm của nó.
* Các khái niệm hệ phương trình tương đương ,hệ phư

ơng trình hệ quả cũng tương tự đối với phương trình.
H1
Giải các hệ phương trình sau:



=+
=
53
152
)
yx
yx
a



=
=+
23
262
)
yx
yx
b

=
=
3
1
3
1
13
)
yx
yx
c
a) Hệ phương trình có một nghiệm duy nhất (x;y)=(2;1)
b) Hệ phương trình vô nghiệm
c) Hệ phương trình có vô số nghiệm

Gi¶ sö (d) lµ ®­êng th¼ng ax+by=c vµ (d’) lµ ®­êng th¼ng a’x+b’y=c’
HÖ (I) cã nghiÖm duy nhÊt
⇔ (d) vµ (d’) c¾t nhau
HÖ (I) v« nghiÖm
⇔ (d) vµ (d’) song song víi nhau
HÖ (I) v« sè nghiÖm
⇔ (d) vµ (d’) trïng nhau

2.Giải và biện luận hệ phương trình bậc nhất hai ẩn
a)Xây dựng công thức

+=+
+=+
0)
2
b'
2
(a'
'
cy
'
bx
'
a
0)
2
b
2
(acbyax
(I)
D=ab-ab, Dx=cb-cb và Dy=ac-ac
1) D0:Hệ có một nghiệm duy nhất (x;y), trong đó
D
y
D
y;
D
x
D
x ==
2) D=0:

Dx 0 hoặc Dy0:Hệ vô nghiệm.

Dx=Dy=0:Hệ có vô số nghiệm ,tập nghiệm của hệ là
tập nghiệm của phương trình ax+by+c=0.

b)Thực hành giải và biện luận
a
a
x
x
+
+
b
b
y
y
=
=
c
c
Biểu thức pq-pq ,với p, q, p, q là những số , được gọi
là một định thức cấp hai và kí hiệu là
q'p'
qp
D=
= ab-ab
a
a
x

x
+
+
b
b
y
y
=
=
c
c
Dx=
= cb-cb
a
a
x
x
+
+
b
b
y
y
=
=
c
c
Dy=
= ac-ac
H3: Trong định thức D, cột

thứ nhất gồm các hệ số của
., cột thứ hai gồm các hệ
số của .
Phát biểu tương tự đối với Dx
và Dy.
b
b
a
a
c
c
b
b
a
a
c
c

5x - 2y = -9
4x + 3y = 2
VÝ dô 1.Gi¶i hÖ ph­¬ng tr×nh :
Gi¶i. Ta cã:
5
4
-2
3
D = = 5.3- 4.(-2)=23 ≠ 0;
-9
2
-2

3
Dx = = -9.3-2.(-2)=-23 ;
5
4
-9
2
Dx = = 5.2- 4.(-9)=46;
1;
D
x
D
x ra suy −==
2;
D
y
D
y ra suy ==
VËy HPT cã mét nghiÖm duy nhÊt (x;y)=(-1;2).