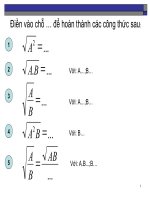Tiết 53 Đại số 9 Công thức nghiệm PT bậc 2

GI¸O ¸N §IÖN Tö
Môn: Đại Số 9
NGƯỜI THỰC HIỆN
Gi¸o viªn: §oµn Quèc ViÖt
Tr­êng THCS Nh©n Hoµ
PHÒNG GIÁO DỤC HUYỆN VĨNH BẢO – HẢI PHÒNG
TRƯỜNG THCS NHÂN HOÀ
Tiết 53
Tiết 53
:
:
Công thức nghiệm
Công thức nghiệm
của phương trình bậc hai
của phương trình bậc hai
KIỂM TRA BÀI CŨ
Thứ 4 ngày 8 tháng 3 năm 2008
Bài 14 SGK trang 43:
Giải:
(1)
2x
2
+ 5x + 2 = 0 (1)
2x
2
+ 5x = -2
⇒
Giải phương trình sau:
x
2
+ x =

5
2
⇒
-1
2
x
2
+ 2.x. + = +
5
4
5
4
( )
2
5
4
( )
2
⇒
-1
2
(x + )
2
= =
5
4
17
16
⇒
( )

2
17
4
x + = ±
5
4
⇒
17
4
⇒
x =
-5 + 17
4
-5 - 17
4
hoặc x =
Tiết 53: CÔNG THỨC NGHIỆM CỦA PHƯƠNG TRÌNH BẬC HAI
Thứ 4 ngày 8 tháng 3 năm 2008
1. Công thức nghiệm
Biến đổi phương trình ax
2
+bx+c=0 (a ≠0)
bằng cách điền vào chỗ trống (.......). (các
bước như bài kiểm tra bài cũ)
2x
2
+ 5x + 2 = 0 (1)
2x
2
+ 5x = -2

x
2
+ x =
5
2
x
2
+ 2.x. + = +
5
4
5
4
( )
2
5
4
( )
2
⇒
⇒
(x + )
2
= =
5
4
17
16
⇒
x + = ±
5

4
⇒
⇒
⇒
Giải phương trình sau:
b
a
-c
a
( )
2
b
2a
b
2
- 4ac
4a
2
ax
2
+bx+c = 0
⇒
⇒
⇒
⇒
x
2
+...x = ....
ax
2

+ bx = ...
x
2
+ 2.x. + = + ......
( )
2
b
2a
b
2a
-c
a
(x + )
2
= ............
b
2a
-1
2
-1
2
( )
2
17
4
17
4
Kí hiệu
∆
= b

2
– 4ac
∆
4a
2
⇒
(x + )
2
= ......
b
2a
x =
-5 + 17
4
-5 - 17
4
hoặc x =
-c
Tiết 53: CÔNG THỨC NGHIỆM CỦA PHƯƠNG TRÌNH BẬC HAI
Thứ 4 ngày 8 tháng 3 năm 2008
1. Công thức nghiệm
ax
2
+bx+c = 0 (a≠0) (1)
Với ∆ = b
2
– 4ac
(x + )
2
=

∆
4a
2
b
2a
⇒
(2)
?1 Hãy điền những biểu thức thích hợp vào chỗ trống (......) dưới đây:
a, Nếu ∆ > 0 thì từ phương trình (2) suy ra x + = ± .......
b
2a
do đó, phương trình (1) có hai nghiệm x
1
= ............ , x
2
= ............
b, Nếu ∆ = 0 thì từ phương trình (2) suy ra x + = ....
do đó, phương trình (1) có nghiệm kép x = .......
b
2a
-b + ∆
2a
-b - ∆
2a
∆
2a
0
-b
2a
?2 Hãy giải thích vì sao khi ∆ < 0 thì phương trình (2) vô nghiệm.

Tiết 53: CÔNG THỨC NGHIỆM CỦA PHƯƠNG TRÌNH BẬC HAI
Thứ 4 ngày 8 tháng 3 năm 2008
1. Công thức nghiệm
Đối với phương trình ax
2
+bx+c = 0 (a≠0) và biệt thức ∆ = b
2
-4ac
•
Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt:
-b + ∆
2a
x
1
=
-b - ∆
2a
x
2
=
•
Nếu ∆ = 0 thì phương trình có nghiệm kép x
1
= x
2
=
-b
2a
•
Nếu ∆ < 0 thì phương trình vô nghiệm.