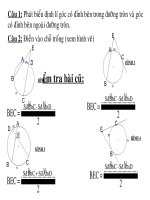
Goc co dinh o trong hay ngoai d­uong tron

1, Cho đường tròn (O) , A, B,
C thuộc đường tròn , Ax là
tiếp tuyến của đường tròn
(Như hình vẽ ) :
Xác định góc ở tâm , góc nội
tiếp , góc tạo bởi tia tiếp
tuyến và dây cung .
Viết biểu thức tính số đo các
góc đó theo cung bị chắn . So
sánh các góc đó
2, Phát biểu định lý , hệ quả về góc
tạo bởi tia tiếp tuyến và dây cung
1, Trên hình có :
- Góc AOB là góc ở tâm
_ góc ACB là góc nội tiếp
- Góc BAx là góc giữa một tia tiếp
tuyến và dây cung
AOB = sđ AB (cung AB nhỏ )
ACB = sđ AB (cung AB nhỏ )
BAx = sđ AB
=> AOB = 2 ACB = 2 BAx
ACB = BAx
2
1
2
1
2, Số đo của góc tạo bởi một tia tiếp tuyến
và dây cung bằng nửa số đo của cung bị
chắn

Trong một đường tròn , góc tạo bởi tia tiếp
tuyến và dây cung và góc nội tiếp cùng
chắn một cung thì bằng nhau
X
B
C
O
A

Gãc cã ®Ønh ë bªn trong ®­êng trßn
Gãc cã ®Ønh ë bªn ngoµi ®­êng trßn
1, Gãc cã ®Ønh ë bªn trong ®­êng trßn
Gãc BEC cã ®Ønh E n»m bªn trong ®­êng trßn ( O)
®­îc gäi lµ gãc cã ®Ønh n»m trong ®­êng trßn
Gãc BEC ch¾n cung BnC vµ cung DmA
Gãc ë t©m lµ gãc cã ®Ønh n»m trong ®­êng
trßn nã ch¾n hai cung b»ng nhau
AOB ch¾n hai cung AB vµ CD
j
n
m
O
E
D
C
B
A
O
C
D

B
A

Góc có đỉnh ở bên trong đường tròn
Góc có đỉnh ở bên ngoài đường tròn
Định lí : Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo
hai cung bị chắn
Chứng minh
Nối BD . Theo định lí góc nội tiếp
BDE = Sđ BnC ; DBE = Sđ AmD
Mà BDE + DBE = BEC ( góc ngoài của tam giác )
=> BEC =
2
1
2
1
2
SdDmASdBnC+
j
n
m
O
E
D
C
B
A
1, Góc có đỉnh ở bên trong đường tròn
GT
KL

Cho đường tròn (O)
Góc BEClà góc có đỉnh ở
trong đường tròn
BEC =
2
sdDmAsdBnC +

Góc có đỉnh ở bên trong đường tròn
Góc có đỉnh ở bên ngoài đường tròn
1, Góc có đỉnh ở bên trong đường tròn
2, Góc có đỉnh ở bên ngoài đường tròn
Đặc điểm của góc :
- Đỉnh nằm ngoài đường tròn
- Các cạnh đều có điểm chung với đường tròn (có 1 điểm chung hoặc hai điểm
chung )
k
n
A
E
C
O
Góc BEC có hai cạnh cắt đư
ờng tròn , hai cung bị chắn là
hai cung nhỏ AD và BC
Góc BEC có một cạnh là
tiếp tuyến và cạnh kia là cát
tuyến , hai cung bị chắn là
hai cung nhỏ AC và CB
Góc BEC có hai cạnh là
hai tiếp tuyến tại Avà C

hai cung bị chắn là cung
nhỏAC và cung lớn AC
m
O
D
C
E
A
B
E
O
C
A
B