Tiết 48: Tứ giác nội tiếp

1) Vẽ một đường tròn tâm O rồi vẽ một tứ giác có tất
cả các đỉnh nằm trên đường tròn đó.
2) Vẽ một đường tròn tâm I rồi vẽ một tứ giác có ba
đỉnh nằm trên đường tròn đó còn đỉnh thứ tư thi
không.
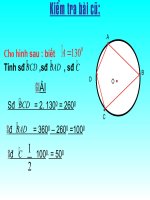
Kiểm tra bài cũ:
3) Phát biểu kết luận quỹ tích Cung chứa góc
dựng trên đoạn thẳng AB.
Khi = 90
0
->quỹ tích cung chứa góc 90
0
là gi

TiÕt 48:
TiÕt 48:
Tø gi¸c néi tiÕp
Tø gi¸c néi tiÕp

1/định nghĩa :Một tứ giác có
bốn đỉnh nằm trên một đư
ờng tròn được gọi là tứ giác
nội tiếp đường tròn đó.(Gọi
tắt là tứ giác nội tiếp)
C
A
B

D
O
.
Ví dụ: Tứ giác ABCD
là tứ giác nội tiếp

Tứ giác MNBF,
MNAF, FNBA được
gọi là tứ giác nội tiếp
đường tròn (I).
TứgiácMNE F, MNQF
không là tứ giác nội tiếp đư
ờng tròn (I).
?Trong hnh vẽ sau :Tứ giác nào được gọi là tứ
giác nội tiếp đường tròn?V sao?
N
M
E
B
A
F
I
Q




Bµi to¸n:Cho tø gi¸c ABCD néi
tiÕp ®­êng trßn .Chøng minh :
^

Α
0
0
180
180
C
^
^
B
+
^
D
+
=
=

A
B
C
O
Chøng minh: Cã tứ giac ABCD n i ộ
ti p ng tron t©m O(gt)ế đườ
360
0
.
D
=>
=
Α
^

2
1
s®BCD
(®.lÝgãc néi tiÕp)
=
s®DAB
^
C
2
1
(®.lÝgãc néi tiÕp)
͡
^
^
=
+
A
C
2
1
s®BCD
+
͡
s®DAB
=
2
1
=
180
0

(t/c tø gi¸c)
^
B
A
^
+
+
=
C
^
D
^
+
Do
360
0
B
^
D
^
+
suy ra
=
180
0


2.®ÞnhlÝ:Trong
mét tø gi¸c néi
tiÕp, tæng sè ®o

hai gãc ®èi diÖn
b»ng
0
180

M
N
P
Q
O
0
100
0
70
Tø gi¸c MNPQ néi tiÕp
®­êng trßn t©m O.
a.Sè ®o c¸c gãc trªn hnh vÏ
®óng hay sai?
®¸p ¸n: a.Sai

Cñng cè
Bµi1
b.
=
100
0
^
M
P = ?
^

⇒
b.
^
=
80
0
P

Góc A
Góc B
Góc C
Góc D
0
120

0
115
0
105
0
110
0
130


0
180
Bài 2 : Biết ABCD là tứ giác nội tiếp đường
tròn.Hãy điền vào ô trống trong bảng sau:
Trường hợp

Góc
2)
3)
0
50
0
60
0
75
0
70
1)

< <
0 0
(0 180 )
0
65

NÕu mét tø gi¸c cã tæng
sè ®o hai gãc ®èi nhau
b»ng th tø gi¸c ®ã
néi tiÕp ®­îc ®­êng trßn.
3.®Þnh lÝ ®¶o:
0
180

C¸c b­íc chøng minh:
O
D

C
B
A
-VÏ ®­êng trßn
t©m O ®i qua ba
®iÓm A,B,C
Tø gi¸c ABCD cã:
-C/m ®iÓm D
còng thuéc (O)
180
0
+
B
^
D
^
=