Ôn tập THPT 2019 hình học 12 bài 2

Câu 1: [2H1-2-4] (Lớp Toán - Đoàn Trí Dũng -2017 - 2018) Cho tứ diện ABCD có độ dài
cạnh AB  x và tất cả các cạnh còn lại đều có độ dài bằng 1. Tìm giá trị của x biết
1
rằng thể tích của tứ diện ABCD bằng ?
8
A

x

D

B

C

B. x 

A. x  1 .

1
.
2

C. x 

6
.
3

D. x 

6
2

Lời giải
Chọn D

abc
1  cos 2   cos 2   cos 2   2cos  cos  cos  và
6
ứng dụng với độ dài các cạnh CA  a  1, CB  b  1, CD  c  1 , các giá trị
Ta xét công thức: V 

cos ACB 

2  x2
1
;cos ACD  cos DCB  .
2
2
2

Khi đó: VABCD

1
1 1  2  x2 
1 1  2  x2  1
6
.

1   


2


  x
6
4 4  2 
2 2 2  8
2

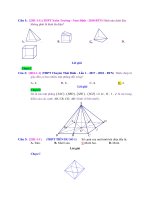
Câu 2: [2H1-2-4] (Lớp Toán - Đoàn Trí Dũng -2017 - 2018) Một nhà toán học muốn điêu
khắc một bức tượng đặc biệt có dạng “xoắn” được cắt gọt từ một khối đá hình lăng
trụ tam giác đều ABC.A ' B ' C ' có tất cả các cạnh đều bằng 1. Biết rằng bức tượng
đó có hai đáy là các tam giác ABC và A ' B ' C ' đồng thời thiết diện của bức tượng
khi cắt bởi một mặt phẳng bất kỳ song song và nằm giữa hai đáy là một tam giác
có ba đỉnh lần lượt nằm trên các đường chéo AC ', CB ' và BA ' . Xác định thể tích
V của bức tượng đá mà nhà toán học dự định điêu khắc.


C'

A'

B'
M
N
C

A
P

B
A. V 

3
.
8

B. V 

3
.
12

C. V 

3 3
.
32

D. V 

3
6

Lời giải

Chọn A
Chọn trục tọa độ Ax trùng với tia AA ' với gốc tọa độ A và xét thiết diện ở vị trí
độ cao cách mặt đáy một khoảng x .

Chiếu MNP xuống mặt phẳng  ABC  ta được IEH như hình vẽ.
Khi đó theo định lý Thales:

HB PH x

  HB  x .
AB AA 1

 EC  x
Tương tự  
.
 BE  1  x
Hàm dụng định lí cosin cho BHE ta được:


HE  x 2  1  x   2 x. 1  x  .cos 60  3 x 2  3 x  1 .
2

 SMNP  SIEH  HE 2 .

3
3

3x 2  3x  1 .

4
4
1

3

3
3x 2  3x  1 dx 
.

4
8

Vậy thể tích vật thể cần tính là: V  
0

Hình ảnh bên phải là hình ảnh chính xác của vật thể mà bài toán đang đề cập tới.

(Bài toán của tác giả Đoàn Trí Dũng)
Câu 3: [2H1-2-4] (Đề thi lần 6- Đoàn Trí Dũng - 2017 - 2018)Một nhà toán học muốn điêu
khắc một bức tượng đặc biệt có dạng “xoắn” được cắt gọt từ một khối đá hình lăng
trụ tam giác đều ABC.ABC có tất cả các cạnh đều bằng 1 . Biết rằng bức tượng
đó có hai đáy là các tam giác ABC và ABC đồng thời thiết diện của bức tượng
khi cắt bởi một mặt phẳng bất kỳ song song và nằm giữa hai đáy là một tam giác
có ba đỉnh lần lượt nằm trên các đường chéo AC , CB và BA . Xác định thể tích
V của bức tượng đá mà nhà toán học dự định điêu khắc.
A'

C'

B'
M
N
A

C

P

B

A. V 

V

3
.
8

B. V 

3
.
12

C. V 

3
.
6
Lời giải

Chọn A

3 3
.
32

D.


C'
A'

B'
M

A

I

N
C
E

P
H
B

Chọn trục tọa độ Ax trùng với tia AA với gốc tọa độ A và xét thiết diện ở vị trí độ
cao cách mặt đáy một khoảng x .
Chiếu MNP xuống mặt phẳng  ABC  ta được IEH như hình vẽ.
Khi đó theo định lý Thales ta có

HB PH x

  HB  x .

AB AA 1

 EC  x
Tương tự ta có 
.
 BE  1  x
Áp dụng định lí Cô-sin cho BHE ta có HE  x 2  1  x   2 x. 1  x  .cos 60o
2

 3x 2  3x  1 .
SMNP  SIEH  HE 2 .

3
3

3x 2  3x  1 .

4
4
1

Vậy thể tích vật thể cần tính là: V  
0

3
3
3x 2  3x  1 dx 
.

4

8

Hình ảnh bên dưới là hình ảnh chính xác của vật thể mà bài toán đang đề cập tới.

BẢNG ĐÁP ÁN
1.A
11.B
21.A
31.C
40.A

2.
12.
22.A
32.C
41.

3.
13.A
23.A
33.A
43.

4.C
14.C
24.A
34.
44.

5.C

15.A
25.B
35.A
45.B

6.B
16.
26.A
36.
46.

7.B
17.B
27.B
37.C
47.B

8.A
18.B
28.B
38.
48.A

9.B
19.C
29.C
39.B
49.

10.B

20.
30.B
40.B
50.A


Câu 4: [2H1-2-4] [LẠNG GIANG SỐ 1-2017] Cho khối tứ diện đều ABCD cạnh bằng
2cm. Gọi M , N , P lần lượt là trọng tâm của ba tam giác ABC , ABD, ACD. Tính
thể tích V của khối chóp AMNP.

2 3
cm .
162
2 3
V
cm .
144

A. V 

B. V 

2 2 3
cm .
81

C. V 

4 2 3
cm .

81

Lời giải

Chọn C

A

N
M
B

P

K

D
H

E

F
C

Tam giác BCD đều  DE  3  DH 

AH  AD2  DH 2 

2 3
3

2 6
3

1
1 1
1
3
SEFK  .d E , FK  .FK  . d D,BC . BC 
2
2 2
2
4
 VSKFE 
Mà

1
1 2 6 3
2
.
AH .SEFK  .
.

3
3 3 4
6

AM AN AP 2




AE AK AF 3

D.


Lại có:

VAMNP AM AN AP 8
8
4 2
.

.
.

 VAMNP  VAEKF 
VAEKF
AE AK AF 27
27
81

Câu 5: [2H1-2-4][CHUYÊN BIÊN HÒA-2017] Cho hình chóp tứ giác đều S.ABCD có
cạnh đáy bằng a , cạnh bên hợp với đáy một góc 60 . Gọi M là điểm đối xứng

của C qua D , N là trung điểm SC. Mặt phẳng  BMN  chia khối chóp S.ABCD
thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng:
A.

7

.
5

1
.
7

B.

C.

7
.
3

D.

6
.
5

Lời giải
Chọn A
S

N
E
H

D

C
O

B

M

F

A

Giả sử các điểm như hình vẽ.

E  SD  MN  E là trọng tâm tam giác SCM , DF // BC  F là trung điểm
BM .





Ta có: SD,  ABCD   SDO  60  SO 

 d  O,  SAD    OH  h 

a 6
a 7
, SF  SO 2  OF 2 
2
2

a 6
1
a2 7
; SSAD  SF .AD 
2
4
2 7

VMEFD ME MF MD 1




VMNBC MN MB MC 6
 VBFDCNE

5
5 1
1
5
1
5a3 6
 VMNBC    d  M ,  SAD    SSBC   4h  SSAD 
6
6 3
2
18
2
72

1
a3 6
7a3 6
VS . ABCD  SO.S ABCD 
 VSABFEN  VS . ABCD  VBFDCNE 

3
6
36


Suy ra:

VSABFEN 7
 
VBFDCNE 5

Câu 6: [2H1-2-4][CHUYÊN PHAN BỘI CHÂU-2017] Khối chóp S.ABCD có đáy
ABCD là hình thoi cạnh a . SA  SB  SC  a , Cạnh SD thay đổi. Thể tích lớn
nhất của khối chóp S.ABCD là:
A.

a3
.
8

B.

a3

.
4

C.

3a 3
.
8

D.

a3
.
2

Lời giải

Chọn D
S

A

B

x

O

a

H

C

D

Khi SD thay đổi thi AC thay đổi. Đặt AC  x . Gọi O  AC  BD .
Vì SA  SB  SC nên chân đường cao SH trùng với tâm đường tròn ngoại tiếp
tam giác ABC  H  BO .
2

x
Ta có OB  a    
2
2

4a 2  x 2

4

4a 2  x 2
2

1
1
4a 2  x 2 x 4a 2  x 2
S ABC  OB. AC  x.

2
2

2
4
HB  R 

a.a.x

4S ABC

a2 x
x 4a 2  x 2
4.
4



a2
4a 2  x 2

.

a4
a 3a 2  x 2
SH  SB  BH  a  2 2 
4a  x
4a 2  x 2
2

2

2

1
2 a 3a 2  x 2 x 4a 2  x 2
VS . ABCD  2VS . ABC  2. SH .S ABC  .
.
3
3 4a 2  x 2
4





1
1  x 2  3a 2  x 2  a 3
 a x. 3a 2  x 2  a 

3
3 
2
 2
Câu 7: [2H1-2-4] Cho hình chóp tứ giác đều S .ABCD có cạnh đáy bằng a , cạnh bên hợp
với đáy một góc 60 . Gọi M là điểm đối xứng với C qua D ; N là trung điểm
của SC , mặt phẳng ( BMN ) chia khối chóp S .ABCD thành hai phần. Tính tỉ số
thể tích giữa hai phần đó.
A.

1
.

5

B.

7
.
3

C.

1
.
7

D.

Lời giải

Chọn D
S

N

60°

A

B

K

I

a

O
H

M

Đặt

V1
V2

VSABIKN
VNBCDIK

D

V1

1 a 6 2
.
a
3 2

* VN .BMC

1
.NH .S

3

6 3
a .
6

BMC

1 SO
.
.S
3 2

1a 6 1
. .a.2a
3 4 2

BMC

* Nhận thấy K là trọng tâm của tam giác SMC

*

VM .DIK
VM .CBN

C

?.

V2

* VS .ABCD

a

MD MI MK
.
.
MC MB MN

1 1 2
. .
2 2 3

1
.
6

MK
MN

2
.
3

6 3
a .
12

7
.
5


V2

VM .CBN

V1

VS .ABCD

5
V
6 M .CBN

VM .DIK

6 3
a
6

V2

5 6 3
.
a
6 12

5 6 3
a
72

5 6 3
a .
72

7 6 3
a
72

7 6 3
a
72
5 6 3
a
72

V1
V2

7
.
5

Câu 8: [2H1-2-4] Cho hình chóp tứ giác S.ABCD có SA   ABCD  , ABCD là hình thang
vuông tại A và B biết AB  2a , AD  3BC  3a . Tính thể tích khối chóp
S.ABCD theo a , biết khoảng cách từ A đến mặt phẳng ( SCD ) bằng

A. 6 6a 3 .

C. 2 3a 3 .

B. 2 6a 3 .
Lời giải

Chọn B
S

K

D

A
M
B

Dựng AM  CD tại M .
Dựng AH  SM tại H .

3 6
a.
4
AD  BC

. AB  4a 2
2

Ta có: AH 

S ABCD

CD 

 AD  BC 

S ABC 

1
AB.BC  a 2
2

2

 AB 2  2a 2

S ACD  S ABCD  S ABC  3a2

C

3 6
a.
4
D. 6 3a 3 .


2S
1
3 2
AM .CD  AM  ACD 

a
2
CD
2
1
1
1
AH . AM
3 6
Ta có:


 AS 

a
2
2
2
2
2
AH
AM
AS
2
AM  AH
1
VS . ABCD  SA.S ABCD  2 6a 3
3
S ACD 

Câu 9: [2H1-2-4] Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi A là

SA 3
 . Mặt phẳng  P  đi qua A và song song với
SA 4
 ABCD  cắt SB , SC , SD lần lượt tại B , C , D . Mặt phẳng  P  chia khối

điểm trên cạnh SA sao cho

chóp thành hai phần. Tỉ số thể tích của hai phần đó là:
A.

37
.
98

B.

27
.
37

C.

4
.
19

D.

27
.
87

Lời giải
Chọn B

2

V
SA ' SB ' SC '  3 
27
.
.
  
Ta có: S . A ' B ' C ' 
VS . ABC
SA SB SC  4 
64
Do đó

VS . A ' B ' C '
V
27
27
; tương tự S . D ' B ' C ' 

VDBC .D ' B ' C ' 37
VABC . A ' B ' C ' 37

Theo tính chất dãy tỉ số bằng nhau suy ra:

VS . A ' B ' C '
V
VS . A ' B ' C '  VS .D ' B ' C '
27
.
 S .D ' B ' C ' 

VABC . A ' B ' C ' VDBC .D ' B ' C ' VABC . A ' B ' C '  VDBC .D ' B ' C ' 37
Câu 10: [2H1-2-4] Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a 3 . Gọi M , N
lần lượt là trung điểm của SB, BC Tính thể tích khối chóp A.BCNM . Biết mặt
phẳng  AMN  vuông góc với mặt phẳng  SBC  .


A.

a 3 15
.
32

B.

3a3 15
.
32

C.

3a3 15

.
16

D.

3a3 15
.
48
Lời giải
Chọn B

E là trung điểm BC nên CB  AE , CB  SH


 CB   SAE   CB  SE .
SE vừa là trung tuyến vừa là đường cao nên SBC cân tại S
F là giao điểm của MN với SE 
 SF  MN , SF 

1
SE .
2


 AMN    SBC 
SF  MN


 SF   AMN 
AMN


SBC

MN







Giả thiết 

1
3a
 SE  AF và SF  SE nên SAE cân tại A  AE  AS 
2
2
2
2 3a
a 5
AH  AE  .  a 
 SH  SA2  AH 2 
3
3 2
2
3
2
1
1

3 a 5 a 15
.
VS . ABC  S ABC .SH  . a 3
.

3
3
4 2
8
VS . AMN SM SN 1
a3 15
.

.
 
VS . AMN 
VS . ABC
SB SC 4
32



Vậy V  VS . ABC  VS . AMN



3a3 15
.

32

Câu 11: [2H1-2-4] Cho hình chóp tứ giác đều S.ABCD Mặt phẳng  P  qua A và vuông
góc SC cắt SC , SB, SD lần lượt tại B, C, D . Biết rằng 3SB  2SB . Gọi V1 ,V2
lần lượt là thể tích hai khối chóp S . ABCD và S.ABCD . Tỉ số

V1
là
V2


A.

V1 2
 .
V2 3

B.

V1 2
 .
V2 9

C.

V1 4
 .
V2 9

D.

V1 1

V2 3

.
Lời giải
Chọn D

SB ' 2
SD ' 2
SC '
 
 , bây giờ cần tìm
SB 3
SD 3
SC
Tọa độ hóa với Ox  OC, Oy  OB, OS Oz và đặc biệt hóa cho OA  1
Ta có


 A  1;0;0 


C 1;0;0  , S  0;0; a   SC  1;0; a 
  P  :  x  1  az  0  x  az  1  0 .
x  0

Ta có B  0;1;0   SB   0;1; a   SB :  y  1  t
 z  at





Cho giao với  P   a 2t  1  0  B '  0;1 

t   .

1 1
; .
a2 a 

Ta có

3

3


 a 2  2
1 1
 S 0;0; 3


3  0;1  2 ;  a   2  0;1;  a   
a 3
a a


 3  3a  2a
 P  : x  z 3  1  0

 a





Cho SC giao với

VS . AB ' C ' 2 1 1
 . 
V
1
3 2 3
3
SC ' 1
1
 S . ABC
 
 VS . AB ' C ' D '  VS . ABCD
 P   C '  ;0;  
2 
SC 2 VS . AC ' D ' 1 2 1
3
2
 . 
 VS . ACD
2 3 3
.

Câu 12: [2H1-2-4] (SGD Bắc Ninh - Lần 1 - 2017 - 2018 - BTN) Cho hình chóp S.ABCD
có đáy ABCD là hình vuông cạnh 2a . Tam giác SAB vuông tại S và nằm trong
mặt phẳng vuông góc với đáy. Gọi  là góc tạo bởi đường thẳng SD và mặt
phẳng  SBC  , với   45 . Tìm giá trị lớn nhất của thể tích khối chóp S.ABCD .
A. 4a 3

B.

8a 3
3

C.

4a 3
3

D.

2a 3
3

Lời giải
Chọn C

S

D'

D
A

H
B

C

Gọi D là đỉnh thứ tư của hình bình hành SADD .
Khi đó DD//SA mà SA   SBC  (vì SA  SB , SA  BC ) nên D là hình chiếu
vuông góc của D lên  SBC  .
Góc giữa SD và  SBC  là   DSD  SDA , do đó SA  AD.tan   2a.tan  .
Đặt tan   x , x   0;1 .
Gọi H là hình chiếu của S lên AB , theo đề ta có
1
1
VS . ABC D  .S ABC D .SH  4a 2 .SH .
3
3
Do đó VS . ABCD đạt giá trị lớn nhất khi SH lớn nhất. Vì tam giác SAB vuông tại S
nên SH 

2
2
2ax 4a 2  4a 2 x 2
SA.SB SA. AB  SA


 2ax 1  x 2
AB
2a
AB

x2  1  x2
 2a
a
2

2
.
2
1
4
 .a.4a 2  a 3 .
3
3

Từ đó max SH  a khi tan  
Suy ra max VS . ABCD


Câu 13: [2H1-2-4] Cho tứ diện ABCD , trên các cạnh BC , BD , AC lần lượt lấy các điểm
3
M , N , P sao cho BC  3BM , BD  BN , AC  2 AP . Mặt phẳng  MNP 
2
V
chia khối tứ diện ABCD thành hai phần có thể tích là V1 , V2 . Tính tỉ số 1 .
V2
A.

V1 26
.


V2 13

B.

V1 26
.

V2 19

C.

V1 3
 .
V2 19

D.

V1 15
 .
V2 19
Lời giải
Chọn B
A

Q

P

I
D

N

B
M
C

Gọi VABCD  V , I  MN  CD , Q  IP  AD ta có Q  AD   MNP  .
Thiết diện của tứ diện ABCD được cắt bởi mặt phẳng  MNP  là tứ giác MNQP .
Áp dụng định lí Menelaus trong các tam giác BCD và ACD ta có:
NB ID MC
ID 1
ID PC QA
QA
. .
 và
1 
.
.
 4.
1 
ND IC MB
IC 4
IC PA QD
QD

Áp dụng bài toán tỉ số thể tích của hai khối chóp tam giác, ta có:

VANPQ
VANCD



AP AQ 2
2
1
2
2
  VANPQ  VANCD  V . Suy ra VN . PQDC  V  V
.
AC AD 5
15
3
5
15

1
 V.
5

và

1
2
VCMNP CM CP 1

  VCMNP  VCBNA  V .
.
3
CB CA 3

9
VCBNA

Suy ra V2  VN .PQDC  VCMNP 

19
26
V 26
V . Do đó V1  V  V2  V . Vậy 1 
.
45
45
V2 19


Câu 14: ---------HẾT--------- [2H1-2-4] (SGD - Bắc Ninh - 2017 - 2018 - BTN) Cho tứ
diện đều ABCD có cạnh bằng 1 . Gọi M , N là hai điểm thay đổi lần lượt thuộc
cạnh BC , BD sao cho  AMN  luôn vuông góc với mặt phẳng  BCD  . Gọi V1 ,
V2 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN .

Tính V1  V2 .
A.

17 2
.
216

B.

17 2

.
72

C.

17 2
.
144

D.

2
.
12

Lời giải
Chọn A

Gọi H là tâm tam giác BCD , ta có AH   BCD  , mà

 AMN    BCD 

nên

AH   AMN  hay MN luôn đi qua H .
Ta có BH 

1
6
3

.
 AH  AB2  BH 2  1  
3
3
3

Thể tích khối chóp

ABMN

1
1 6 1
là V  . AH .S BMN  .
. BM .BN .sin 60
3
3 3 2

2
BM .BN .
12
Do MN luôn đi qua H và M chạy trên BC nên BM .BN lớn nhất khi M  C hoặc


N  D khi đó V1 

2
.
24

+ BM .BN nhỏ nhất khi MN //CD khi BM  BN 

Vậy V1  V2 

17 2
.
216

2
2
.
 V2 
3
27


Câu 15: [2H1-2-4] (THPT Yên Lạc - Vĩnh Phúc- Lần 3 - 2017 - 2018 - BTN) Cho hình
chóp S.ABCD có thể tích bằng V , đáy ABCD là hình bình hành. Mặt phẳng  P 
song song với  ABCD  cắt các đoạn SA , SB , SC , SD tương ứng tại M , N , E ,
F

( M , N , E , F khác S và không nằm trên  ABCD  ). Các điểm H , K , P , Q tương
ứng là hình chiếu vuông góc của M , N , E , F lên  ABCD  . Thể tích lớn nhất của
khối đa diện MNEFHKPQ là:
A.

2
V.
3

B.

4
V.
27

C.

4
V.
9

D.

2
V.
9

Lời giải
Chọn C

Đặt k 

SM
SM
. Ta có: MNEF và ABCD đồng dạng với tỉ số k 
SA
SA

 0  k  1 .

Do đó SMNEF  k 2 S ABCD .

Gọi SI là đường cao của S.ABCD . Ta có:

MH MA SA  SM


 1 k .
SI
SA
SA

VMNEFHKPQ  SMNEF .MH  S ABCD .k 2 .(1  k ).SI  3V .k 2 .(1  k )
3V
3V  k  k  2  2k  4

.k .k .(2  2k ) 
.
  V.
2
2 
3
 9
3

Vậy thể tích lớn nhất của khối đa diện MNEFHKPQ là
.

4
2
V khi k  2  2k  k 
9

3


Câu 16: [2H1-2-4] (Chuyên Phan Bội Châu - Nghệ An - Lần 1 - 2017 - 2018 - BTN) Cho
khối tứ diện ABCD có thể tích V . Gọi G1 , G2 , G3 , G4 là trọng tâm của bốn mặt
của tứ diện ABCD . Thể tích khối tứ diện G1G2G3G4 là:
A.

V
.
27

B.

V
.
18

C.

V
.
4

D.

V
.
12

Lời giải
Chọn A
A

G2
G3

G1

I
B

C
G4

J

H1

H2

K

D

Gọi I , J , K lần lượt là trung điểm của BC , BD và DC .
Gọi h là khoảng cách từ A đến  BCD  , h1 là khoảng cách từ G4 đến  G1G2G3  .
Vì  G1G2G3  / /  BCD  nên d  G4 ,  G1G2G3    d  G1 ,  BCD    G1H 2  h , h  AH1
.
h1 KG1 1

h

  h1  .
h
KA 3
3
Gọi S , S  , S1 lần lượt là diện tích các tam giác BCD , IJK và G1G2G3 .


Vì I , J , K lần lượt là trung điểm của BC , BD và DC nên:
1
1 BC 1
JK .d  I , JK   .
. d  D, BC  
2
2 2 2
Tam giác G1G2G3 đồng dạng với tam
S 

1 1
1
. .BC.d  D, BC   S 1 .
4 2
4
giác KIJ với tỉ số đồng dạng là:

G1G2 AG1 2

 .
Ik

Ak
3
2

4
S 2
4
 1      S1  S 
9
S  3  9
dạng).
S
Từ 1 và  2   S1  .
9

 2

(Vì tỉ số diện tích bằng bình phương tỉ số đồng

1
1 S h 1 1
 V
Thể tích khối từ diện G1G2G3G4 là: V1  S1.h1  . .  .  .S .h  
.
3
3 9 3 27  3
 27
Câu 17: [2H1-2-4] (Chuyên Phan Bội Châu - Nghệ An - Lần 1 - 2017 - 2018 - BTN) Cho
tứ diện ABCD có thể tích là V . Điểm M thay đổi trong tam giác BCD . Các

đường thẳng qua M và song song với AB , AC , AD lần lượt cắt các mặt phẳng
 ACD  ,  ABD  ,  ABC  tại N , P , Q . Giá trị lớn nhất của khối MNPQ là:
A.

V
.
27

B.

V
.
16

C.

V
.
8

D.

V
.
54

Lời giải
Chọn A
A

P
Q

B

P
M

Q

N

D

N

C
 Tam giác ABN  có MN // AB 
 Tam giác ACP có MP // AC

MP PM

.
AC PC

 Tam giác ADQ  có QM // AD 
Khi đó:

Mà

MN N M

.
AB
N B

MQ QM

.
AD QD

MN MP MQ N M PM QM





AB AC AD N B PC QD

MN MP MQ
N M PM QM SMCD SMBD SMBC


1






 1 nên
AB AC AD
N B PC QD S BCD S BCD S BCD
3

3
 MN MP MQ   3 MN MP MQ 
Lại có 1  


.
.
 (Cauchy)
  3
AB AC AD 
 AB AC AD  
3

 MN .MP.MQ 

1
MN MP MQ
AB. AC. AD  MN .MP.MQ lớn nhất khi


27
AB AC AD


 M là trọng tâm tam giác BCD 

S NPQ
S N PQ

MN MP MQ 1


   NPQ  //  BCD  ,
AB AC AD 3

2

1
1
2
   , Mà S N PQ  S BCD nên S NPQ  S BCD và
9
4
3

d  M ,  NPQ   

1
d  A,  BCD  
2

1
Vậy giá trị lớn nhất của khối tứ diện MNPQ là VMNPQ  S NPQ .d  M ,  NPQ  
3
1
1 1

1
V
 VMNPQ  . S BCD . d  A,  BCD   
, với VABCD  S BCD .d  A,  BCD    V
3
3 9
3
27

Câu 18: [2H1-2-4] (SGD - Quảng Nam - Lần 1 - 2017 - 2018 - BTN) Cho hình chóp
S.ABCD có đáy ABCD là hình vuông cạnh a , mặt bên SAB là tam giác đều, mặt
bên SCD là tam giác vuông cân tại S . Gọi M là điểm thuộc đường thẳng CD sao
cho BM vuông góc với SA . Tính thể tích V của khối chóp S.BDM .

a3 3
A. V 
.
16

a3 3
B. V 
.
24

a3 3
C. V 
.
32

a3 3

.
V
48
Lời giải
Chọn D

Gọi I , J lần lượt là trung điểm của AB và CD .
Gọi H là hình chiếu của S lên IJ . Ta có SI 

a
a 3
, SJ  , IJ  a .
2
2

Khi đó SI 2  SJ 2  IJ 2 suy ra tam giác SIJ vuông tại S .

D.


Ta

có

AH  SA2  SH 2 

SH 

SI .SJ
SI 2  SJ 2



3
3a
a  HI  SI 2  SH 2 
4
4

và

13
a.
4

 AB  SI
 AB   SIJ   AB  SH .

 AB  IJ
SH  AB
 SH   ABCD   SH   BDM  .
Do đó 
SH  IJ

 BM  SA
Gọi E  AH  BM . Ta có 
 BM  AH .
 BM  SH
Ta có ABE đồng dạng với AHI ( vì I  E  90 và A chung) nên ta có
AE AB

AB. AI
2a

 AE 

.
AI AH
AH
13
Ta có ABE đồng dạng với BMC ( vì C  E  90 và B  M ) nên ta có
AB AE
AB.BC
13a

.
 BM 

BM BC
AE
2

1 3a 1
a2
SBMD  SBMC  SBDC  .a .  .a.a 
2
2 2
4
1
1 3 1 2
3 3

Thể tích V của khối chóp S.BDM là V  .SH .S BMD  .
a. a 
a .
3
3 4 4
48

Câu 19: [2H1-2-4] (Toán Học Tuổi Trẻ - Tháng 12 - 2017) Xét khối tứ diện ABCD có
cạnh AB  2 3 và các cạnh còn lại đều bằng x . Tìm x để thể tích khối tứ diện

ABCD bằng 2 2 .
A. x  6 .
x  2 3.

B. x  2 2 .
Lời giải

Chọn B

C. x  3 2 .

D.


Gọi M là trung điểm của CD và H là hình chiếu của A trên BM .
CD  AM ; CD  BM  CD   ABM   AH   BCD  .

Đặt AMB   suy ra sin  
VABCD 

AH
x 3
.
 AH  sin  .
AM
2

1
512
1
x 3 x2 3
AH .S BCD  sin 
.
 2 2  sin 2   6 .
3
x
3
2
4

Xét tam giác AMB ta có: cos  

AM 2  BM 2  AB 2
8
 1 2 .
2 AM .BM
x
2

512 

8 
Ta được phương trình: 6  1  2   1 . Giả PT ta được x  2 2 .
x
 x 
Câu 20: [2H1-2-4] (Toán Học Tuổi Trẻ - Tháng 12 - 2017) Cho tứ diện đều ABCD có
cạnh bằng a . Gọi M , N lần lượt là trọng tâm của các tam giác ABD , ABC và
E là điểm đối xứng với B qua điểm D . Mặt phẳng  MNE  chia khối tứ diện

ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V .
Tính V .
a3 2
A.
.
96
9a 3 2
.
320

3a 3 2
C.
.
320

3a 3 2
B.
.
80

Lời giải
Chọn D

D.


Thể tích khối tứ diện đều cạnh a là:

a3 2
.
12

Gọi P  ME  AD ; T  ME  AB . Trong mặt phẳng  ABC  đường thẳng TN cắt AC ,

BC lần lượt tại Q , F . Khi đó mặt phẳng  MNE  chia khối tứ diện đã cho phần chứa đỉnh
A là tứ diện ATPQ .
Gọi I là trung điểm BD . Xét AID ta có:

ED MI PA
PA
.
.
3
 1 (định lý Menelaus) 
EI MA PD
PD

.
QA
3
QC

Tương tự ta có:
Xét AIB ta có:

Mặt khác ta có:

EI TB MA
TB 2
. .
 .
1 
EB TA MI
TA 3

VATPQ
VABCD

27 a3 2 9a3 2
AT AP AQ 3 3 3 27
.
 VATPQ  .


.
.
 . . 
80 12
320
AB AD AC 5 4 4 80

Câu 21: [2H1-2-4] (Toán Học Tuổi Trẻ - Tháng 12 - 2017) Trong tất cả các khối chóp

tứ giác đều ngoại tiếp mặt cầu bán kính bằng a , thể tích V của khối chóp có thể
tích nhỏ nhất.
8a 3
.
3
32a 3
V
.
3

A. V 

B. V 

10a 3
.
3

Lời giải
Chọn D

C. V  2a 3 .

D.


Giả sử SO  x ta có: SI  x  a ; SE 
Xét SEI ∽ SON ta có:

 x  a

2

 a 2  x 2  2ax

SE
IE
IE.SO

 NO 

SO NO
SE

ax
x 2  2ax

2

1  2ax 
4a 2 x 2
Thể tích khối chóp là: V  x. 


3  x 2  2ax  3  x  2a 
Xét hàm số f  x  

f  x 

x 2  4ax

 x  2a 

2

x2
x  2a

 0  2a  x 

; f   x   0  x  4a (do 0  2a  x )

Bảng biến thiên

Vậy giá trị nhỏ nhất của thể tích là: V 

32a 3
.
3

Câu 22: [2H1-2-4] (THPT Kinh Môn 2 - Hải Dương - 2018 - BTN) Cho hình chóp
S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SA , N là
điểm trên đoạn SB sao cho SN  2NB . Mặt phẳng  R  chứa MN cắt đoạn SD
tại Q và cắt đoạn SC tại P . Tỉ số

VS .MNPQ
VS . ABCD

lớn nhất bằng

A.

2
.
5

B.

1
.
3

C.

1
.
4

D.

3
.
8

Lời giải
Chọn D

Đặt

SM SP SN SQ
SQ 1
2
1 
SP
1




  x  x x  .
 x 0  x  1 . Ta có
SA SC SB SD
SC 2
3
6 
SC
6

Mặt khác ABCD là hình bình hành nên có VS . ABCD  2VS . ABC  2VS . ACD

VS .MNP SM SN SP 1 VS .MPQ SM SP SQ 1 
1

.
.
 x;

.
.

 x x   .
VS . ABC
SA SB SC 3
VS . ACD SA SC SD 2 
6
Suy ra

VS .MNPQ
VS . ABCD

Xét f  x  



V
VS .MNP
1
1 
1 1
1
 S .MPQ  x  x  x    x 2  x .
2VS . ABC 2VS . ACD 6
4 
6 4
8

1
1 2 1
1
1

1 1 
x  x với  x  1 ; f   x   x   0  x     ;1
6
4
8
2
8
4 6 

Bảng biến thiên:

Từ BBT ta có max f  x  
1 
 ;1
6 

VS .MNPQ
3
3
. Vậy
đạt giá trị lớn nhất bằng .
8
VS . ABCD
8


Câu 23: [2H1-2-4] (CỤM CÁC TRƯỜNG CHUYÊN ĐỒNG BẰNG SÔNG CỬU
LONG-LẦN 2-2018) Cho hình chóp S.ABC có AB  5 cm , BC  6 cm ,
CA  7 cm . Hình chiếu vuông góc của S xuống mặt phẳng  ABC  nằm bên trong
tam giác ABC . Các mặt phẳng  SAB  ,  SBC  ,  SCA  đều tạo với đáy một góc

60 . Gọi AD , BE , CF là các đường phân giác của tam giác ABC với D  BC ,
E  AC , F  AB . Thể tích S.DEF gần với số nào sau đây?
D. 3,4 cm3

C. 3,7 cm3

B. 4,1 cm3

A. 2,9 cm3

Lời giải
Chọn D
S

E

A
F
H

C

I

60°

D

B

Vì các mặt phẳng  SAB  ,  SBC  ,  SCA  đều tạo với đáy một góc 60 và hình
chiếu vuông góc của S xuống mặt phẳng  ABC  nằm bên trong tam giác ABC nên
ta có hình chiếu của S chính là tâm I của đường tròn nội tiếp tam giác ABC .
Gọi p là nửa chu vi tam giác ABC thì p 
Ta có : S ABC 

AB  BC  CA
9.
2

p  p  AB  p  BC  p  AC   6 6 và r 

Suy ra chiều cao của hình chóp là : h  r.tan 60  2 2
A

E
F
I

B

C
D

S 2 6
.

p
3