LÝ THUYẾT MŨ - LÔGARIT

Chuyên đề 5:
PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG CÓ CHỨA MŨ VÀ LOGARÍT
TÓM TẮT GIÁO KHOA
I. KIẾN THỨC CƠ BẢN VỀ HÀM SỐ MŨ
1. Các đònh nghóa:
•
n
n thua so
a a.a...a=
123

(n Z ,n 1,a R)
+
∈ ≥ ∈
•
1
a a=

a∀
•
0
a 1=

a 0∀ ≠
•
n
n
1
a
a
−

=

{ }
(n Z ,n 1,a R/ 0 )
+
∈ ≥ ∈

•
m
n
m
n
a a=
(
a 0;m,n N> ∈
)
•
m
n
m
n
m
n
1 1
a
a
a
−
= =
2. Các tính chất :

•
m n m n
a .a a
+
=
•
m
m n
n
a
a
a
−
=
•
m n n m m.n
(a ) (a ) a= =
•
n n n
(a.b) a .b=
•
n
n
n
a a
( )
b
b
=
3. Hàm số mũ: Dạng :

x
y a=
( a > 0 , a
≠
1 )
• Tập xác đònh :
D R=
• Tập giá trò :
T R
+
=
(
x
a 0 x R> ∀ ∈
)
• Tính đơn điệu:
* a > 1 :
x
y a=
đồng biến trên
R
* 0 < a < 1 :
x
y a=
nghòch biến trên
R

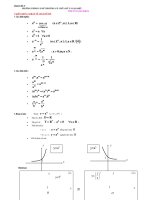
• Đồ thò hàm số mũ :
Minh họa:
20

a>1
y=a
x
y
x
1
0<a<1
y=a
x
y
x
1
f(x)=2^x
-4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 3.5 4 4.5
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0.5
1
1.5
2
2.5
3
3.5
x
y

f(x)=(1/2)^x
-4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 3.5 4 4.5
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0.5
1
1.5
2
2.5
3
3.5
x
y
y=2
x
y=
1
x
y
y
x
1
O
O
I. KIẾN THỨC CƠ BẢN VỀ HÀM SỐ LÔGARÍT

1. Đònh nghóa: Với a > 0 , a
≠
1 và N > 0

dn
M
a
log N M a N= ⇔ =


Điều kiện có nghóa :
N
a
log
có nghóa khi





>
≠
>
0
1
0
N
a
a

2. Các tính chất :
•
a
log 1 0=
•
a
log a 1=
•
M
a
log a M=
•
log N
a
a N=
•
a 1 2 a 1 a 2
log (N .N ) log N log N= +
•
1
a a 1 a 2
2
N
log ( ) log N log N
N
= −
•
a a
log N .log N
α

= α
Đặc biệt :
2
a a
log N 2.log N=
3. Công thức đổi cơ số :
•
a a b
log N log b.log N=
•
a
b
a
log N
log N
log b
=
* Hệ quả:
•
a
b
1
log b
log a
=
và
k a
a
1
log N log N

k
=

* Công thức đặc biệt:
a
b
c
c
b
a
loglog
=

4. Hàm số logarít: Dạng
a
y log x=
( a > 0 , a
≠
1 )
• Tập xác đònh :
+
=D R
• Tập giá trò
=T R
• Tính đơn điệu:
* a > 1 :
a
y log x=
đồng biến trên
+

R
* 0 < a < 1 :
a
y log x=
nghòch biến trên
+
R
• Đồ thò của hàm số lôgarít:

Minh họa:
5. CÁC ĐỊNH LÝ CƠ BẢN:
1. Đònh lý 1: Với 0 < a ≠ 1 thì : a
M
= a
N

⇔

M = N
2. Đònh lý 2: Với 0 < a <1 thì : a
M
< a
N

⇔
M
> N (nghòch biến)
21
0<a<1
y=log

a
x
1
x
y
O
f(x) =ln(x)/ ln(1/2 )
-4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 3.5 4 4.5
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0.5
1
1.5
2
2.5
3
3.5
x
y
y=log
2
x
x
y
x

y
f(x)=ln(x)/ln(2)
-4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 3.5 4 4.5
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0.5
1
1.5
2
2.5
3
3.5
x
y
xy
2
1
log=
1
O
1
O
a>1
y=log
a

x
1
y
x
O
3. Đònh lý 3: Với a > 1 thì : a
M
< a
N

⇔
M
< N (đồng biến )
4. Đònh lý 4: Với 0 < a
≠
1 và M > 0;N > 0 thì : log
a
M = log
a

N
⇔
M = N
5. Đònh lý 5: Với 0 < a <1 thì : log
a
M < log
a
N
⇔
M

>N (nghòch biến)
6. Đònh lý 6: Với a > 1 thì : log
a
M < log
a
N
⇔
M
< N (đồng biến)
III. CÁC PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH MŨ THƯỜNG SỬ DỤNG:
1. Phương pháp 1: Biến đổi phương trình về dạng cơ bản : a
M
= a
N

Ví dụ : Giải các phương trình sau :

x 10 x 5
x 10 x 15
16 0,125.8
+ +
− −
=


2. Phương pháp 2: Đặt ẩn phụ chuyển về phương trình đại số
Ví dụ : Giải các phương trình sau :
1)
2x 8 x 5
3 4.3 27 0

+ +
− + =

2)
x x x
6.9 13.6 6.4 0− + =

3)
x x
( 2 3 ) ( 2 3 ) 4− + + =
4)
322
2
2
2
=−
−+−
xxxx

5)
027.21812.48.3
=−−+
xxxx

6)
07.714.92.2
22
=+−
xxx

3. Phương pháp 3: Biến đổi phương trình về dạng tích số A.B = 0 ...
Ví dụ : Giải phương trình sau :
1) 8.3
x
+ 3.2
x
= 24 + 6
x

2)
0422.42
2
22
=+−−
−+
xxxxx



3)
20515.33.12
1
=−+
+
xxx
(
4. Phương pháp 4: Nhẩm nghiệm và sử dụng tính đơn điệu để chứng
minh nghiệm duy nhất (thường là sử dụng công cụ
đạo hàm)
* Ta thường sử dụng các tính chất sau:

• Tính chất 1 : Nếu hàm số f tăng ( hoặc giảm ) trong khỏang (a;b) thì phương trình f(x) = C có không quá một nghiệm trong khỏang (a;b).
( do đó nếu tồn tại x
0

∈
(a;b) sao cho
f(x
0
) = C thì đó là nghiệm duy nhất của phương trình f(x) = C)
• Tính chất 2 : Nếu hàm f tăng trong khỏang (a;b) và hàm g là hàm một hàm giảm trong khỏang (a;b) thì phương trình f(x) = g(x) có
nhiều nhất một nghiệm trong khỏang (a;b) . ( do đó nếu tồn tại x
0

∈
(a;b) sao cho f(x
0
) = g(x
0
) thì đó là nghiệm duy nhất của phương
trình f(x) = g(x))
Ví dụ : Giải các phương trình sau :
1) 3
x
+ 4
x
= 5
x
2) 2
x
= 1+

x
2
3
3)
x
1
( ) 2x 1
3
= +

IV. CÁC PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH LOGARIT THƯỜNG SỬ DỤNG:
1. Phương pháp 1: Biến đổi phương trình về dạng cơ bản :
a a
log M log N=

Ví dụ : Giải các phương trình sau :
1)
+ =
x
log (x 6) 3
2)
x x 1
log (4 4) x log (2 3)
2 1
2
+
+ = − −
3)
)3(log)4(log)1(log
2

1
2
2
1
2
2
xxx
−=++−
)
2. Phương pháp 2: Đặt ẩn phụ chuyển về phương trình đại số.
Ví dụ : Giải các phương trình sau :
1)
3
3
2 2
4
log x log x
3
+ =
2)
051loglog
2
3
2
3
=−++
xx

3. Phương pháp 3: Biến đổi phương trình về dạng tích số A.B = 0 ...
Ví dụ : Giải phương trình sau :

2 7 2 7
log x 2.log x 2 log x.log x+ = +

4. Phương pháp 4: Nhẩm nghiệm và sử dụng tính đơn điệu để chứng minh
nghiệm duy nhất.
(thường là sử dụng công cụ đạo hàm)
22
* Ta thường sử dụng các tính chất sau:
• Tính chất 1 : Nếu hàm số f tăng ( hoặc giảm ) trong khỏang (a;b) thì phương trình f(x) = C có không quá một nghiệm trong khỏang (a;b).
( do đó nếu tồn tại x
0

∈
(a;b) sao cho
f(x
0
) = C thì đó là nghiệm duy nhất của phương trình f(x) = C)
• Tính chất 2 : Nếu hàm f tăng trong khỏang (a;b) và hàm g là hàm một hàm giảm trong khỏang (a;b) thì phương trình f(x) = g(x) có
nhiều nhất một nghiệm trong khỏang (a;b) . ( do đó nếu tồn tại x
0

∈
(a;b) sao cho f(x
0
) = g(x
0
) thì đó là nghiệm duy nhất của phương
trình f(x) = g(x))
Ví dụ : Giải các phương trình sau :

2
2 2
log (x x 6) x log (x 2) 4− − + = + +

V. CÁC PHƯƠNG PHÁP GIẢI BẤT PHƯƠNG TRÌNH MŨ THƯỜNG SỬ DỤNG:
1. Phương pháp 1: Biến đổi phương trình về dạng cơ bản : a
M
< a
N
(
, ,
≤ > ≥
)
Ví dụ : Giải các bất phương trình sau :
1)
2
x x 1
x 2x
1
3 ( )
3
− −
−
≥

2)
2
x 1
x 2x

1
2
2
−
−
≥

2. Phương pháp 2: Đặt ẩn phụ chuyển về bất phương trình đại số.
Ví dụ : Giải các phương trình sau :
1)
2x x 2
2 3.(2 ) 32 0
+
− + <
4)
52428
11
>+−+
++
xxx
2)
x 3 x
2 2 9
−
+ ≤
5)
11
21212.15
++
+−≥+

xxx

3)
2 1
1
x x
1 1
( ) 3.( ) 12
3 3
+
+ >
6)
0449.314.2
≥−+
xxx


VI. CÁC PHƯƠNG PHÁP GIẢI BẤT PHƯƠNG TRÌNH LOGARIT THƯỜNG SỬ
DỤNG:
1. Phương pháp 1: Biến đổi phương trình về dạng cơ bản :
a a
log M log N<

(
, ,≤ > ≥
)
Ví dụ : Giải các bất phương trình sau :
1)
2
x

log (5x 8x 3) 2− + >
2)
− <
2 3
3
log log x 3 1

3)
2
3x x
log (3 x) 1
−
− >
4)
x
x 9
log (log (3 9)) 1− ≤


5)
)12(log12log4)1444(log
2
555
++<−+
−
xx
2. Phương pháp 2: Đặt ẩn phụ chuyển về bất phương trình đại số.
Ví dụ : Giải các phương trình sau :
1)
x

x
2
3 2
log (3 2) 2.log 2 3 0
+
+ + − >

2)
2
2x
x
log 64 log 16 3+ ≥

23